无限大非接地导体平板的静电感应

付全红，郑建邦，樊元成，张富利

(西北工业大学 物理科学与技术学院, 物理实验教学中心，陕西 西安 710129)

导体与静电场的相互作用，即导体的静电感应，是大学物理电磁学部分的重要内容. 深刻理解导体的静电感应规律需要用到静电场边值问题的唯一性定理，但是该定理在大学物理中并未涉及，一般在物理类专业的专业基础课“电磁学”或“电动力学”中才会涉及，因此，导体的静电感应问题是大学物理教学中的一个难点. 在大学物理电磁学部分的教学中，通常以空腔导体和无限大导体平板的静电感应问题作为导体静电感应问题的教学案例. 空腔导体的静电感应问题相对简单，而无限大导体平板的静电感应问题相对复杂. 尽管无限大接地导体平板的静电感应问题是“电动力学”教材中利用电像法求解静电场边值问题的经典案例[1]，而且相关问题被广泛讨论[2-10]，但是无限大非接地导体平板的静电感应问题讨论较少[11]，而且缺乏严格的论证，甚至存在错误. 本文利用静电场边值问题的唯一性定理，严格分析无限大非接地导体平板的静电感应问题，利用COMSOL多物理场仿真软件对理论计算结果进行验证，以纠正对无限大非接地导体平板的静电感应问题的误解.

1 无限大接地导体平板的静电感应

在分析无限大非接地导体平板的静电感应问题之前，先回顾一下“电动力学”教材中无限大接地导体平板的静电感应问题. 如图1所示，有一个厚度为d无限大接地导体平板，在导体平板一侧距离为a处放置一个点电荷q，求空间的电场分布. 该问题是“电动力学”教材中利用电像法求解静电场边值问题的经典案例，其结果已为大家所熟知. 无限大导体平板将整个空间分为上、下两部分，假设上半空间(z>0) 的电势为φ1，下半空间(z<-d)的电势为φ2，则电势分布的定解问题为：

图1 无限大接地导体平板的静电感应

(1)

(2)

根据电像法，像电荷位于 (0, 0, -a) ，电荷量为-q，定解问题 (1) 的解为

(3)

(4)

(5)

导体平板上表面的感应电荷总量为

(6)

显然，定解问题 (2) 的解为

φ2=0

(7)

(8)

根据电场叠加原理，点电荷q和导体平板上表面的感应电荷σ0(x,y) 在导体平板中和下半空间，即z< 0区域，产生的电场强度之和为0.

2 无限大非接地导体平板的静电感应

若无限大导体平板未接地，如图2所示，则不能直接利用电像法来求解. 假设导体平板带电荷总量为Q，面积为S，电势为φx(Q和φx并不相互独立，若Q给定，则φx随之确定)，上半空间 (z> 0) 的电势为φ1，下半空间 (z< -d) 的电势为φ2(在本问题中，虽然电荷分布在无限大区域，但是由于不涉及具体的电势数值，所以仍然可以选择无穷远处为电势零点，并不会造成电势发散困难)，则电势分布的定解问题为

图2 无限大非接地导体平板的静电感应

(9)

(10)

(11)

(12)

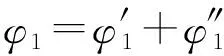
定解问题 (11) 与定解问题 (1) 相同，因此，它们的解也相同，即

(13)

定解问题 (12) 的解为

(14)

式中，b1和c1为待定常量.

因此，定解问题 (9) 的解为

(15)

(16)

(17)

导体平板上表面的感应电荷总量为

(18)

定解问题 (10) 的解为

φ2=b2z+c2

(19)

(20)

式中，b2和c2为待定常量.

σ下(x,y)=ε0b2

(21)

导体平板下表面的感应电荷总量为

(22)

b2=-b1

(23)

其值可由导体平板带电荷总量来确定.

导体平板带电荷总量为

(24)

因此

(25)

(26)

将式 (25) 和式(26)分别代入式 (16)—(18)和式(20)—(22) , 得

(27)

(28)

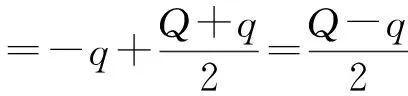
(29)

(30)

(31)

(32)

由此可见，无限大导体平板不接地时电场可以分为两部分，一部分是导体平板接地时的电场，即

(33)

E2,1=0

(34)

另一部分是将点电荷转移到导体平板时的电场，即

(35)

(36)

同样，无限大导体平板不接地时的电荷分布也可以分为两部分，一部分是导体平板接地时的电荷分布，即

(37)

Q上,1=-q

(38)

σ下,1(x,y)=0

(39)

Q下,1=0

(40)

另一部分是将点电荷转移到导体平板时的电荷分布，即

(41)

(42)

(43)

(44)

对于有限大小非接地导体平板，只要q和场点与导体平板的距离远小于导体平板的半径，则电场和电荷分布的第一部分与无限大导体平板的情形相同，即式(33)、(34)、(37)—(40)仍然成立，由式(37)可知，距离无限大导体平板的中心越远，电荷密度越小，在距离平板中心足够远的地方，感应电荷可以忽略；但是，电场和电荷分布的第二部分与无限大导体平板的情形差异较大，即式(35)、(36)、(41)、(43)不再成立，因为同种电荷相互排斥，电荷分布不均匀，距离有限大小导体平板的中心越远，电荷密度越大，平板中心附近的电荷密度小于平均电荷密度；根据对称性，E1,2和E2,2关于平板的中心面镜像对称，即切向分量相等，法向分量互为负矢量，式(42)、(44)、(29)、(32)仍然成立.

3 COMSOL仿真验证

为了证明上述分析和结果正确，我们利用COMSOL多物理场仿真软件分别从电场和电荷的角度对理论计算结果进行验证. 由于在COMSOL软件中，不能仿真无限大导体平板，所以我们只验证有限大小非接地导体平板的情形. 为了更加充分地表明理论计算结果的正确性，我们采用不同的模型参数(不同的Q)分别对电场分布和电荷进行验证，以避免出现“大数吃小数”的情况.

1) 验证电场分布

几何模型：点电荷用半径为0.01 mm的带电导体球代替；导体平板的厚度为1 mm，半径为1 000 mm；点电荷与导体平板的距离为100 mm；模型的外边界是半径为10 000 mm的球面.

边界条件：带电导体球的表面设置为悬浮电位，电荷量为q=1 C；导体平板的表面设置为悬浮电位，电荷量为Q=100 C；模型的外边界接地.

如前所述，对于有限大小非接地导体平板，只要q和场点与导体平板的距离远小于导体平板的半径，则E1,2和E2,2关于平板的中心面镜像对称. 因此，有限大小非接地导体平板上、下表面的电场之和为

(45)

图3(a)表明有限大小非接地导体平板上、下表面的电场之和的仿真与理论结果完全一致；图3(b)表明有限大小非接地导体平板下表面的电场分布不均匀，距离平板中心越远，电场强度越大，平板中心附近的电场强度小于平均电场强度，由导体表面的边值关系可知，这与前述的电荷分布规律一致.

图3 有限大小非接地导体平板的电场[(a) 上、下表面的电场之和;(b) 下表面的电场. 上表面z=0,y=0；下表面z=-1 mm,y=0]

2) 验证电荷

几何模型：点电荷用半径为0.01 mm的带电导体球代替；导体平板的厚度为1 mm，半径为1 000 mm；点电荷与导体平板的距离为100 mm；模型的外边界是半径为10 000 mm的球面.

边界条件：带电导体球的表面设置为悬浮电位，电荷量为q=1 C；导体平板的表面设置为悬浮电位，电荷量为Q=1 C；模型的外边界接地.

在COMSOL多物理场仿真软件中，对面电荷密度作面积分，可求得导体平板上、下表面的电荷总量分别为0.019 5 C和0.925 1 C(侧面电荷总量为0.035 4 C).

由式(29)和式(32)可知，导体平板上、下表面电荷总量的理论值分别为0和1 C. 在误差允许范围内，仿真结果与理论计算结果一致.

电场分布和电荷的COMSOL仿真结果都表明前述分析和结果正确.

4 结论

利用静电场边值问题的唯一性定理，严格分析了无限大非接地导体平板的静电感应问题.无限大导体平板不接地时的电场可以分为两部分，一部分是导体平板接地时的电场，另一部分是将点电荷转移到导体平板时的电场；同样，无限大导体平板不接地时的电荷分布也可以分为两部分，一部分是导体平板接地时的电荷分布，另一部分是将点电荷转移到导体平板时的电荷分布. COMSOL多物理场仿真结果与理论计算结果一致.