两串联弹簧等效质量的研究*——基于多普勒效应综合实验仪
何香林 刘竹琴
(延安大学物理与电子信息学院 陕西 延安 716000)
当弹簧可视为轻质弹簧时,满足胡克定律[1,2],但在研究实际弹簧振子的振动问题时,大多时候弹簧不可视为轻质弹簧,文献[3]详细阐述了有质量弹簧对振动的影响,也有大量文献研究了单弹簧的等效质量[4~6],这为本文提供了理论基础与思考方向.在实际工程应用中往往不只是有单弹簧与振子组成的振动系统,更多的是诸如两弹簧串联、两弹簧并联、多弹簧串联等分别与振子组成的复杂弹簧振子系统,复杂弹簧振子等效质量的确定仍有待研究.因为在竖直方向上弹簧质量对振动周期影响最大[7],实验效果最为明显,所以本文将对竖直方向上两串联弹簧的等效质量进行研究.研究结果为多弹簧串联等效质量的确定以及实际工程应用提供了实验基础,使学生了解到振动周期不仅与振子质量、弹簧劲度系数有关,还与弹簧自身质量、位置分布有关.
1 实验原理与实验装置
1.1 实验原理
1.1.1 周期的测量
多普勒效应综合实验仪可以设置采样步距、采样次数,并且能够采集弹簧振子振动的v-t图像.在简谐振动过程中,采集到的v-t图呈三角函数图像,方向相同且最大的相邻两个速度所对应的采样次数之差乘以采样步距的值等于周期.为方便计算以及减小实验误差,采样步距设置为0.1 s,采样次数设置为最多次数150次,第b次(即最后一次)与第1次速度最大且方向相同的采样次数之差设为Nb-N1,则周期的计算满足式(1),即
(1)
1.1.2 等效质量的测量
在研究有质量弹簧与振子所组成的振动系统的运动规律时,周期计算公式如式(2)[8],T,κ,m0,m分别为振动周期、弹簧劲度系数、振子质量、弹簧等效质量,两边平方整理得式(3).在此实验中,收集多组振子质量和与之对应的周期平方的值,作T2-m0的二元一次函数图,设其斜率为a、截距为d,联立式(3)、(4)便可求出等效质量的测量值.
(2)
(3)
(4)
1.2 实验装置
实验装置由红外接收器、自由落体组件、底座及发生器、电磁阀、保护盒、砝码、电子秤、质量分别为5.8 g与11.0g的两弹簧及导轨组成.当两弹簧串联时,挂上振子后弹簧伸长量过大,为得到足够的实验数据以达到减小实验误差的目的,需将两导轨串接,此时需放置保护盒,如图1所示.
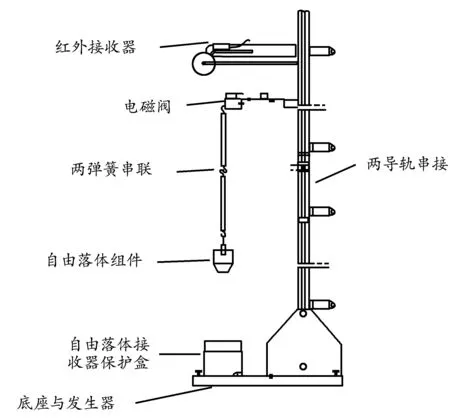
图1 测量两串联弹簧等效质量的实验装置图
2 实验方法与测量举例
2.1 实验方法
(1)令质量为5.8 g的弹簧为弹簧1,11.0 g的弹簧为弹簧2,当两弹簧串联后,弹簧1在固定端,即弹簧1悬挂于电磁阀上方的挂钩孔中,振子悬挂于弹簧2一端,实验步骤如下:
1)设置好多普勒效应综合实验仪的相关参数,将电子秤称量好的振子质量记录于表1,适当下拉振子使系统做简谐运动,待其稳定后,开始采集v-t图像.
2)为减小实验误差,多次采集v-t图像,多次记录第一次与最后一次速度最大且方向相同采样次数的差,并取平均值,利用式(1)可得周期,再平方即可得出周期平方的值并记录于表中.
3)改变振子质量,重复上述步骤,共收集6组振子质量和与之对应的周期平方的值.
4)在Excel中输入6组数据,得二元一次方程,并作出T2-m0函数图像,联立式(3)、(4)求出等效质量的测量值.
5)利用函数图像以及测量值,研究等效质量与两单弹簧自身质量、劲度系数的关系.
(2)当弹簧2在固定端时,步骤同上,并比较两次的测量值是否一致.
2.2 测量举例
2.2.1 数据记录
(1)振子质量分别为101.0 g,118.0 g,134.0 g,145.9 g,167.9 g,178.1 g,周期平方取小数点后4位.弹簧1悬挂于固定端时,所得数据如表1所示.
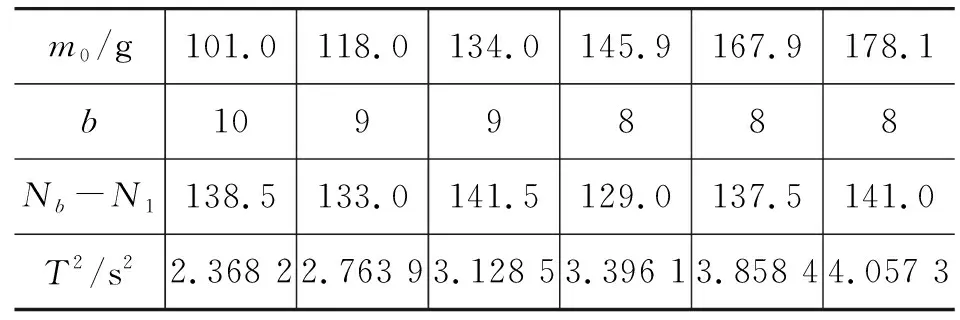
表1 弹簧1悬挂于固定端时的数据记录表
(2)弹簧2悬挂于固定端时,所得数据如表2所示.
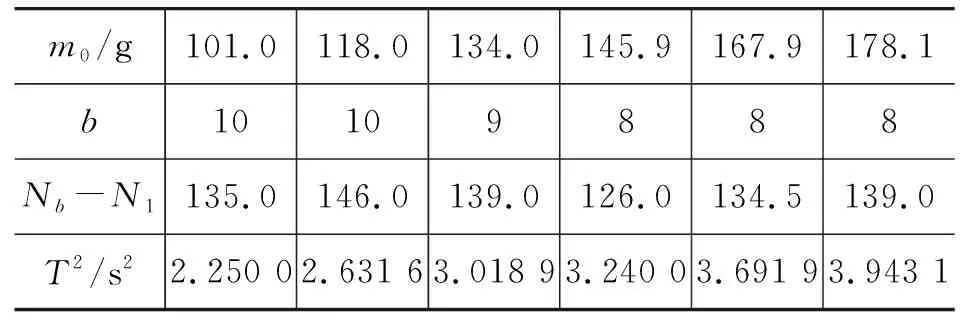
表2 弹簧2悬挂于固定端时的数据记录表
2.2.2 数据处理
(1)弹簧1悬挂于固定端所对应的线性回归曲线,如图2所示,其相关系数R2为0.999 2,趋近于1,趋势线精确度较高.
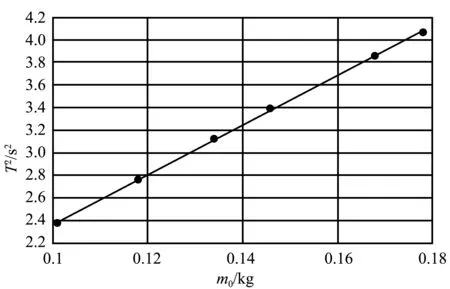
图2 弹簧1悬挂于固定端的T2-m0函数曲线图
图2所对应的线性回归方程为
T2=21.937m0+0.172 6
(5)
此时a为21.937,d为0.172 6,代入式(4),保留小数点后4位,解得弹簧等效质量的测量值为7.868 0 g.
经测量,弹簧1的劲度系数为3.087 1,弹簧2的劲度系数为4.561 0,测量方法与等效质量测量方法类似,不同之处便是只需知道T2-m0函数图像的斜率即可求出劲度系数,这里不再赘述.设等效质量与两单弹簧自身质量的关系如式(6),c1与η满足的函数关系如式(7),c2与η满足的函数关系如式(8),η为悬挂振子端与固定端弹簧劲度系数的比值[9].m1,κ1,c1分别为固定端弹簧的质量、劲度系数、相关系数,m2,κ2,c2为悬挂振子端弹簧的质量、劲度系数、相关系数.
m=c1m1+c2m2
(6)
(7)
(8)
(9)
联立式(6)~(9)解出此时等效质量的理论值为7.844 9 g,约等于测量值.理论值与测量值的百分误差为0.29%,在误差范围内,则假设成立.
(2)弹簧2悬挂于固定端所对应的线性回归曲线,如图3所示.其相关系数R2为0.998 9,趋近于1,趋势线精确度较高.
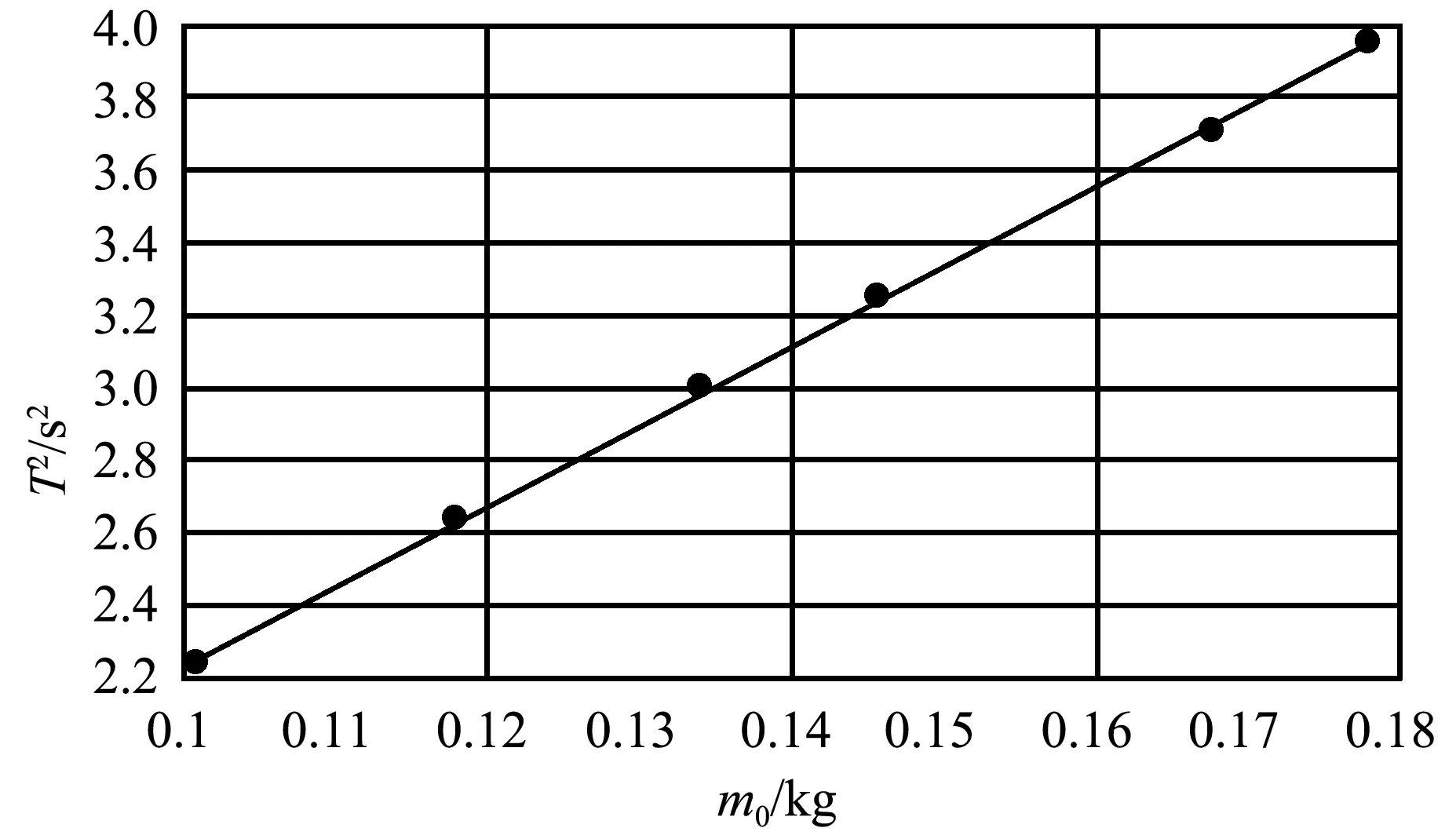
图3 弹簧2悬挂于固定端的T2-m0函数曲线
图3所对应的线性回归方程为
T2=21.679m0+0.076 5
(10)
此时a为21.679,d为0.076 5,代入式(4),保留小数点后4位,解得弹簧等效质量的测量值为3.528 8 g,与弹簧1悬挂于固定端所得等效质量的值不一致.
联立式(6)~(9)解出此时等效质量的理论值为3.626 1 g,约等于测量值.理论值与测量值的百分误差为2.68%,在误差范围内,则假设成立.
综上可知:
(1)竖直方向两串联弹簧的等效质量与弹簧的位置分布有关;
(2)等效质量的大小与单弹簧自身质量、劲度系数满足关系式(6)~(9).
3 结束语
本文设计了基于多普勒效应综合实验仪研究两串联弹簧等效质量的方案,并将标准值与测量值进行了比较,实验误差分别为0.29%和2.68%,结果精确度较高.但本文在最初收集、处理实验数据过程中得出的百分误差较大,在多次收集、处理实验数据后,才最终得出误差较小的等效质量的测量值.究其原因:
(1)与研究等效劲度系数不同的是,研究等效质量所要求的精确度更高;
(2)采用质量较轻的弹簧,函数图像斜率与截距的微小变化都会严重影响到等效质量的测量值与理论值的百分误差.
通过本次实验,可以提高学生的创新意识、竞争与合作意识、科技意识,以及培养学生批判、严谨认真、实事求是的科学态度.

