基于边坡稳定分析方法的进展探究

王 毅 李中尧 史海平 王培清

（西藏农牧学院， 西藏 林芝 860000）

本文重点对实际工作中常用的一般研究分析法来展开探究，进而推动其相关研究的进程，为其提供更加合理化、科学化的学术依据。就现阶段来看，常用的分析法主要是以极限平衡法、有限单元法、强度折减法以及一些定性分析法为主，针对其确定性与不确定性相关稳定性分析法。由此可见，面对多元化的方式方法，了解其每一项特点与作用，进而才能够在实际工作当中进行合理的应用，使其作用得到充分发挥。

1 不确定性分析法

1.1 人工神经网络分析法

人工神经网络分析法是通过神经网络学习和联想记忆功能，来把边坡稳定分析与治理情况进行汇总，通过信息化技术的应用进而能够形成一种网络数据库。不过此分析法仍在不断研究中，还有很多方面需要完善，其体系还需要进一步健全，因而在实际工作当中的实用性不强，不过其优良的非线性表示能力与优质学习能力比较突出，在未来或许会成为推动边坡稳定分析研究变革的关键因素。

1.2 灰色系统分析法

灰色系统分析法是将灰色系统能够将边坡看作为一个完整系统，并通过灰色模糊集理论对其进行分析，将系统中未知部分进行灰色关联、建模与预测，从而能够对整个边坡的信息数据进行管控，并且还能够根据其不确定性因素从而衡量因素间关联程序，进而实现对其稳定性的分析。

1.3 模糊分析法

模糊分析法是将模糊理论融入到边坡稳定性分析中，从而能够通过函数的方式来获取影响边坡稳定性的相关因素，其特点就是在于应用的范围，比较适用于一些边界不清且有多变量影响因素中，最大的缺点就是函数的确定与因素权重分配较为主观性，因而应用较少，还是要根据实际情况，符合其应用相关条件，才会使用这种分析法[1]。

2 确定性分析法

2.1 有限单元法

有限单元法的核心理念就是把岩体看作连续力学介质，并采取离散化方式，进而构建起近似函数，将有界区域中无限问题简化为有限问题，进而对边坡内部结构性质进行编写，实现应力与变形分析。这种方法能够对边坡受力破坏进行过程模拟，进而体现出其适用性特点，全面剖析边坡变形破坏机理，并掌握其变形破坏规律，通过计算的方式，可得出滑动面应力，这种分析法虽然结果更加精确，不过缺陷就是在于数据准备工作量大，且整个计算效率偏低。现阶段，在实际的工作当中，应用最为广泛的就是有限元强度折减法和有限元重度增加法以及有限元圆弧搜索法[2]。

2.2 权限平衡法

极限平衡法的原理主要指按照静力平衡关系进行分析，应用在边坡稳定分析中就是，通过力学模型进行展现，在计算方面也比较简便，且容易处理工程中复杂的土层剖面和外部荷载问题，同时，还能够定量对边坡稳定性进行分析与评价。目前，关于这种方法的应用越来越成熟，也是应用最广泛的一种，特别是在近几年中，得到了大力地推广，已经成为边坡稳定分析方法中作用和优势最明显的一种。不过这一方法与其他方法一样，也有一定的缺陷存在，主要就是局限性。比如说，在实际应用当中，使用这种分析法时，若没有对岩土体应力和应变之间的关系作进一步了解，而只关注土体破坏瞬间变形机制，则不能够获取更加精确的边坡破坏发生与发展过程分析结果，同时，还需提前了解滑动面位置与形状这些因素，由此可见任何一种方法的应用都一定要充分考虑到应该注重的事项，进而才能够使其作用得到发挥。就目前的形势来看，三维极限平衡法发展越来越好，其理论模型分别为三维简化简布法、三维普通条分法、三维斯宾塞法等等，都是以二维极限平衡法为基础而形成[3]。

这种方法的计算效果良好，例如：根据统一公式中非严格条分法计算安全系数的正确性某边坡，容重 =30kN/m3，粘结力 =40kPa，内摩擦角=18°，坡高 =20m，坡角 =30°，圆心座标Xc=68.138m，Yc=10.245m，圆弧深度3=30.525m，土条分成20 块的圆弧滑移面用统一公式及土质边坡稳定分析，其安全系数值见表1。

表1 计算结果

2.3 边界单元法

边界单元法与有限单元法有很大区别，并不是把边坡整体进行划分，则是对其边界区域危险滑坡体划分，采取构建边界积分方程与线性方程的方式进而求解边界处单元体应力与位移，最终以计算边坡稳定安全系数为主。这种方法也有一定的局限性，就是由于性能不够全面需要根据实际特殊情况才能进行应用，一般来说，在非均质和非线性边坡问题方面，都不适用于这种分析法。

2.4 离散单元法

离散的含义就是把边坡离散成多个块体单元，进而通过单元间接触关系创设出力和位移之间的联系，并根据迭代求解动力平衡方程进行求解，进而能够精确的得出岩块间接触面滑移数据信息，同时，还能对分离和倾翻大位移以及岩块内部变形和应力分布进行求解。这种方法的缺点就是不能够实际模拟岩体裂缝产生和失稳过程，致使部分参数过于盲目[4]。

3 定性分析法

3.1 工程类比法

工程类比法主要应用于工程地质条件复杂且缺乏详细资料的边坡稳定性分析，该方法通过全面分析、对比研究边坡与已有边坡间可能存在的相似点和差别点，把已有边坡的稳定性状况及其影响因素等方面的经验应用到类似边坡的稳定性分析和设计中，从而分析和判断研究对象的稳定性状况、发展趋势和加固处理设计等。

3.2 图解法

图解法有两种类型，一种是诺模图法，另一种则是赤平极射投影法。第一种比较适合应用在圆弧形潜在破坏面土质类边坡稳定分析中，通过诺模图进而展现出边坡稳定性参数间影响的关系，进而得出其安全系数，以此为依据来对其稳定性进行评价[5]。而第二种则是在于探究岩质边坡稳定性分析，根据赤平极射投影的根本理念，能够制定出边坡破坏边界与其结构的空间关系图，进而能够通过分析边坡形态与存在的危险因素和滑动面方向，对其稳定性进行评价。这两种方法科学性较强，因而得出的结果准确性能够得到有效保障。

4 双强度折减法

双强度折减法如今的研究已基本定型，对于其应用已有很多实际案例以及学术文献作为参考，但要想能够使其在边坡稳定性分析中作用得到更好的发挥，就需要对其进一步改善，在实际折减过程中，可在黏聚力与内摩擦角间折减系数取不同值，计算如下：

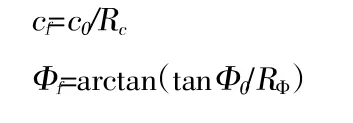
5 结束语

此次研究重点是基于边坡稳定分析方法的进展展开研究，通过对不同分析方法的解析和探究，对其进行回顾，进而体现出不同方法中的特点与缺点所在，以此来为边坡稳定相关的研究提供更多的事实依据。通过对当下存在的各类分析法进行分析，体现出未来边坡稳定分析发展趋势，为此类研究的开展提供有效保障。本次研究具备一定的技术性，主要就是以探究各类科学性、技术型的分析方法为主，从中发现了每一种方法的优点与缺点。总的来说，具体方法的应用还是要根据分析边坡稳定的实际情况来进行选择，才能够确保相关研究顺利进行。本文通过对双强度折减法研究发现其对于边坡稳定性分析中存在较多参数影响，虽然已有相关部门和专家学者们提出了解决问题的方法，但是在方法统一方面仍然有对立观点存在，关于边坡稳定分析还需相关部门和专家学者们不断的努力，持续研究，进而才能够使其得到进一步的发展。