半正型四阶脉冲微分方程边值问题的正解

彭 皓，柏仕坤

重庆师范大学数学科学学院，重庆，401331

众所周知，自然界中有许多现象在发展过程中会出现短时间内的扰动，这类扰动能瞬时地改变系统状态，其影响往往是不可忽略的。基于此，常微分方程的脉冲效应自然能引发人们的广泛关注[1-9]。例如，刘立山等[1]运用不动点指数研究以下的二阶脉冲微分方程组两点边值问题正解的存在性：

其中J′=(0,1){t1,t2,…,tm},fi≥0,i=1,2。文献[2]中作者运用类似于[1]的方法研究了一个高阶脉冲微分方程积分边值问题正解的存在性：

受上述文献的启发，在半正型非线性项和脉冲项的条件下，讨论如下四阶脉冲微分方程边值问题：

(1)

正解的存在性，f,Ik在无穷远处满足一定的增长性条件。其中ti∈(0,1),且

分别是y′在t=tk点处的右极限和左极限。非线性f和脉冲项Ik满足以下条件：

(H0)f∈C([0,1]×R+,R),Ik∈C(R+,R),且存在正数M,Mk(k=1,2,…,m)使得

f(t,y)≥-M,Ik(y(tk))≥-Mk,∀t∈[0,1],y∈R+,k=1,2,…,m。

1 预备知识

令E=C[0,1],‖y‖=supt∈[0,1]|y(t)|,则(E,‖·‖)是一实Banach空间。鉴于脉冲效应的出现，亦需要以下的空间

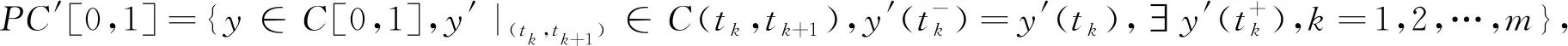
引理1[3]四阶脉冲微分方程边值问题(1)等价于如下的积分方程

(2)

其中

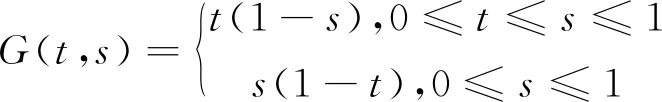
(3)

引理2Green函数G满足以下一些性质：

(1)G∈C([0,1]×[0,1],R+),G(t,s)>0,∀t,s∈(0,1);

(2)t(1-t)s(1-s)≤G(t,s)≤s(1-s),∀t,s∈[0,1];

(3)G(t,s)≤t(1-t),∀t,s∈[0,1];

这四种性质直接由G的定义可得，故略去它们的证明。

为了证明本文的定理，先给出两个引理[10]：

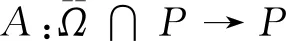
y-Ay≠λy0,∀y∈∂Ω∩P,λ≥0,

则i(A,Ω∩P,P)=0,其中i是锥P上的不动点指数。

y≠λAy,∀y∈∂Ω∩P,λ∈[0,1],则i(A,Ω∩P,P)=1。

2 主要结论

由于非线性项f和脉冲项Ik可变号，为了方便研究,将构造如下非负算子方程。为此，需要考虑以下四阶脉冲微分方程边值问题：

(4)

根据引理1知(4)的解可以表示为：

(5)

定理1若y*是(1)的正解，则y*+ω是如下方程的解：

(6)

其中

(7)

反过来，若y*是(6)的解，且y*(t)≥ω(t),∀t∈[0,1],则y*-ω是(1)的正解。

证明：已知(1)与(2)等价，所以当y*是(1)的正解时，y*满足以下方程：

(8)

运用(7)可得:

从而

此即证明了y*+ω是(6)的解。

反过来，将y*代入(6)可得:

注意到y*(t)≥ω(t),∀t∈[0,1],则

此即

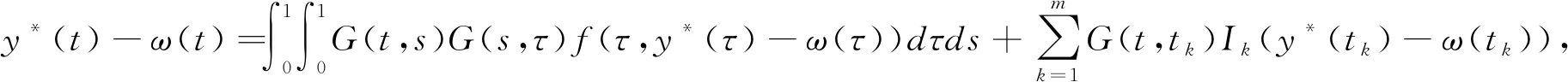
定理1表明,可以通过研究方程(6)超过ω的解，即可获得(1)的正解。定义算子

则根据前面的讨论知(6)解的存在性等价于算子A不动点的存在性。定义集合

P={y∈E:y(t)≥t(1-t)‖y‖,∀t∈[0,1]},则有以下的结论。

定理2A(P)⊂P,且当y∈P,‖y‖≥时，y(t)≥ω(t),∀t∈[0,1],其中

证明:根据算子A的定义和引理1(ii)易证A(P)⊂P。 由引理1(iii)知当y∈P时有

为了得到解的存在性定理，这里先给出所要使用的假设条件:

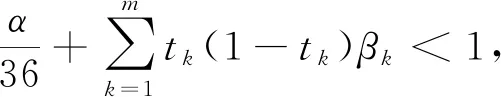
f(t,y)+M≤αy,Ik(y)+Mk≤βky,∀t∈[0,1],y∈[0,],k=1,2,…,m。

定理3如果(H0)-(H2)成立，则(1)至少有一个正解。

证明:令Bρ={y∈E:‖y‖<ρ},ρ>0。先证

y≠λAy,λ∈[0,1],y∈∂B∩P

(9)

事实上，若上式不成立，则存在y0∈∂B∩P,λ0∈[0,1]使得

y0(t)=λ0(Ay)(t),∀t∈[0,1]

(10)

此即表明

‖y0‖≤‖Ay0‖

(11)

另一方面，由(10)知y0∈P,且‖y0‖=,从而y0≥ω。 根据(H1)有

此即表明

‖Ay0‖<‖y0‖,y0∈∂B∩P

(12)

这与(11)矛盾，从而(9)成立，根据引理4得

i(A,B∩P,P)=1

(13)

最后证明

(14)

其中R>是一正常数,是一固定元素。若上式不成立，则存在y1∈∂BR∩P,λ1≥0使得

(15)

根据定理2知y1∈P。 另外注意到

从而存在d,dk>0使得

f(t,y)+M≥γy-d,Ik(y)+Mk≥δky-dk,∀t∈[0,1],y∈R+,k=1,2,…,m.

则根据(15)可得

在上式两端乘以sinπt,并在[0,1]上积分经整理可得

根据引理2(iv)可得

注意到y1∈P,从而

‖y1‖≤

‖y1‖：=Θ1

(16)

由(15)和(16)知：若R>max{,Θ1},则(14)成立。从而根据引理3可得

i(A,BR∩P,P)=0.

(17)

至此，根据(13)和(17)可得

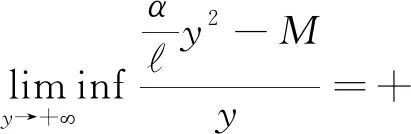
从而f,Ik(k=1,2,…,m)满足(H0)-(H2)。

3 结 语

本文运用不动点指数理论给出了问题(1)正解的存在性，且f,Ik可变号(下方有界)，这是数学模型中的半正问题。该模型源于现实生活中诸多实际问题，所以对这些问题的研究不仅加深人们对数学相关理论的认识，而且也有助于增强人们对相关自然现象的理解和驾驭能力。毫无疑问，对变号非线性微分方程的研究既有重要的理论意义，又有广泛的现实背景和应用价值。