县域尺度下不同时序茶园景观格局指数的粒度效应分析
马黛玉,夏建国*,周玥希,黄子健,肖欣娟
(1.四川农业大学资源学院,成都 611130;2.成都市农业技术推广总站,成都 610041)
在景观生态学中,尺度指空间粒度和幅度。尺度的合理性如何是决定研究区景观格局的分析是否具有科学性的关键,也是近年来景观生态学和地理学研究的重点问题之一[1]。空间粒度是景观中最小可辨别单元所代表的长度、面积或体积,随着最小可辨别单元的改变,分析结果也随之改变[2]。景观指数具有强烈的尺度依赖性,在研究过程中,当研究对象的空间幅度和时间幅度一定时,景观格局指数受粒度变化的影响[3]。同一景观由于研究地区、研究幅度或研究时限不同,其景观格局指数的粒度效应也存在差异[4-5]。因此,不存在所有景观格局分析的最佳尺度,只有针对特定景观的适宜尺度[6]。如:崔杨林等[7]通过像元尺度上推改变空间粒度,发现耕地适宜粒度域为100~130 m,林地适宜粒度域为100~110 m,县域整体景观格局最佳粒度为100 m;翟俊等[8]认为青海流域景观格局分析的最佳空间粒度为90 m;吴未等[9]以土地利用类型、热力等级和生态贡献为斑块类型划分依据构建3种不同景观格局,发现无锡市景观格局适宜研究尺度为60~210 m。
当前,多数学者针对土地利用景观格局的尺度效应研究主要集中在不同空间尺度对景观指数的影响方面[10-12]。这些研究虽然分析了不同区域土地利用景观格局分析时最适宜的尺度域,但多数研究着眼于某一时点上的[4,12-13]土地利用景观的静态空间尺度效应分析,缺乏针对不同时点的动态分析,且主要强调土地利用整体景观,有部分研究针对居民点[6,14]、耕地[15-16]景观格局的研究,少有针对园地、林地等景观类型的分析。
针对上述问题,本文以雅安市名山区为例,从多个空间粒度出发,选取不同时点的多个景观指数,在景观类型水平层次上探讨茶园景观的粒度效应,对揭示县域茶园景观生态规律和茶园景观格局变化驱动机制具有一定的指导意义。
1 材料和方法
1.1 研究区概况
名山隶属于四川省雅安市,地处四川盆地南西边缘,位于 29°58'~30°16'N,103°02'~103°23'E 之间,东邻成都市蒲江县,南接眉山市丹棱县、洪雅县,西连雅安市雨城区,北壤邛崃市,是“南方丝路”的主要通道和“茶马古道”的起点,处于成渝经济区、攀西经济区、川西北经济区的接合部和川西交通枢纽核心区,是接轨成都的“桥头堡”,也是链接攀西、沟通康藏的“中转站”。辖区面积618.18 km2,辖11个镇和1个街道,192个行政村,总人口28.06万,是一个以茶业作为主导产业的丘陵农业县。
1.2 数据来源及处理
研究所需数据来源于雅安市名山区2002—2018年土地利用现状数据(1∶10 000),原始数据包含AutoCAD的DWG数据、MapGIS的WP数据以及ArcGIS的shp矢量数据,分别采用FME和MapGISK9将DWG数据和WP数据转换为shp矢量数据。利用ArcGIS 10.2提取5期土地利用现状数据中的茶园数据,由矢量数据为栅格数据,以10 m和30 m为间隔设置栅格粒度,将源数据转化为10~150 m以10 m为间隔和150~300 m以30 m为间隔的20个数据,粒度均由初始矢量数据转化。利用Fragstats 4.2软件计算不同粒度下的景观格局指数。
1.3 景观指数分析
综合前人研究结果[7,14,17]和研究区域特点,选取斑块个数(NP)、斑块密度(PD)、景观形状指数(LSI)、最大斑块指数(LPI)、斑块平均面积(AREA-MN)、周长-面积分维数(PAFRAC)、斑块结合度指数(COHESION)和聚集度指数(AI)等8个景观格局指数,从景观斑块的密度特征、聚散性特征、规模特征和形状特征等方面探讨分析不同空间粒度下景观格局指数的差异。借助Fragstats 4.2景观格局分析软件,对不同粒度下的8个景观格局指数进行计算,计算结果使用Excel 2019进行统计分析,借助Origin 2021,选取粒度变化范围(10~300 m)作为 X轴,景观指数计算结果作为Y轴,在Origin中制作坐标图以便后续分析。
1.4 变异系数
利用变异系数(CV)来评价各指标对粒度变化的敏感度,计算公式为[18]:

式中:CV表示不同粒度下景观指数标准差(SD)与平均值(Mean)的比例,为景观指数的尺度测量提供标准度量值。CV值越大代表度量的灵敏度越高。根据前人研究成果[18],可分为5个级别:极敏感(CV>100%)、高敏感(100%>CV>50%)、中敏感(50%>CV>20%)、低敏感(20%>CV>1%)和不敏感(CV<1%)。
1.5 最佳粒度分析法
斑块数量、面积和周长等景观指数是计算大多数其他景观指数的基础,分析其对尺度变化的响应对合理选取研究的最佳粒度具有重要的指导意义[19]。本文选用景观面积损失评价法确定研究区茶园景观的最佳适宜粒度,评价模型为:

式中:E代表面积损失,Ag表示转换后栅格数据的面积,Ab表示基准面积,L为精度损失。
2 结果与分析
2.1 景观指数敏感度分析
由表1可知,不同景观格局指数在不同年份随粒度“粗粒化”呈现出不同变化。其中始终处于高敏感度的指数为斑块平均面积,随粒度增加和时间推移从中敏感度变为高敏感度的指数有斑块指数、斑块密度指数和景观形状指数,这些指数在研究时段内随粒度变化有明显变化;最大斑块指数在研究时段内始终处于中敏感度;始终处于低敏感度的为周长-面积分维数指数,粒度变化对该指数无明显影响;随着时间推移,斑块结合度指数和聚集度指数分别从中、高敏感度变为低敏感度。高敏感指数分别从景观斑块密度、规模和形状的角度反映景观格局,较小斑块信息随粒度增加被较大斑块掩盖,导致这类指数受粒度变化影响较大。
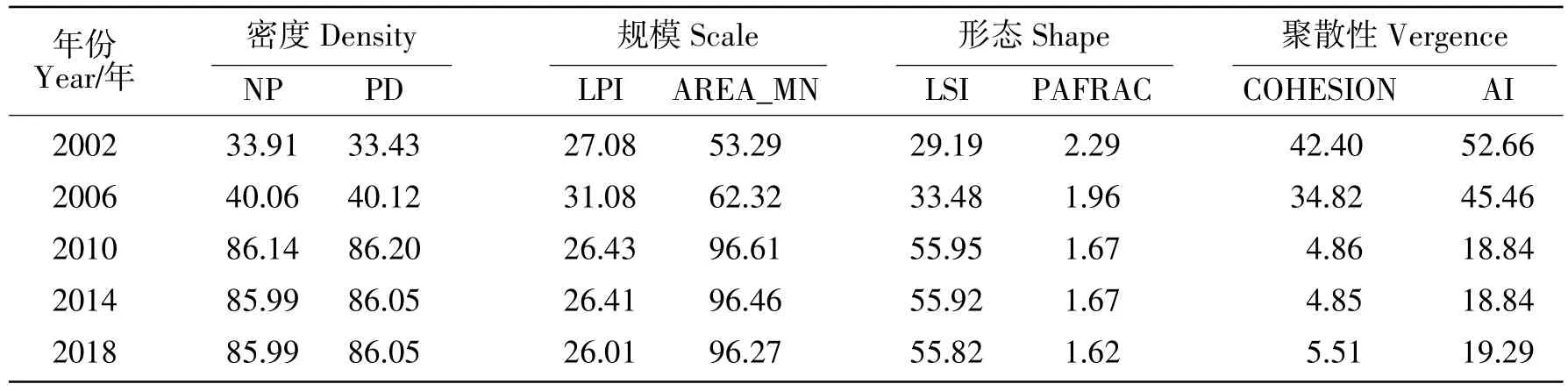
表1 雅安市名山区景观类型水平指数随空间粒度变化变异特征Table 1 Variation characteristics of landscape type level index with spatial granularity change in Mingshan District,Ya'an City
2.2 景观格局指数的粒度效应
2.2.1 斑块类型水平上的粒度效应
2.2.1.1 密度特征变化分析
本文用斑块个数、斑块密度表征茶园景观的密度特征。从图1中可以看出斑块个数和斑块密度变化规律基本一致,两个景观指数的粒度效应曲线呈先线性增加后呈幂函数降低的特征,存在明显拐点20 m和60 m,表明这两个指数具有明显的粒度效应,与敏感度分析结果一致。按密度特征指数数值变化率大小可分为4个阶段,第一阶段为10~20 m线性变化期,景观指数数值随粒度增加而增大。20 m后主要呈降幂变化,景观指数随粒度增加而减小,包括20~60 m快速下降期,60~110 m相对稳定期和110~300 m波动期。
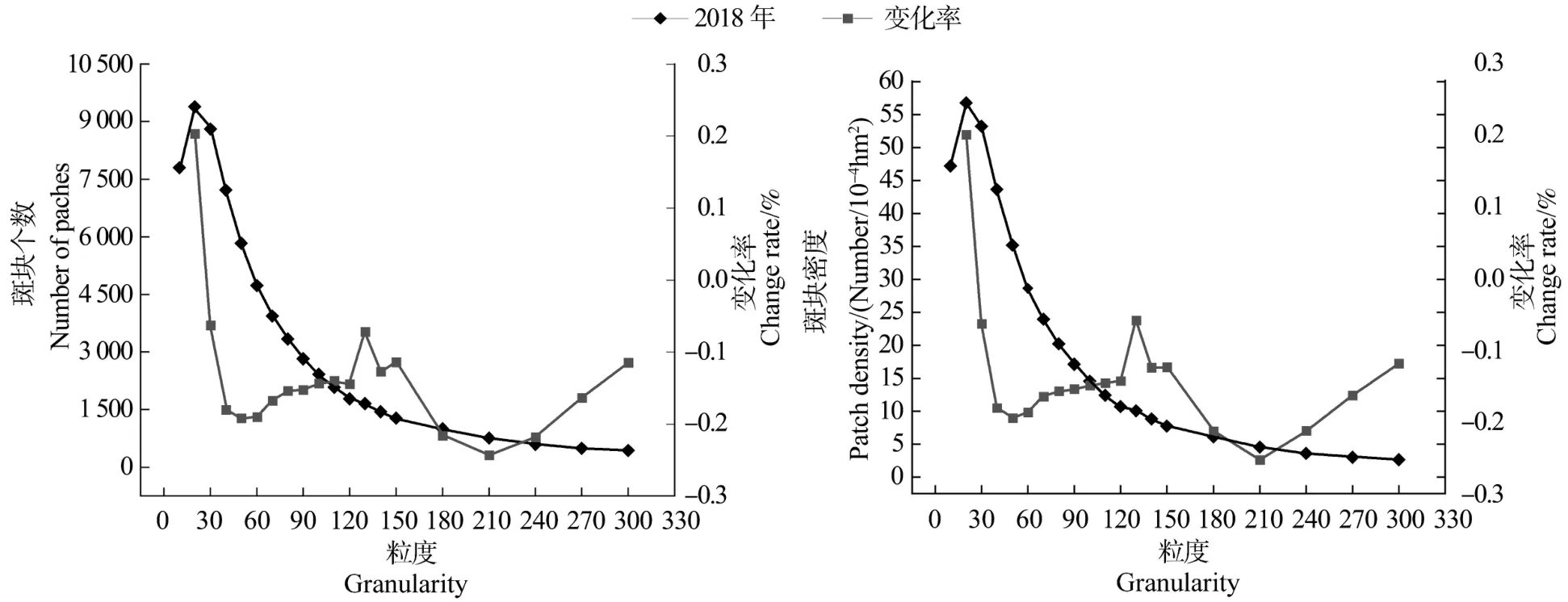
图1 斑块个数和斑块密度的粒度效应Figure 1 Granularity effect of the number of patches and patch density
2.2.1.2 规模特征变化分析
随着粒度增加,最大斑块指数数值呈波动变化趋势(图2),具有多个明显转折点,粒度效应曲线缺乏明显的规律性,在研究粒度范围内主要呈“升-降-升-降”的变化特征,表明茶园斑块优势度无明显的适宜粒度域。
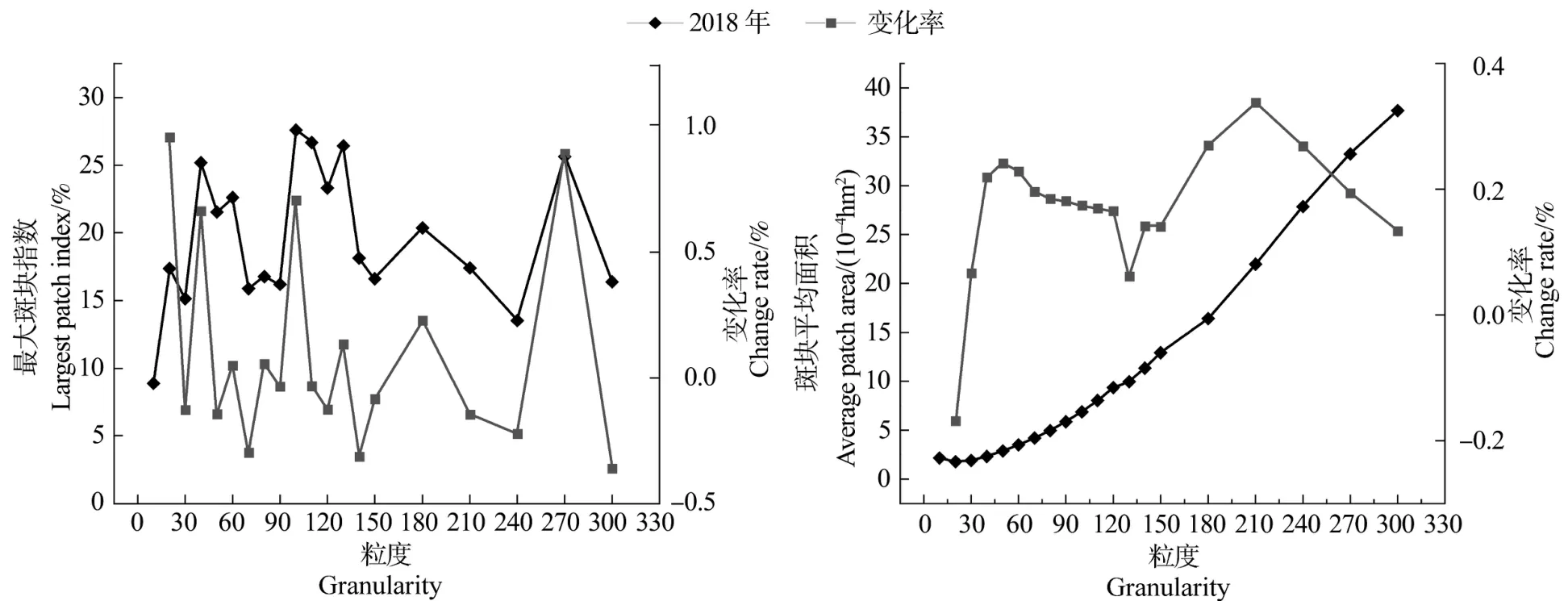
图2 最大斑块指数和斑块平均面积的粒度效应Figure 2 Granularity effect of largest patch index and average patch area
由图2可知,表征斑块破碎度的斑块平均面积指数随粒度增加而增加。根据不同粒度下指数数值变化特征,可以分为4个变化阶段。第一阶段10~60 m和120~210 m为快速上升期,60~110 m为稳定上升期,210~300m为增速降低期。总的来说,随着粒度的粗化,大斑块争夺小斑块导致茶园的平均斑块面积增加,景观的破碎化程度降低。
2.2.1.3 形状特征变化分析
由图3可知,景观形状指数数值随粒度的增加而减少,呈明显的降幂函数关系,60 m为明显拐点。表明随着粒度的增大,斑块形状逐渐变得规则,与粒度增加不断融合周围小斑块导致斑块形状趋于单一有关。根据景观形状指数的变化率可知,景观指数数值在10~60 m和120~300 m范围内变化明显,在60~120 m范围内趋于稳定,变化率在0.02%以内。
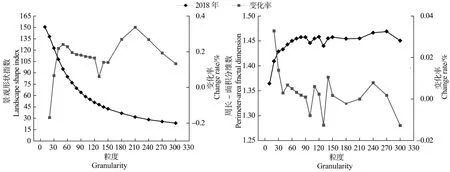
图3 景观形状指数和周长-面积分维数的粒度效应Figure 3 Granularity effect of landscape shape index and perimeter-area fractal dimension
从粒度效应曲线看,周长-面积分维数总体呈先增加后稳定的趋势。表明随粒度增加,斑块的几何形状越趋向简单,受人为干扰的程度越大。数值变化率要呈波动变化,在40~90 m范围内较为稳定。
2.2.1.4 景观空间构型变化分析
由图4可知,斑块结合度指数明显转折点为100 m,指数数值随粒度增加主要呈下降趋势,局部呈上升趋势。斑块结合度指数可衡量某一景观类型的自然连接程度,反映斑块空间连通性[19]。结果表明斑块结合度指数无明显的适宜粒度域,随粒度增加,茶园景观空间连通性较差。
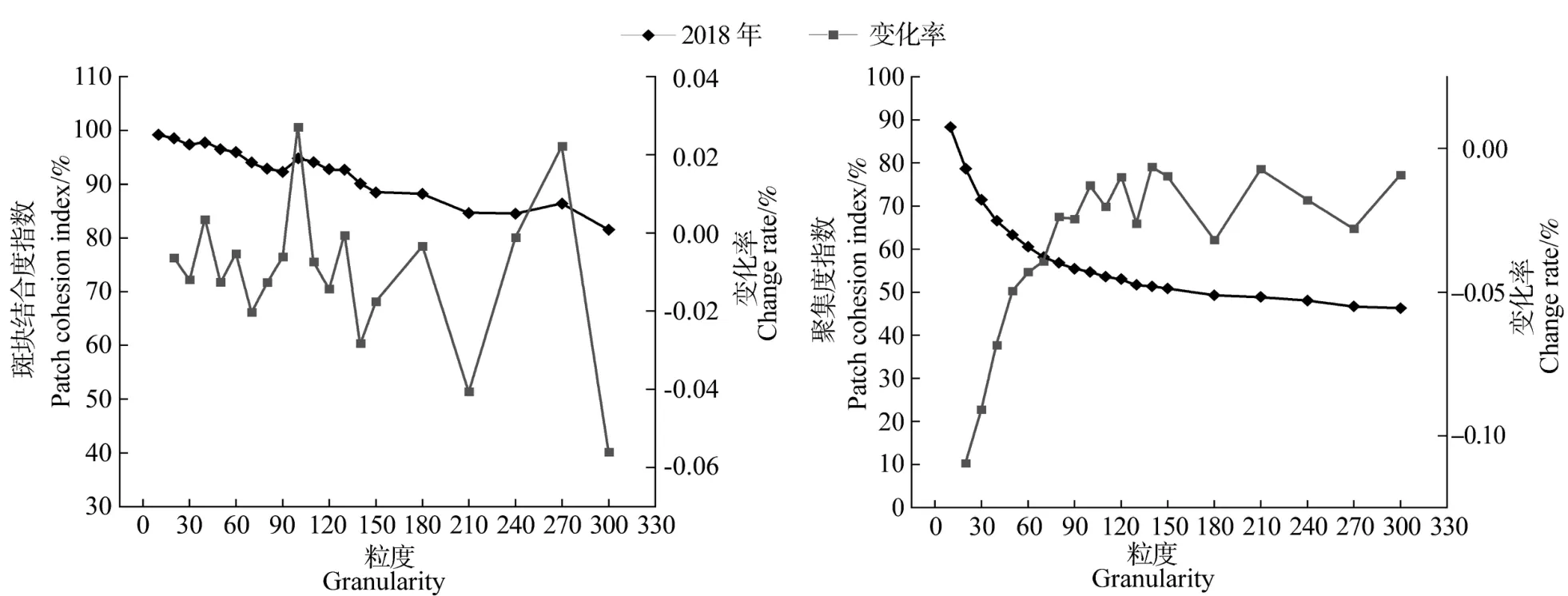
图4 斑块结合度指数和聚集度指数的粒度效应Figure 4 Granularity effect of patch cohesion index and aggregation index
聚集度指数粒度效应曲线平滑(图4),指数数值随粒度增加而下降。聚集度指数可以反映茶园景观斑块的聚散性和空间组合情况,其粒度效应表明茶园斑块空间分布分散。聚集度指数的变化率全部为负值,其中10~70 m为明显下降期;70~300 m为稳定下降期,变化率均小于0.05%。总的来说,名山区茶园景观斑块随粒度增加,空间分布趋于分散化,茶园景观的连通性降低。
2.2.2 景观指数随时间变化的粒度效应
为探寻茶园景观随时间变化的粒度效应,构建以时间为横坐标,不同粒度下茶园景观格局指数数值为纵坐标的曲线图。结合景观类型水平下粒度效应分析结果,选取30 m和60 m两个粒度间隔,发现随着时间的推移,不同粒度下的景观指数呈现相似的粒度效应(图5)。第一类景观指数数值在2010年前呈现出先随时间发展由慢到快地上升,2010年后数值基本不变,包括斑块个数、斑块平均面积指数、景观形状指数、周长-面积分维度指数、斑块结合度指数、聚集度指数(30 m除外)等6个景观指数。其中,斑块个数、景观形状指数是粒度越小变化越明显,其余指数则是斑块越大变化越明显;斑块密度指数数值除30 m粒度外,均在2010年之前先随时间增加而下降,2010年后趋于稳定,表明茶园景观破碎度随着时间发展降低,景观异质性降低;最大斑块指数数值在2002—2006年小幅度下降,2006—2010年快速上升,2010—2018年基本不变,粒度越大变化越明显,表明近年来茶园斑块面积变化不大,茶园景观优势度已基本稳定。
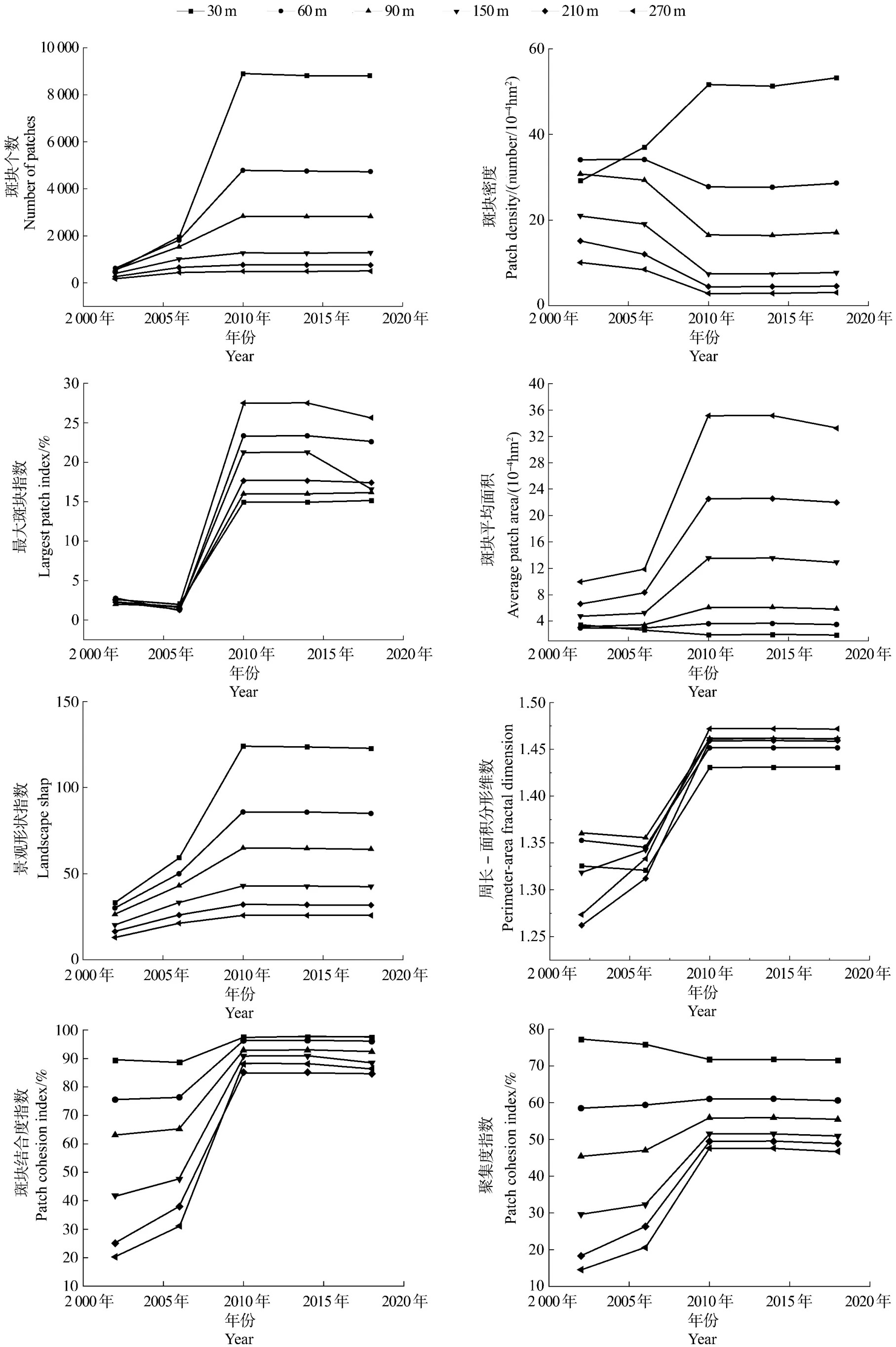
图5 景观指数随时间变化的粒度效应Figure 5 Granularity effect of landscape index over time
综上,针对不同景观指数在时间上的粒度效应主要分为两类:一类是随时间发展指数数值先增加后稳定,且空间粒度越大,景观指数数值变化越明显,包括最大斑块指数、斑块平均面积指数、景观形状指数、周长-面积分维度指数、斑块结合度指数和聚集度指数;另一类是随时间发展指数数值先下降后稳定,空间粒度越小,景观指数变化越明显,包括斑块个数和景观形状指数。这表明,近年来在人为活动影响下,名山区茶园空间分布集聚程度增加,形状趋于规则化,规模化程度有所提升。
2.2.3 适宜粒度范围的确定
不同景观类型的适宜粒度存在差异,空间粒度的选择会使斑块分割影响景观分析结果的科学性和合理性。当景观指数波动较大或出现明显转折时,景观特征会发生较大变化,适宜空间粒度范围内的景观指数变化相对平稳,可以保证空间的边界信息失真度减小,景观格局特征保持相对稳定状态[20]。根据各景观指数的粒度效应曲线变化特征,将大多数景观指数的第1个变化相对稳定的空间粒度范围作为适宜粒度域。综合景观类型指数的CV值与景观指数粒度效应变化规律可知,在分析名山区茶园景观格局时,应采用多数景观指数处于稳定的60~120 m粒度域。
由图6可知,不同时点下景观面积损失度粒度效应不同,总体呈波动变化。其中,2002—2006年间景观面积损失度随粒度增加损失度增大,面积损失度波动明显大于其他年份,其中2002年损失度在270 m处超过7%,2006年在210 m处超过3%。2010—2018年间景观面积损失度变化规律趋同,景观面积损失度随粒度增加先小幅度上升再下降最后趋于稳定。粒度越小面积损失度越大,多个年份面积损失度在110 m处首次超过1%。因此,就信息损失模型而言,最佳分析粒度域为10~110 m,最佳分析粒度为10 m。
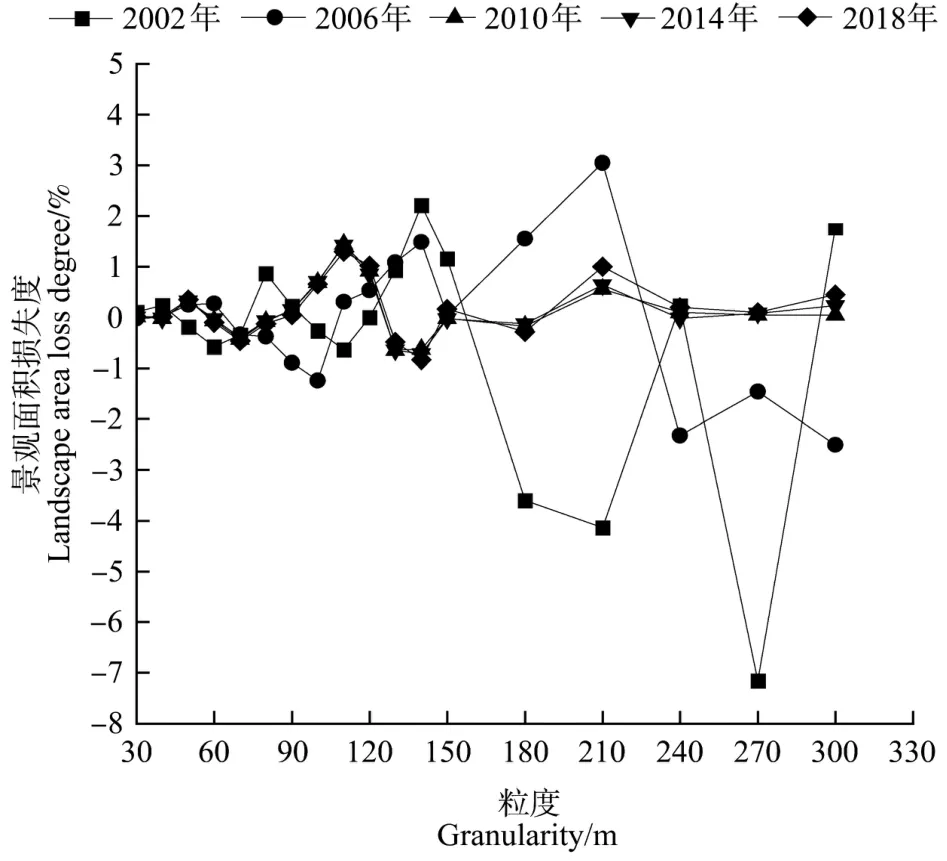
图6 不同时序下景观面积损失度的粒度变化Figure 6 Granularity change of landscape area loss degree under different time series
综合景观指数粒度效应所确定的适宜粒度域分析可知,景观面积损失度在适宜粒度域内景观面积平均损失度呈上升趋势,表明在一定范围内研究粒度越大信息失真度越高,这是由于随着粒度增大容易丢失一些小斑块的空间边界信息造成景观特征发生改变。根据景观面积损失度粒度效应可知,在适宜粒度范围内粒度越小景观面积损失越小。因此,为减少计算量同时保留尽量多的信息,选择60 m作为名山区茶园景观格局分析的最佳粒度。
3 讨论与结论
3.1 讨论
当前,中小尺度区域的尺度效应研究[17,21-22]多采用人工目视解译的遥感数据,存在地类判定不够精确的问题。本文研究对象为茶园,要准确反映该景观类型的粒度效应需要高精度的数据,因此采用名山区不同时点的土地利用现状矢量数据作为数据源,以保证数据的准确性和科学性。同时,不同粒度的栅格数据均由原始数据转换而来,可提高数据计算的可比性。
研究区范围、自然条件以及景观格局的不同,其粒度范围及步长大小选择也不同。在省级尺度上,丁雪姣等[13]结合以25 m为步长在50~350 m对安徽省景观粒度效应进行研究,张妮等[5]以30m为步长并在30~300 m范围内研究扎龙湿地景观力度效应;在市级尺度上,王璐等[23]以30 m为步长在30~300 m范围内研究武汉市景观粒度效应;在县域尺度上,王朋冲等[24]、殷小彤[14]均以30 m为步长在30~300 m范围内进行土地利用景观和居民点景观粒度效应研究。上述研究主要针对研究区景观均采用单一粒度划分。由于大步长会掩盖小步长粒度域的变化规律,小步长会重演大步长粒度域的变化规律[25]。因此,本文进行粒度粗细划分,选择粒度步长为10 m和30 m,不仅能准确分析单一景观类型粒度效应变化还能为研究名山区整体景观格局提供参考。
茶业是雅安市名山区的优势产业,茶园是雅安市名山区的优势地类,因此本文以茶园用地为研究对象进行分析,结果表明雅安市名山区茶园的适宜分析粒度为60~110 m,最佳粒度为60 m。而由于数据限制及区域土地利用差异等情况,现有文献少有针对茶园或园地景观粒度效应的分析,多是根据遥感解译数据,在研究土地利用整体景观时划分了园地这一景观类型,此类研究中各土地利用类型适用粒度域相同。从相关研究来看,李保杰等[26]认为复垦矿区中园地景观指数的适宜粒度域为20~40 m,未提出最佳分析粒度;郭琳等[27]认为巴彦县园地景观指数的适宜粒度域为60~100 m,最佳分析粒度为100 m。综上所述,不同的区域的景观以及不同的景观类型具有不同的景观格局特征,其随空间粒度变化所表现出来的变化规律也不同,景观指数粒度效应存在明显的差异性。
3.2 结论
以雅安市名山区为研究区,利用2002、2006、2010、2014和2018年5期土地利用现状数据,针对茶园景观类型,进行景观指数粒度效应分析,结论如下:
①不同景观指数随粒度变化的响应程度不同,但均表现出一定的尺度依赖性。根据对空间粒度变化的响应度可将景观指数分为高敏感度、中敏感度和低敏感度3类。
②各景观指数随空间粒度的增加主要呈现3种变化趋势:第一类景观指数随着粒度增加而下降,包括斑块个数、斑块密度、景观形状指数、斑块结合度指数和聚集度指数,表明“粗粒化”导致茶园斑块减少,形状趋于规则化,空间聚集度降低且空间分布趋于分散;第二类斑块平均面积指数随粒度增加而增加,景观破碎度降低;第三类景观指数粒度效应无明显规律,包括最大斑块指数和周长面积分维度指数。
③各景观指数在时间上的粒度效应分为两类:一类随时间发展指数数值先增加后稳定,且空间粒度越大,景观指数数值变化越明显,包括最大斑块指数、斑块平均面积指数、景观形状指数、周长-面积分维度指数、斑块结合度指数和聚集度指数;一类随时间发展指数数值先下降后稳定,空间粒度越小,景观指数变化越明显,包括斑块个数和景观形状指数。这表明,近年来,在人为活动影响下,雅安市名山区茶园空间分布集聚程度增加,形状趋于规则化,规模化程度有所提升。
④空间粒度的选择会使斑块分割影响景观分析结果的科学性和合理性,各茶园景观格局指数在60~110 m粒度域内表现稳定,为减少计算量同时保留尽量多的信息确定雅安市名山区茶园景观的最佳分析粒度为60 m。

