基于超声谐波包络Nakagami参数图像的微波消融区域自动分割方法

卓禹心，韩素雅，2*，张榆锋，李支尧，董毅峰

（1.云南省高校高原医学电子信息智能检测处理重点实验室（云南大学），昆明 650091；2.郑州大学信息工程学院，郑州 450001；3.云南省肿瘤医院超声科，昆明 650031）

0 引言

消融是指将加热天线直接插入肿瘤内部并对目标组织加热直到温度达到致死阈值使肿瘤细胞凝固性坏死的治疗方法［1］。为了保证消融手术能够最大范围杀死肿瘤细胞的同时保护健康肝脏组织，在微波消融过程中实时监测消融热损伤区域具有至关重要的作用。最原始的微波消融监测方法是侵入式有损监测，不仅会给患者带来二次伤害增加患者痛苦，且不能有效反映消融过程中温度场的变化趋势［2］，因此微波消融过程中热损伤区域的无创监测方法受到人们的重视。微波消融的无创监测方法主要有核磁共振成像（Magnetic Resonance Imaging，MRI）、超声成像及计算机断层扫描成像（Computed Tomography，CT）。由于超声成像具有无辐射、无损伤且价格低廉等优点，成为对消融过程进行热损伤监测的最常用方法。

为了从超声回波信号中提取更有效的组织消融热损伤区域信息，基于统计模型的参数估计方法成为了诸多学者的研究对象［3］。在微波消融过程中，热效应导致散射体的排列结构发生改变，这些变化会使反向散射信号的分布统计特性发生改变［4］。在与消融监测有关的研究中，已有将Nakagami 概率模型参数化超声回波信号用于评估热损伤的情况［5-8］：Tsui等［5］用Nakagami概率分布模型定量测量超声回波信号的反向散射统计量，发现温度变化与包络信号的Nakagami 参数统计具有相关性；Wang 等［6］对比了消融过程中原始超声回波射频信号的B超图与Nakagami参数图像对于消融热损伤区域的监测效果，实验结果显示Nakagami 参数图像能够更好地显示出消融热损伤程度与区域情况；Rangraz 等［7］利用原超声回波信号估计Nakagami 形状参数和缩放参数来监测高强度聚焦诱导的热损伤区域，发现Nakagami 概率分布的两个参数在消融过程中能够有效监测组织变化情况；Zhou 等［8］对监测消融区域使用超声Nakagami 成像，避免了气泡的干扰，同时提出了复合窗口成像算法，增强了消融区域的可视化。以上方法都是对原始超声回波信号进行Nakagami 参数估计，说明Nakagami 概率分布可以有效地监测消融热损伤。Zhu 等［9］研究表明，在消融后期阶段，生物组织凝固性坏死后，基波对组织温度变化的敏感度降低，使用原始反散射超声包络信号统计微波消融的热损伤情况会产生误差。因此Zhu 等［9］提出了基于超声谐波包络的Nakagami 参数成像方法用于精确估计消融过程中的热损伤区域，证明谐波分量可以更有效地评估微波消融的热损伤。由于Nakagami 参数图像不能精确地估计实际消融区域以及消融边界，所以需要对Nakagami 参数图像进行后处理，Wang 等［10］提出用多项式逼近对消融的Nakagami 参数图像进行后续处理，然而多项式逼近的缺点非常明显：首先，对于不同情况下的消融，多项式逼近的最优阶数是不同的，现在对于多项式逼近的最优阶数并没有定论，Wang 等［10］指出当多项式逼近阶数远远小于像素点时能获得较为准确的逼近效果；另外，多项式逼近过程中的拖尾现象比较严重，会影响监测结果。近期Guan 等［11］研究表明，可以使用高斯逼近代替多项式逼近对消融区域进行监测。高斯逼近处理后的图像接近椭圆形，更符合实际消融情况。相较于多项式逼近，高斯逼近能够提高微波消融监测的有效性以及对消融区域和边界估计的精确性。

针对现有方法无法精确估计消融区域的问题，本文提出了一种基于超声谐波包络Nakagami 参数图像的高斯逼近自适应阈值分割（Gaussian Approximation adaptive Threshold Segmentation，GATS）方法用于监测微波消融过程。首先，对超声谐波包络Nakagami 参数图像进行高斯逼近处理；然后，对高斯逼近获得的图像进行基于P-M（Perona-Malik）、Catte 及中值滤波改进（Median）算法的各向异性扩散平滑的最大类间方差（OTSU）自适应阈值分割［12］估计微波消融热损伤区域；最后，将平滑后图像自适应阈值分割估计的消融区域与实际消融8 min的猪肝消融区域进行相对误差分析，即高斯逼近图像做基于P-M 算法的OTSU 分割能获得最佳的分割结果。与其余监测方法相比，本文监测方法可精确分割出消融区域边界，也能够获得更为精准的消融区域尺寸。

1 本文方法

1.1 Nakagami模型以及参数估计

由于Nakagami 概率参数模型具有良好的拟合性能以及较强的泛化能力，常用于分析超声谐波包络信号［13］。文献［14］中证明了斑点符合Nakagami 分布。Nakagami 概率模型反散射包络的概率密度函数如下：

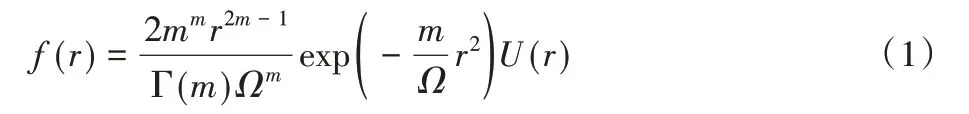
式中：Г（·）是伽马函数；U（x）是阶跃函数。将包络信号的统计方差定义为E（·），则尺度参数Ω和形状参数m可以表示为：

其中：尺度参数Ω与散射能量相关，形状参数m能够反映反向散射包络的概率密度函数形状。

1.2 多项式逼近与高斯逼近

在使用多项式逼近处理Nakagami 参数图像时，首先对轴向方向（沿着超声探头方向）的每一条信号做一维的最小二乘多项式逼近：

接着对横向方向（垂直超声信号的方向）的每一条信号做最小二乘多项式逼近：

其中：fp（V；W）表示多项式处理函数；V表示要多项式逼近处理的矩阵；W=｛i，j｝表示V中需处理向量的行数或者列的列数；Mp表示对Nakagami参数图像做多项式逼近后的图像。

Guan 等［11］提出的高斯逼近处理能够避免多项式逼近的阶数选择及拖尾等问题，处理时与多项式逼近类似，分别在超声探头的轴向和横向做高斯逼近。假设每一个方向的每一条超声信号有n个采样点，可以表示成(xi，yi)(i=1，2，…，n)，令X是均值为λ、方差为σ2的高斯分布，高斯分布的连续概率密度函数［12］为：

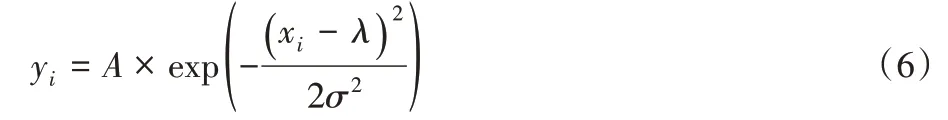
式中A表示高斯函数的幅度，对式（6）两边做对数压缩：

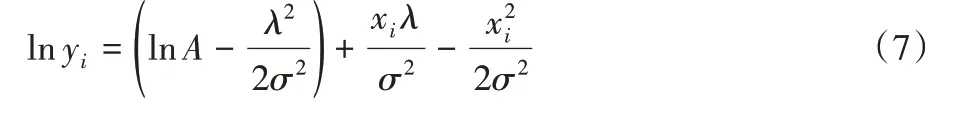
令式（8）表示为矩阵形式，如式（9）：

可进一步简化为：

通过对式（9）解方程得到：

其中：B为式（9）的最小二乘解，通过参数组B可以求得高斯函数的均值λ和方差σ，从而得到对应的高斯函数，并对信号进行高斯逼近处理。

1.3 基于各项性扩散平滑的自适应阈值分割

各向异性平滑常用的算法模型有P-M 算法、Catte 算法及Median 算法。P-M 算法针对各向同性扩散在去噪的同时会模糊图像的边缘，在传统的热扩散基础上，提出了基于非线性偏微分方程的新模型称为各向异性扩散模型，可以表示为：

其中：div 为散度算子，∇为梯度算子，||表示幅度，c(|∇I|)表示扩散系数方程。I0是原始图像，引入时间算子t，证明了降噪的过程与扩散的持续时间相关。图像的边缘一般具有较大的梯度值，所以在图像边缘设置较小的扩散系数实行较弱的平滑，平坦区一般具有较小的梯度值，则在图像平坦处设置较大的扩散系数实行较强的平滑。由于梯度值与扩散系数的关系，提出了两种扩散方程：

式中：k是梯度阈值，在P-M模型中，扩散的程度是由像素点梯度绝对值的大小以及在模型中设定的梯度阈值所决定。Catte模型使用高斯滤波后的平滑梯度代替原始图像的梯度模，可以表示为：

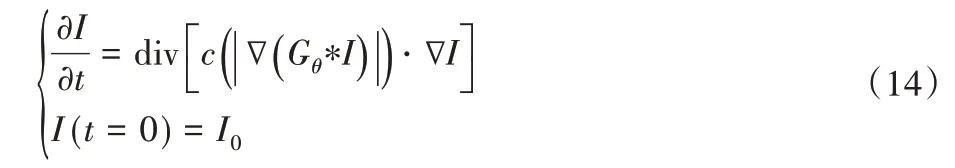
式中：Gθ表示了标准差为θ的高斯函数，“*”代表了卷积过程。Median模型使用自适应中值滤波代替高斯滤波对图像进行处理，然后在扩散系数中加入拉普拉斯算子，可以表示为：

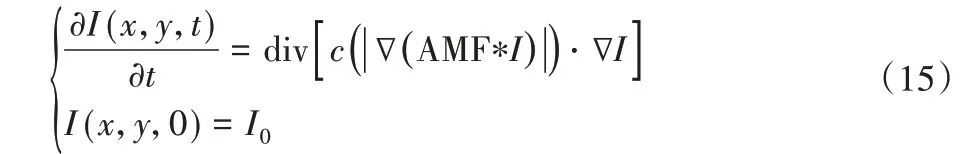
式中：AMF为中值函数。扩散系数如下：

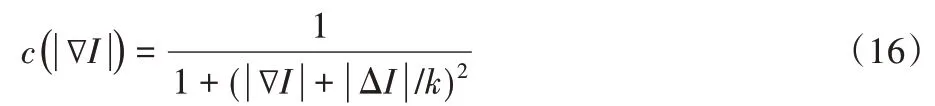
其中Δ 表示拉普拉斯算子。为了能够分割出估计消融区域，本文使用了OTSU 法对平滑图像进行阈值分割处理，是一种自适应的阈值确定方法。它按图像的灰度特性将图像分成背景和目标部分。背景和目标之间的类方差越大，说明构成图像的两部分的差别越大，当部分目标错分为背景部分或者是背景部分错分为目标都会导致两部分差别变小，因此使用类方差最大的分割的错分概率很小。对于图像I(x，y)，用T来表示目标和背景的分割阈值，属于目标部分的像素点数占整幅图像的比例用ρ0来表示，用μ0来表示其平均灰度；用ρ1来表示属于背景像素点占整幅图像的比例，用μ1来表示其平均灰度。图像总的平均灰度被记作μ，用g来表示类间方差。如果图像的背景亮度较低，且图像的大小为M×N，将在图像中的像素灰度值小于阈值T的像素数量写作N0，大于阈值T的像素数量记作N1，推导过程如下所示：

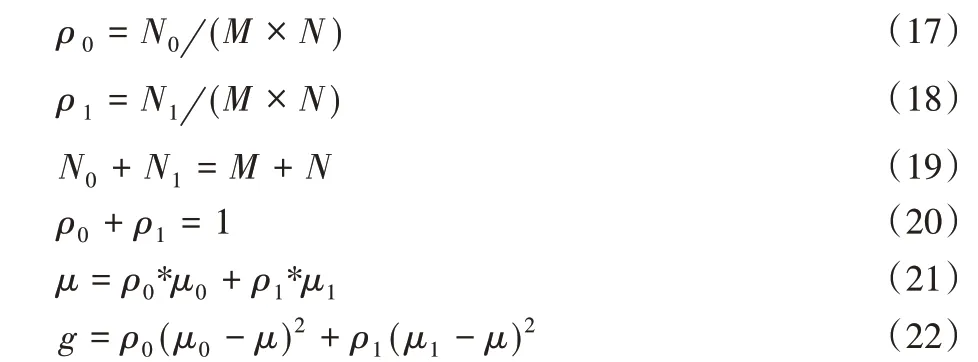
将式（21）代入到式（22）中，得到等价公式如下：

采用遍历的方法得到使类间方差g为最大值的阈值T。

1.4 GATS方法

根据高斯逼近、各向异性平滑以及OTSU 分割提出了GATS 方法用于微波消融的无创、精确监测。GATS 方法首先是对Nakagami 参数进行多项式逼近以及高斯逼近，得到逼近图像；再对逼近图像进行基于各项异性平滑的自适应阈值分割，获得分割后的估计消融区域。对采集到的射频数据进行处理得到Nakagami 参数图像，再对Nakagami 参数图像进行GATS处理的流程如图1所示，GATS流程由虚线框框出。

图1 GATS方法流程Fig.1 Flowchart of GATS approach

2 实验与结果分析

2.1 实验系统搭建

为了验证本文提出的基于超声谐波Nakagami 参数图像的GATS 方法对微波消融组织热损伤情况进行监测的有效性，对10 例离体猪肝组织进行微波消融实验。微波消融实验，选择徐州宝兴医疗设备有限公司生产型号WB-3100 的微波消融仪，并选用型号为Z-8 的治疗热凝器与微波消融仪进行配套使用。再准备一个中国江苏电器电子公司生产型NR-81530 的热电偶温度计用于监测猪肝样本在微波消融实验过程中的温度变化情况。使用Sonix Tough 超声系统实验选择研究模式以及型号为L14-5W/60 的超声探头用于采集离体肝脏消融区域的超声回波射频信号。对回波射频信号进行信号处理继而得到Nakagami 参数图像，再对参数图像进行GATS 处理用的计算机硬件配置为8 块Intel Core i5 的处理器，8 GB DDR3 的内存以及1 TB 的机械硬盘。计算机的操作系统为Windows 10，在对信号以及图像实施处理的过程中，使用版本为2018a的Matlab进行编程。

2.2 实验过程

选择10 例新鲜的离体猪肝，避开猪肝上的主动脉区域，将其分割成大小为10 cm×8 cm×2 cm 的样本块，将样本平行放置于容器中。为了降低容器底部的强回声，在容器的底部铺设一层厚纸板，并将容器水平固定在位移调节平台上，再将微波热凝器的尖端垂直插入组织内部2 cm 的位置并将其固定，然后在超声探头表面均匀地涂一层医用超声耦合剂，将探头与组织表面紧紧贴住，接着用支架将超声探头固定于猪肝样本的正上方，并确保超声探头的方向垂直于微波天线的方向。将Sonix Touch 超声系统连通电源并进行参数配置，主要相关参数如下：中心频率设置为5 MHz，帧速率设置为15 Hz，采样频率设置为40 MHz，低通滤波器的截止频率为30 MHz，扫描深度为5 cm，声速设置为1 540 m/s，发射正弦信号的周期数设置为2。将微波消融仪连通电源开机，选择治疗模式，并设置输出功率为30 W进行实验。

首先，在开始消融前采集未消融猪肝样本的超声射频回波信号，然后利用微波消融仪对猪肝进行消融。将猪肝样本从室温开始加热至消融阈值60℃，分别采集消融2、4、6 及8 min 的超声射频回波信号并保存，用于生成B 超图以及后续实验处理。首先，使用8 阶的截止频率为8.5 MHz 的巴特沃斯高通滤波器分别从消融2、4、6 及8 min 的超声射频回波信号中提取出谐波分量，并通过希尔伯特变换获得谐波信号包络；接着，对谐波包络使用Nakagami 概率模型进行参数化处理，得到Nakagami参数图像；然后，对Nakagami参数图像进行高斯逼近处理，初步估计消融区域并与多项式逼近的结果进行比较；再分别使用P-M、Catte 及Median 算法对高斯及多项式逼近图像进行平滑预处理，再对预处理后的图像进行OTSU自适应阈值分割，估计出较为精确的消融区域。最后，将Nakagami 图像进行GATS 后估计的消融区域与消融8 min 的组织沿超声平面切开后的实际消融区域进行误差对比。

2.3 结果分析

为了验证基于超声回波谐波包络Nakagami 参数图像的GATS方法对微波消融监测的有效性，首先通过搭建的实验系统采集10 例离体猪肝样本组织消融2、4、6 及8 min 的超声回波信号，获得每个时间节点下的谐波B超图像。

图2～3展示了其中两例猪肝样本分别消融2、4、6及8 min的谐波B超图像。

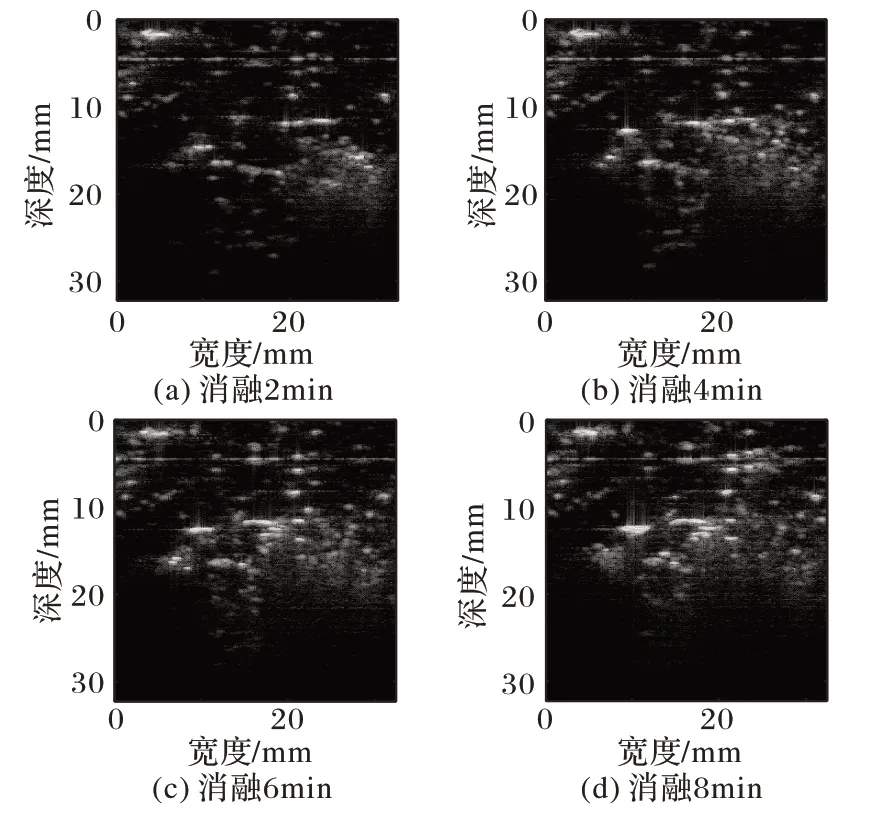
图2 猪肝样本1消融至不同时间的谐波B超图像Fig.2 Harmonic B-ultrasound images of pig liver sample 1 ablating for different time

从图2～3 消融2 min 的谐波B 超图能够看出，在高亮的消融区域周围出现了一些亮斑，并且随着消融时间的增加高亮的消融区域范围会逐渐扩散。但由图2～3（（b）～（d））还可以看出，消融4 min 以后高亮的消融区域边界变得模糊，且在远离探头的方向并未成功呈现消融区域。在消融过程中高亮区域容易被肝脏气泡以及组织凝固性坏死影响产生阴影效应从而影响成像，因此随着消融时间的增加，谐波B超图像难以描述消融区域的变化。

图4～5展示了这两例猪肝样本分别消融2、4、6及8 min的谐波复合Nakagami 形状参数图像，图中颜色由浅变深表示区域温度由低到高。对比图4～5 可以看出，随着消融时间的增长，组织消融区域温度逐渐上升且热损伤区域逐渐扩大。对比猪肝样本1 和样本2 的结果可以看出，图3 中的温度较高的部分范围更大，消融区域及消融边界更明显。对比B 超图像和参数图像可以看出，Nakagami 参数图像能够比B 超图更清晰地呈现出消融的区域，将正常组织和热损伤区域分开。

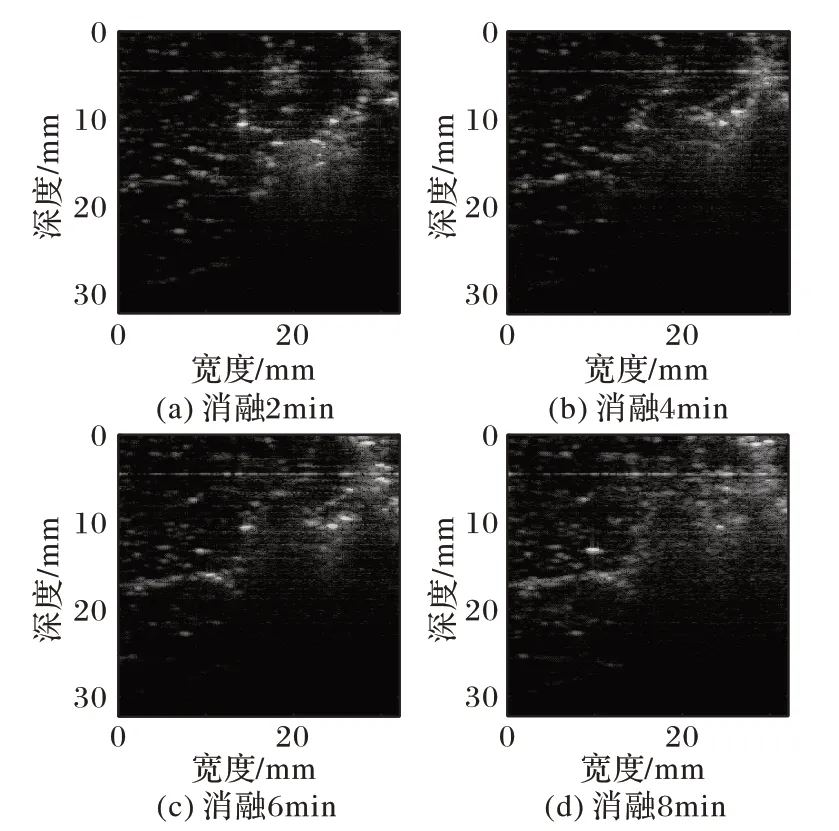
图3 猪肝样本2消融至不同时间的谐波B超图像Fig.3 Harmonic B-ultrasound images of pig liver sample 2 ablating for different time

图4 猪肝样本1消融至不同时间的谐波Nakagami参数图像Fig.4 Harmonic Nakagami parameter images of pig liver sample 1 ablating for different time

由于Nakagami 参数图像不能准确地估计消融范围以及边界，消融区域的可视化程度较低，因此，本文对消融2、4、6、8 min 的Nakagami 图像分别进行了多项式逼近与高斯逼近处理。

图5 猪肝样本2消融至不同时间的谐波Nakagami参数图像Fig.5 Harmonic Nakagami parameter images of pig liver sample 2 ablating for different time

图6～7 展示了猪肝样本1、2 消融不同时间的Nakagami 参数图像进行多项式逼近的结果；图8～9呈现了猪肝样本1、2消融至不同时间的Nakagami 参数图像进行高斯逼近的结果。对比消融2～8 min逼近后的图像都够清晰地看出，消融区域随时间增加明显变大，且颜色较深区域增多消融程度增强，能够有效监测温度场的变化。对比多项式逼近和高斯逼近方法的结果可以看出，多项式逼近的结果拖尾现象严重，且由于噪声的干扰，多项式逼近图像消融区域的形状并不规则；高斯逼近图像避免了以上问题，获得了更有效的消融区域。由于消融区域可以近似为一个圆形区域，高斯逼近后的结果更符合微波消融过程。

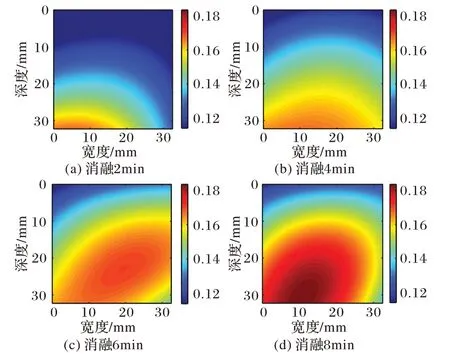
图6 猪肝样本1多项式逼近图像Fig.6 Polynomial approximation images of pig liver sample 1

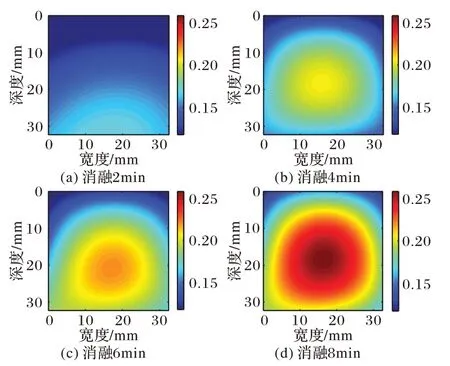
图7 猪肝样本2多项式逼近图像Fig.7 Polynomial approximation images of pig liver sample 2

图8 猪肝样本1高斯逼近图像Fig.8 Gaussian approximation images of pig liver sample 1

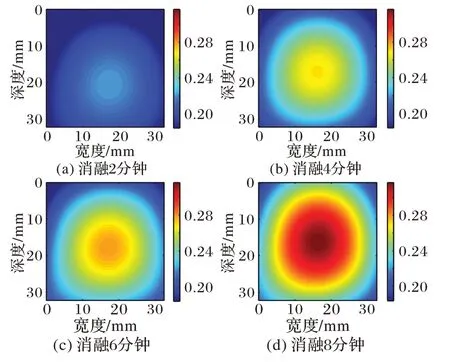
图9 猪肝样本2高斯逼近图像Fig.9 Gaussian approximation images of pig liver sample 2

为了估计消融区域及热损伤程度，首先对消融8 min的多项式逼近图像及高斯逼近图像分别进行基于P-M 算法、Catte算法及Median 算法的各向异性平滑预处理，结果如图10～13所示。

由图10～13 与图6～9（d）对比可知，各向异性平滑能在有效平滑噪声的同时较好地保留边缘信息，分层亦更加明显。由于对图像进行各向异性平滑在对图像进行平滑去除噪声的同时也减少了直方图不连续的现象，从而降低了阈值选择的复杂度，为更精确地分割出估计消融区域做出了铺垫。

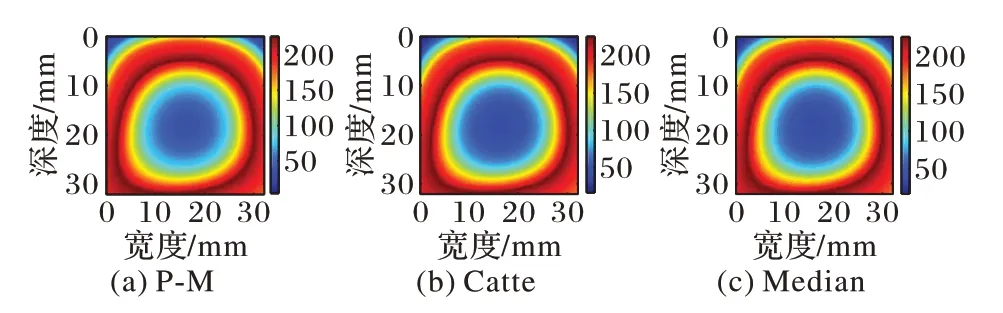
图10 猪肝样本1多项式逼近图像平滑结果Fig.10 Smoothing results of polynomial approximation image of pig liver sample 1

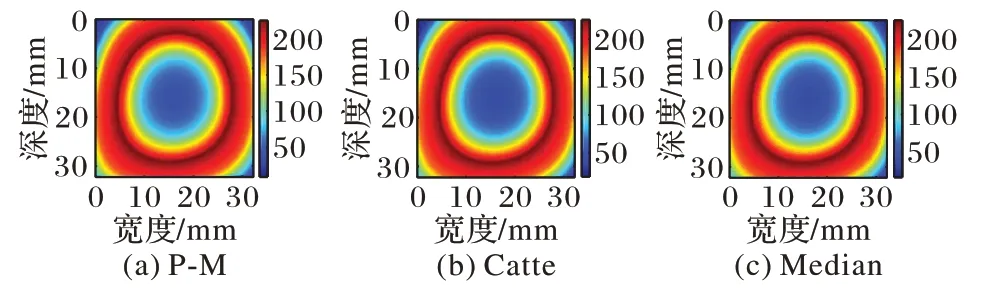
图11 猪肝样本1高斯逼近图像平滑结果Fig.11 Smoothing results of Gaussian approximation image of pig liver sample 1

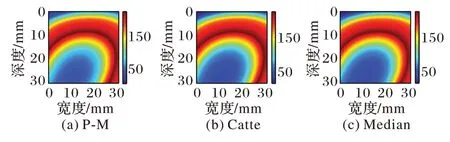
图12 猪肝样本2多项式逼近图像平滑结果Fig.12 Smoothing results of polynomial approximation image of pig liver sample 2 is smoothed

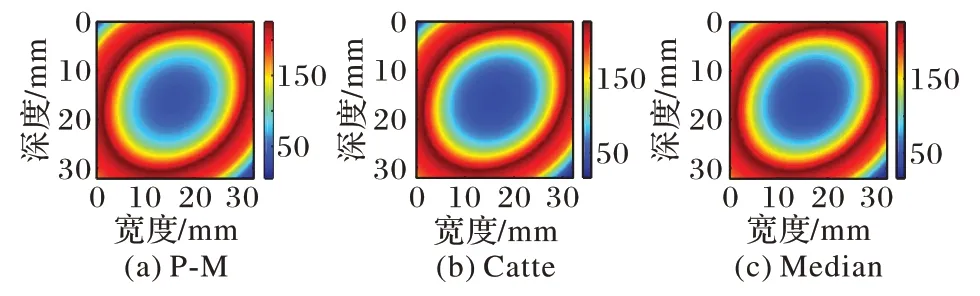
图13 猪肝样本2高斯逼近图像平滑结果Fig.13 Smoothing results of Gaussian approximation image of pig liver sample 2

为了能够精确估计消融区域，并且更好地辨别出不同处理方法下的估计消融区域与实际猪肝消融区域的误差大小，对平滑后的图像进行OTSU自适应阈值分割。

图14 为猪肝样本1、2 消融至8 min 时刻的实际照片，图15～18展示了肝脏样本1、2消融至8 min时刻图像的自适应阈值分割结果。

图14 猪肝样本消融至8 min时的实际照片Fig.14 Actual images of pig liver samples ablating for 8 min

图15 猪肝样本1多项式逼近平滑图像分割结果Fig.15 Segmentation results of smoothed polynomial approximation images of pig liver sample 1

图16 猪肝样本1高斯逼近平滑图像分割结果Fig.16 Segmentation results of smoothed Gaussian approximation images of pig liver sample 1

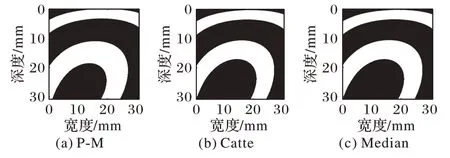
图17 猪肝样本2多项式逼近平滑图像分割结果Fig.17 Segmentation results of smoothed polynomial approximation images of pig liver sample 2

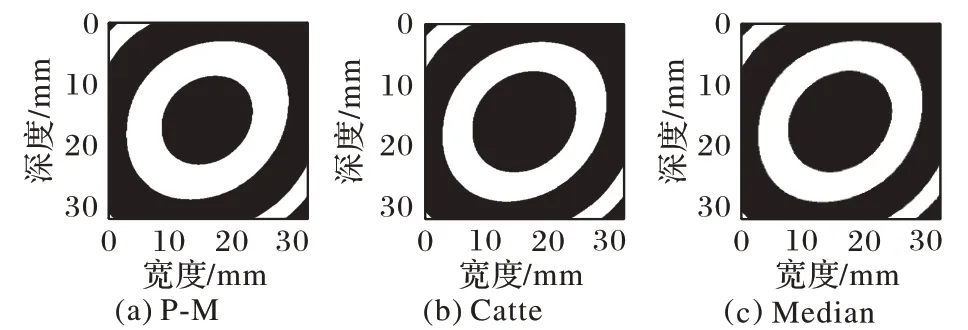
图18 猪肝样本2高斯逼近平滑图像分割结果Fig.18 Segmentation results of smoothed Gaussian approximation images of pig liver sample 2

为了更好地对比估计的消融尺寸与实际消融区域尺寸间的差别，将消融至8 min的肝脏切面实际消融边界对应在自适应阈值分割后图像中圈出，如图15～18 椭圆所示。为了辨别出猪肝样本1、2 消融区域边界，猪肝样本1、2 消融8 min 的实际消融区域边界用椭圆线圈圈出，椭圆线圈以内为实际消融区域。多项式逼近与高斯逼近相比，对高斯逼近图像做基于各向异性扩散的自适应阈值分割后的图像更符合消融过程。

从图15～18 中可以看出，P-M 算法预处理后分割出的估计消融区域最接近实际消融区域，并且，自适应阈值分割后的结果相较于Nakagami 参数图像以及逼近图像干扰显著减少，消融范围以及边界更清晰，监测性能也更好。因此，对超声谐波Nakagami 参数图像进行P-M 算法的GATS 处理后的结果能够精确地估计消融区域以及边界，提高了对消融区域大小以及边界估计的准确性，更具有临床意义。

由图14 实际肝脏切面消融区域对应直尺刻度可知，猪肝样本1、2 消融8 min 实际消融区域的长、短轴分别为21 mm、19.5 mm；23.5 mm、21.5 mm。为了分析不同逼近和预处理方法对阈值分割结果的影响，对猪肝样本1、2 在8 min 的谐波Nakagami参数图像进行多项式、高斯逼近处理，并对逼近图像做基于P-M、Catte、Median算法的各向异性预处理方法的自适应阈值分割，获得的估计消融区域的长、短轴与图14 中猪肝样本1、2消融至8 min实际消融区域的尺寸进行对比分析。

对比表1、2 不同逼近方法的结果，高斯逼近后分割的估计消融区域能获得更好的误差结果，能更精确地分割出消融区域以及边界，更符合实际消融过程。同一逼近方法下，与Catte 算法及Median 算法的各向异性平滑预处理后的分割结果相比，P-M 算法平滑预处理后阈值分割后估计消融区域的形状、大小更接近实际消融区域，与猪肝样本1、2 消融至8 min 实际消融区域长、短轴的误差平均减小了2.95 个百分点、1.15 百分点；6.52 百分点、2.33 百分点。因此，与Catte、Median 平滑算法后的分割结果相比，P-M 算法预处理的GATS方法能够最精确的估计消融区域。

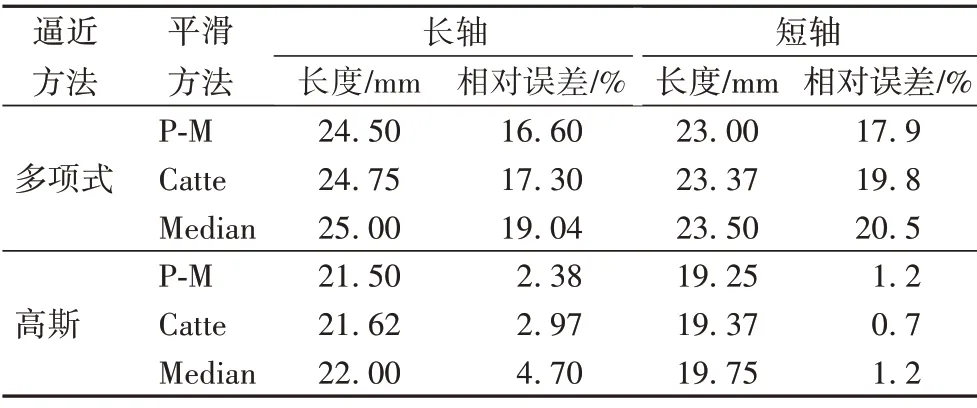
表1 猪肝样本1估计消融区域与实际消融区域的长/短轴相对误差Tab.1 Relative error of long/short axis between estimated ablation area and actual ablation area of pig liver sample 1

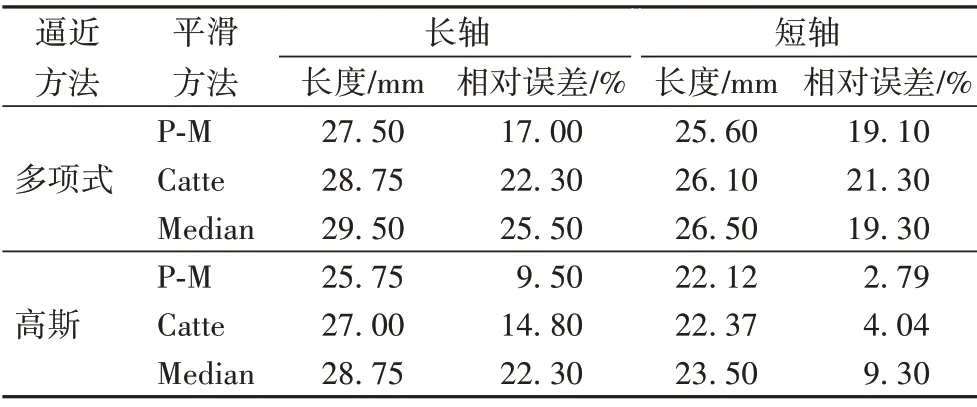
表2 猪肝样本2估计消融区域与实际消融区域的长/短轴相对误差Tab.2 Relative error of long/short axis between estimated ablation area and actual ablation area of pig liver sample 2

为了验证P-M算法的GATS方法的普遍有效性，分析了两种不同逼近方法做了10 组实验后不同算法的各向异性平滑预处理的自适应阈值分割获得的估计消融区域与猪肝样本消融至8 min实际消融区域的误差，如图19所示。

图19 十组猪肝样本消融区域尺寸误差分析Fig.19 Analysis of ablation area size error of 10 groups of pig liver samples

在多项式和高斯逼近的方法下，Catte 算法中采用高斯平滑进行滤波破坏了各向异性扩散的本质，Median 算法中在滤除噪声的同时改变像素点的真实值从而产生误差，因此基于P-M 算法的各向异性平滑预处理后的阈值分割后图像的长、短轴平均相对误差及标准差相对于Catte 算法分别减小了1.92 百分点、1.73 百分点，相对于Median 分别减少了6.24 个百分点、5.67 百分点。综上，P-M 算法的GATS 方法在微波消融过程中的热损伤监测和评估方面呈现出良好的性能，且基于超声谐波包络Nakagami 图像高斯逼近后P-M 算法各向异性平滑的自适应阈值分割方法能够最为精确地对消融区域进行估计。文献［9］方法证明了使用谐波分量估计Nakagami 形状参数，同时生成的Nakagami 参数图像能够较基波更好地对消融区域进行监测，但是谐波的Nakagami 参数图像估计的消融区域非常模糊。目前较为新颖的微波消融监测方法为文献［9］方法、文献［15］方法、文献［16］方法。文献［9］方法以及文献［15］方法是使用Nakagami 分布对消融区域进行估计，文献［16］方法则是利用回波去相关方法对消融过程进行监测。与这些方法相比，本文方法能够分割出清晰、精确的消融区域以及边界，并且背景干扰很少，能够有效提升在实际临床微波消融治疗中对消融区域监测的精度，使手术的成功概率极大提升。P-M 算法的GATS 方法在微波消融过程中的热损伤监测和评估方面呈现出良好的性能，且基于超声谐波包络Nakagami图像高斯逼近后P-M算法各向异性平滑的自适应阈值分割方法能够最为精确地对消融区域进行估计。

3 结语

针对现有方法无法精确有效监测消融过程，本文提出了一种基于超声谐波包络Nakagami 参数图像的高斯逼近自适应阈值分割（GATS）方法。本文研究表明，对超声谐波包络的Nakagami 参数图像使用GATS 方法能够提高对消融过程的监测精度。在最近的研究中，并未提出一个方法能够对谐波的复合Nakagami 形状参数图像进行后续处理并且分割出较为精确的估计消融区域。在本文研究中，对微波消融组织的谐波包络信号的Nakagami 参数图像进行GATS 处理，最后对分割图像与实际猪肝8 min 消融图像进行误差分析，验证了GATS对于微波消融监测的有效性，同时表明了对超声谐波包络的Nakagami 参数图像的高斯逼近图像进行基于P-M 算法的各向异性平滑自适应阈值分割获得的结果能够最为精确估计消融区域以及边界，且没有背景干扰，可以有效地监测和评估消融过程的热损伤情况。由于GATS 方法的精确性、实时性、无创性，其在消融手术中对消融区域的监测精度会极大提高，能应用于临床。由于在本文研究中选择消融区域时避开了猪肝样本的主动脉，并未考虑主动脉对于消融过程的影响，后续工作中将减小超声图像中主动脉产生强回声产生的影响，使GATS更好应用在临床上。