横向整合战略下异质车辆库存路径优化模型
杨华龙,王美玉,辛禹辰
(大连海事大学交通运输工程学院,辽宁大连 116026)
0 引言
在需求不确定的市场环境中,供货商管理库存(Vendor Managed Inventory,VMI)的拉式供应链模式受到了越来越普遍的关注和应用。当区域内多个供货商为各自服务的零售商管理库存时,为了快速响应市场需求,供货商通常会采取横向整合战略,针对库存路径问题(Inventory Routing Problem,IRP)进行协调库存管理与配送优化,确定补货策略和配送策略,以便使物流系统总成本最小化[1]。由于库存与路径存在成本悖反效应[2],加之不同供货商提供的不同品种商品具有需求随机波动[3]、配送软硬时间窗[4-5]和库存服务水平要求[6]存在差异等特点,且第三方物流(The 3rd Party Logistics,3PL)通常拥有多类型车辆资源[7];因此,基于横向整合战略,研究异质车辆IRP随机优化具有重要的现实意义。
目前有关IRP 的研究已有许多成果。Treitl等[8]通过分析配送路径选择以及车辆驾驶速度等对燃油消耗成本的影响,研究了同质车辆配送下的IRP,并提出用综合计算方法来替代只依赖于配送距离计算燃油成本的传统方法。Cheng 等[9]建立了同时考虑环境问题和异质车辆的IRP 模型,在使用综合燃油成本计算方法基础上,对比了同质车辆配送和异质车辆配送产生的成本,实验结果表明使用异质车辆配送可以节约成本。贾涛等[10]基于单一供货商,建立了相同载重量、但贮存温度存在差异的异质车辆配送下的IRP模型。Micheli等[11]则进一步基于碳排放和客户服务水平,研究了一对多模式下异质车辆配送的IRP,并为供应链系统提供最佳解决方案。上述文献都是针对单一供货商的情形,并没有考虑多个供货商联盟的情形。
为了进一步降低供货商的成本,目前供应链中应用比较广泛的两种整合战略是纵向整合和横向整合。其中在VMI模式下的供应链中,由于供货商和零售商分属不同的层级,因此,VMI 优化属于基于纵向整合的供应链战略。El-Wakeel等[12]在考虑零售商库存容量限制建立了多供货商在VMI模式下由同质车辆配送的IRP 模型,Peres 等[13]在此基础上进一步考虑了转运和客户服务水平的因素,建立了多商品的IRP 模型,并为供货商提供库存管理与转运决策。Mirzapour Al-EHashem等[14]研究了VMI模式下异质车辆配送的多对一IRP。
随着政府对碳排放的管控严格化以及追求可持续性发展等新政策的涌现,单独采用纵向整合战略已经无法满足企业管理者的需求[15]。而横向整合战略涉及供应链中同一层级的企业合作[16],具有跨区域性的特点[17],横向整合战略逐渐受到学者和供应链管理者的关注。Juan等[18]将横向整合思想应用到库存路径问题(Vehicle Routing Problem,VRP)领域,建立基于横向整合战略的VRP 模型,采用元启发式算法对比计算了配送车辆的路径成本和排放成本。Vaziri 等[19]考虑了不同商品的特性以及车容的限制,建立了混合整数规划VRP 模型,并使用遗传算法进行求解,得到总利润最大化和运营商之间的利润公平分配的结果。Soysal 等[20]针对由多个供货商和多个零售商组成的物流网络结构,建立了考虑横向整合战略同质车辆配送的易腐品IRP 模型,通过精确求解对比分析了在横向整合与非横向整合战略下供应链系统总成本值。研究表明横向整合战略可以帮助供货商进一步降低成本。但上述文献都假定配送车型单一且未考虑商品配送时间限制。另外,已有研究都假定零售商100%不缺货。然而在横向整合战略下,由于多个供货商配送商品具有多样性的特征,配送车型并非单一,且各类型商品配送时间要求也会存在差异;此外,由于零售商需求具有随机波动的特点,供货商需要为零售商库存设置一定(概率)的服务水平。因此,基于横向整合战略,考虑异质车辆的IRP随机优化研究更贴近于现实要求。
有鉴于此,本文结合VMI 模式下由多个供货商和多个零售商组成的物流配送网络特征,创新性地开展基于横向整合战略的异质车辆IRP随机优化模型研究。
本文的主要创新性研究工作包括:
1)依据公平和有效原则,设计车辆空驶成本由途经的供货商均摊,车辆租用成本、载货行驶成本和超时惩罚成本按各供货商配送货物的比例分摊,各供货商管理的商品库存成本由其自行承担的方法,以利于实现横向整合战略下供货商联盟成员间IRP成本的合理分摊。
2)针对不同类型商品需求随机导致的配送量事先无法确定问题,提出在满足各零售商一定的商品库存服务水平要求下,各供货商应配送到各零售商的商品数量,以利于随机优化模型的鲁棒转化与求解。
3)基于问题及模型的特点,利用需求的累积分布逆函数性质,将IRP 随机优化模型转换为混合整数规划模型,并设计改进的遗传算法进行算例验证分析,以期为供货商联盟下的IRP决策提供有益的参考和实践指导。
1 问题描述
在一个由多个供货商和多个零售商构成的二级供应链系统中,每个供货商配送中心提供的产品不同,即各供货商之间不存在竞争关系。当未实施横向整合战略时,各供货商通过租用3PL 车辆,从各自的配送中心向其零售商提供产品配送服务,每个供货商单独只为自己的客户进行库存路径管理;当实施横向整合战略时,供货商之间组建联盟,供货商联盟共同租用3PL车辆为各个零售商进行商品配送。各零售商商品需求不确定且相互独立,其中各供货商提供不同类型的商品,供货商为零售商提供的商品数量受最大可用库存限制,配送车辆由供货商联盟从3PL统一租用。如,基于横向整合战略,京东的一些供货商签署供货协议组建供货商联盟,为京东线下的各个京东超市提供VMI服务。供货商联盟根据各个京东超市的库存情况,安排租用的3PL车辆,到每个供货商配送中心处装载不同种类商品向京东超市配送。
假设3PL拥有多种类型车辆,不同类型车辆的租车成本、最大载重量、燃油消耗均不同。车辆的起点和终点均位于3PL 所在位置。供货商联盟负责从3PL 租车向零售商配送并承担运费。每种商品产生的库存持有成本由该商品的供货商自行承担。每辆车在每次配送期间最多只能执行一条路线,每个零售商可以有多个车辆为其服务。由此形成的供货商联盟物流网络结构如图1所示。

图1 供货商联盟物流网络结构Fig.1 Logistics network structure of supply alliance
由图1 可见,在横向整合战略下,根据供货商联盟在某一时段结束时刻的供应链系统IRP 方案,车辆1 从3PL 处出发,途径供货商2 和供货商1 集货后,再依次到零售商2、零售商3、零售商4、零售商5和零售商6送货,最后返回3PL处。车辆2 从车场出发,途径供货商M和供货商1 集货后,再依次到零售商N、零售商1、零售商2送货,然后到供货商2取货后,再到零售商4送货,最后返回车场。
由此可见,基于横向整合战略的IRP 随机优化实质便是,供货商联盟在无法预先获得零售商商品需求确定值的情况下,通过设定某一客户服务水平,当商品需求服从正态分布时,为了保证在一定客户服务水平下满足需求,供货商需要确定商品期初库存量的临界值,进而根据该临界值确定商品的配送量,客户服务水平与期初库存量临界值关系如图2所示。
由图2 可见,依据各时段商品需求的均值及其标准差,给定一个客户服务水平,便对应一个期初库存量临界值。由此,以供货商联盟各时段末期望库存成本与车辆配送成本之和最小化为目标,便可以确定各种商品的最优库存和车辆配送计划。
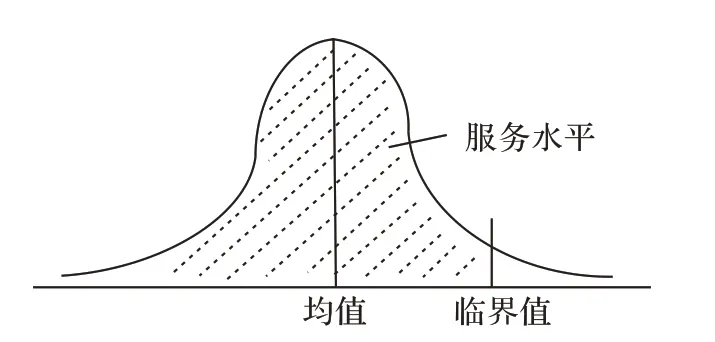
图2 服务水平与期初库存临界值Fig.2 Service level and threshold value of initial inventory
此外,由上述问题描述可知,各供货商管理各自的库存,期望库存成本也由各供货商独自承担;但配送则是由供货商联盟统一租用3PL车辆进行,车辆配送成本、超时惩罚成本需要各供货商分摊。由于3PL 难以准确地评估商品价值,依据公平合理的原则并参考现今收费方式,车辆载货行驶路段产生的配送成本可按各供货商配送商品的重量(或容积)比例进行分摊,车辆空驶路段产生的配送成本由使用该车配送商品的所有供货商平均分摊。
例如,在图1中,车辆1负责供货商1和供货商2的配送任务,车辆1 发生的配送成本分摊如下,在从3PL 处到供货商2、从零售商6返回3PL处两段空驶路径上,车辆1产生的成本由供货商1 和供货商2 平均分摊。从供货商2 装载货物开始,直至到达最后一个送货零售商6,车辆1在上述路径上产生的成本,按照供货商1和供货商2各自配送的商品重量(或容积)比例分摊。车辆2 负责供货商M、供货商1 和供货商2 的配送任务,车辆2发生的配送成本分摊如下,在从3PL处到供货商M、从零售商4返回车场两段空驶路径上,车辆2产生的成本由供货商M、供货商1和供货商2平均分摊。从供货商M装载货物开始,直至到达最后一个零售商4,车辆2 在上述路径上产生的成本,按照供货商M、供货商1 和供货商2 各自配送的商品重量(或容积)比例分摊。
为了便于问题求解,本文结合实际做以下假设:
1)每个时段的零售商需求均服从正态分布;
2)不考虑缺货成本;
3)车辆路线从3PL 开始到结束,每辆车每次最多可以执行一条路线;
4)允许分批交货,每个时段可以有不止一辆车为零售商服务;
5)配送过程中,货物装卸时间相对于运输时间和配送周期足够小,可以忽略不计。
2 模型
2.1 符号及变量
1)集合。
ΔS={1,2,…,i,…,N}:供货商的集合;
ΔC={1,2,…,j,…,M}:零售商的集合;
Δ={0,1,…,i,…,N,N+1,…,j,…,N+M}:配送网络中所有节点集合,0表示3PL;
Ψ={1,2,…,k,…,K}:车型的集合;
Ωk={1,2,…,v,…,Vk}:车型k车辆的集合,k∈Ψ;
Γ={1,2,…,t,…,T}:时段的集合;
Φ={1,2,…,p,…,P}:商品的集合。
2)参数。
E[ ⋅]:期望算子。
Lij:从配送网络节点i到节点j的距离,i,j∈Δ。
Uk:k型车辆的最大载重量,k∈Ψ。
Ijp:零售商j商品p的最大库存容量。
Hjp:零售商j商品p的单位存储成本。
F:每升燃油的价格。
S:车辆行驶速度。
Rk:车型k单位时间的租用成本。
Dijpt:时段t零售商j对供货商i商品p的随机需求量。
Jipt:时段t供货商i可以提供商品p的数量。
α:供货商设定的零售商库存服务水平。
Tjt:时段t车辆从出发至到达节点j的总行驶时间。
Tijt:时段t车辆由节点i直接行驶到节点j的行驶时间。
Wp:配送时间超过软时间窗限制时的单位惩罚成本。
3)决策变量。
xijtvk:在时段t车型k车辆v由节点i直接行驶到节点j,则xijtvk为1;否则为0。
yijptvk:在时段t车型k车辆v由节点i直接行驶到节点j装载商品p的数量。
qijptvk:供货商i在时段t车型k车辆v为零售商j配送商品p的数量。
bijptvk:供货商i在时段t车型k车辆v为零售商j配送商品p,则bijptvk为1;否则为0。
zijpt:表示零售商j处供货商i在前t时段内配送商品p数量与其需求数量之差。
:表示时段t末在零售商j处供货商i商品p的库存数量。
2.2 成本及分摊
1)异质车辆燃油成本。由于异质车辆的车型、载重量以及引擎转速等方面的差异会对燃油消耗产生影响,因此本文引用综合燃油消耗成本函数[12],该函数目前在鲁棒性、可靠性和适用性方面都是最佳的,在时段t车型k车辆v从节点i到节点j路段的综合燃油消耗成本函数Cijtvk为:
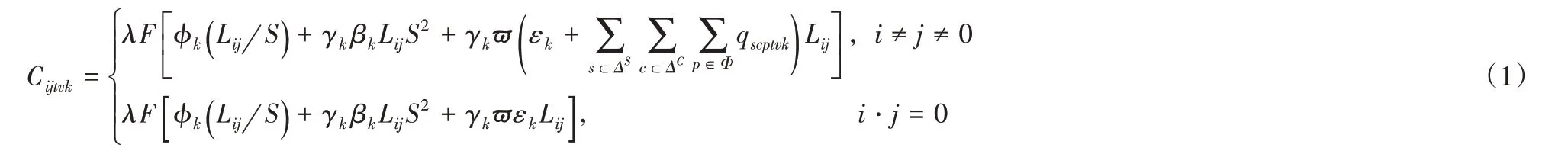
其中:λ为燃油热值系数,ϕk为发动机系数,γk为第k种车型的车辆传动效率系数,βk为第k种车型的空气阻力系数,ϖ为车辆阻力系数,εk为第k种车型的车辆整备质量。
2)配送超时惩罚成本。由于多供货商配送的多种不同类型的商品,某些商品(如生鲜品)会有不同的配送软/硬时间窗限制要求,因此,结合商品特征,可建立在时段t车型k车辆v配送商品p超时的惩罚成本函数Cptvk[20]如下:

3)成本分摊。为了体现供货商之间成本分摊的公平和有效,本文设计分摊原则为,各供货商管理的商品库存成本自行分担,车辆空驶路段成本由供货商平均分摊,车辆载货行驶路段成本、租用成本和商品配送超时惩罚成本按各供货商配送商品的重量(或容积)比例分摊。令:

则在时段t车型k车辆v配送服务的供货商数量为(∀t∈Γ,k∈Ψ,v∈Ωk)。由此,可建立各供货商分担成本函数Ci如下:

2.3 模型构建
根据上述分析,可以建立考虑横向整合下的IRP 随机优化模型[M1]如下:

目标函数式(5)表示使供货商联盟库存路径系统总成本最小化,其中第一部分表示库存持有成本,第二部分表示由燃油消耗成本、超时惩罚成本、租车成本构成的配送成本。约束式(6)表示每个时段末各零售商处供货商在以前时段内配送商品数量与其需求数量之差;约束式(7)表示各时段期末期望库存非负;约束式(8)表示每个时段供货商提供的服务水平限制;约束式(9)表示在每个周期内每个节点处车流量守恒;约束式(10)保证每辆车在每段时间最多执行一条路线;约束式(11)和约束式(12)分别表示车辆不能直接从供货商到3PL 和不能直接从3PL 到零售商;约束式(13)表示车辆从3PL 离开时是空的;约束式(14)表示从供货商处的装载量非负;约束式(15)表示交付给客户的商品数量非负;约束式(16)表示每个时段的装载量都不超过车辆容量限制;约束式(17)表示车辆从供货商处的运货量不得超过其生产量;约束式(18)表示是车辆由节点i直接行驶到节点j的行驶时间;约束式(19)表示车辆由节点i直接行驶到节点j的行驶时间与到达节点所用行驶时间的关系;约束式(20)是配送时间的上限;约束式(21)~(23)表示对决策变量范围的约束。
由于在约束式(6)中含有随机变量Dijpt,而在目标函数式(5)中含有,在约束式(7)中,确定,为此,对式(6)两端取期望值,可得:

此外,由于式(8)属于随机概率约束,表示在每个时段末零售商库存水平非负的概率不小于供货商提供的服务水平,这也意味着在每个时段初零售商库存水平高于该时段需求的概率不小于供货商提供的服务水平。因此,约束式(8)可改写成[20]:

由式(7)和式(25)得:
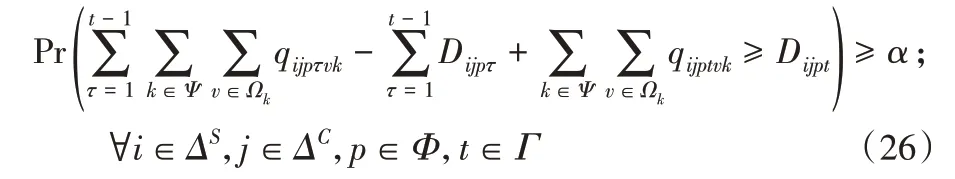
令Dijp(t)=Dijp1+Dijp2+…+Dijpt,Dijp(t)的累积 分布函数记为。于是由式(26)可得:

如果Dijpτ,τ∈{1,2,…,t}相互独立且服从均值为μijpτ,标准差为σijpτ的正态分布,则有

则由式(27)可得:
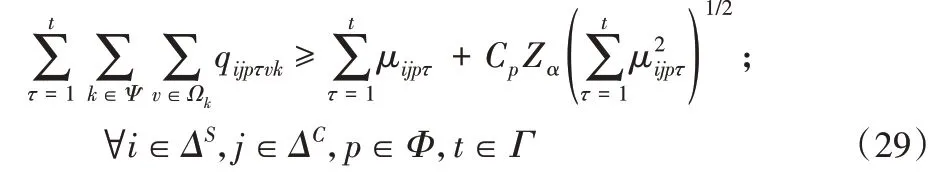
其中:Cp为变异系数,对于每种商品p∈P而言,Cp是常数;Zα是标准正态分布在置信水平为α的系数。
用约束式(24)代替约束式(6),用约束式(29)代替约束式(8),则随机模型[M1]可转化为如下确定型模型[M2]:
目标函数式(5)
约束式(7)、(9)~(24)、(29)。
3 异质车辆IRP模型算法设计
由于IRP 是强NP-难问题,求解方法大多采用启发式算法。遗传算法采用“优胜劣汰,适者生存”的遗传机制具有内在的隐并行性和更好的全局搜索能力;因此,结合模型[M2]的特征,本文设计了改进的遗传算法对其进行求解。
原始的遗传算法交叉率和变异率都设定为一个固定值,在遗传进化中不能进行动态变化,从生物进化的角度上看,虽然原始的遗传算法对种群的环境适应能力进行了模拟,但是不能客观反映种群跟随环境进化时不同时段的要求,忽视了个体发育与遗传行为随环境变化的自适应特性,这会严重影响遗传算法的收敛性能和优化效率。因此,本文根据sigmoid函数求解最小优化问题设计一种自适应启发因子,具体如下:

因此,改进的遗传算法步骤如下:
步骤1 初始化种群。由于求解的关键在于0-1 变量bijptvk,根据供应商是否配送计算出配送矩阵后,可以根据配送量输出相应的配送方案。因此首先定义一个可以代表本文中异质车辆配送问题的染色体序列,在此基础上,进行供货商选择及车辆分配,形成初始配送方案。
步骤2 对每个个体的适应度值进行计算并排序。遗传算法的适应度是用来衡量个体在优化过程中优劣程度,本文为最小化优化问题,根据约束条件使用目标函数倒数的表述方法设置适应度函数,适应度值越高,表明得到的解越好。
步骤3 选择算子。本文使用轮盘赌注选择法,种群中每个个体被选中的可能性与其适应度值成正比。每个个体的适应度值与整个种群适应度值和之比就是个体进入下一代的概率,个体的适应度值越高,轮盘中扇形面积越大,被选中概率就越大。若某个个体为i,其适度为fi,种群的大小为M,则其被选中进入下一代的概率为:

步骤4 交叉算子。采用部分匹配交叉的方法,首先随机选择两个交叉点r1=2和r2=5确定交叉区域,由于交叉后会部分基因会出现重复的情况,因此通过在交叉域外建立匹配关系消除冲突,具体交叉操作过程如图3所示。
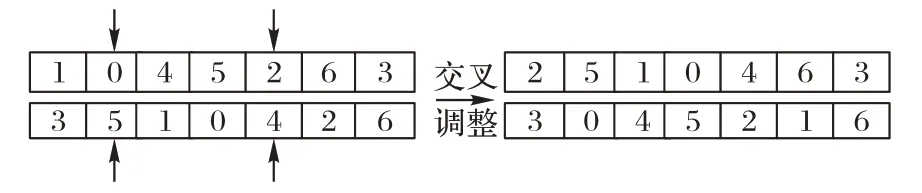
图3 交叉操作Fig.3 Cross operation
步骤5 变异算子。采用个体内部两位互换法,执行变异操作。首先随机选择两个点位r1=2 和r2=5。将其位置对换,这种变异方法能够在较短的进化代数中找到优良基因,具体交叉操作过程如图4所示。

图4 变异操作Fig.4 Mutation operation
步骤6 下一代个体的生成。将父代和遗传进化得到的子代结合,从中选取最优的部分个体作为下次迭代的父代个体。
步骤7 生成最优解。循环步骤2~6,直到达到最大迭代次数,输出最优解。
4 算例分析
4.1 数据选取及计算
假设有两家供货商基于横向整合战略组建供货商联盟,在某区域内为11 家零售商提供VMI 服务,供货商1 提供商品1,供货商2提供商品2。每周为一个决策期(每天为一个时段),联盟租用3PL载重量分别为12 500 kg的重型配送车辆(Heavyduty Vehicle,HDV)和4 000 kg 的轻型配送车辆(Light-duty Vehicle,LDV)为零售商进行共同配送,车辆的行驶速度均为80 km/h,租车成本分别为220 元/h 和100 元/h。燃油价格为5.84元/升,车辆燃油消耗相关参数数据取自文献[12]。对于商品1,配送软时间窗限制为2 h,配送硬时间窗限制为4 h,商品超时惩罚成本为0.07元/(kg·h)。对于商品2,配送软时间窗限制为3 h,配送硬时间窗限制为6 h,商品超时惩罚成本为0.05 元/(kg·h)。所有供货商、零售商和3PL 车场的位置数据均取自文献[21]。每种商品每天的需求服从正态分布,正态分布均值如表1所示。

表1 零售商每种商品每天的需求均值 单位:kgTab.1 Average expected demand for each retailor of each product at each day unit:kg
假设零售商对两种商品的最大库存容量均为10 000 kg,两种商品的库存服务水平为95%。商品1 和商品2 每天的单位库存费分别为0.08 元/d 和0.1 元/d。改进的遗传算法的主要参数设置如下:种群数量为100;最大迭代代数为100;交叉概率为0.9;变异概率为0.1。本文在Pentium i5 1.80 GHz 内存为4 GB 的电脑上,利用Matlab2014a 软件进行数值算例分析,现将本文改进后的遗传算法(算法1)与未改进的遗传算法(算法2)、粒子群算法(算法3)、与算法1 运行时间相同的Cplex 近似解(算法4)和Cplex 精确解(算法5),分别在零售商数量为5 家(零售商1~5),8 家(零售商1~8)和11 家(零售商 1~11)算例规模下进行运算对比,结果如表2所示。

表2 不同算法计算结果Tab.2 Computing results of different algorithms
由表2可见,在不同零售商规模的情况下,算法1在运行时间和解的质量方面均优于算法2和算法3;在相同运行时间下,算法1解的质量也明显优于算法4;当零售商数量为5和8时,算法1 解的质量与算法5 相比,分别相差0.85%和0.76%,当零售商数量为11时,与算法5在最长有效运行时间(21 600 s)下解的质量相差0.59%。上述实验结果表明,本文算法在运行时间和解的质量方面,均优于未改进的遗传算法和粒子群算法;在解的质量方面也明显优于相同运行时间的Cplex近似解算法;与Cplex 精确解算法相比,在运行时间方面具有明显的优势,在解的质量方面相差非常小。因此,本文设计的改进遗传算法求解模型适用且有效。
为验证本文改进的遗传算法可以跳出传统遗传算法容易陷入局部最优和收敛速度慢的缺陷,将改进的遗传算法和改进前的遗传算法迭代收敛效果进行对比,如图5所示。
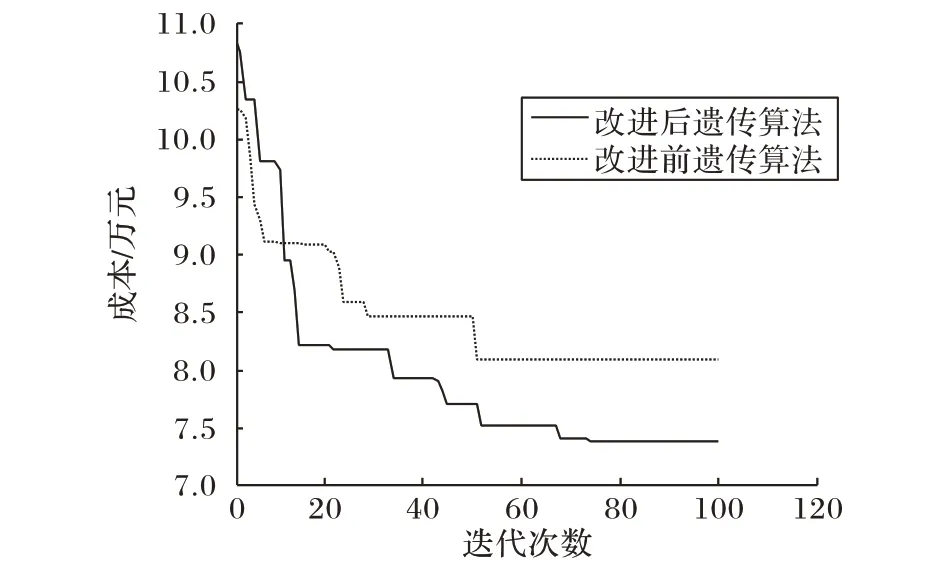
图5 遗传算法改进前后迭代收敛效果及解的质量Fig.5 Iterative convergence effect and solution quality before and after genetic algorithm improvement
从图5 两种算法迭代收敛效果比较来看:改进前的遗传算法收敛速度慢,容易陷入局部最优,且求解质量较差;而改进后的遗传算法能有效地引导算法跳出局部最优,且收敛速度更快,能够快速找到质量更高的解。
为了凸显异质车辆在横向整合战略下对供应链系统各项成本带来的影响,本文将横向整合战略下异质车辆配送与同质车辆配送时的计算结果进行对比,得到供货商联盟的库存持有成本、燃油成本、超时成本以及车辆租用成本等结果如表3所示。

表3 异质与同质车辆配送成本 单位:元Tab.3 Distribution costs of heterogeneous and homogeneous vehicles unit:yuan
从表3 中显示的各项绩效指标数据可以看出,在横向整合战略下,采用异质车辆配送的供货商联盟的总成本明显低于采用同质车辆配送的供货商联盟的总成本。其中,采用同质车辆HDV 配送时供货商的各项成本均高于异质车辆配送的情况。究其原因,是因为异质车辆配送可以根据需求的变化选择不同车型进行配送,减少了货物的积压和车容的浪费,降低了库存持有成本及车辆租用成本,从而降低了供货商总成本。采用同质车辆LDV 配送时除库存持有成本低于异质车辆配送时的对应成本,总成本仍高于异质车辆配送时的成本。究其原因是同质车辆LDV 车容较小且单位租车成本较低,虽然可以避免货物过度积压,但为了满足零售商需求需要租用更多的车辆进行配送,因而造成了燃油成本以及租车成本的大幅度增加,导致供货商联盟的总成本高于异质车辆配送时的供货商联盟的总成本。
在横向整合战略下,异质与同质车辆配送的行驶路径如表4 所示,租用车辆总数、装载率和总燃油消耗量如表5 所示。
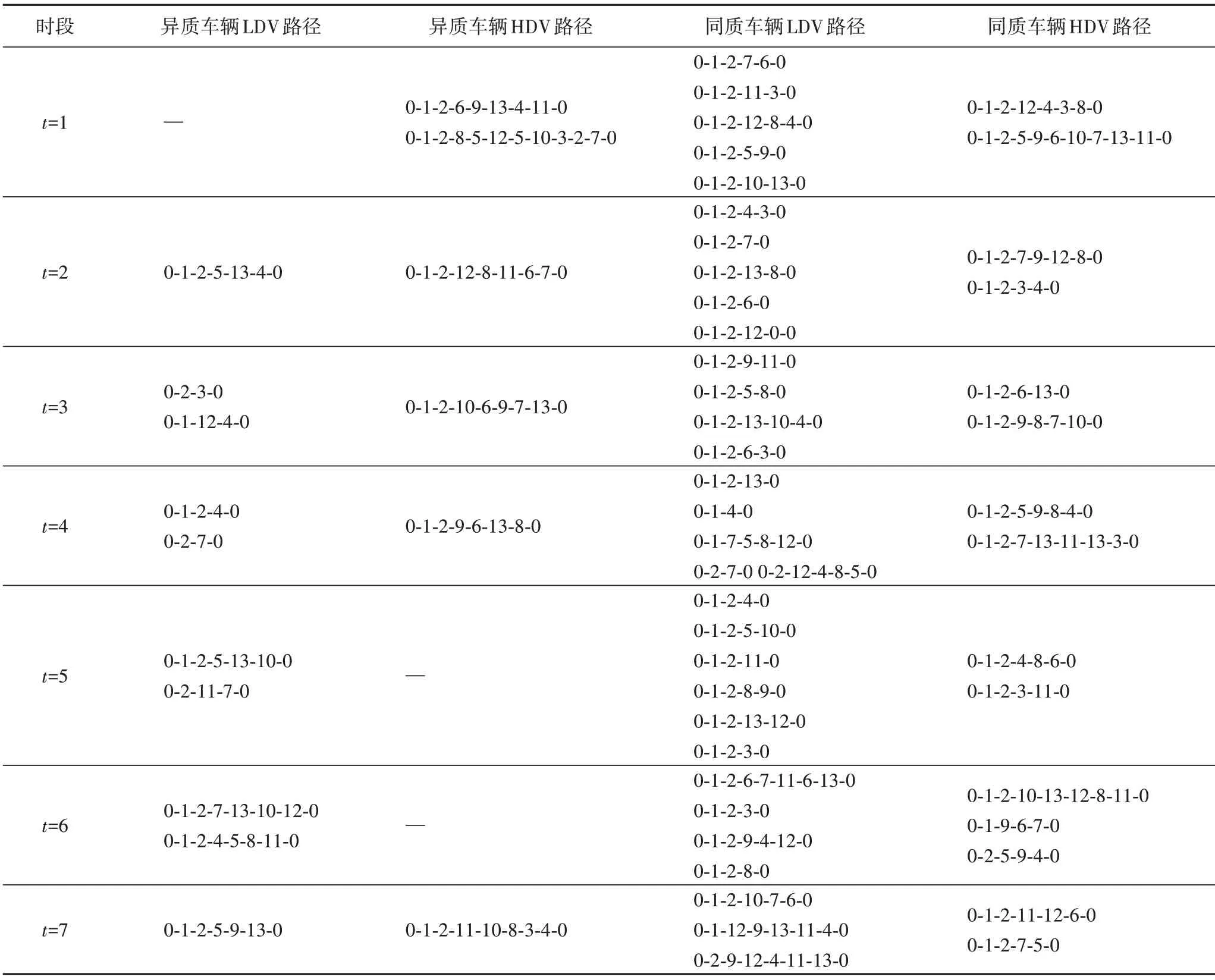
表4 横向整合下异质与同质车辆配送方案Tab.4 Distribution schemes of heterogeneous and homogeneous vehicles under horizontal collaboration
由表4 可见,采用异质车辆配送时,供货商联盟在各时段会根据零售商需求情况租用不同的车辆完成配送,租用车辆总数明显少于采用异质车辆配送时租用LDV 的总数;会略多于租用HDV的总数。
由表5 可见,采用异质车辆配送时,车辆装载率明显高于单独采用同质车辆配送时的装载率;燃油消耗量明显低于采用同质车辆HDV和LDV时的消耗量。究其原因,是由于在异租用质车辆配送方案下,供货商可根据零售商需求租用不同类型车辆进行配送,使车容得以合理利用,更好地平衡库存持有成本和配送成本之间关系,使得配送车辆的燃油消耗得以降低,有利于节能减排。

表5 横向整合下租车方案对比Tab.5 Comparison of vehicle rental schemes under horizontal collaboration
4.2 敏感性分析
在横向整合战略下,各供货商配送商品的数量比例是影响其配送成本的主要因素。为了分析各供货商配送商品数量发生变化时对其所分摊的成本影响,本文在保持两家供货商总商品配送数量不变的情况下,令供货商1配送商品数量占总配送商品数量的比例分别为10%、20%、30%、40%、50%、60%、70%、80%和90%,共计9种情形,对算例进行敏感性分析,得到在横向整合战略下本文成本分摊法、平均分摊法以及非横向整合战略下供货商1和供货商2的总成本结果,如图6所示。
由图6(a)和图6(b)可以看出,无论各供货商配送商品的比例怎样变化,在横向整合战略下,采用本文提出的成本分摊方法,两个供货商的总成本都要低于非横向整合战略下的总成本;但若采用平均成本分摊法,在供货商1(或2)配送商品比例较小时,横向整合的总成本高于非横向整合下的总成本,因而造成横向整合战略不可行。这表明本文提出的成本分摊方法可行且有效。
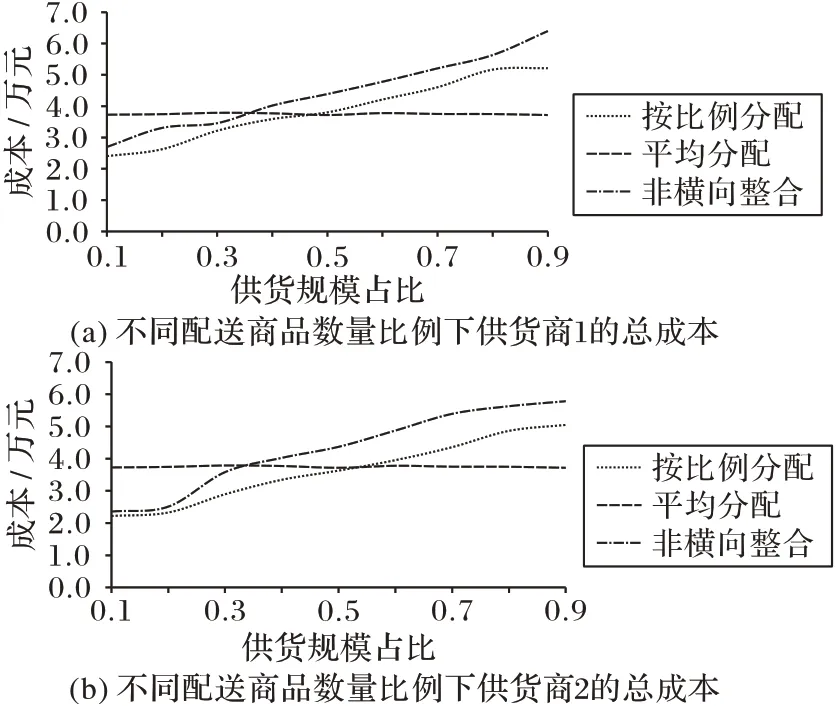
图6 供货商的总成本Fig.6 Total cost of suppliers
为了分析零售商需求波动对供货商联盟总成本的影响,令零售商需求期望值不变,需求变异系数分别取值为0.025、0.05、0.1、0.2、0.3、0.4、0.5,对算例进行敏感性分析,得到异质车辆与同质车辆配送供货商联盟总成本的变化情况如图7所示。
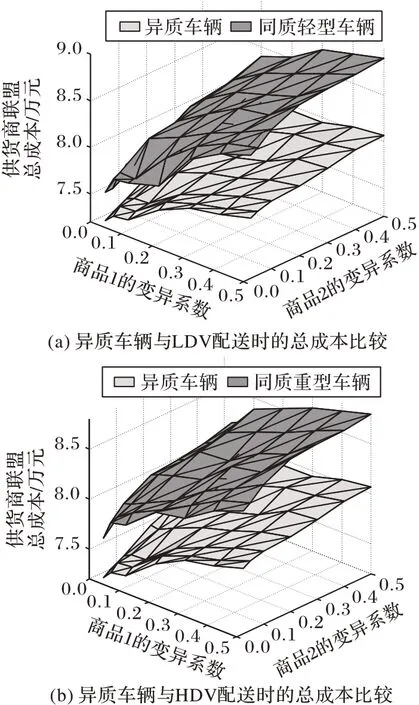
图7 供货商联盟总成本Fig.7 Total cost of supplier alliance
由图7(a)可以看出,无论两种商品需求变异系数如何变化,使用异质车辆配送时供货商联盟的总成本都要低于使用同质LDV配送时的总成本。同样地,由图7(b)可以看出,无论两种商品需求变异系数如何变化,使用异质车辆配送时供货商联盟的总成本都要低于使用同质HDV 配送时的总成本。此外,由图7还可以看出,随着两种商品需求变异系数的单独或同时变大,供货商联盟总成本都会随之增大,且使用异质车辆配送的优势也愈加明显。这是因为一方面,当商品需求期望值不变时,需求波动程度越大,则为了满足一定的库存服务水平要求,零售商各时段末持有的安全库存以及期望库存也越高,因而会导致供货商库存成本升高。此外,需求波动程度越大,供货商则需要配送更多数量的商品,因此供货商配送成本也会升高;另一方面,由于相较于采用同质车辆配送,采用异质车辆配送可使车容得以合理利用,降低配送车辆的燃油消耗和供货商联盟的车辆配送成本,从而降低供货商联盟的总成本。
5 结语
在VMI 模式的供应链中,基于横向整合战略的供货商联盟是一种潜力巨大的合作模式。本文的主要工作就在于设计了供货商车辆配送成本的合理分摊原则,通过考虑零售商商品需求随机波动和库存服务水平要求等因素,建立了多供货商多商品异质车辆IRP 随机优化模型,并在模型确定型转化的基础上,设计了改进的遗传算法,从而有效地实现了供货商联盟下的IRP随机优化。
本研究得到的主要结论包括:1)根据需求变化而选择不同车型进行异质车辆配送,虽然相较于全部选用小型车辆配送可能会增加库存成本,但却能够减少货物积压和车容浪费,可以降低车辆燃油成本、配送超时成本和车辆租用成本,并最终降低了供货商的总成本。因此,需求随机波动下的异质车辆配送更为有效;2)在供货商间商品配送数量比例差异较大时,采用平均成本分摊方法不利于横向整合战略的实施。而采用本文提出的成本分摊方法,无论供货商间商品配送比例差异怎样变化,都可使各供货商总成本得到降低,从而有助于供货商联盟的稳定,实现合作共赢;3)无论零售商商品需求变异系数如何变化,使用异质车辆配送时供货商联盟的总成本都要低于使用同质车辆配送时的总成本。且零售商商品需求变异系数越大,供货商联盟总成本越高,使用异质车辆配送的优势越明显。
依托本文可进一步从多个方面进行拓展研究。库存服务水平与物流系统总成本具有效益背反关系,本文是在库存服务水平给定情形下建立了IRP 随机优化模型,未来可将供货商随机IRP 与库存服务水平进行联合优化研究;另外,由于在许多面向库存(非面向订单)生产的VMI 模式供应链中,需要进行供货商配送中心库存优化。因此,未来可以进一步开展二级IRP随机优化研究,以降低供货商物流系统的总成本。

