基于变分自编码器的异常颈动脉早期识别和预测

黄晓祥，胡咏梅，吴 丹，任力杰

（1.山东大学控制科学与工程学院，济南 250061；2.中国科学院深圳先进技术研究院，广东深圳 518055；3.深圳市第二人民医院神经内科，广东深圳 518028）

0 引言

脑卒中是一种急性脑血管疾病，也是全球第二大致死和第一大致残疾病，它是由脑部血管突然破裂或因血管阻塞导致血液不能流入大脑而引起脑组织损伤的一组疾病，它的发病率在发展中国家仍不断上升［1］。由于它更多的是造成残疾，因此病人需要更长的住院时间和更多的照顾，这对个人和家庭也是一种沉重的负担［2］。据世界卫生组织统计，全球每年约有1 500 万人患脑卒中，预计到2030 年，这一数字还将增加340 万［3］。大量研究表明，颈动脉病变，如颈动脉内中膜厚度增加（Carotid Intima Media Thickness，CIMT）或颈动脉斑块等是动脉粥样硬化性心血管疾病（AtheroSclerotic CardioVascular Disease，ASCVD）的亚临床病理表现，进而导致缺血性卒中的发生［4-6］。颈动脉壁增厚与一些可改变的危险因素，如高血压、抽烟、饮酒和缺乏体育锻炼等有关［7］。因此，早期发现颈动脉异常不仅能够识别易患脑卒中的人群，而且通过预防干预也可以延缓和避免急性临床事件的发生。

在临床实践中，B 超是诊断和评估颈动脉异常包括CIMT、颈动脉斑块和颈动脉狭窄等的有效工具之一［8-9］。然而，受制于有限的医疗资源，颈动脉超声检查在大规模的脑卒中筛查中是耗时且昂贵的，特别是在欠发达国家和发展中国家的偏远地区。因此，有必要利用人工智能技术建立一种简单的基于生理检查和电子病历（Electronic Medical Record，EMR）的颈动脉异常早期识别方法，这不仅有助于早期筛查脑卒中，同时也能促进数字化医学的发展。现有的包括机器学习、深度学习等在内的人工智能技术都是以数据为基础的，因此，建立可靠的模型需要足够的、完整的数据集。然而医学数据的获取又是不易的，而且由于系统性、偶然性或是人为过失等缘故，数据总是不可避免会出现缺失。粗略地去除含有缺失值的数据将减少样本容量，并最终影响所建模型的效果。因此，如何处理缺失数据也是卫生信息学研究中另一个常见而又具有挑战性的问题。

本文以容易获得的个体体格信息、常规体检信息和家族病史作为特征属性，以颈动脉超声检查结果作为标签建立识别和预测异常颈动脉的模型，初步确定颈动脉病变，包括CIMT、颈动脉狭窄和斑块等颈动脉异常情况，进而辅助脑卒中的早期筛查。

K近邻（K-Nearest Neighbors，KNN），均值和众数常被用来填补缺失数据，而VAE 常用来生成新样本数据。为了处理缺失值，本文提出了两种缺失数据填补方法：一是KNN、均值和众数混合的方法（Mixture of mean，mode andKNN，MKNN）；二是改进的变分自编码器（Variational AutoEncoder，VAE），分别运用这两种方法对样本中含有的缺失值进行填补。利用遗传算法（Genetic Algorithm，GA）［10］对样本含有的属性特征进行筛选并结合逻辑回归（Logistic Regression，LR）［11］、支持向量机（Support Vector Machine，SVM）［12］、随机森林（Random Forest，RF）［13］和极限梯度提升树（eXtreme Gradient Boosting Tree，XGBT）［14］四种有监督学习方法建立异常颈动脉分类模型，评估MKNN和改进的VAE两种数据填补方法的效果。最后建立基于改进的VAE的半监督异常颈动脉预测模型。

本文的主要工作包括以下几个方面：

1）运用MKNN 以及改进的VAE 分别对含有缺失值的样本数据进行填补。

2）运用多种方法对特征进行分析并排序。

3）运用不同的分类方法结合GA 对缺失值填补前后的数据进行建模，发现基于改进的VAE的半监督模型性能最好。

1 相关工作

目前关于脑卒中的研究，大都致力于探寻卒中风险因子，或是对预后脑卒中发展情况进行预测。文献［7］基于统计学方法，通过线性回归系数来衡量与脑卒中关系密切的风险因素和疾病。文献［15-16］通过显著性检验、皮尔森相关系数等建立线性风险评分模型，预测干预后卒中的死亡和致残情况。在脑卒中的早期预测方面，文献［17］提出了Framingham 风险评分模型来预测未来10 年脑卒中发病风险，它是通过多年大量的研究，针对5 个危险因子建立的分层表。文献［18］中基于国内实际情况建立了心血管风险预测方法——China-PAR（Prediction for ASCVD Risk in China），这是一种预测10 年内脑卒中发病风险的模型，与国际上的Framingham 风险评分模型类似，不过它加入了体现中国人群脑卒中风险特征的因素，因此更适合预测中国人的情况。然而，这些方法都是基于数理统计方法建立的线性分析模型，未能很好地探索存在的非线性关系；并且预测的是10 年期的发病风险，时间范围太大。这些都将不同程度地影响模型的性能。

近年来，随着计算机技术的快速发展，机器学习方法越来越多地应用于疾病诊断和预测方面，如糖尿病的预测［19］、癌症的诊断和预测［20］、风湿病的研究［21］、慢性肝病的预测［22］等。2017 年，文献［23］指出机器学习算法相较于传统线性模型可以提高心血管疾病风险预测的准确性。随后，许多研究者致力于在机器学习方法如RF 和SVM 的基础上进行更准确的预测或分类。本文主要解决两个问题：一是缺失值的填补；二是利用容易获得的调查信息和体格检查，建立异常颈动脉识别和预测模型，间接达到大规模脑卒中初步筛查的目的。

2 本文方法

本章主要介绍缺失数据填补、特征排序、GA、有监督学习模型以及模型评估方法。重点阐述了改进的变分自编码器的原理和具体实现过程。

2.1 数据填补方法

2.1.1 MKNN

考虑到男性和女性不同的生理特征，对不同性别分别处理，过程如下：

1）将数据集按照性别分为两类，分别处理每一类。

2）对数据进行归一化，转化到区间［0，1］上。

3）对于腰围，根据身高和体重，采用KNN 来寻找最近值，然后填补，设置K=1。

4）对于连续变量，使用平均值来填充；对于离散变量，使用众数进行填补。

5）将处理后的两个类合并，作为填补所得数据集。

2.1.2 改进的VAE

文献［24］首次提出VAE，它是一种深层生成模型，基于的原理是：对于任意一个n维的随机变量X，总是可以用n个服从标准正态分布的随机变量Z通过一个足够复杂的函数去逼近它。该方法的分布可以表示为：

其中：P(X)为随机变量X的分布函数，P(Z)为标准正态分布，P（X|Z）为变量X的后验分布。根据这个后验分布进行采样，就能够得到与变量X类似的生成变量，即达到了数据生成的目的。P（X|Z）即可认为是上面提到的所谓的足够复杂的函数，它由称为解码器的神经网络计算所得。这种方法被广泛应用于图像、文本、视频和人机交互［25-27］等各个方面。该算法能够有效模拟大型高维度数据集的分布情况，生成与原始真实数据相似的新数据，但不能直接适用于混合有连续和离散值并且包含缺失值的数据。

文献［28］提出了一种可以处理异质（同时存在连续值和离散值）不完整数据的变分自编码器，它不仅能够处理连续值，而且也能够处理分类值、计数值和序数值等离散值，同时也能够补全不完整的数据。本文对该变分自编码器进行了优化，包括超参数的调整、dropout 层的使用以及目标函数的改进，结果表明改进的VAE 对于本实验的样本集效果更好。首先，由编码器构建一个混合高斯分布，代表离散值和连续值的后验概率分布；然后，据此采样两个隐变量；其次，由解码器假设两个先验分布，对于连续变量构建标准正态分布，对于离散变量构建均匀分布；同时，解码器还包括两个似然函数模型，这两个似然函数根据采样的隐变量产生与原始样本近似的生成样本。优化函数包括两个部分：一是重构误差，它度量了生成样本和原始样本之间的差异，用均方误差来计算；另一个是后验分布与先验分布之间的差异。用交叉熵（cross entropy）来度量离散变量分布之间的差异，用KL（Kullback-Leibler）散度［29］度量连续变量分布之间的差异。优化函数的计算不包括缺失部位的数据。具体设计步骤如下：

1）编码器构建在X条件下的高斯混合后验分布q（S|X）和q（Z|S，X），依此进行采样得到隐变量S和Z，并将之输入到解码器用来生成新样本。S代表独热编码向量空间，包含了混合高斯分布的均值和方差信息，Z代表隐变量空间，用来生成新数据。

2）解码器创建高斯混合先验分布p（S）和p（Z|S），并根据p（X，Z，S）采样生成新样本。对于连续数据，假设高斯似然分布p（X|Z）；对于分类数据，使用多项式p（x=r|Z）来表示每个类别的概率分布，r为离散值。H代表隐藏层的输出。

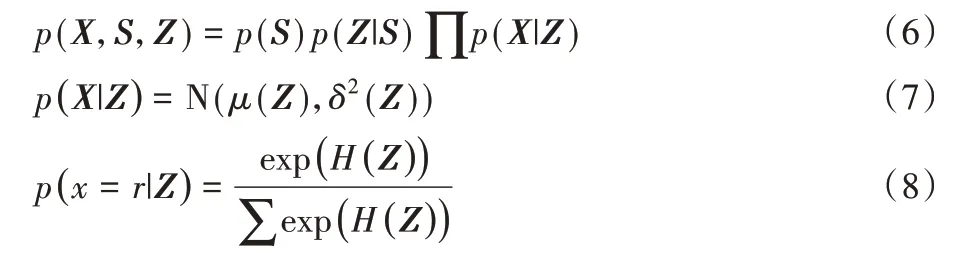
3）批处理数据归一化（Batch Normalization，BN）和逆归一化（Batch De-Normalization，B-DN），防止某些特征主导训练过程，并防止KL散度消失。dropout层用来避免过拟合。

4）优化函数下界（Evidence Lower BOund，ELBO），优化编码器和解码器的参数。KL(·)表示KL 散度计算公式，EN(·)代表交叉熵计算公式，a、b∈［0，1］，代表权重系数。本文设置a=1，b=0.5。

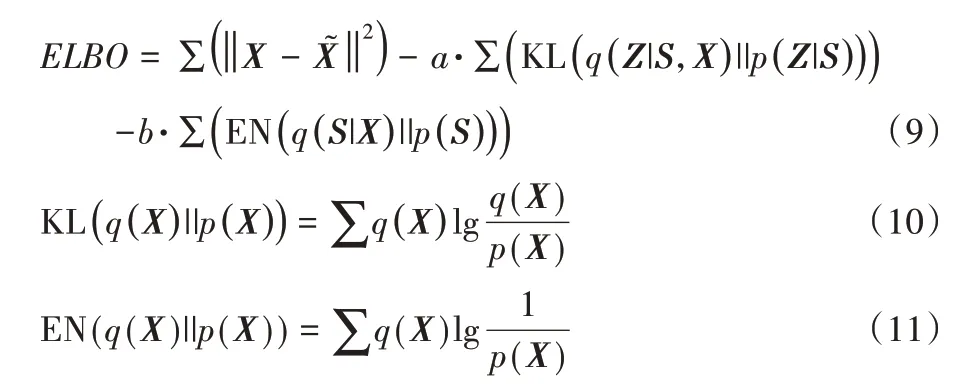
图1 展示了改进的VAE 模型的流程。N1 是一个创建离散分布的全连接深度神经网络和BN 层；Sm是一个采样的独热编码向量；N2 是一个神经网络和dropout 层，产生均值和方差来创建一个产生潜在变量的高斯分布；Zm是采样所得的隐向量，并服从标准高斯分布；N3 是一个创建高斯先验分布的softmax层；L-hood是生成新样本的似然函数层，它可以生成连续值和离散值；N4 是B-DN 层，将数据返回到原始的数值范围；Input 是输入的数据集；Output 为改进的VAE 生成的新数据集。

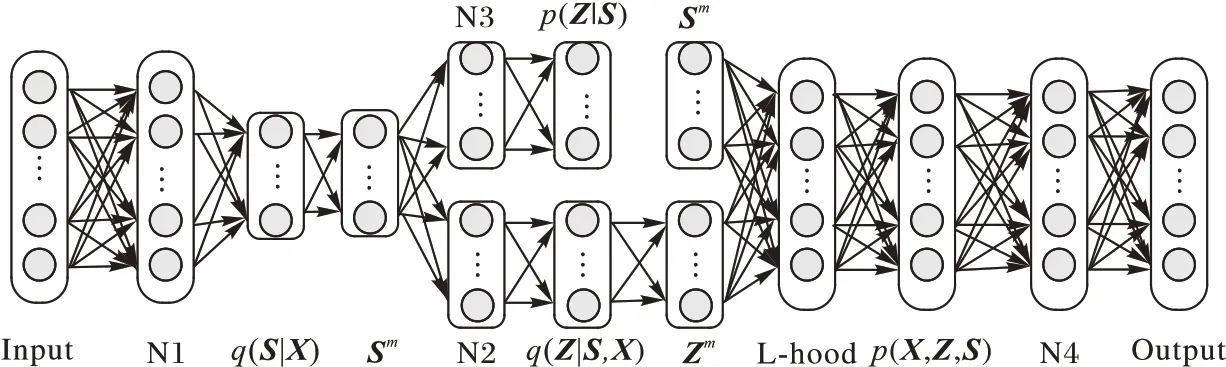
图1 改进的VAE的流程Fig.1 Flowchart of improved VAE

2.2 遗传算法

GA是一种通过模拟自然进化过程来搜索最优解的方法，它被广泛应用于路径优化、最优值查找和特征筛选［30-31］等方面。本文用GA来进行特征选择。具体如下：

1）初始化。设置最大进化次数T和初始群体S（0），S（0）包括若干个体，每个个体具有不同的染色体。在本文中，染色体长度设为L，代表不同的基因（特征属性），用长度为L的一维数组来表示，数组只包含0 和1，0 代表不含有该位置的特征，1表示含有该对应位置的特征。

2）计算适应度。计算群体S(t)中每个个体的适应度。本文中，每个个体代表一个特征集合，对仅包含这个特征集合的数据集进行建模，以模型5 折交叉验证的分类准确率作为每个个体（所选特征）的适应度值。

3）遗传。将适应度高的个体遗传到下一代。本文以轮盘赌的方式在群体中选择个体进行遗传，将适应度高的特征集合保留下来。适应度越高，个体保留下来的概率也越高。

4）交叉。在群体中对染色体进行交叉，实现特征集合的变化。本文每两个染色体进行部分交换，以［0，1］上的随机数模拟概率，当满足交叉概率Pc时，在某个点位处将两个染色体的后半部分交换，否则不进行交叉。

5）变异。对群体中每个染色体进行基因突变，实现特征集合的改变。本文中，当满足变异概率Pm时，在某个点位进行突变，即原来的1变为0，原来的0变为1；否则不发生突变。

6）判断。满足条件终止计算，并输出具有最大适应度的个体。当不满足终止条件时，依次重复步骤2）～6）。本文中，当进化次数超过T时，算法终止。

2.3 有监督学习

LR、SVM、RF 和XGBT 是在医学、经济和环境等许多领域广泛应用于分类和预测任务的有监督机器学习算法。

1）LR 是一个广义线性模型，是在线性回归的基础上加入了非线性（sigmoid 函数）映射，与线性回归不同的是，LR 输出的是离散值，所以解决的是分类问题。

2）SVM是一种二分类模型。它首先定义一个在特征空间上间隔最大的线性分类器，当数据线性不可分时，先利用核函数将特征空间的数据进行映射，再求解能够正确划分训练数据集并且使得几何间隔最大的超平面，所以SVM 是一种非线性分类器。

3）RF 是一种集成学习模型，是为了解决单个决策树模型的不足，从而整合起更多的决策树来避免局限性。对于分类问题，整合每一棵树的结果进行投票。首先对样本和特征同时进行有放回随机采样，生成若干个训练集；然后对每个训练集构造一棵决策树；最后整合所有树的结果，输出模型分类结果。由于同时对样本和特征进行了采样，所以RF可以很好地避免过拟合。

4）XGBT 也是一种集成学习模型，它也是整合若干个弱学习器的结果，然后输出最终的结果。不同于RF 的是，这些弱学习器是依次建立的。首先，定义损失函数；然后，基于损失函数的负梯度进行学习，也称为基于伪残差的学习。在具体实现时，XGBT 对损失函数进行二阶泰勒展开，以一阶导数，二阶导数和正则化来训练回归树，迭代生成若干个基学习器，相加输出分类结果。

2.4 评估指标

本文采用的是平衡数据集，即正样本（标签为1）和负样本（标签为0）数量相同。定义混淆矩阵：正样本被预测为正样本的数量（True Positive，TP），正样本被预测为负样本的数量（False Negative，FN），负样本被预测为正样本的数量（False positive，FP），负样本被预测为负样本的数量（True Negative，TN）。为了评估分类模型性能，采用如下指标：

1）灵敏度（Sensitivity，Sen），反映了对正样本的识别能力，值越高，说明模型越能够识别出患病的样本，漏诊的概率就越低。计算公式为：

2）特异性（Specificity，Spe），反映了对负样本的识别能力，值越高，说明模型将负样本识别为正样本的概率越小，误诊的概率就越低。计算公式为：

3）F1 值，是精确率P和召回率R的调和平均值，它也是衡量模型性能的一个重要指标。计算公式为：

4）分类准确率（Accuracy，Acc），准确率越高，说明模型预测的越准确。计算公式为：

运用皮尔森系数（Pearson）的绝对值分析特征与目标之间的线性关系。皮尔森相关系数定义为：

利用最大互信息系数（Maximum Mutual Information，MIC）［32］度量特征与目标之间的非线性关系。最大互信息系数定义为：

其中：|X|、|Y|表示对数据进行网格化处理时的分段个数；B为划分方格总数的限定值，可根据实际情况进行设定。

3 实验和结果分析

3.1 实验数据

数据来源于深圳市第二人民医院脑卒中筛查与预防项目（伦理审批号：20200116002）。受试者为年龄超过40 岁的本地居民，共入组2 626名，建立了含有缺失值的原始数据集，包括34 项特征和1 项标签，缺失数据分布情况如表1 所示。34个特征说明如表2 所示。同时，通过去除含有缺失值的样本，得到另一组数据集（完整数据集），共2 049个样本。这些特征属性包括问卷调查、实验室检查和体格检查。另外，本文将颈动脉超声检查结果作为分类目标：颈动脉正常（标签0）和异常（标签1）。颈动脉超声检查结果异常包括CIMT、颈动脉狭窄或出现斑块；相反，检查结果正常代表颈动脉无异常。为了避免数据不平衡问题，随机选取最大数量的正常样本，得到两个平衡数据集Dx和Dc。Dc不含缺失数据，Dx包含缺失数据，且每个样本缺失值个数不超过5。使用MKNN 和改进的VAE对数据集Dx 分别进行填补，得到两个完整的数据集Dm 和Dv，如图2所示。

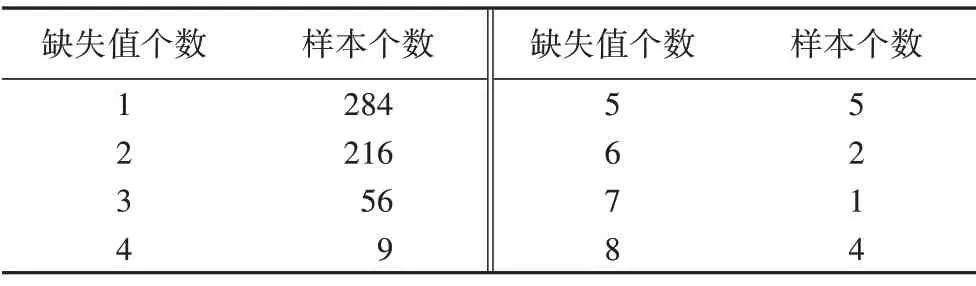
表1 缺失值分布情况Tab.1 Distribution of missing value

表2 特征变量说明Tab.2 Description of feature variables

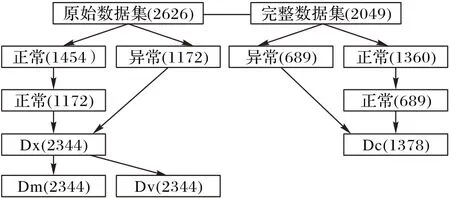
图2 数据处理过程Fig.2 Data processing process

图2显示了数据的处理过程。其中使用改进的VAE的具体步骤为：先对含有缺失值的数据集进行预填充，即用每个对应属性中已经出现的任意一个数值来填充缺失部位的值，得到预填补后的数据集，这样做仅仅是为了能够进行数学计算；再将预填充的数据集作为改进的VAE 的输入（Input），经过处理得到输出（Output）；然后保持原始数据集中真实数值不变，用Output中的数据填补缺失值，即得到填补后的数据集。

3.2 实验设置

所有实验均在一台本地工作站（Intel Core I5-6500 CPU 3.20 GHz，内存20 GB）上操作运行。用Python3.7 来处理数据集，并进行模型建立和分析。VAE 部分，使用Tensorflow 框架来建立深度学习模型。

数据集按照7∶3 的比例划分为训练集和测试集，并保证训练集和测试集的正负样本数量保持平衡。模型建立之前先对特征作归一化处理，以免因数据范围的不同而影响模型的性能。每个实验重复5次，得到平均结果。

本文首先进行特征分析的实验，对特征进行排序；接着对数据集Dc、Dm 和Dv 分别运用遗传算法进行特征筛选并建立有监督模型，以此评估数据填补方法的性能；然后，建立半监督模型；最后，对比所有模型结果。设置遗传算法L=34，Pc=0.6，Pm=0.2，T=300。

3.3 实验结果

利用Pearson、MIC、递推特 征消除（Recursive Feature Elimination，RFE）法、RF 与XGBT 内置的属性重要度法来确定所有特征的重要性，每种方法都将结果归一化到区间［0，1］。综合这6 种分析的结果，对特征进行排序。考虑到结果的可靠性，本文对不含缺失值的数据集Dc进行特征分析，图3显示了特征排序的结果，LR_REF 和SVM_REF 表示基于LR和SVM 建模的递推特征消除法。可以看出，不同的方法得到的结果具有很大程度的一致性，这说明所得的特征排序能够反映特征与目标之间的关系。腰围、年龄、卒中家族史、脉压、同型半胱氨酸等特征的重要性比较高，表明它们与颈动脉异常的发生关系密切，也暗示着脑卒中的风险。

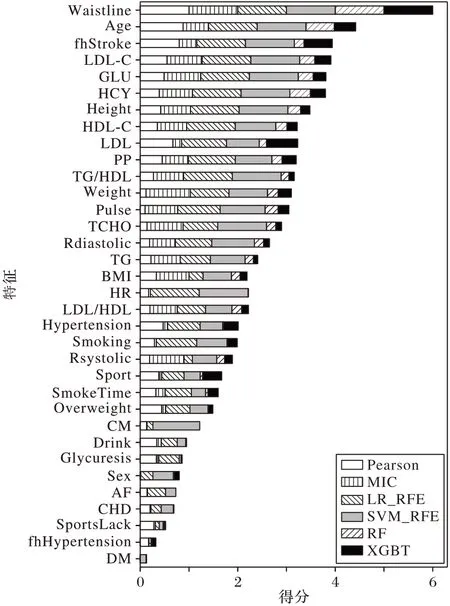
图3 特征排序Fig.3 Feature rank

3.3.1 监督模型性能

为了评估MKNN 和改进的VAE 两种方法填补缺失值的效果，采用LR、SVM、RF和XGBT 这四种有监督学习方法结合GA分别对Dc、Dm 和Dv建立分类模型，其中基于数据集Dc所建的模型作为本实验的基线模型。表3 显示了各个模型的性能指标，从中可以得出三个方面的结果：

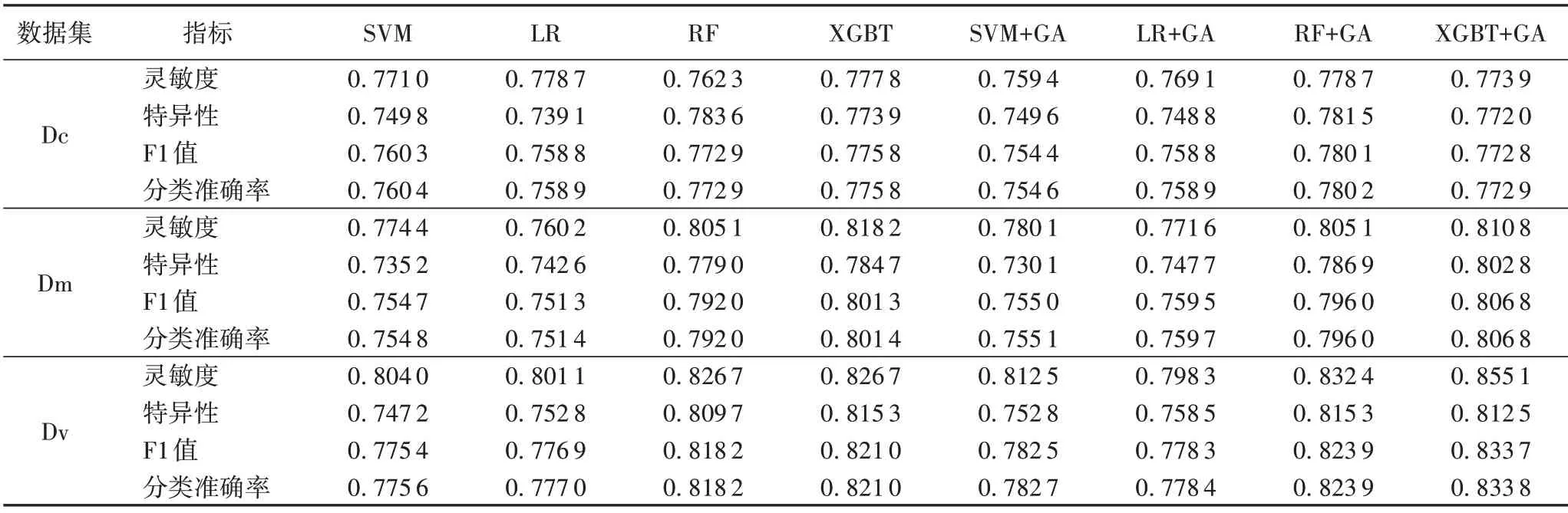
表3 不同模型的各项指标对比Tab.3 Comparison of indices of different models

1）对于用同种方法填补所得的数据集，不论是否进行特征筛选，集成方法XGBT 明显取得了最好的效果，集成方法RF在测试数据集上也取得了良好的结果；而在以往的大多数分类任务中被广泛使用的LR 和SVM 模型，表现并不好。这说明，常见的监督模型中，XGBT 模型更加适合用来对本文的数据进行建模。

2）对于不同数据集，不论是否进行特征筛选，使用同种方法进行建模时，基于Dm 所得模型准确率与Dc 的模型相当或是提高2%左右；基于Dv 所得模型准确率与Dc 的模型相比提高1%～4%；基于数据集Dv 构建的分类模型的各项指标均比对应的由Dm 建立的模型提高2%以上。这说明对本实验数据集而言，MKNN和改进的VAE都是不错的数据填补方法；而对于两种填补方法而言，改进的VAE的性能明显优于MKNN，这表明改进的VAE是一种填补缺失值的更好方法。

3）对比特征筛选前后的模型，可以发现运用GA 进行特征筛选后模型各项指标都有所提升。这说明，使用GA 进行特征筛选是得当的，得到更少的特征数量，使得模型复杂度降低，同时也使得模型性能得到提升。

由于本文使用的是正负样本数量相同的平衡数据集，所以对于每单个模型可以发现它的F1值和准确率是相等的。

对于数据集Dv，在XGBT 模型中，GA 筛选出了24 个特征。它们编号分别为（1，2，3，4，5，7，8，9，10，11，13，14，16，17，18，20，22，23，25，27，28，32，33，34），参考表2。

3.3.2 基于改进的变分自编码器的半监督模型性能

由3.3.1 节知，改进的VAE 是一种能够填补不完全数据的较好的方法。考虑到它可以填补类型为离散值的特征，本文设想它也可以处理目标中的值。基于此思想，建立了一个分类模型。具体过程如下：首先隐藏一些标签，将目标值转换为含有缺失值的数据；然后利用改进的VAE 对不完整数据进行估计；再将估算的标签值与真实值进行比较，并计算敏感度、特异性、F1 值和准确率。同时参考3.3.1 节，为了方便对比，也使用XGBT 模型中运用的24 个特征。随机删除30%的标签来训练生成模型，这意味着训练集和测试集的比例为7∶3。重复5次实验，取平均结果，见表4。

表4 不同模型的结果对比Tab.4 Comparison of results of different models

表4 实验结果表明，将特征进行筛选之后，使用基于改进的VAE 的分类方法所建立的模型各个分类指标都有了明显的提升。同时，对比表2 和表3 的结果，发现基于改进的VAE+GA 的方法（敏感性为0.893 8，特异性为0.927 2，F1 值为0.910 5，准确性为0.910 5）在所有指标中均获得最佳结果。与常用的监督模型相比，此方法所得模型各项指标都提高了6%以上，同时对比本文的基线（基于平衡的完整数据集Dc 所建模型），可以发现基于改进的VAE+GA 的半监督模型性能提升明显。

4 结语

利用医疗数据，本文提出基于改进的变分自编码器的半监督模型来识别和预测异常颈动脉，进而间接达到脑卒中大规模初步筛查的目的。它是一种简单的分类模型，仅仅依靠常规的体检和家族病史信息；同时该方法还能够填补丢失的数据，使得数据集可以在更广泛的分类算法中得以运用。另外，分析了每个特征属性与目标值之间的关联，尤其是筛选出来的24 个使得模型效果最好的特征属性，可以在日常生活中重点关注，这对预防和风险控制提供了参考。

在未来的工作中，我们可能会收集更多的样本和特征属性来建立更有说服力的模型；对特征属性进行更为细致的分析和筛选，在探究特征属性与卒中的关系的同时，使得模型更加简洁；此外，筛选一部分年龄不太大的个体，对其进行长期跟踪，以此来评估和改进提出的模型。同时，本文提出的半监督模型也可以转化为安装在移动设备上的应用程序，用于脑卒中的早期自我筛查。