变运行参数的磁性液体密封中磁液温度特性分析*

李望旭 李正贵 袁久越 颜招强

(1.流体及动力机械教育部重点实验室(西华大学) 四川成都 610039；2.自贡兆强密封制品实业有限公司 四川自贡 643000)

在诸多工业领域，密封问题是工业技术上的一大难题，尤其在一些精密仪器和医疗设备的密封问题上，不容出现任何差错。目前传统密封方式存在易膨胀溶解、易磨损、易老化等缺点[1]，密封可靠性不高，因此急需一种新的密封方式来代替传统密封。

自20世纪60年代美国航天局率先将磁性液体密封技术应用在宇航服可动部分的真空密封后，磁性液体密封技术受到科研人员的广泛关注[2]。磁性液体密封的密封原理是通过永磁铁(或电磁铁)产生磁场，磁性液体对磁场作出响应，紧紧吸附在密封间隙中，形成“O”形密封圈[3]，实现密封效果。因磁液可充满整个密封间隙[4]，且密封不依靠外界物质(仅依靠由磁铁产生的磁场)，故在密封上有“零”泄漏[5]、易维护[6]、可靠性强、寿命长等优点[7-8]。但同时其也存在密封压差小、温度适应性差的缺点。为此国内外学者针对磁性液体密封技术进行了深入探索。

磁性液体密封的长寿命和高可靠性是以工作环境稳定且适当为前提。磁性液体由磁性颗粒、表面活性物和基载液组成[17]，包裹了磁性颗粒的表面活性物质弥散在基载液中，大大增加了磁液黏度，在进行气体或真空旋转密封时，磁液在主轴带动下转动，因黏滞力产热，导致磁性液体温度上升[18]。当温度高于磁液限制温度时[16]，基载液中的磁性颗粒将聚集在一起，形成凝聚体，破坏磁液本身的稳定性，降低密封效果[19]；其次，磁性液体基载液会汽化，造成磁液体积量减小，严重时导致磁液“干涸”，致使密封失效。因此，为保证磁性液体密封的可靠性和长寿命，对磁性液体旋转密封时磁液温度和磁液蒸发时气相分布状态的研究十分必要。

本文作者通过数值计算与试验验证相结合的方法，对磁性液体旋转密封的温度、相变现象与轴径、转速之间的关系进行了研究，为设计磁性液体旋转密封结构提供理论参考。

1 理论分析

磁性液体在旋转动密封时，主轴带动磁液旋转，磁液的黏滞力产生黏度热效应，导致磁性液体温度升高[20]。温升计算公式为

(1)

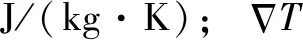
在流体中，热传递的方式主要有热对流和热传导，由于间隙中磁性液体体积较小，热对流可以忽略，故密封装置内部热传导起绝对作用。文中研究的是三维圆柱模型，因此采用柱坐标系的导热微分方程[20]:

(2)

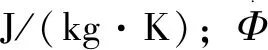
导热系数的定义式由傅里叶定律的数学表达式可以得出[20]：

(3)

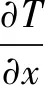
磁性液体密封装置的壳体向外散热过程主要是对流传热，对流传热的基本公式[20]为

q=h(Tw-Tf)

(4)

式中：h为表面传热系数，W/(m2·K);Tw为壁面温度，K；Tf为流体温度，K。

磁性液体黏度与磁场强度和温度有关[21],根据现有研究结果，磁性液体黏度随温度升高而降低，并有如下关系式[21]：

η=e-0.042 2T+15.746T>270 K

(5)

式中：η为磁性液体的黏度，mPa·s；T为磁性液体的温度，K。

磁性液体黏度与磁场之间的关系[15]为

η=4.615 8-0.006 4B+0.001 7B2

(6)

式中：B为磁感应强度，T。

磁性液体在密封间隙处运动应遵循质量守恒方程[18]：

(7)

式中：ρf为磁性液体的密度，kg/m3；ux、uy、uz分别为磁性液体沿x、y、z方向的速度。

2 数值模型

由于磁性液体黏度与磁场强度、温度有关，故需要分别对磁性液体密封装置的磁场、流场和温度场进行计算。

磁场通过Maxwell进行数值计算，磁性液体密封结构由主轴、磁性液体、极靴、永磁体组成(如图1所示)，永磁体轴向充磁，边界条件为狄里克莱。极靴和转轴的材料均采用Steel-1008材料，该材料的B-H曲线如图2所示，永磁铁采用NdFe30,剩余磁通密度Br为1.2 T,矫顽力Hc为8.38×105A/m，由于磁性液体密封为旋转结构，因此可将模型简化为2D轴对称模型。

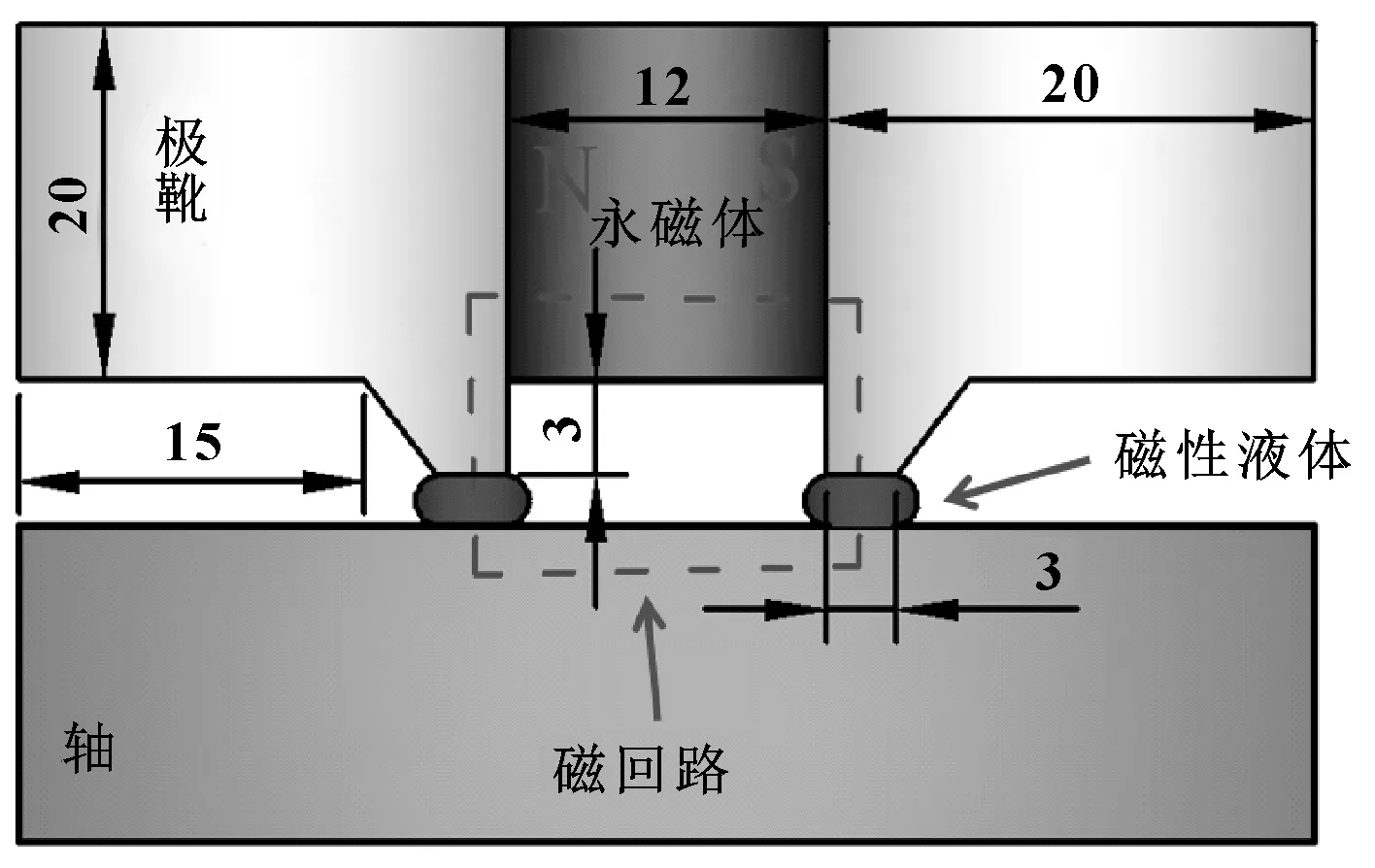
图1 密封结构示意Fig 1 Schematic of the sealing structure

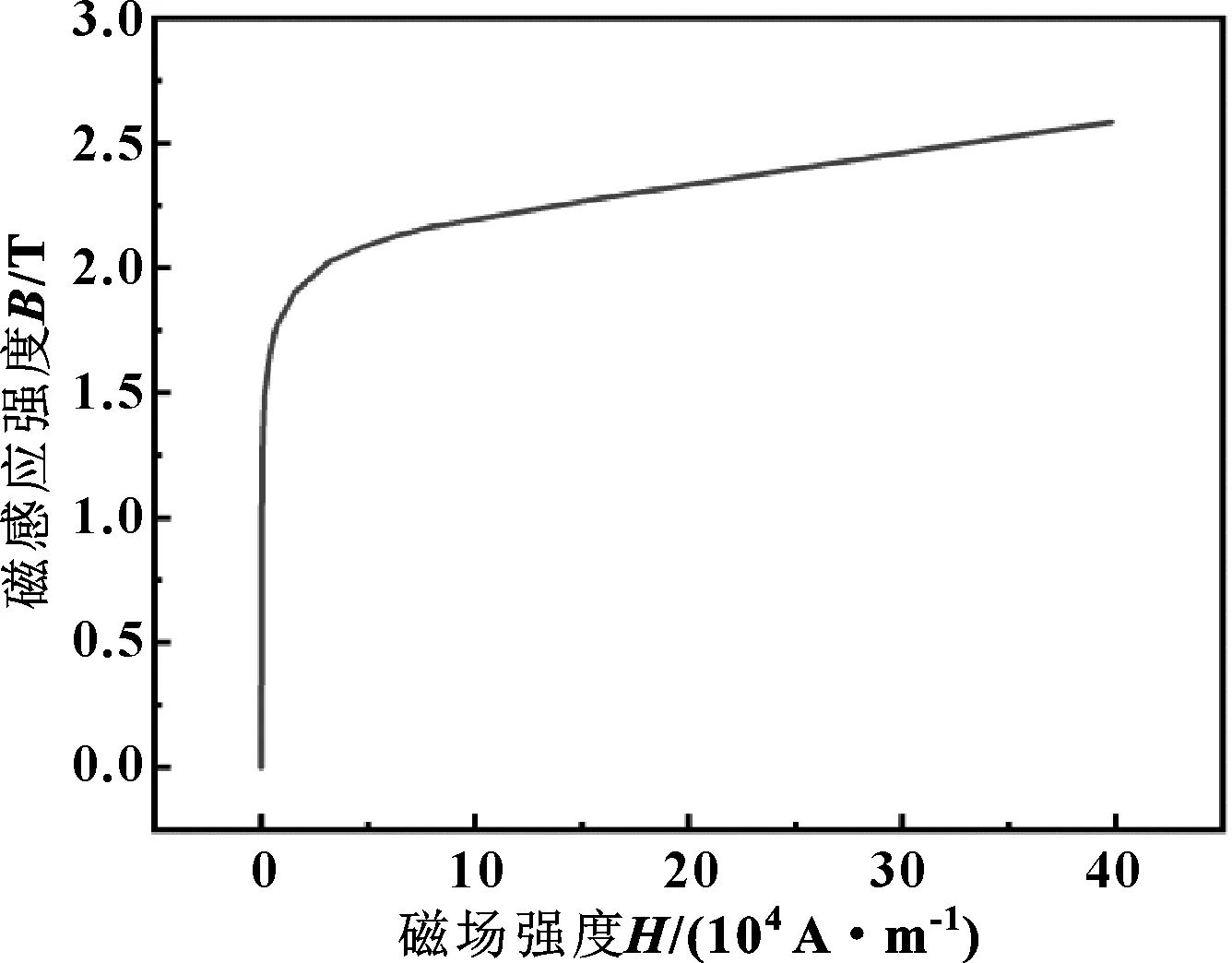
图2 Steel-1008材料B-H曲线Fig 2 B-H curve of Steel-1008 material

根据计算出来的磁场结果，由公式(6)得出与之对应的磁液黏度，作为磁液初始黏度。通过Fluent对磁液旋转密封时的温度场进行计算，指定与磁液接触的轴表面运动方式为旋转，轴径选取50、100、200 mm，转速分别为100、200、300、40、500、700和1 000 r/min，并将磁液黏度与温度的关系通过UDF(User Define Function)进行定义，UDF程序如下所示：

#include"udf.h"

DEFINE_PROPERTY(cell_viscosity,c,T)

#define e 2.71828

{

real mu_lam;

real temp=C_T(c,T);

mu_lam=pow(e,-0.0422*temp+15.746);

return mu_lam;

}

图3所示为温度计算模型，密封装置的外界温度为293 K，装置外表面和轴表面的传热方式为自然对流，自然对流系数取4 W/(m2·K)。磁液与极靴通过热传导的方式传递热量。磁液密度设为1.3 g/cm3,黏度由公式(6)推导得出。

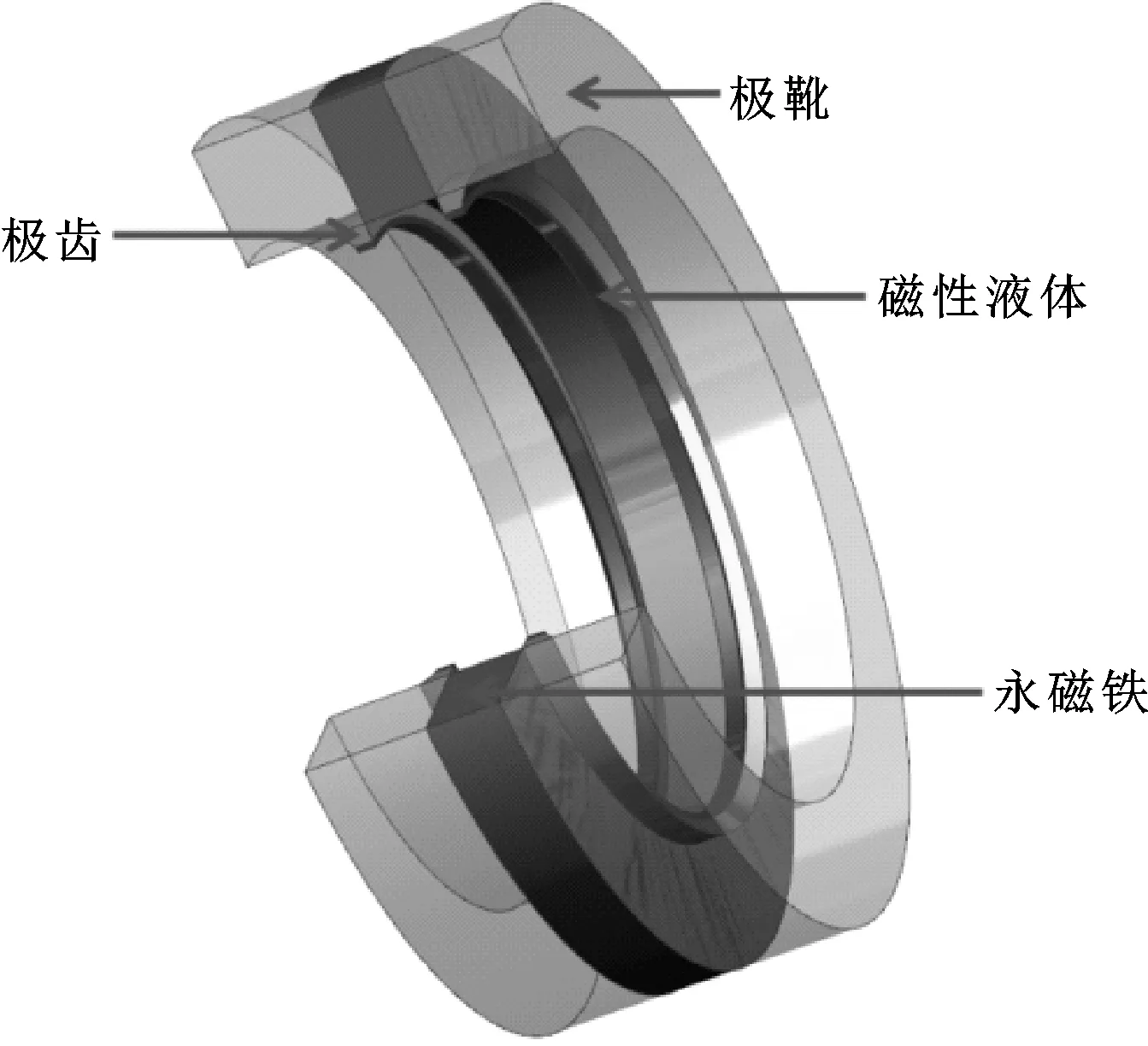
图3 模型示意Fig 3 Schematic of the model

文中研究涉及到黏性产热和传热计算，需开启能量方程和黏度热效应方程，流动模型选择层流模型，流体域与固体域为交界面耦合传热。

3 结果及分析

3.1 磁性液体密封装置的磁场分析

由图4可知，密封装置的磁感应强度以磁铁中心成对称分布，由于极齿处横截面积较小，而磁通量在磁场闭合回路中遵循守恒定律，故极齿处磁感应强度最大。极齿与主轴之间通过磁性液体作为介质构成磁路，磁性液体的相对磁导率与空气相近，远小于碳钢的相对磁导率，所以该处磁阻突增，导致磁感应强度下降。为得到磁性液体所在位置处的磁感应强度，对极齿底端至轴表面处做了5条监测线。

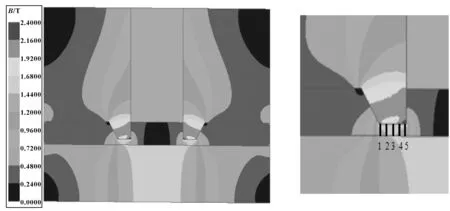
图4 密封装置的磁感应强度分布云图Fig 4 Magnetic induction intensity distribution cloud diagram of the sealing device

图5所示为极齿下端至轴表面处磁感应强度分布曲线。可知，除极齿边缘处磁感应强度沿径向下降明显外，其余部分的磁感应强度无明显下降趋势，而磁液主要集中在极齿底部，极齿边缘处只有少量磁性液体分布，故磁液黏度主要受极齿底部的磁感应强度影响。为简化计算，取监测线2、3、4的磁感应强度的平均值作为密封间隙处磁感应强度大小，并根据该值计算与之对应的磁液黏度。经计算得，密封间隙处磁感应强度为1.46 T，与之对应的磁液黏度为4.6 mPa·s。

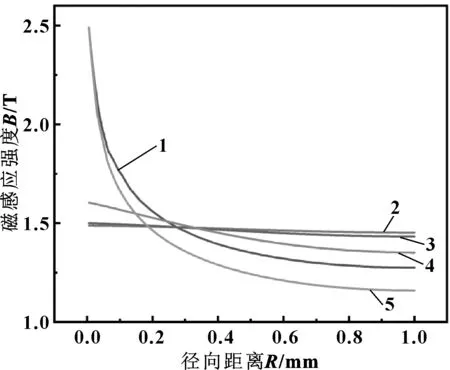
图5 极齿下端至轴表面处磁感应强度分布曲线Fig 5 Distribution curves of magnetic induction intensity from the lower end of pole tooth to shaft surface

3.2 磁性液体温度与轴径及转速的关系

图6所示为轴径100 mm时，不同转速下磁性液体温度分布云图。可知，磁液在主轴转动的带动下，因黏滞力产热而造成温升，当转速恒定时，因靠近轴表面处磁性液体的速度与轴速相近，而紧贴极齿底端的磁液速度趋于0，造成密封间隙处磁液的速度梯度较大，且速度梯度的量值沿径向递减。由牛顿内摩擦定律可知，黏滞力与速度梯度成正比，因此磁液温度最大值出现在与轴表面相接触的位置，最小值出现在与极齿底部相接触的位置。

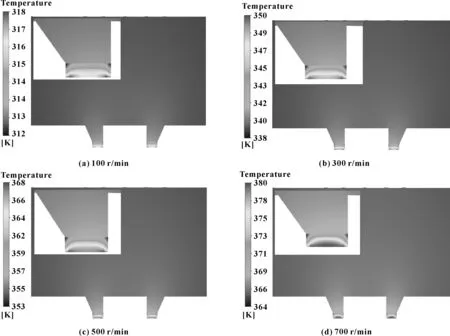
图6 轴径100 mm时，不同转速下磁性液体温度分布云图Fig 6 Cloud diagram of temperature distribution of magnetic liquid at different rotating speeds when the axle diameter is 100 mm(a) 100 r/min;(b) 300 r/min;(c) 500 r/min;(d) 700 r/min

当主轴转速增大时，磁液速度梯度增大，因此磁液温度最大值随转速增大而升高。当转速为100、300、500、700 r/min时，磁性液体的最高温度分别为318、350、368、380 K，由此可见，每提高200 r/min的转速，磁性液体最高温度的上升幅值逐渐减小。转速升高，磁液黏滞力所产生的热量增加，磁性液体密封装置的整体温度升高，导致与外界交换热量的速度加快，且温度升高后磁液黏度有所下降，产热率下降，故出现随转速升高，温升梯度量值递减这一现象。

磁液的工作温度不得超过343.15 K，温度过高不仅会造成基载液中的磁性颗粒聚集在一起，形成凝聚体，破坏磁液本身的稳定性，同时磁液还会发生相变，导致磁液体积量减小，降低密封效果。故当轴径为100 mm，转速为300 r/min时，若想磁性液体处于长期稳定的工作环境，必须施加冷却措施。

图7所示为不同轴径时磁液最高温度与转速关系。可知，转速为常量时，磁性液体的最高温度随轴径的增大而升高，且不同轴径时，磁液最高温度与转速的关系均呈现为指数函数关系。

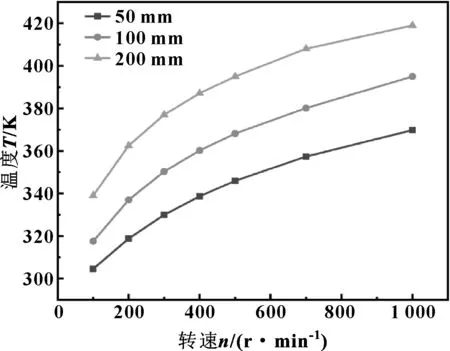
图7 不同轴径下磁性液体最高温度与转速的关系Fig 7 Relationship between maximum temperature of magnetic liquid and rotational speed at different axle diameter

表1给出了不同结构密封在不同运行参数下磁液最高温度的上升幅值。将表1中数据绘制成等高线图，如图8所示。可知，当两工况的轴径与转速乘积相等时，其温升幅度大致相等。由此可推断，磁性液体温升与轴径和转速的乘积有关，即与轴表面线速度有关。根据表1，以轴径与转速的乘积为x，温升幅度为y值，进行函数拟合，得到如下关系：

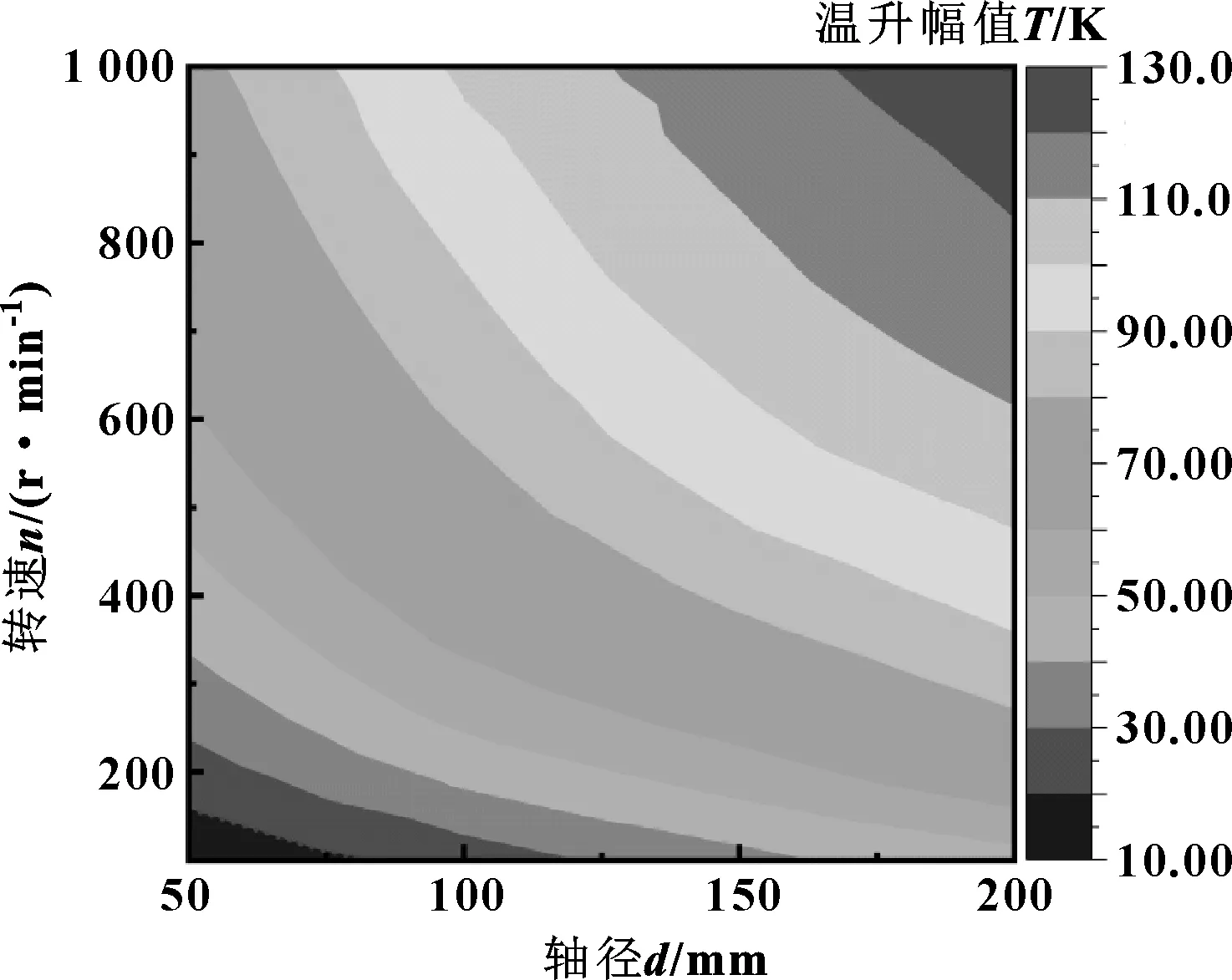
图8 磁温等高线Fig 8 Magnetic temperature contours

表1 不同工况下磁性液体温升Table 1 Temperature rise of magnetic liquid under different working conditions

y=119.327×(1-e-0.002 54x/119.327)

(8)

理论上，旋转设备因摩擦或黏性产热的速率应与线速度成正比，而当轴径增大时，散热面积也会同时增大，这将导致当两工况下轴径与转速乘积相等时，大轴径最高温度应该小于小轴径最高温度。而在磁性液体的旋转密封中，由于磁性液体黏度会因温度升高而降低，导致产热速率有所下降，其中小轴径产热速率下降的量值恰好与大轴径增大散热速率的量值相等，因此存在当轴径与转速乘积相等时，磁性液体温升相同这一规律。

3.3 磁性液体相变与轴径的关系

当磁液的温度高于工作温度时，磁液会发生相变，造成磁液体积量减小，影响密封稳定。由前文已得出的结论：当轴径与转速的乘积相等时，磁液温升相同。为观察同一温升时，磁液蒸发的气相分布状态与轴径的关系，以轴径50 mm、转速500 r/min的最高温度359.9 K为基准值，通过上述定理，可以得出轴径100 mm、转速250 r/min和轴径 200 mm、转速125 r/min时的最高温度同样为359.9 K，故在进行气相分布研究时，轴径为100、200 mm时分别取转速为250、125 r/min。

以上述每个工况的稳态值为初始结果，进行mixture瞬态计算，将相变温度设置在343.15 K，图9所示为计算1 s时的气相分布云图。

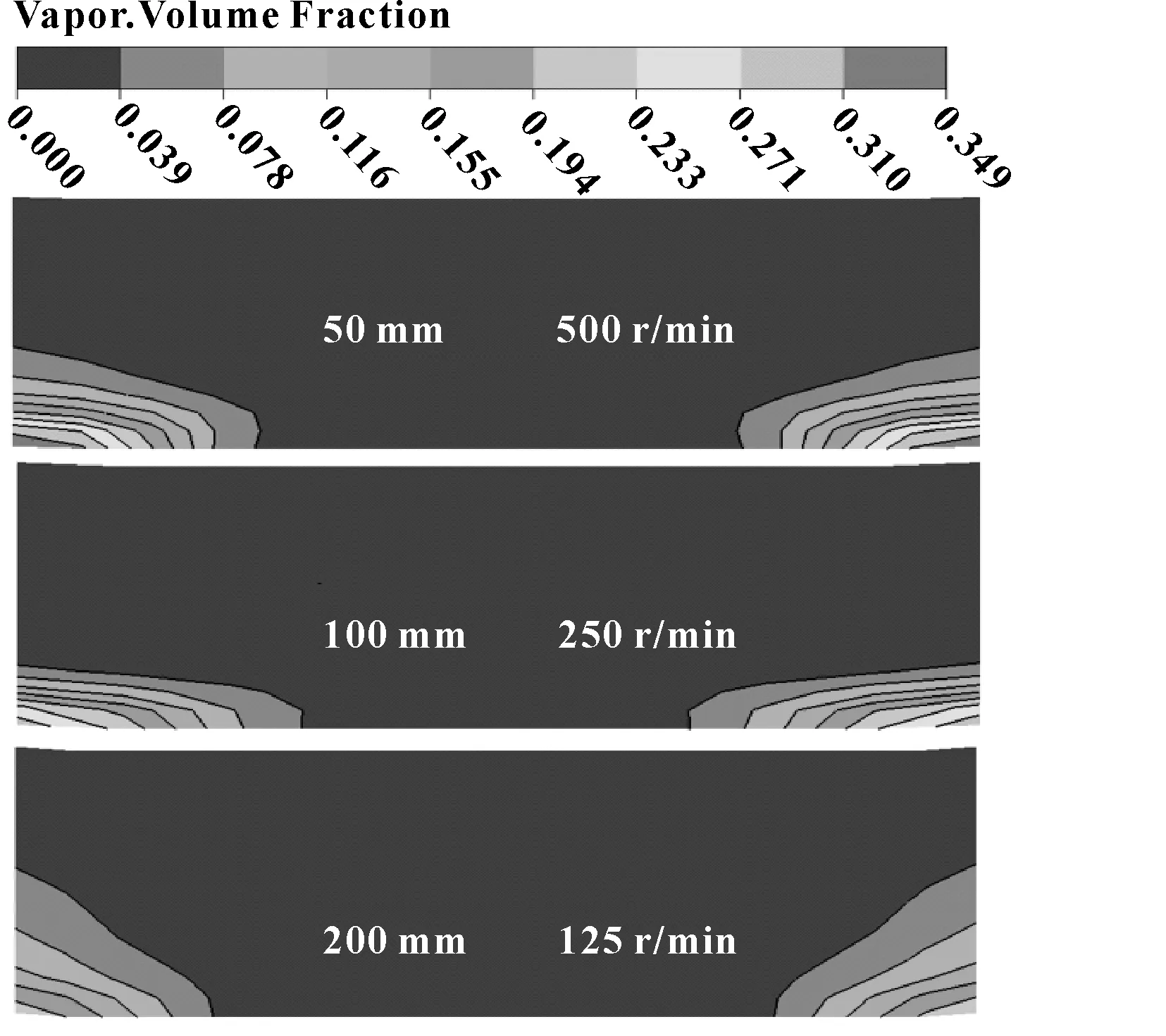
图9 磁性液体气相分布云图Fig 9 Gas phase distribution nephogram of magnetic liquid

如图9所示，不同轴径下，磁液发生汽化的初始部位均在与外界环境相连通的轴表面处，且以抛物线的形式逐渐向内部扩散。在工作温度相同时，随轴径增大，磁液汽化的体积分数下降，这是由于当轴径增大后，磁液本身的体积也相应增加，而汽化需要吸收热量，导致磁液周围温度略微下降，故气相体积分数相应减小。由此可知，在设计磁性液体旋转密封装置时，磁液与外界相通且靠近轴面处的冷却措施应着重考虑。

4 试验验证

为验证数值计算的准确性，对磁性液体旋转密封气体时的磁液温度进行了试验研究，试验在高温磁流体密封试验台上进行，如图10所示。该试验装置为轴径100 mm的磁性液体密封装置，可通过控制系统对电机转速进行控制，实现转速的随意调控，并可通过气压设备施加进口压力。该设备通过电机带动主轴转动，使磁液运动，进行黏性产热，通过温度传感器将监测的温度数据实时传送至控制台。不同转速下的试验结果如表2所示。可见，试验结果与仿真结果基本相符，验证了数值计算的准确性。由于试验台中磁液密封装置外部还设有保护层，阻碍了散热，导致试验结果比仿真结果略偏大。

图10 高温磁流体密封试验台及测控系统Fig 10 High temperature magnetic fluid seal test bed and measurement and control system

表2 不同工况下计算值与试验值对比Table 2 Comparison of calculated values and experimental values at different

5 结论

(1)磁性液体旋转密封工作时，因黏性产热所造成磁性液体的温升，其温度最大值出现在与轴表面相接触的位置，最小值出现在与极齿底部相接触的位置。

(2)磁液温度最大值随转速增大而升高，但温度上升幅值随转速提高逐渐减小；磁性液体的最高温度随轴径的增大而升高。

(3)磁性液体的最高温度与轴表面线速度有关，当两工况轴径与转速乘积相等时，磁性液体的温升值相同。

(4) 当磁性液体温度高于其汽化温度时，与外界相通靠近轴表面附近的磁性液体最先发生相变，且相变面积呈现抛物线形状向内扩散。且相同工作温度下，磁性液体的相变体积分数随轴径增大而降低。