基于热弹流体动力混合润滑的船舶柴油机主轴承摩擦研究*

魏立队 曹 辰张登攀 李精明

(1.上海海事大学商船学院 上海 201306；2.上海海事局 上海 200086)

大型船舶柴油机的主轴承是其关键部件，近年来故障频发，严重影响整个柴油机工作的可靠性、安全性和经济性。尽管研究人员对内燃机主轴承已经做了大量研究工作，但受建模复杂度、计算成本等各种条件的限制，多数都是基于单个轴承座，或计入温度影响但不考虑轴颈和轴瓦变形，运用THD (thermal-hydrodynamic，简称THD)[1]方法进行计算；或考虑弹性变形但不计入温度影响，运用EHD(elasto-hydrodynamic，简称EHD)方法进行研究[2-3]，或计入温度影响，运用热弹性流体动力 (thermal elasto-hydrodynamic，简称TEHD)润滑方法[4-5]进行研究。这些模型没有将机体作为一个整体来考虑其与各气缸间、各轴承间的相互影响，计算结果与实际工况差异较大。即使有文献基于整个机体进行了研究，但有的文献忽略温度对油膜黏度和柔性机体及曲轴热弹变形的影响[6-8]，即采用EHD计算模型；有的文献计及温度影响，但忽略轴瓦和轴颈表面粗糙接触的影响，将工况理想化为全液动润滑[9-10]。这与大型船用柴油机主轴承重载、变工况的实际情况差异较大，当然也就无法准确预测轴承的摩擦润滑情况。 ALLMAIER等[11-12]计入温度和轴瓦、轴颈表面粗糙度对润滑的影响，运用EHD方法，同时计入均值温度的影响，对径向轴承进行了研究并通过试验进行验证，对动载径向滑动轴承的研究提供了借鉴。本文作者则在前人研究基础上，基于全柔性机体，计入温度和粗糙表面对径向轴承润滑摩擦的影响，运用热弹性流体动力混合润滑模型即TEHD计算模型对船舶柴油机主轴承进行摩擦润滑研究。

1 基本理论和控制方程

1.1 柔性机体和曲轴耦合方程

机体和曲轴耦合方程[13]为

(1)

为减少计算量，对机体和曲轴有限元模型进行模态缩减，得到二者柔性耦合方程

(2)

式中：M、C、K为质量、阻尼和刚度矩阵，加上横线为缩减后物理量；x为物理坐标,θ为曲轴旋转角坐标；R包含曲轴和机体的外载荷、离心力和科氏力；Q包含油膜力和微峰接触力;下角标θ、f代表刚体旋转和柔性变形；上角标b、c代表机体和曲轴。

1.2 广义Reynolds方程

对于轴承润滑，基于JFO边界条件，建立包含滑油填充率的扩展Reynolds方程[14]。

(3)

其中

(4)

运用有限体积法求解Reynolds方程，边界条件参见文献[1]。

1.3 油膜厚度方程

油膜厚度方程[15]为

h=h0+δpS+δpJ-δTJ-δTS

(5)

式中：h0为不计轴瓦变形的油膜厚度；δTS、δTJ分别为轴承、轴颈表面热变形量；δpJ、δpS分别为轴颈、轴瓦压力弹性变形。

因轴颈硬度远大于轴瓦，取δpJ=0。

1.4 油膜、轴瓦和轴颈能量方程

忽略热辐射和体积力影响，滑油能量方程[16]为

(6)

式中：μ0为边界摩擦因数；k为流体导热系数;cp为滑油比热容;u、v、w为x、y、z方向的流体速度;T为油膜温度。

轴承轴瓦热传导方程满足

(7)

式中：r为径向坐标；TS、cS、ρS、kS分别为轴瓦温度、比热容、密度、热传导系数。

轴颈表面视为等温体，其热流量方程为

(8)

式中：λf为滑油热导率；TJ为轴颈温度。

所有能量方程的热边界条件参见文献[1]。

1.5 微凸峰载荷

基于Greenwood-Tripp理论[17]，轴承表面粗糙接触压力为

(9)

其中：

(10)

1.6 主轴承载荷

主轴承载荷包括油膜载荷和微峰接触载荷，则轴承反力为

(11)

式中：B为轴承宽度；pac为微凸峰接触压力；p为油膜压力。

1.7 摩擦功耗

在弹性流体动力混合润滑区域，摩擦功耗Pf由微峰摩擦功耗和流体摩擦功耗组成

Pf=(FH+FA)ωR=ωR∬A(τH+τA)dxdz

(12)

式中：FH、FA分别为流体摩擦力和微峰摩擦力；τH、τA为流体剪应力和峰元剪应力；ω为轴颈角速度；R为轴颈半径。

2 数值计算方法

因曲轴和机体缩减后动力方程系统的高度非线性，计算采用向后微分(Backward Differentiation Formulae)法。因轴瓦、轴颈接触压力和油膜压力引起的弹性变形和热弹变形的相互影响，运用时间步长可变的Newton-Raphson迭代法求解，每一时间步下，满足曲轴与机体间的动平衡和轴颈、轴瓦、油膜间的热平衡。其收敛标准：动力学结构力绝对误差小于0.001 N，温度绝对误差小于0.001 K，曲轴转角小于0.001°；油膜力、微峰接触力等相对误差均小于0.1%。

3 计算结果与分析

3.1 计算模型

大型船舶柴油机为MAN 6S50MC型，6缸，额定转速127 r/min。机体和曲轴有限元模型如图1所示。图2所示为气缸内气体压力曲线，表1给出了主轴承计算主要参数。

图1 机体和曲轴模型Fig 1 Engine body and crankshaft model

图2 气缸气体压力曲线Fig 2 Cylinder gas pressure curves

表1 主轴承计算主要参数Table 1 Main parameters of main bearings

3.2 计算结果及分析

3.2.1 不同轴承座模型的影响

表2给出了2#和7#轴承在整个周期内的各主要参数的平均值。单轴承座相较于整机体模型，最大油膜压力的平均值均明显增大(2#和7#轴承分别增加34%和24%)，整周期内的最大油膜压力峰值波动剧烈，极值也明显增大(见图3)，2#、7#轴承的极大值均超过80 MPa，接近行业限值100 MPa。单轴承座最大微峰接触压力波动更加剧烈，且整周期内的最大值单轴承座模型也是明显大于整机体模型(见图4)；对于整周期内平均最大微峰接触力，同样是单轴承座模型较整机体偏大，2#、7#轴承分别大18%、16%。因此，对于最小油膜厚度，除局部区域外，多数时间单轴承座模型要小于整机体模型(见图5)，整周期内平均值也是前者偏小。从微峰接触百分比看(见图6)，二者差异较大，没有表现出明显的规律；对于整周期内的平均接触比依然如此，2#轴承中单轴承座模型的值稍小于整机体模型，7#轴承则相反。摩擦功耗则是摩擦结果的综合指标之一，包括液动摩擦功耗和微峰接触摩擦功耗。对于液动摩擦功耗，除2#轴承的单轴承座模型在部分时间波动较大外，整体较为一致(见图7)。但是，对于微峰接触摩擦功耗，同样单轴承座模型波动较大(见图8)。单轴承座模型总摩擦功耗较整体模型增加较多，2#、7#轴承分别增加44%、22%(见表2)。由此表明：单轴承座模型计算结果明显保守；整机体模型整体协调性好，整个周期内各参数变化较为平缓，与实际运行情况较为吻合。

表2 不同轴承座模型下2#和7#轴承摩擦数据(平均)Table 2 Friction data of 2# and 7# bearings under different bearing housing models (average)

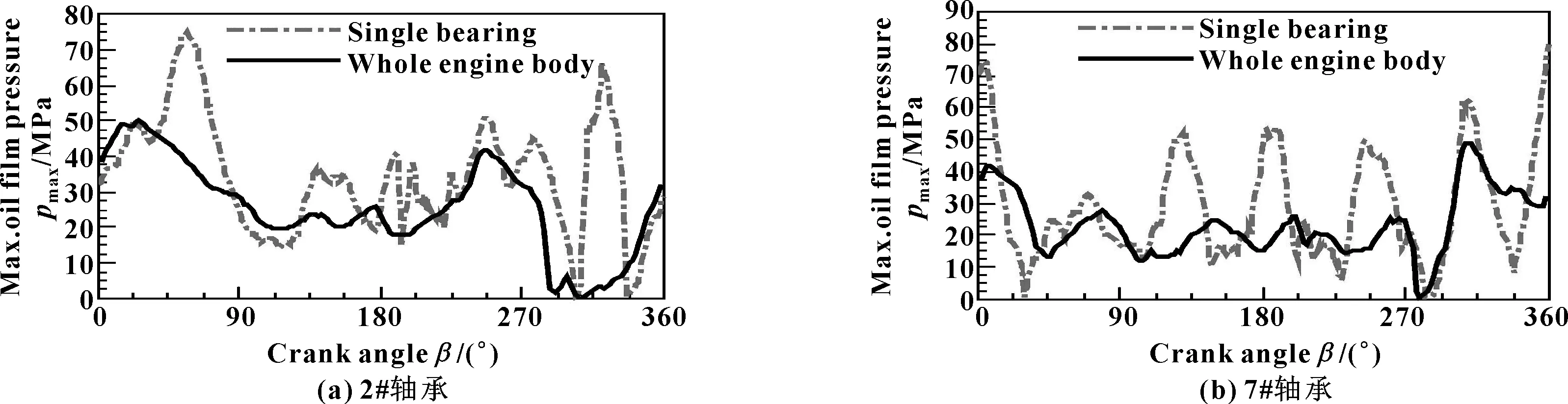
图3 不同轴承座模型下2#、7#轴承的最大油膜压力分布Fig 3 Maximum oil film pressure distribution of 2# bearing(a) and 7# bearing(b) under different bearing housing models

图4 不同轴承座模型下2#、7#轴承的最大微峰接触压力分布Fig 4 Maximum asperity pressure distribution of 2# bearing(a) and 7# bearing(b) under different bearing housing models

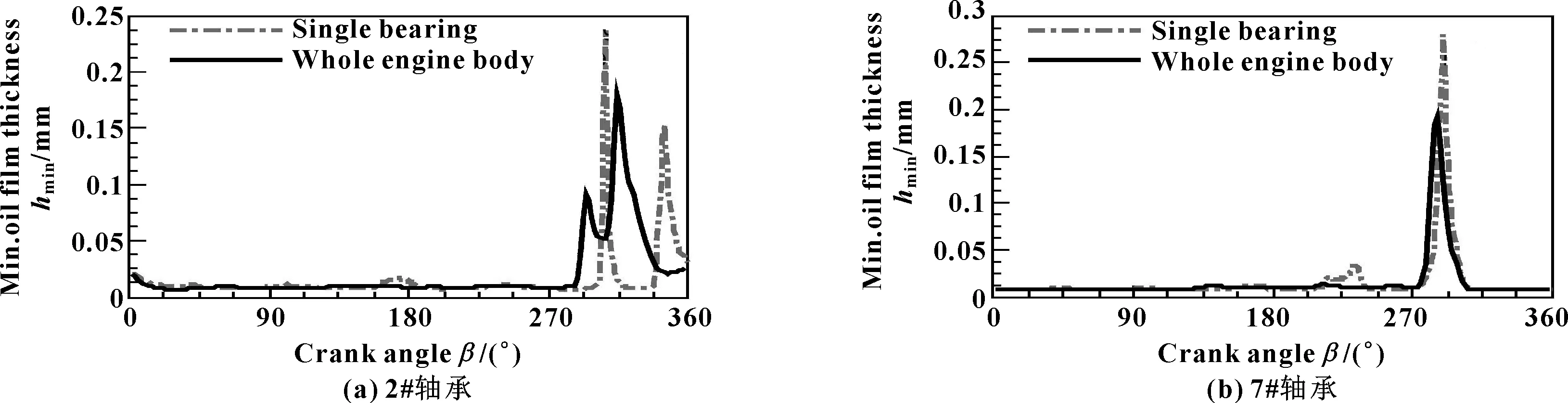
图5 不同轴承座模型下2#、7#轴承的最小油膜厚度分布Fig 5 Minimum oil film thickness distribution of 2# bearing(a) and 7# bearing(b) under different bearing housing models

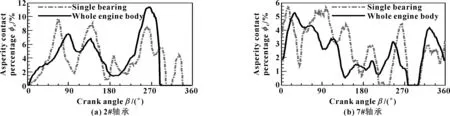
图6 不同轴承座模型下2#、7#轴承的微峰接触百分比Fig 6 Asperity contact percentage of 2# bearing(a) and 7# bearing(b) under different bearing housing models

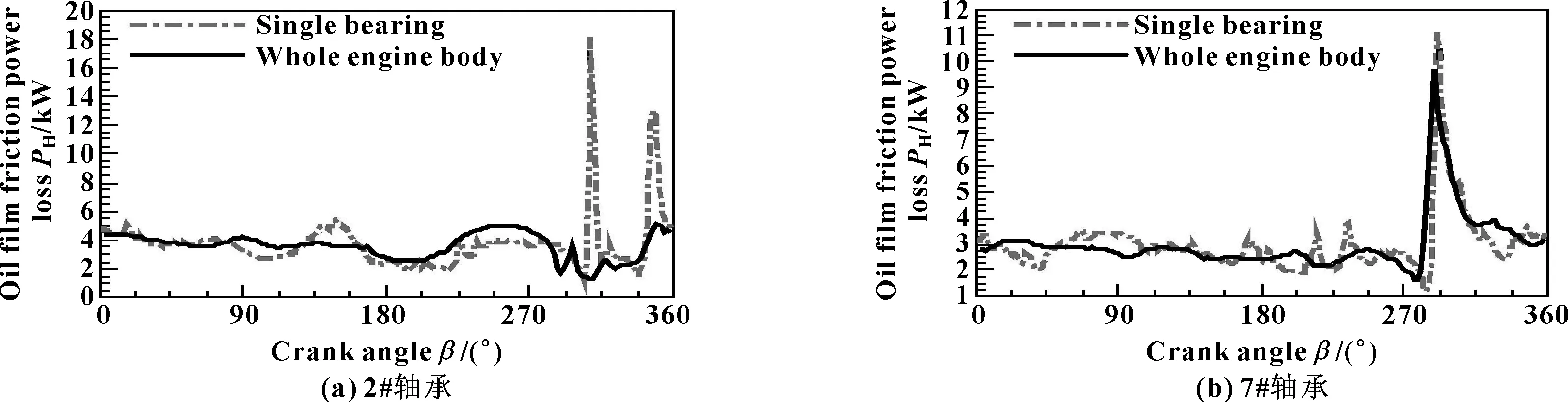
图7 不同轴承座模型下2#、7#轴承的油膜摩擦功耗Fig 7 Oil film friction power loss of 2# bearing(a) and 7# bearing(b) under different bearing housing models

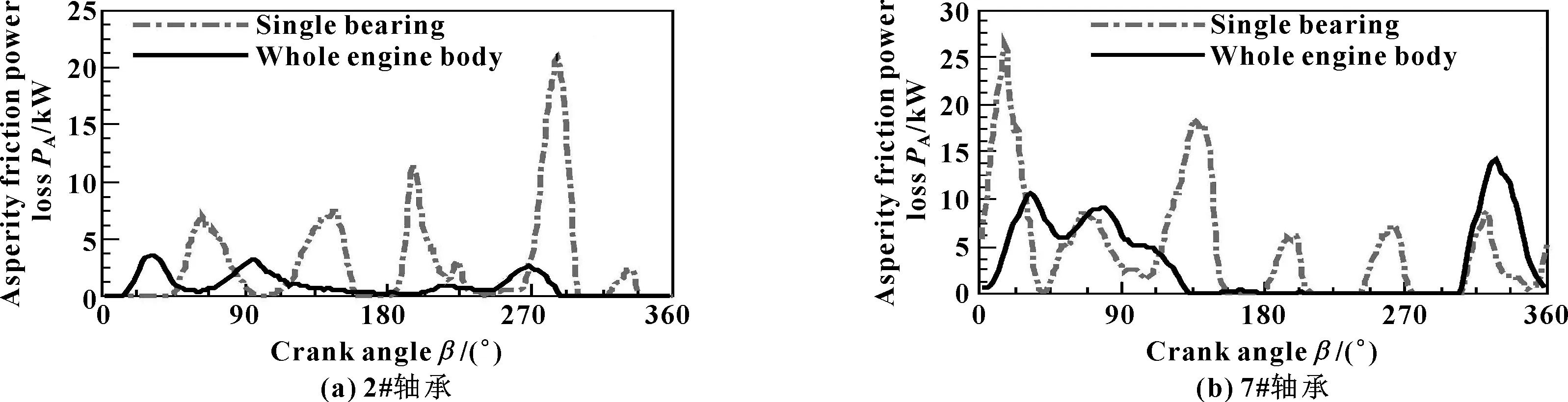
图8 不同轴承座模型下2#、7#轴承的微峰摩擦功耗Fig 8 Asperity friction power loss of 2# bearing(a) and 7# bearing(b) under different bearing housing models

3.2.2 整机体模型下主轴承热弹混合摩擦特性验证与对比

在整机体模型下，主轴承处采用不同的计算模型进行对比分析。计算结果见表3。其中THD模型，考虑动态油膜黏温特性，曲轴和机体假设为刚体，即不考虑温度和压力对机体、曲轴影响；EHD+T模型，曲轴和机体为柔性体且考虑定值温度影响，未考虑温度对油膜黏度影响，即油膜黏度为定值；TEHD模型，曲轴和机体为柔性且考虑温度对其影响，考虑温度对油膜黏度影响；ALLMAIER方法[11]，计入温度对油膜影响，温度为轴瓦表面温度、滑油入口和出口温度的均值，计入轴颈、轴瓦、油膜的能量平衡，未考虑温度对机体和曲轴的热膨胀影响，但经试验证明该方法可靠。在图9中， THD模型计算的最大油膜压力在一个周期内有6个峰值，与6个气缸的发火相对应，相对波动较小，与ALLMAIER方法差异较大。在2#轴承中，EHD+T模型和TEHD模型与ALLMAIER模型较为一致；在7#轴承中，三者虽然趋势较为一致，但在局部区域EHD+T模型波动较大，而TEHD模型和ALLMAIER模型则较为一致。对于最大微峰接触压力(见图10)，THD模型与另外三模型相比，几乎可以忽略。TEHD模型峰值变化最大，但与ALLMAIER模型最为接近，表明温度升高引起油膜黏度变小会导致局部区域的微峰接触。反映在最小油膜厚度上(见图11和表3)，TEHD、EHD+T和ALLMAIER模型三者趋势比较一致。当然，TEHD模型油膜厚度均值整体较EHD+T模型稍小，表明油膜黏度变小会降低其载荷能力，THD模型则仍较为理想，最小油膜厚度变化小、厚度大。至于微峰接触百分比(见图12)，THD模型在2%～5%间波动，EHD+T、TEHD和ALLMAIER模型则变化较大，三者并没有反映出一定的一致性，表明微峰接触较为复杂。当然从平均值看， TEHD模型明显较EHD+T模型偏大(见表2)。依据Hs≥4为全液动润滑判断，即只要h>19.42 μm，综合图11和图12判断，THD模型整周期内几乎全部为液动润滑，而EHD+T、TEHD和ALLMAIER模型则少量时间为液动润滑，其余大部分时间均有微峰接触，仅接触百分比较低而已。从图13、14可知，THD模型中液动摩擦功耗波动很小，微峰接触功耗几乎可以忽略；TEHD模型和ALLMAIER模型的液动摩擦功耗较为一致，而EHD+T模型的液动摩擦功耗较二者明显偏大，但趋势基本一致；微峰接触功耗，除THD模型外，其他三种模型同样未表现出明显一致的趋势，但波动的范围差异较小。从表3中的平均值看，1#—8#轴承的总功耗，EHD+T模型较TEHD模型至少高19%，说明计入动态温度对油膜的影响后，整体摩擦功耗降低。原因就是，黏度降低虽然微峰接触百分比增加(TEHD模型中)，但总体百分比较低(平均没有超过5%)，多数时间为液动润滑，液动摩擦功耗占整个摩擦功耗的比例较大，占主导作用。EHD+T模型中油膜黏度较大，故整体摩擦功耗也较大。通过THD、EHD+T和TEHD与ALLMAIER模型对比表明：在大型重载的整机体模型中，THD模型过于理想，忽略机体和曲轴的热弹性能将无法准确反映润滑形貌。EHD+T和TEHD模型相对能够反映整个柔性机体和曲轴模型下的摩擦特性，尤其是TEHD模型与ALLMAIER模型相对较为一致，更具可靠性。同时，EHD+T模型的摩擦功耗较高，表明温度对重载轴承摩擦特性的影响不可忽略。

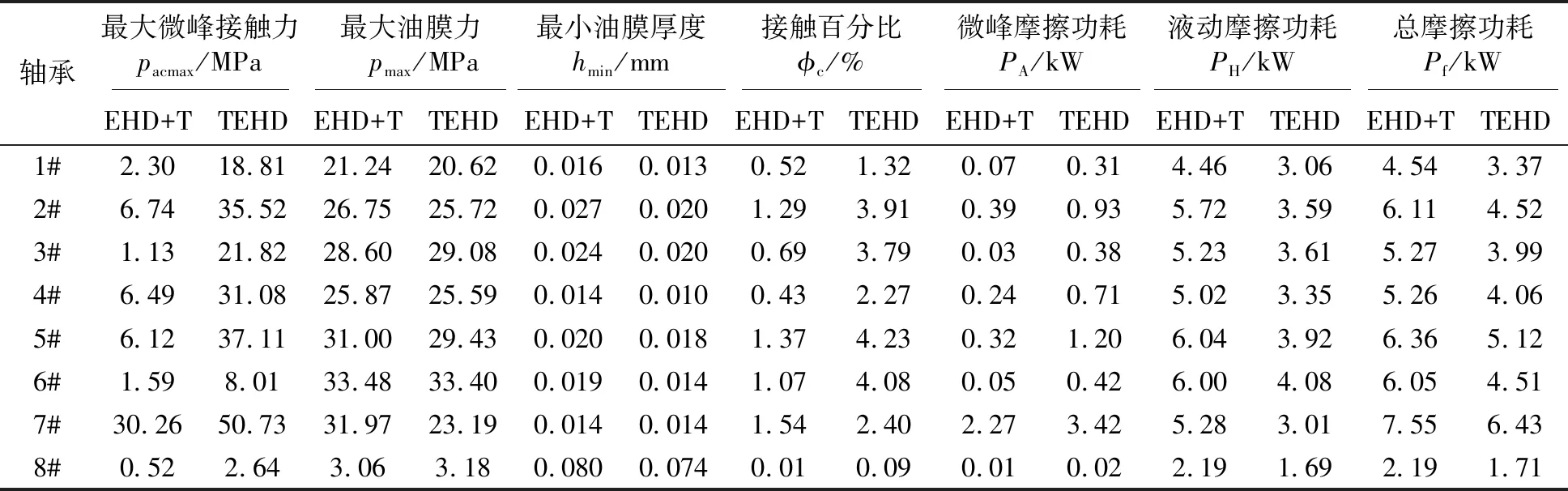
表3 不同润滑模型下各主轴承主要摩擦数据(平均值)Table 3 Friction data of all bearings under different lubricating models (average)

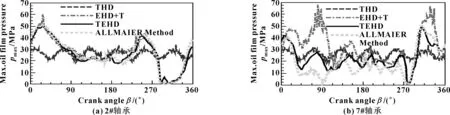
图9 整机体模型下2#、7#轴承的最大油膜压力分布Fig 9 Maximum oil film pressure distribution of 2# bearing(a) and 7# bearing(b) under whole body model

图10 整机体模型下2#、7#轴承的最大微峰接触压力分布Fig 10 Maximum asperity pressure distribution of 2# bearing(a) and 7# bearing(b) under whole body model

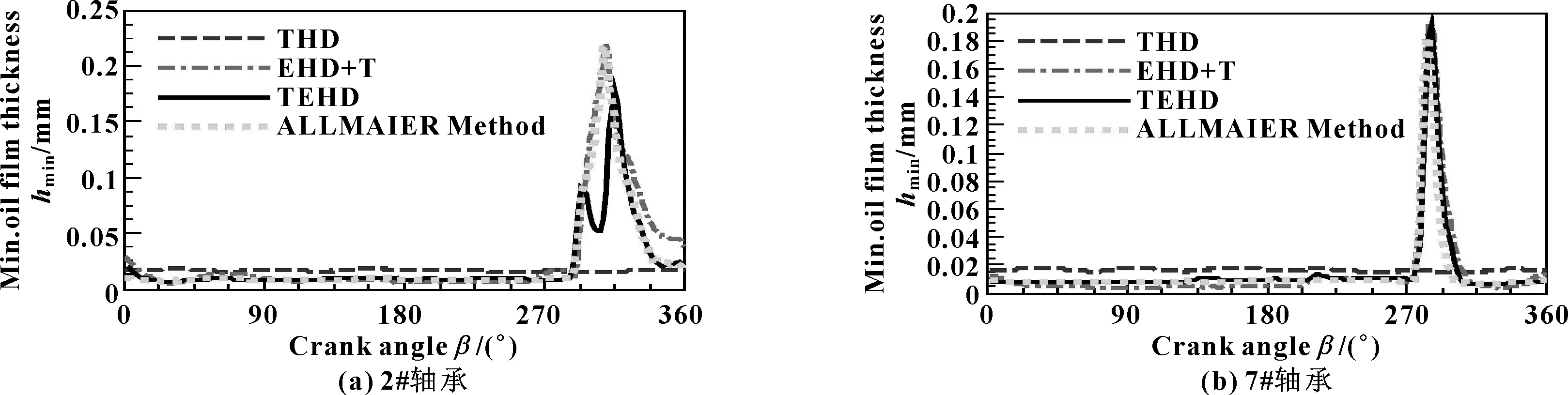
图11 整机体模型下2#、7#轴承的最小油膜厚度分布Fig 11 Minimum oil film thickness distribution of 2# bearing(a) and 7# bearing(b) under whole body model

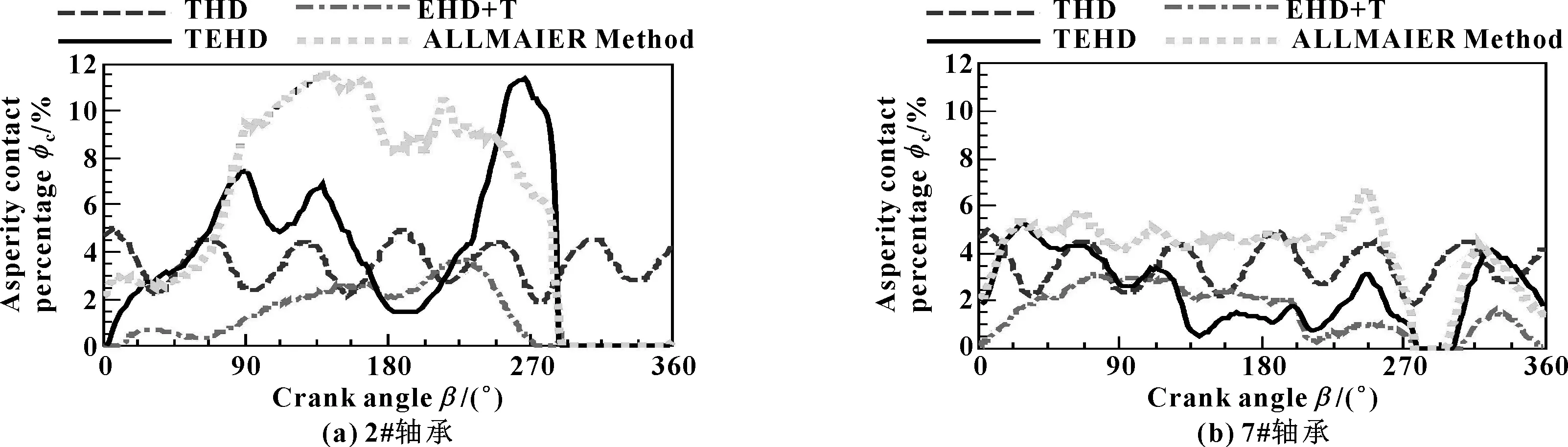
图12 整机体模型下2#、7#轴承的微峰接触百分比Fig 12 Asperity contact percentage of 2# bearing(a) and 7# bearing(b) under whole body model

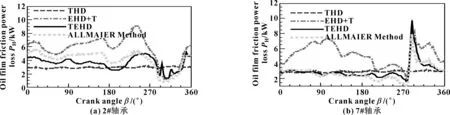
图13 整机体模型下2#、7#轴承的油膜摩擦功耗Fig 13 Oil film friction power loss of 2# bearing(a) and 7# bearing(b) under whole body model

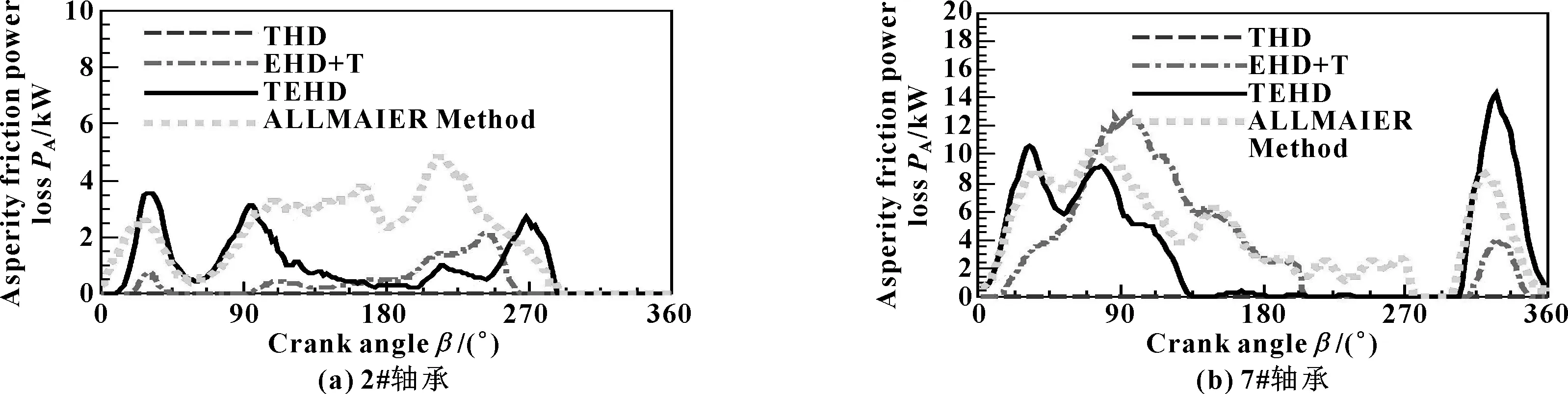
图14 整机体模型下2#、7#轴承的微峰摩擦功耗Fig 14 Asperity friction power loss of 2# bearing(a) and 7# bearing(b) under whole body model

4 结论

(1)若主轴承处均采用TEHD模型，单轴承座模型计算结果过于保守，摩擦功耗偏高，载荷波动剧烈。而整机体模型下，载荷变化平缓，说明整机体能够平衡柔化各轴承载荷。

(2)通过与ALLMAIER模型对比，在大型重载船舶柴油机中，主轴承采用THD模型计算结果将过于理想，参考价值较小；EHD+T和TEHD模型则有较高的可靠性，TEHD模型最为适宜。

(3)在整机体模型下，EHD+T模型较TEHD模型的摩擦功耗偏大，表明温度对油膜的影响将会对主轴承的摩擦特性有重要影响。因此，对轴承做精确计算时，TEHD模型较好；在非精确、非重载或工况较为稳定情况下，EHD+T模型也可以满足需求。