基于ANSYS的电力线路金具的轻量化设计

胡俊前，杨 群，戴洋洋

1.芜湖职业技术学院机械工程学院，安徽芜湖,241006；2.南京苏豪电气有限公司，江苏南京,211100

输变电元件是连接和组合电力系统的金属附件，主要用于支持、固定线缆。随着我国的电网覆盖面积不断增大，输变电元件的应用也越来越广泛，高强度、轻重量、弱磁性的线路金具可以有效提高布线的效率，增加线路的可靠性和稳定性[1]。其中，基于铝质或铝合金材料的线路金具应用最为普遍。目前国外已经大规模使用铝制金具，甚至在工程招标中明确规定使用铝制金具。国内受制于成本和设计水平的限制，目前仍处于钢制金具和铝制金具共存的局面，其主要原因在于铝制金具和铝合金金具虽然具有重量轻和弱磁性等优点，但是强度较低，使得同等载荷情况下，铝制金具的体积增大，重量增加，影响金具的携带和安装等使用的方便性[2]。这就涉及轻量化设计的问题，即通过模拟产品的实际工作状态对金具进行强度分析，进而对金具的结构进行拓扑优化以减轻重量，达到降低材料使用量，提高金具承载能力的目的[3]。在这方面，国内使用最多的是ANSYS有限元分析软件，因其强大的应力分析能力和后处理功能,广泛应用于工业产品的优化设计，但在金具设计的应用上更多是集中在金具的工况分析和强度分析方面[4-5]，却很少涉及结构优化设计。本文以高压输变电线路中广泛应用地联接金具心形环为设计对象，借助ANSYS有限元分析软件对心形环进行结构静力分析并基于此分析结果对其进行结构优化和轻量化处理，提出金具设计的新理念和新方法，提高金具的设计效率。

1 逆向建模

进行有限元分析的模型与实际使用零件要求高度接近，这样分析结果的可靠性较高，能够反映实际零件的工作状态[6]。鉴于实际的心形环金具是通过金属压铸工艺制造，实际零件与理论设计模型误差较大，所以本次设计使用Geomagic逆向软件对心形环的实体模型进行逆向设计建模。首先采用Geomagic Wrap进行点云采集和数据处理，获得与原件真实度较高的面片模型；第二步使用Geomagic DesigX逆向建模软件设计心形环的三维数字原模型；第三步使用Geomagic DesigX自带的数字模型比对功能将逆向原模型与面片模型进行比对，在确认误差合理的情况下输出到有限元分析平台进行分析。

逆向建模的结果如图1所示。图1a为心形环的逆向原模型，图1b为逆向原模型与面片模型的比对情况，可以观察到原模型上基本所有区域都被绿色所覆盖，即逆向原模型与扫描数据的体偏差大体在-0.1～0.1范围内，二者贴合度很高，所以建模是符合要求的[7]。

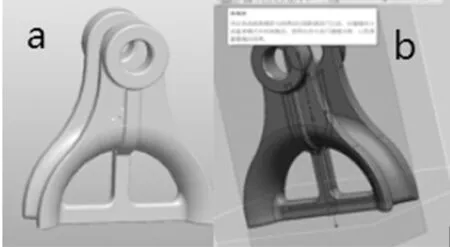
图1 完成逆向建模的心形环模型

2 有限元分析

2.1 心形环原模型系统有限元模型的建立

将逆向原模型导入Pro/E中，在Pro/E环境中与预先创建的其他零件进行组装，创建心形环工作模型，双击该软件中的ANSYS接口，就可直接打开Workbench软件并在其中显示装配后的模型，导入后的心形环工作模型如图2。

图2 心形环工作模型

定义模型。ANSYS软件的有限元分析采用的是模型结构离散化的分析方法[8]。首先将连续的实体模型表面离散成若干个单元，其中每个单元上的节点起着连接相邻单元的作用，采用位移法，分析单元的力学性质，其过程就是构造单元应力、单元应变和节点位移与节点应力之间的函数关系的过程，与此同时可以得到单元的刚度矩阵；其次，将先前获得的单元刚度矩阵合并为整体刚度矩阵，借助平衡时的载荷条件和边界条件组合原本被离散的单元，并将这两个已知条件带入结构整体的平衡关系式中，可以得到所有节点位移，再由节点位移分别带入相应的关系式中得到单元应变和单元应力。基于这个原理，ANSYS软件为模型的定义提供4种方法，即定义模型的4个步骤和定义内容：

第一步,赋予材料属性，工作模型的所有零件(包括线缆)的杨氏模量和泊松比都要定义，便于后面设置边界条件的需要，抗拉强度只定义分析的零件，其他零件无须定义，默认为无穷大，即在加载时不会出现断裂[7]，如表1所示：

表1 零件材料属性定义

第二步,定义接触类型，主要考虑连接面的接触选择对被分析零件的影响，将线缆心形环设置成有摩擦接触，选择两者接触状态为面接触，摩擦系数为0.2。

第三步,划分网格，即工作模型的离散化，建立有限元分析模型，ANSYS根据零件形状提供多种网格划分方法，因为心形环模型不是规则的几何体，选择四面体法更有利于有限元的分析和计算，划分好网格后的几何体如下图3所示，单元数70 010，节点数43 056。

图3 心形环系统的有限元模型网格划分

第四步,设置边界条件，根据实际零件的工作载荷大小以及约束情况，设置成该装配体中线缆的两个底面(A处和B处)受力均为20 kN，合力为40 kN，方向沿以心形环为基准新建的坐标系中的Z轴的力；销钉的一个外圆柱面(C处)设为固定约束；给线缆(D处)设置一个基于新建坐标系的位置约束，其中X轴和Y轴的偏离量为0。边界条件设置如图4。

图4 心形环系统的边界条件设置

2.2 心形环原模型的有限元分析结果

图5是对心形环工作模型进行静力分析后得到的总变形云图、安全系数云图，图6是心形环工作模型的应力云图，这三张几何云图与原模型的比例均为1∶1。

图5 心形环工作模型总变形和安全系数云图

图6 心形环工作模型应力云图

图5中所示的红色区域安全系数<1，根据有限元仿真分析的结果可以得出，处于工作状态下，心形环分别在总变形云图与应力云图中红色区域的变形量和应力值最大。根据安全系数的结果来看，如果心形环长时间在工作载荷的作用下，图示的红色区域可能会发现断裂情况即零件失效。

图6的应力云图中a为心形环整体的应力云图，b是a中标示为1处的放大图，1处被红色区域所覆盖，即1处是整个结构中应力最大的区域，所以需要降低1处的应力值。如果应力云图中红色区域能够连续覆盖两层及其以上的单元就可以得出划分的网格精度是足够的，即可以由图6的b推测出本次的网格划分对心形环静力分析结果准确性的影响忽略不计[9]。

3 心形环原模型的结构优化

优化零件的结构是指当模型材料、工作时的载荷、加工工艺等均不变的情况下，按某种目标(如重量最轻、成本最低、刚度最大等等)求出最好的设计方案。本文通过Pro/E对心形环工作模型进行改进，再将改进后的模型导入ANSYS中和第一次相同的参数设置去进行结构静力分析，对比优化前后心形环的分析结果判断是否能达到设计要求。

3.1 优化方案一

由心形环工作原模型的静力分析结果得知应力最大值基本集中在1处这个圆角过渡的地方，所以只需要保证1处的应力值能够低于抗拉强度就能保证心形环的强度设计要求。如图7所示，在1处增添加强肋，a为心形环原始工作模型，b是a中标示为1处的放大图，c为在心形环原模型的1处增添加强肋后的放大图。本次优化设计采用模糊尺寸策略，即优化后的模型质量的增加量以不超过原模型质量的20%为准。

图7 优化方案一

将优化后的模型保存成“X_T”格式，导入至ANSYS中，材料属性、接触定义和边界条件设置均和之前的心形环原系统各项目设置相同，经仿真后得到的总变形云图和应力云图分别如图8和图9。

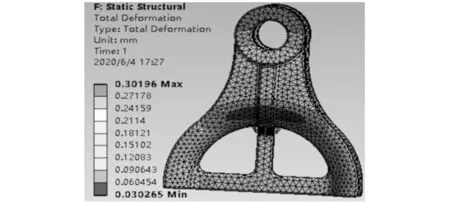
图8 用方案一改进后心形环的总变形云图

图9 用方案一改进后1处的应力云图

可见经由方案一改进之后，心形环的最大变形量和最大应力值都得到了明显的减小，但是最大应力区域的该圆角处应力值是331.02 MPa，仍然远远大于心形环的抗拉强度155 MPa，所以仍需改进。进一步扩大加强肋的尺寸，理论上是可以降低1处的应力，但重量会继续增加。

3.2 优化方案二

第二个方案是增加了原模型环形槽的截面尺寸，即下图10中a图标记为2的截面尺寸。图3-4中a为心形环原模型的剖面图，b为用方案二改进后的剖面图，即增加心形环槽底部的截面厚度。由于现代制造工艺大都采用数字三维模型进行编程和模具开发，所以本次优化设计仍采用模糊尺寸策略[10]，以质量的变化量为基准，即优化后的三维数字模型的质量较原模型质量增加20%，后期轻量化设计时再优化并减轻同样的质量，就可以实现在不增加金具重量的前提下提高承载能力的目的。

图10 优化方案二

得到的总变形云图和最大应力处1的应力云图分别如下图11和图12所示。

图11 用方案二改进后心形环的总变形云图

图12 用方案二改进后1处的应力云图

分析结果显示方案二的最大变形和最大应力与原始模型及方案一的结果对比都得到了改善。且由方案二改进后的心形环应力最大值为145.92 MPa，小于心形环的抗拉强度155 MPa，说明通过第二个方案可以避免在1处发生的断裂现象，能够达到提高心形环的结构强度的设计要求。

3.3 优化结果分析

从心形环模型的有限元分析结果来看，心形环在实际工作状态下，最大应力出现在模型的结构1处是确定无疑的，由表2的最大变形量看，从结构力学分析，由于受到力的传导性的影响，结构1处的受力集聚，应力比较集中。方案一是在结构1处增加了加强筋的设计，目的是通过增加受力面积来降低应力，没有从根本上解决应力的集聚效应，虽然有一定的效果，但要继续降低应力，就会使金具的重量增加很多。方案二改变了原模型环形槽底部的尺寸，实际上是改变了环形槽的曲率半径，降低了应力集中效应[10]，从而有效地降低了结构1处的应力，从分析结果来看，效果明显。两次优化的结果比对列于表2。

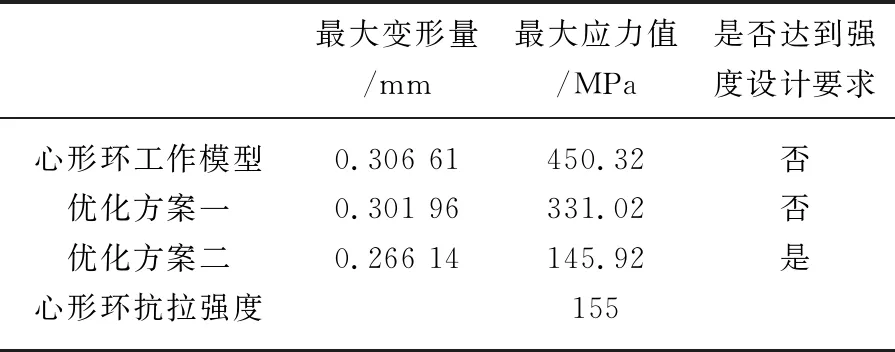
表2 用方案一、二优化后的结果总结

4 心形环结构的轻量化设计

轻量化设计归根结底是对产品结构的拓扑优化的问题，拓扑优化的方法就是保证优化设计后的零件其强度和刚度满足工作要求，然后选择其中某个和几个可变的参数进行修改，以使零件的质量达到最轻的目标[11]，是将一个连续体的结构优化问题转换成在给定材料和体积的条件下，求最小值的数学问题，其典型的函数表达式如下[12]：

Ke=(Xe)pK0

(1)

式中,Ke为单元的刚度；Xe每个单元的相对密度；K0为单元的固有刚度；p为惩罚因子，且p>1。

ANSYS中的形状拓扑优化功能采用命令流的方式进行，避免了上述复杂的数学运算，把轻量化设计过程变成简单的参数设置，其具体做法是：

第一步,选择方案二有限元分析的结果为基础作形状拓扑优化；

第二步,选择优化区域，选中装配体中的心形环作为接下来要优化的几何体；

第三步,设置边界条件，因为在第一步已经建立形状拓扑优化与静力分析结果两者之间的数据连接，所以相当于继承了之前设置的边界条件；

第四步,定义优化过程，选择20%，意为在这里使目标模型质量减少20%;

第五步,优化仿真，求解得出的结果如图13。

图13 心形环形状拓扑优化前后的模型对比

图13中a、b分别为使用ANSYS进行形状拓扑优化前后的两个模型，b较a的质量减少了20%，实现了心形环结构的轻量化设计,符合产品的预期。

5 总 结

基于有限元分析平台对线路金具心形环的优化设计，不仅增加了铝制金具的承载能力，扩大了金具的使用范围，通过轻量化的设计，还可以保持金具原有的质量和基本结构，达到预期的设计和使用效果。设计结果表明，虽然铝制金具存在强度上的不足，但是应用现代设计技术和设计手段，通过优化结构，可以在金具的承载能力、金具几何尺寸以及金具的重量之间达到很好的平衡，使得铝制金具作为钢制金具的主要替代产品，可以成为金具产品设计的发展方向，甚至完全替代。设计中有两点值得注意：

(1)考虑到制造误差的影响，有条件的情况下，采用逆向建模进行有限元分析比使用正向设计模型更能反映产品的实际工作状况。

(2)基于力的传导作用和应力集中的影响，优化设计时要先进行简单的结构力学分析，不能只对最大应力处进行优化，这样会使零件的重量增加很多，不便于后面的轻量化设计，比如本文中的两处优化设计既满足了零件的强度要求，又保持了零件的结构合理性。