考虑电动汽车充电桩无功响应的优化调度策略

王冠，刘苏贤，赵浩然，李波

（1.山东大学 电气工程学院，山东 济南 250061；2.山东大学 山东省特高压输变电技术与装备重点实验室，山东 济南 250061；3.国网山东省电力公司枣庄供电公司，山东 枣庄 277100；4.山东大学 山东大学产业集团，山东 济南 250061）

近年来，为应对日益严峻的能源短缺与环境污染问题，光伏发电以及电动汽车受到广泛关注[1-2].间歇性光伏发电的广泛应用导致电网等效负荷峰谷差变大，光伏电源渗透率过高产生的反向功率流导致电网电压越限[3]，增加了配电系统的运行压力；电动汽车的大规模入网增加了系统的负荷，导致系统电压下降，网络损耗增加[4-5]，也给电网的安全稳定运行带来了巨大的挑战.但如果能将电动汽车作为配电网的可控资源进行合理调度，不仅可以抑制无序充电对配网造成的负面影响，还能够抑制光伏出力波动，丰富系统的控制手段[6-7].

目前，学者就电动汽车充放电调度策略开展了大量的研究，大多数集中在控制有功功率上.文献[8-10]从电动汽车的角度分析，根据各时段的预测充电量，通过实行实时电价的方式引导用户错峰充电，降低用户充电成本.文献[11-15]从微电网的角度分析，通过优化电动汽车各时段有功功率的方式来削峰填谷和降低系统的网损.新的研究证明通过逆变器控制可以实现电动汽车与电网之间的有功及无功交互[16-19].已有学者就电动汽车到配电网（Vehicleto-grid，V2G）的无功功率进行了研究，通过优化各时段电动汽车的有功及无功或是建立电压无功优化模型来达到降低网络损耗的目的[20-21].但是，文献[20-21] 未充分考虑电动汽车的充电需求和不确定性，忽视了用户特性.文献[22]综合考虑实际因素，建立了电压无功优化模型，用于充电协调和V2G 无功调度.文献[23-24]采用求解速度快的线性规划和非线性规划方法求解模型，以应对快速变化的充电场景.文献[25]采用锥优化的方法进行求解，求解速度快、效果好.然而，已有的有关V2G 无功方面的研究仅考虑了电动汽车在无功优化方面的作用，却没有把电动汽车作为储能方面的作用（削峰填谷、促进可再生能源消纳等）与之结合起来.

本文考虑了电动汽车充电桩的无功响应能力，充分发挥V2G 有功及无功的作用，对多个充电站的有功无功充放进行优化调度.首先以负荷峰谷差率最低为目标，利用二次规划方法求取各时段电动汽车的最优充放电功率；在此基础上，以系统网损最低为目标，利用二阶锥规划对本时段各充电站的有功及无功进行优化，并采用滚动优化的方法，加入反馈校正环节，以应对光伏出力及电动汽车充放电的不确定性.

1 充电桩无功响应原理

V2G 充电桩一般由AC-DC 电路和DC-DC 电路两部分组成.充电桩的无功响应能力来源于双向AC-DC 变流器[26].

三相桥式AC-DC 整流/逆变电路如图1 所示，通过对V1～V6进行正弦脉宽调制（Sinusoidal Pulse Width Modulation，SPWM），可以控制其基波分量的幅值和相位.

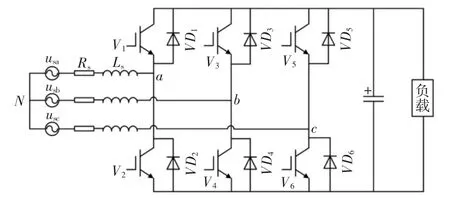
图1 三相AC-DC 变流器拓扑结构图Fig.1 Three-phase AC-DC converter topology diagram

在稳态运行条件下，以A 相为例

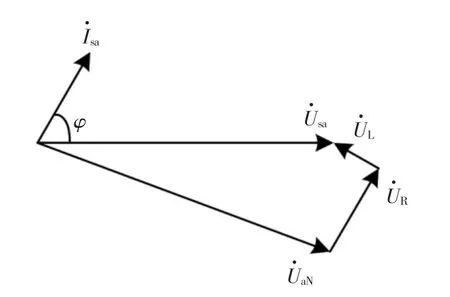
图2 AC-DC 变流器稳态运行时的基波向量图Fig.2 Fundamental vector diagram of AC-DC converter that operating in steady state

运行过程中，双向变流器传输的有功及无功受最大视在容量的限制

式中：P、Q 分别为变流器中通过的有功、无功功率；Smax为变流器的最大视在容量.

2 优化调度架构

充电桩的无功调节能力受变流器最大视在容量Smax和充放电时有功功率大小的影响.如图3 中运行点1 所示，对电动汽车进行充电，充电功率为P1，此时，充电桩可以响应的无功功率范围如图中Qav所示.

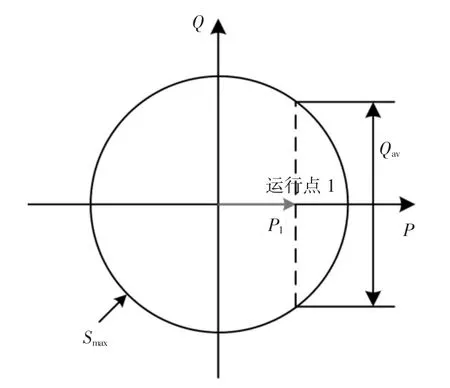
图3 充电桩中有功与无功功率运行区域Fig.3 Active and reactive power operating area in the charging pile

电动汽车数量庞大，如果对每一辆电动汽车单独制定调度计划难度较大.通过在充电站实行合理的分时电价制度，吸引电动汽车用户在峰、谷电价时段到充电站进行放、充电，可以实现对电动汽车的分群调度.

采用日前申请机制并借助智能电网相关技术的支持，实现电动汽车用户、充电站、调度中心之间的信息交互.电动汽车优化调度的具体步骤如下：

1）调度中心根据次日负荷预测以及可再生能源发电站申请出力计划制定合理的分时电价并向用户发布；

2）用户根据次日电动汽车使用情况向任意充电站申请充放电，申请信息包括：可参与充放电的时间段、申请充放电量；

3）各充电站按照峰谷电价区间的划分，将申请充放电时间段处于同一电价区间的电动汽车归为一类，并将整理后的信息上传到调度中心；

4）调度中心根据所获取的信息，采取一定的调度策略制定各充电站的有功无功充放计划，并向各充电站下发指令；

5）各充电站按照调度中心的指令对电动汽车进行充放电，并将实际充放电情况反馈给调度中心.

对上述调度策略做以下几点说明：

1）本文仅针对提交申请的电动汽车进行调度，理论上仅包括在谷电价区间申请充电以及在峰电价区间申请放电的电动汽车.将其他未提交申请随机充电的电动汽车充电负荷计入传统负荷.

2）本文按照步骤3 中所提原则对电动汽车进行归类，步骤4 中采用的调度策略仅能给出多辆电动汽车总的充放电安排.每一辆电动汽车的充放电安排在步骤5 中由各充电站根据各位用户的申请信息来完成.

3）步骤5 中各充电站根据每一辆电动汽车具体的申请信息进行充放电安排，该过程需要处理大规模数据，本文不做具体研究，仅给出该过程需要遵循的两个原则：一、各充电站在接收到调度中心下发的充放电计划后，需按照一定的优先级顺序对各电动汽车进行充放电.按照申请时段将各充电站内的电动汽车划分为两类：①当前时段是其申请时段的最后一个时段；②当前时段不是其申请时段的最后一个时段.优先级首先按照①>②排列，然后各类中每辆电动汽车的优先级按照申请时段的长短进行排列，申请时段越长，优先级越高；二、若当前时段是某电动汽车申请时段的最后一个时段，即使调度中心下发的充放电计划已经达成，仍对该电动汽车进行充放电，完成其申请要求.

3 优化调度策略

3.1 双层模型

3.1.1 实时调度层

在当前时段起始时刻，结合超短期预测数据对日等效负荷曲线进行校正，基于校正后的等效负荷曲线，以降低等效负荷峰谷差为目标，对未来各时段电动汽车的充放电功率进行优化.以每小时为单位将一天分成24 个时段，实时调度层优化目标表示如下.

目标函数：峰谷差最小

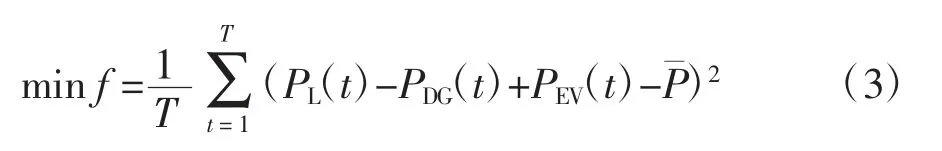
式中：T 为总时段数；PL（t）为第t 个时段基础负荷所消耗的平均功率；PDG为分布式电源出力；PEV为电动汽车充放电功率，充电为正、放电为负；P 为等效负荷平均值，通过公式（4）计算：

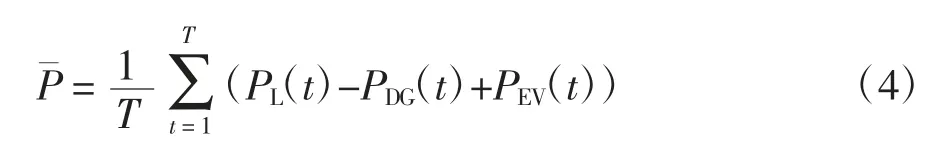
目标函数需要满足以下约束条件：

1）系统功率平衡约束

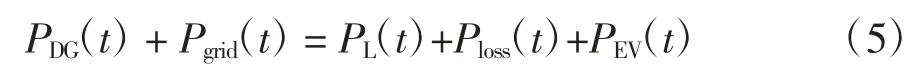
式中：Pgrid为联络线传输功率；Ploss为系统有功网络损耗.

2）电动汽车电池容量约束，包括当前时段电池容量约束以及各电价区间内的电池容量约束

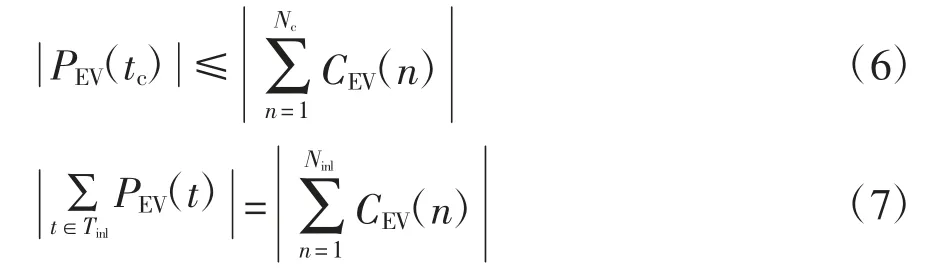
式中：PEV（tc）分别为当前时段电动汽车的调度功率；Nc为当前预约信息中申请时段包含当前时段的电动汽车数量；Tinl为某电价区间所包含的所有时段的集合；Ninl为申请时段在该电价区间内的电动汽车数量；CEV（n）为第n 辆电动汽车的申请充放电量.

3）电动汽车充放电功率约束

4）分布式电源出力约束

5）配电变压器传输功率容量限制

该模型中，目标函数为二次函数，约束条件均为线性，可以将该模型转化为凸二次规划问题进行求解：

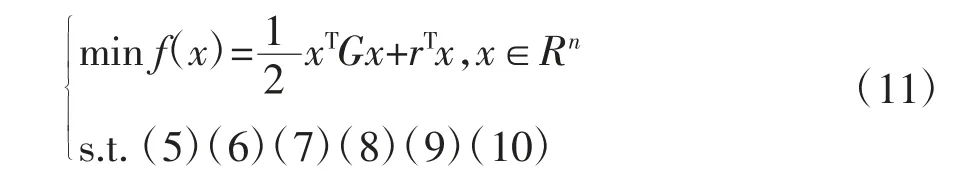
式中：x 为待优化的各时段电动汽车的充放电功率，G 等于2 倍的单位矩阵，r 是一个常数矩阵，可以通过PL、PDG得出.

3.1.2 功率分配层

根据实时调度层的优化结果可以获取本时段全系统电动汽车的最优充放电功率，以此为约束，在功率分配层对本时段各充电站有功与无功的输入输出进行优化.功率分配层的优化目标表示如下.

目标函数：系统网损最低

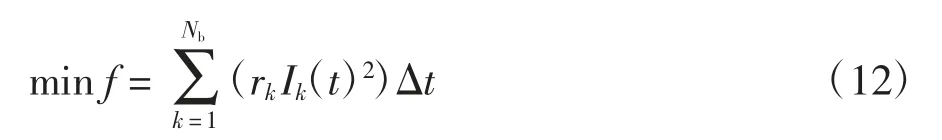
式中：rk为支路k 的电阻；Ik（t）为t 时段支路k 流过的电流；Δt 为时段长度；Nb为系统支路数目.

目标函数需要满足以下约束条件：

1）实时调度层计划功率约束

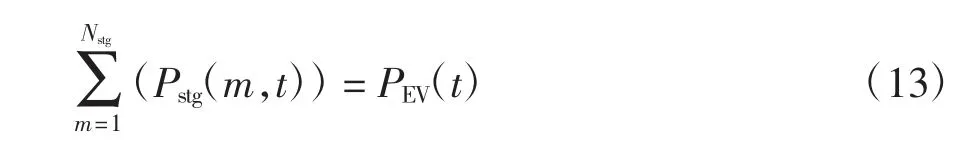
式中：Pstg（m，t）为第t 个时间段充电站m 的有功功率，充电为正、放电为负；Nstg为充电站数量.

2）电池容量约束

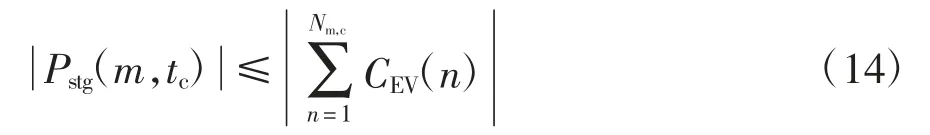
式中：Pstg（m，tc）为充电站m 在当前时段tc电动汽车的调度功率；Nm，c为当前充电站m 的预约信息中申请时段包含当前时段的电动汽车数量；CEV（n）为第n辆电动汽车的申请充放电量.

3）电动汽车充放电功率约束

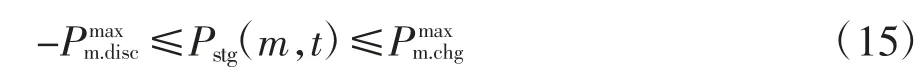
4）双向变流器的通流能力限制即最大视在容量限制

式中：Pstg、Qstg分别为充电站有的功、无功功率；Sstg.max为变流器的最大视在容量.

5）系统安全约束

6）系统潮流约束

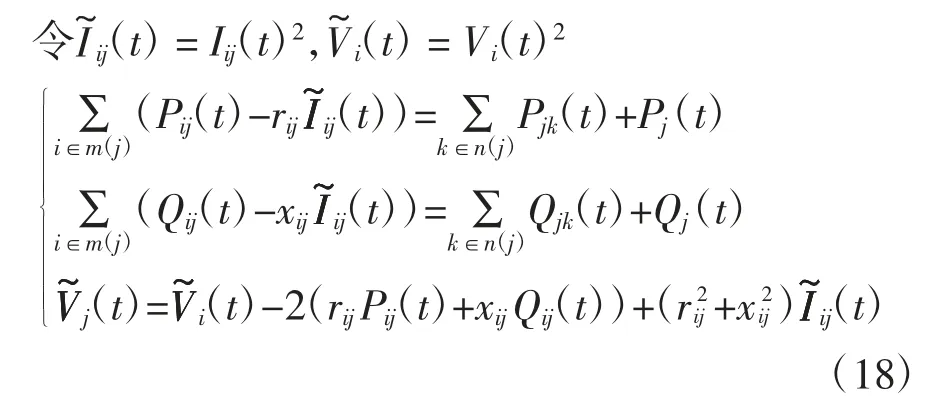
式中：m（j）和n（j）分别是以节点j 为末节点的支路的首端节点集合和以节点j 为首节点的支路的末端节点集合；Pij、Pjk、Qij、Qjk为线路上传输的有功无功功率；Pj、Qj为节点j 的净有功无功负荷；rij、xij为线路的电阻、电抗；Iij为线路上传输的电流；Vi、Vj为节点i、j的电压.

将式（18）进行松弛得到

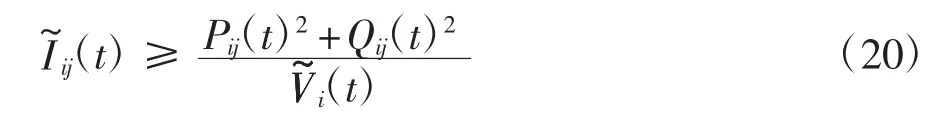
再做一步等价变形转化为标准二阶锥形式

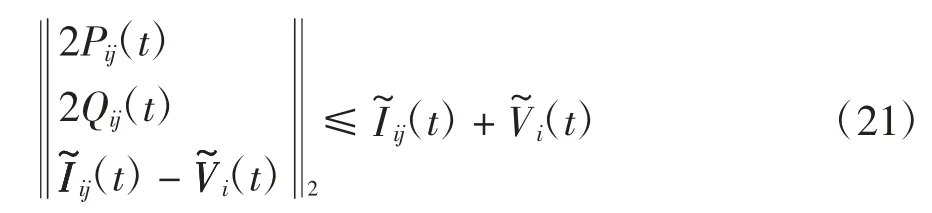
通过二阶锥松弛技术，该模型可以表示为

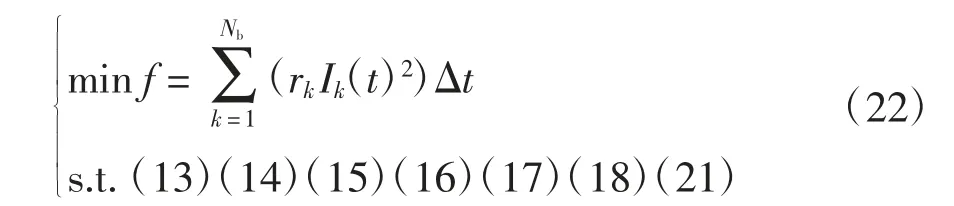
该模型中，目标函数为凸函数，约束条件（21）的数学形式满足二阶锥的定义，其他约束条件均为线性，该问题是一个二阶锥问题，同时符合凸规划的判定条件[27]，可以通过二阶锥规划求解该模型.

3.2 滚动优化

一方面，可再生能源出力以及负荷的预测值与实际值存在偏差；另一方面，该策略中对电动汽车进行分群调度，未考虑每一辆电动汽车具体的申请信息，电动汽车实际充放电情况可能偏离调度计划，此外，车主的充放电行为具有主观性，申请信息可能临时出现变动.因此，本文采用滚动优化调度的方法，加入反馈校正环节，具体流程如图4 所示.

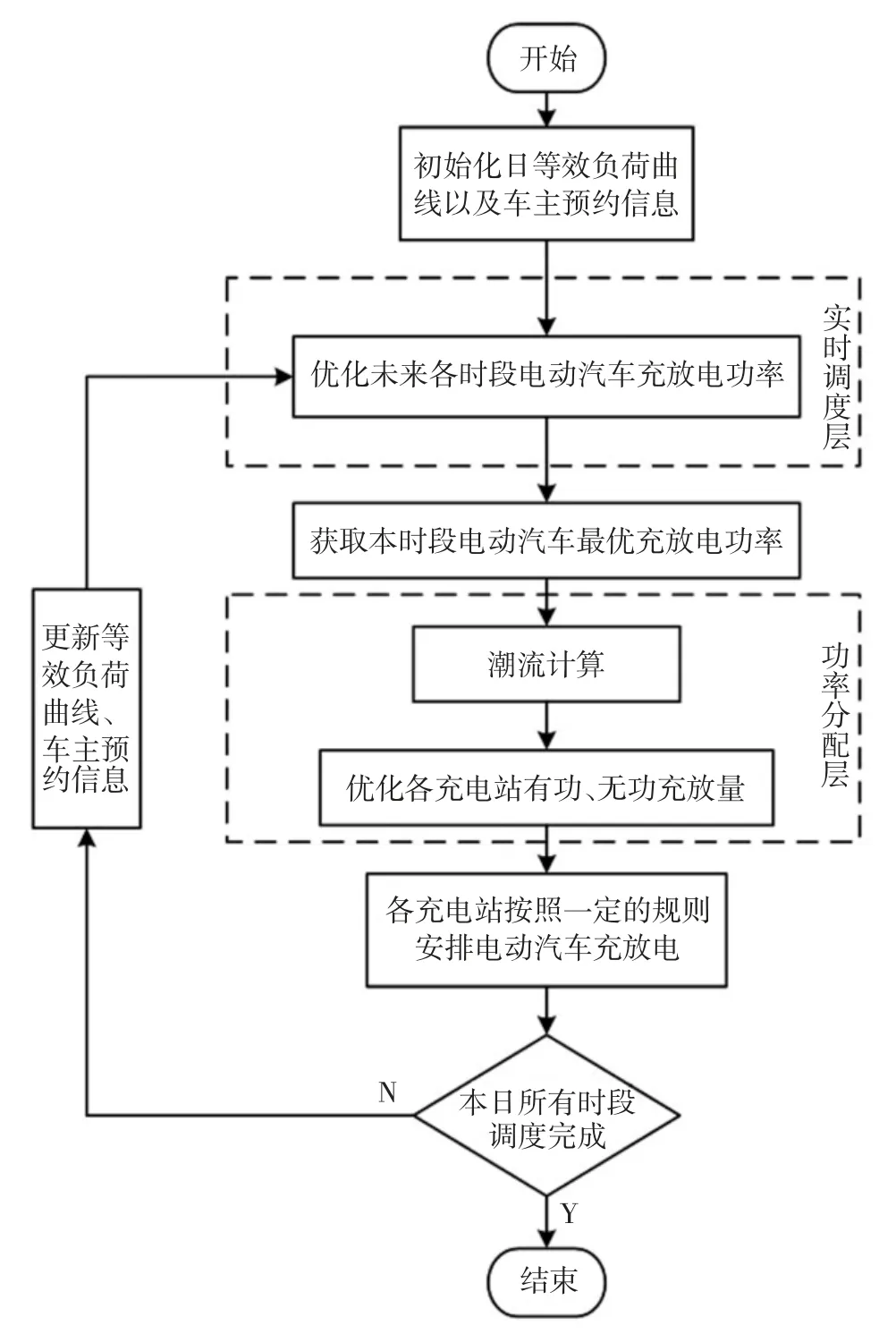
图4 滚动优化的基本流程Fig.4 Basic flow of rolling optimization

1）当前时段，结合本日可再生能源出力及负荷需求之前时段、超短期预测及日前预测数据，以及所有车主的预约信息，在实时调度层对本日未来各时段电动汽车的充放电功率进行优化，从而获取全系统当前时段的最优充放电功率.

2）在功率分配层，结合当前各充电站车主预约信息，以实时调度层的优化结果为约束，合理分配各充电站电动汽车充放电功率，同时结合双向变换器的容量限制，对各充电站的无功大小及方向进行优化.

3）下一时段，更新之前时段、超短期预测、日前预测数据；更新各充电站车主预约信息.重复上述步骤，直到本日所有时段调度完成.

4 仿真实例

本文利用MATLAB 进行编程，选取IEEE33 节点配电系统进行测试仿真，并对该系统进行改进，系统拓扑如图5 所示.光伏电站安装在节点5、18、31，装机容量分别为2.5、2、2.5 MVA，采用恒功率因数控制并网，功率因数为0.95.充电站建立在节点15、23、26，各充电站选用集中式变流器并网，双向变流器最大视在容量为0.6 MVA，充放电效率均为95%.系统基准电压为12.66 kV，基准容量为10 MVA，根节点电压为pu，可以通过改变变压器变比进行调节，其余节点电压允许变化范围为[0.95～1.05]pu，支路最大允许电流为500 A.

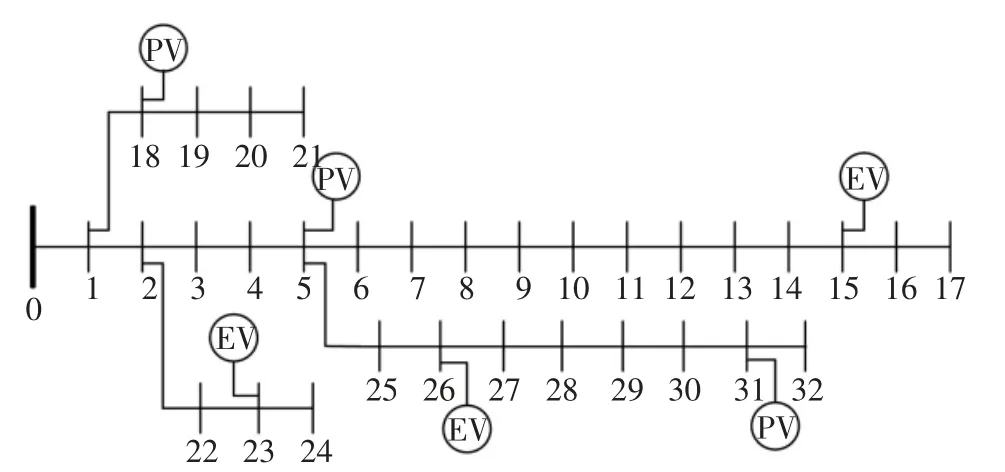
图5 改进后的IEEE 33-bus 配电系统结构拓扑图Fig.5 Improved IEEE 33-bus power distribution system structure topology

某日日前负荷预测数据以及光伏申请出力计划如图6 所示[28].

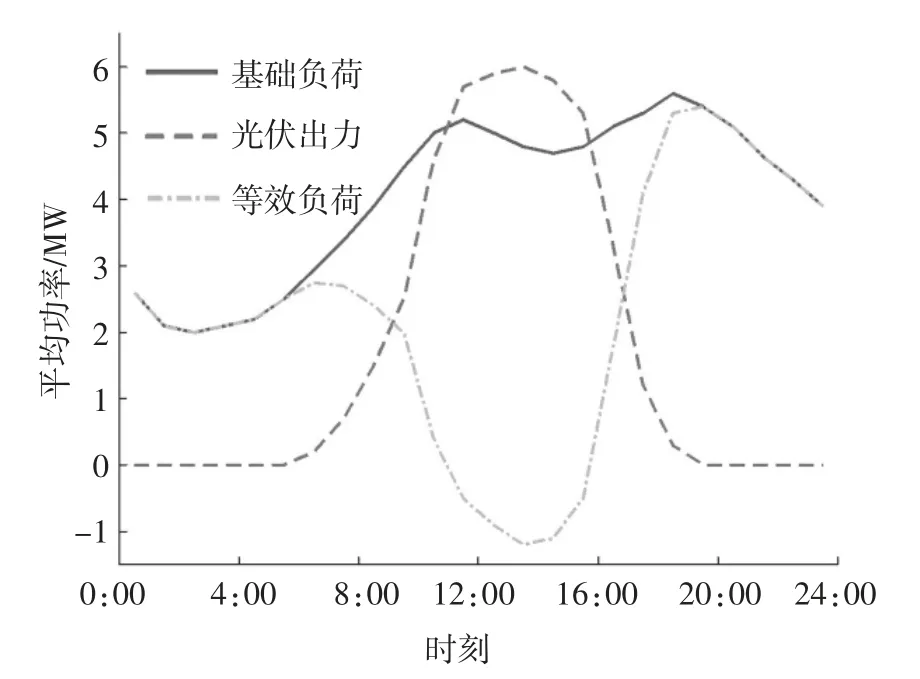
图6 光伏、负荷功率预测曲线Fig.6 Photovoltaic and load power prediction curve

据此设定10：00-17：00 为负荷谷区间，17：00-24：00 为负荷峰区间，制定峰谷电价并向用户发布.假设车主预约信息汇总后的各时段容量约束及各区间容量约束如表1、表2 所示.

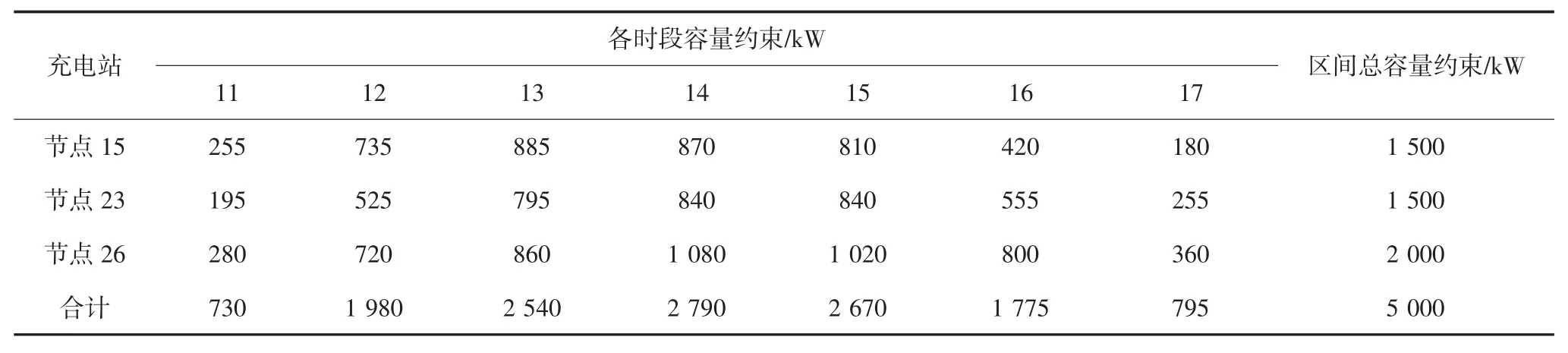
表1 负荷谷区间（10：00-17：00）申请容量约束Tab.1 Application capacity constraint of load valley（10：00-17：00）

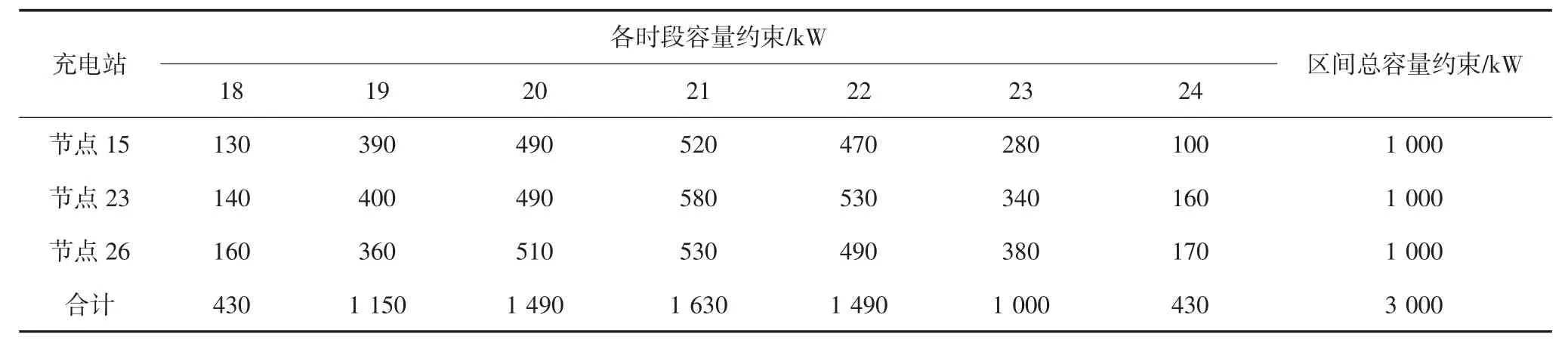
表2 负荷峰区间（17：00-24：00）申请容量约束Tab.2 Application capacity constraint of peak load（17：00-24：00）

4.1 负荷谷时段

在10：00，开始第一轮的调度，实时调度层的优化调度结果如图7 所示，得到10：00-11：00 电动汽车的最优充电功率为0，功率分配层所求得的各充电站的最优充电功率自然也均为0.对比图中两条曲线也可以看出，通过合理控制电动汽车的充放电功率能够达到“削峰填谷”的效果，明显改善了系统负荷的峰谷差.

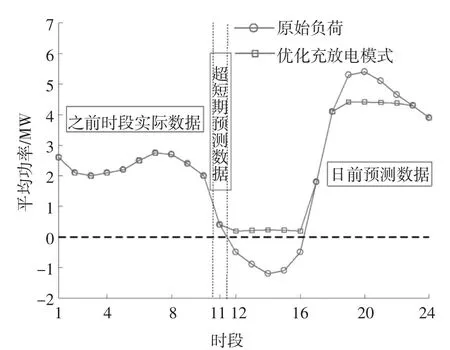
图7 第11 个时段等效负荷曲线及优化充放电结果Fig.7 Equivalent load curve and optimized results for the 11th period

倘若存在申请时段为10：00-11：00 的用户，为了满足其充电要求，10：00-11：00 各充电站实际充电功率分别为50、80、70 kW，进入下一时段后，对本时段负荷的实际数据进行校正，如图8 中第11 个时段（10：00-11：00）所示.在第12 个时段（11：00-12：00），原始负荷等于基础负荷减去光伏出力，光伏出力的超短期预测平均功率比日前预测增加了100 kW，因此原始负荷减少100 kW.对该时段的负荷曲线校正后重新优化的结果如图8 中带有方框的实线所示，优化充电功率为原始负荷加上充电负荷，由此得到本时段最优充电功率为700 kW.

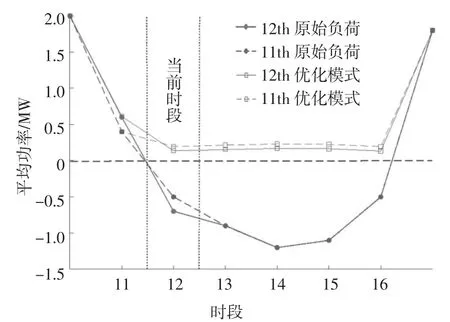
图8 第12 个时段的等效负荷曲线及优化充放电结果Fig.8 Equivalent load curve and optimized results for the 12th period

为了研究电动汽车充放电调度对电网的影响，选取以下3 个方案进行比较：

1）初始情况，即无电动汽车接入配网；

2）以网损最小为目标，仅对充电站的有功充放进行优化；

3）以网损最小为目标，考虑充电桩的无功响应能力，对充电站的有功无功充放进行优化.

分别按照方案1～3 进行求解，EV 调度方案和相应的评价函数值如表3 所示.表中节点电压偏移量由式（23）计算

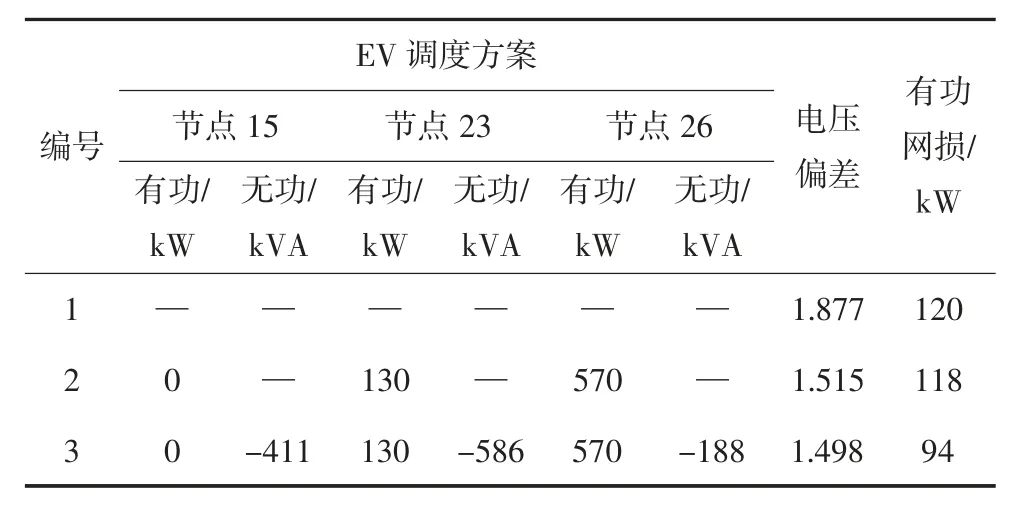
表3 第12 个时段充电站各调度方案及优化结果Tab.3 Scheduling scheme for charging station and optimization result in the 12th period

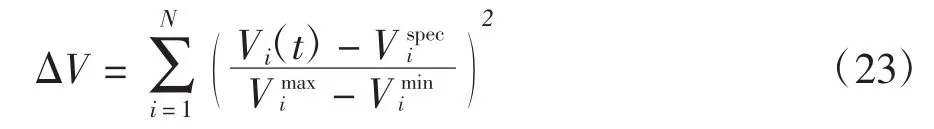
与方案1 相比，方案2 中充电站的有功优化可以显著改善系统节点电压水平，但在降低系统网损方面取得的效果不明显；方案3 考虑充电桩的无功响应对充电站进行有功无功优化可以显著降低系统网损，并进一步减小了系统节点电压偏差.图9 显示了按照方案1～3 对EV 进行调度后，IEEE33 节点配电系统各节点电压幅值变化情况.从该图可以看出，初始情况下，由于光伏渗透率过高出现功率倒送，引起光伏电站附近节点电压过高，若光伏出力进一步增加，很容易造成节点电压越限[28]；在方案2 中，通过对电动汽车进行充电吸收部分光伏的过剩出力，能够有效降低各节点电压幅值.通过对比，可以发现方案3 在调节节点电压偏移方面具有更好的优化效果.

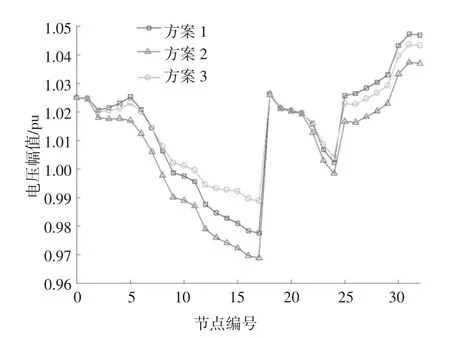
图9 第12 个时段IEEE 33-bus 配电系统各节点电压幅值Fig.9 Voltage amplitude of each node in IEEE 33-bus power distribution system in the 12th period

4.2 负荷峰时段

假设第19 个时段（18：00-19：00），实时调度层的优化结果与图7 相同.电动汽车最优放电功率为937.5 kW.

分别按照前述方案1～3 进行求解，EV 调度方案和相应的评价函数值如表4 所示.对比表3 表4 数据，可以发现在负荷峰时段，系统有功网损及节点电压偏移都要比谷时段更加严重.与初始情况相比，电动汽车有序放电可以减小节点电压偏差和网络有功损耗，若考虑电动汽车充电桩的无功响应能力，则可以进一步降低节点电压偏差及系统网损.图10 显示了按照方案1～3 对EV 进行调度后，IEEE 33 节点配电系统各节点电压幅值的变化情况.由图可知，初始情况下，由于负荷过重，多个节点出现了不同程度的越限，电动汽车储能的接入可以有效提高电压质量较差节点处电压的幅值.对比方案2 与方案3 可以看出，当考虑充电桩的无功响应时，通过无功优化即可以降低系统有功网损，也能够有效减少电压幅值变化范围，从而使得系统各节点电压幅值更接近根节点电压，系统电压分布更加均匀.

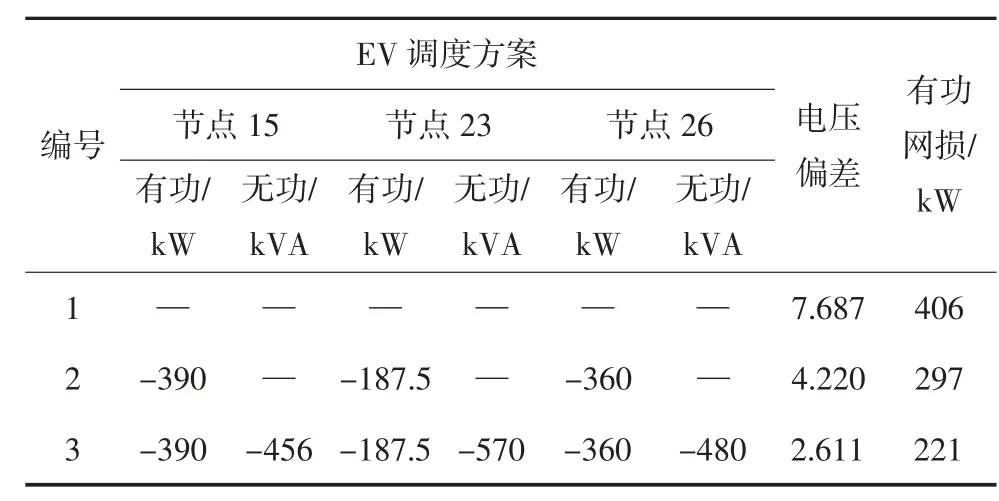
表4 第19 个时段充电站调度方案及优化结果Tab.4 Scheduling scheme for charging station and optimization result in the 19th period

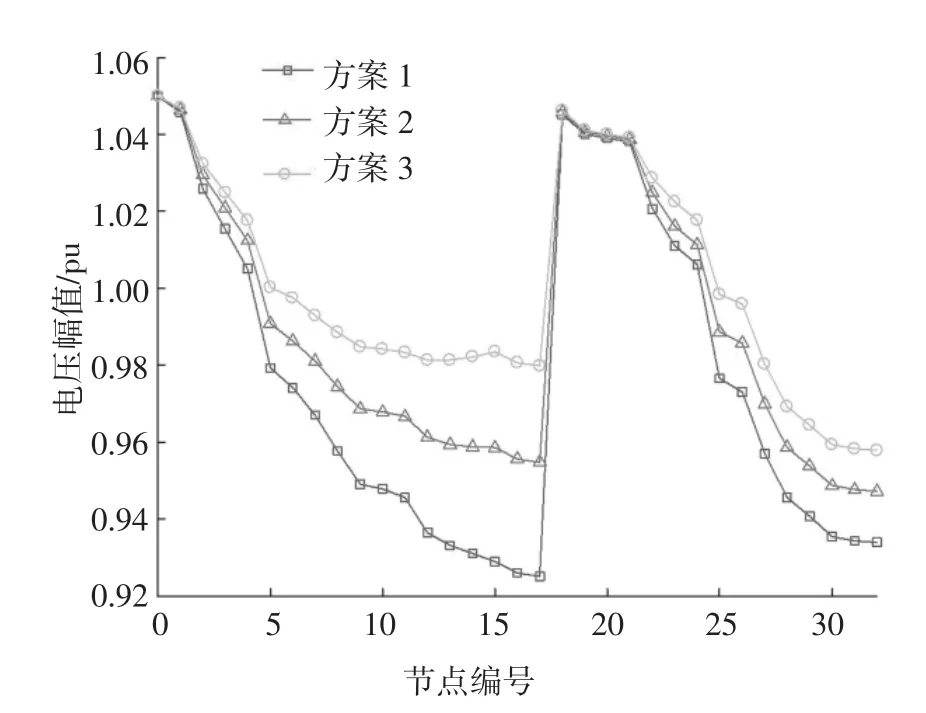
图10 第19 个时段IEEE 33-bus 配电系统各节点电压幅值Fig.10 Voltage amplitude of each node in IEEE 33-bus power distribution system in the 19th period

5 结论

本文考虑了电动汽车充电桩的无功响应能力，提出了电动汽车充电站的有功及无功调度策略；充分考虑了电动汽车的充放电需求及不确定性，采用了实时滚动优化调度方法，同时考虑了电动汽车充放电的时空分布特性，建立了双层优化模型，并分别采用二次规划、二阶锥规划求解模型.仿真结果表明，本文所采用的算法可以快速获得全局最优解，所提调度策略可以有效降低负荷峰谷差，降低系统网损，减小节点电压偏差等.