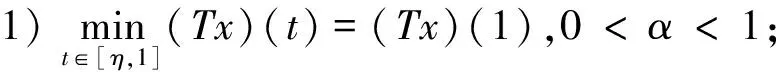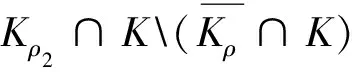带有变系数的二阶脉冲微分方程的正解

李海艳

(成都锦城学院 通识教育学院，四川 成都 611731)

0 引言

脉冲微分方程是数学领域的一个重要分支.有关非线性脉冲微分方程边值问题解的问题，很多学者对其进行了研究[1]，这些文献中涉及的方法很多，包括上下解方法、单调迭代技术、锥上的不动点定理、Leray-Schaudar原理等．此外，二阶脉冲微分方程的边值问题已经被广为研究[2]，但在这些文章中，作者总是假设非线性项f与一阶导数x′(t)无关，或者非线性方程中不含h(t)．

笔者讨论了如下边值问题(BVP)：

(1)

笔者讨论了一类二阶脉冲微分方程的三点边值问题，利用不动点指数理论获得该问题正解的存在性定理，建立了一些该问题存在正解的充分条件．

1 预备知识

为了方便，笔者列出一些定义、注解和已知的结论．

令J0=[t0,t1],Jk=(tk,tk+1],k=1,2,…,m,t0=0,tm+1=1.PC[J,R]={xJ→R|x(t)，当t≠tk时连续,存在,且当t≠tk时连续,存在，且引入范数

显然，PC[J,R]在‖·‖PC下构成一个Banach空间，PC1[J,R]在‖·‖下构成一个banach空间．

记PW[J,R]={x∈PC[J,R]|x′(t)在每个区间Jk的任意子集上绝对连续，k=1,2,…,m}.

定义1x称为BVP(1)的一个正解，若x∈PW[J,R],x(t)>0,t∈J，且满足(1)．

引理1[3]H⊂PC1[J,R]是相对紧集的充分必要条件为H中的诸函数x(t)及其导函数x′(t)都在J上一致有界且在每个Jk(k=1,2,…,m)上等度连续.

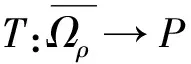
1) 如果‖x‖≤‖Tx‖，对x∈∂Ωρ，那么i(T,Ωρ,P)=0；

2) 如果‖x‖≥‖Tx‖，对x∈∂Ωρ，那么i(T,Ωρ,P)=1．

引理3 设x∈PW[J,R]满足:

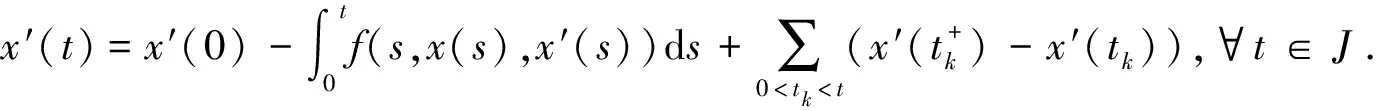
则

引理4 设x∈PW[J,R]是BVP(1)的解，当且仅当x∈PC1[J,R]是下面脉冲积分方程的解．

其中

经计算可得：

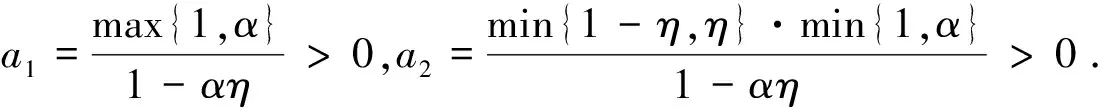
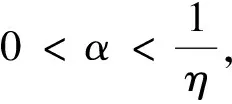
由于xJ→R+,x″(t)=-h(t)f(t,x(t),x′(t))≤0 ，可知x(t)在[0,1]上是凹的．令K={x∈P|x是凹的且其中γ如上所给．显然P是E上的一个锥，K是P的一个子集．令Kr={x∈PC1[J,R]|‖x‖0．

定义算子TP→K，

笔者给出下面的假设：

(H1)假设对任意的r，r′>0，存在φ(t)∈L∞[0,1]，使得f(·,x1,x2)≤lφ(t)，其中(x1,x2)∈[0,r]×[0,r′],l=max{r,r′},t∈[0,1]．

其中，λ>0为一常数，

(H3)假设存在常数l0和b，其中

使得

为了方便，记

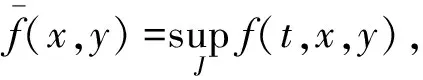
其中c>0,J=[0,1]．

引理6 假设(H1)、(H2)成立，那么TP→K是全连续算子，且T在P中的不动点是BVP(1)的一个正解．

证明很容易验证(Tx)″(t)≤0，所以Tx是非负、凹的．

第一步，证明对任意的x∈P,Tx∈K．

若0<α<1，根据引理4及T的定义，由(Tx)(η)=x(η),αx(η)=x(1)，以及(Tx)(1)=x(1)，所以(Tx)(η)≥(Tx)(1)．

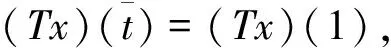
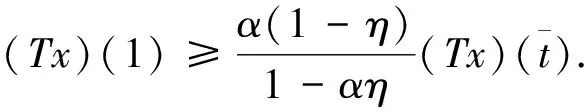
(2)

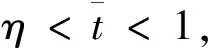
所以,由α(Tx)(η)=(Tx)(1)，得

即

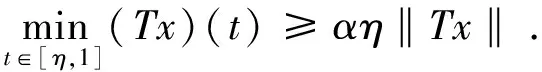
(3)

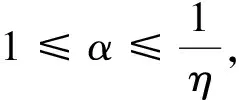
这与Tx的凹性矛盾．所以由(Tx)(η)≤(Tx)(1)及Tx的凹性知

这表明

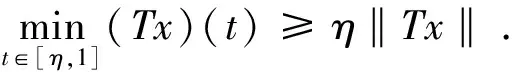
(4)

由式(2)～式(4)可知

接下来证明

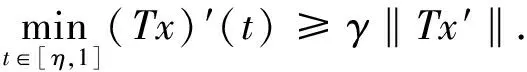
因为

所以

综上可知，TP→K．显然,如果x是T在P中的不动点,则x满足BVP(1)且是BVP(1)的一个正解．

第二步，证明T是全连续算子．

先证明T一致有界，假设S是D中的绝对有界集，即对任意的x∈S，

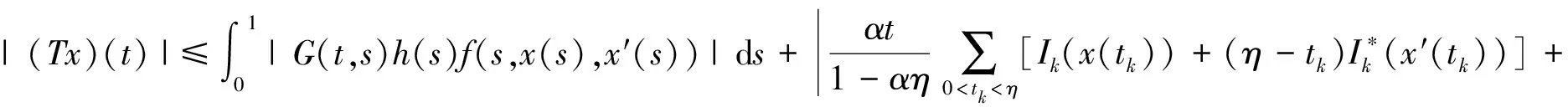
所以,T(S)中的诸函数及其导函数均在J上一致有界．

第三步，证明T在每个Jk(k=0,1,2,…,m)上等度连续．

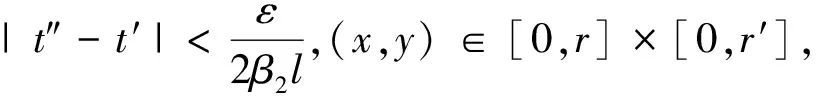
于是有

所以Tx在每个Jk(k=0,1,2,…,m)上等度连续．

由引理1，T(S)是相对紧集，又结合(H1)、(H2)，易知Tx连续，故TP→K是全连续算子．

综上可知，T在P中的不动点是BVP(1)的一个正解．证毕．

因此，由引理6的证明可知，T(K)⊂K．

2 主要结果

命题1 假设(H2)、(H4)成立，则存在r0>0，使得

i(T,Kr∩K,K)=1,∀r>r0.

证明由(H4)可知，存在r0>0，满足f(t,x,y)≤λ(‖x‖+‖y‖),x>r0或y>r0，t∈J.

又由(H2)知，对r0>0，存在φ(t)∈L∞[0,1]，使得

f(t,x,y)≤lφ(t),x,y∈[0,r0],t∈J.

因此对所有的x、y∈R+,t∈J，

f(t,x,y)≤λ(‖x‖+‖y‖)+lφ(t).

所以，令x∈Kr，使‖x‖=r>r0，

所以

‖Tx‖≤‖x‖,∀x∈∂Kr∩K.

由引理2中的2)，i(T,Kr∩K,K)=1．证毕．

命题2 假设存在c>0，有(H3)、(H5)成立，那么存在0

证明由(H5)知，存在0

取x∈Kρ，使得‖x‖=ρ，所以x∈∂Kρ∩K．

由(Tx)″(t)≤0,∀t∈J，有两种情形：

对第一种情形，

对第二种情形,

所以

‖Tx‖ ≥‖x‖,∀x∈∂Kρ∩K.

由引理2中的1)，i(T,Kρ∩K,K)=0．证毕．

下面的定理是本文的主要结果.

定理1 假设存在c>0，有(H1)～(H5)成立，那么BVP(1)至少有一个正解．

证明由(H4)和命题1知，存在r>0，使得i(T,Kr∩K,K)=1．由(H5)和命题2知，存在0<ρ

所以BVP(1)至少有一个正解．证毕．

定理2 假设(H1)～(H3)、(H6)成立，此外，假定存在ρ2>0，使得

f(t,x,y)≤m0ρ2,x,y∈[0,ρ2],t∈J.

其中

则BVP(1)至少有一个正解．

证明对x∈∂Kρ2，使得‖x‖∈ρ2，由命题1的证明，

所以

‖Tx‖≤‖x‖,∀x∈∂Kρ2∩K.

由引理2中的2)可知，i(T,Kρ2∩K,K)=1 ．

再由(H5)和命题2知，存在0<ρ