基于DRNN的非线性多变量系统控制算法

周瑞敏，周志青，喻 恒

(平顶山学院 信息工程学院，河南 平顶山 467036)

0 引言

随着工艺复杂性的增加和控制要求的提高，多变量耦合的非线性系统广泛存在于能源、化工、汽车、电网和电力电子等领域[1-5]，其控制器设计一直是学术和工程界长期面临的挑战和难题．

目前，针对多变量耦合系统的控制方法有基于数据的方法、鲁棒控制方法、自抗扰控制方法、预测控制方法、模糊控制方法和基于神经网络的方法等[6-9]．文献[6]通过增大控制输入差值周期，改进无模型自适应控制算法，在循环流化床锅炉燃烧过程模型中得到了仿真验证．文献[8]针对超临界机组燃水比耦合系统，把变量间耦合看作是单变量回路的一个干扰，设计了扩张状态观测器，用于实时估计，然后在每个回路构建了自抗扰控制器．文献[10]运用模糊逻辑PID控制方法对无人机姿态解耦，并且运用混沌优化理论对控制参数进行寻优．文献[11]利用多变量解耦内模控制(IMC)方法，设计了机组协调控制系统．文献[12]提出了一种基于DRNN解耦的控制参数在线自整定控制算法，并在某军用弹药仓库的温湿度控制系统中得到了仿真验证．

相对于其他方法，由于神经网络可以任意逼近非线性环节的优势，基于神经网络的方法处理多变量耦合非线性系统更具有优势[13-17]．文献[13]设计了基于遗传算法优化的PID神经网络解耦控制器，并在权值修正过程中引入了动量项．文献[14]针对双输入双输出的四容水箱系统，提出了基于小波神经网络的广义预测控制算法．

考虑到系统变量间的耦合作用及动量因子选取不当引起收敛过程中的震荡问题，笔者改进了优化PID参数的性能指标，并提出了一种自适应动量因子．

1 系统模型

考虑到被控对象中各个环节的非线性特性，并且各控制回路之间存在强耦合现象，数学模型可描述为式(1)：

(1)

其中，f1(u1(k-1),u2(k-1))、f2(u1(k-1),u2(k-1))为非线性函数，k、n均为正整数，k代表当前时刻，n为当前时刻之前第n时刻．

2 基于DRNN神经网络的自学习PID控制方法

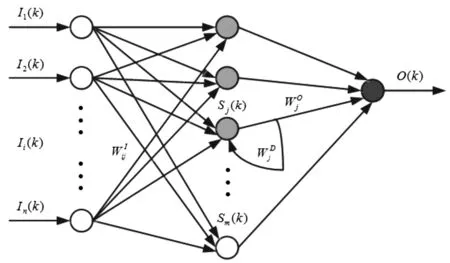
图1 DRNN结构

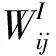
在控制过程中，已知给定参考值yr1(k)和yr2(k)，跟踪误差定义及控制方案原理图如图2所示,其中控制器部分包含两个子控制器，分别为PID控制器1和PID控制器2.两个控制器结构及原理相同，故只叙述PID控制器1的设计过程及参数意义，针对控制器2的相关叙述省略．

(2)

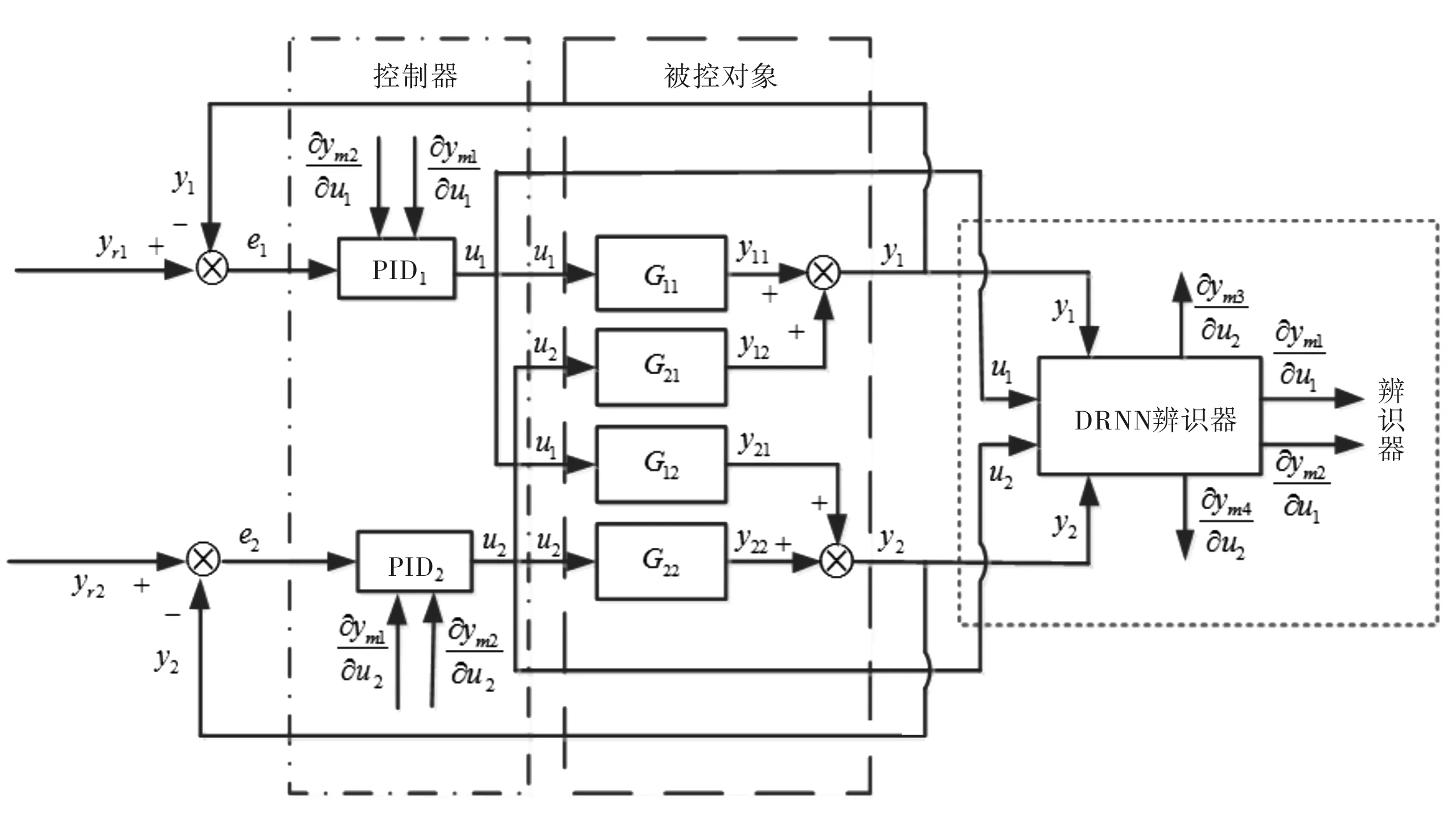
图2 控制方案原理

PID控制器根据跟踪误差按照如下控制律计算控制量:

(3)

式(3)中：kp1、ki1、kd1分别为PID控制器1的比例、积分和微分系数；T为采样周期；δp1(k)、δi1(k)、δd1(k)分别为误差、误差积分、误差微分．

为优化PID控制器1的参数值，采用梯度下降法进行调节，其优化性能指标如式(4)所示：

(4)

则控制器1参数调节律为：

(5)

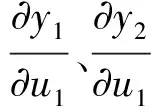
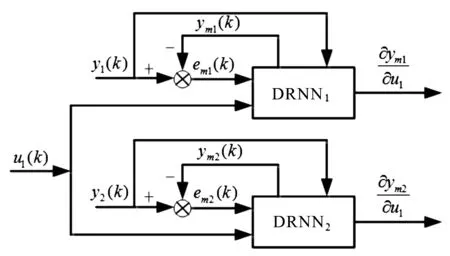
图3 辨识器1和2结构

图3中，y1(k)和u1(k)作为网络1的输入，ym1(k)作为网络1的输出，辨识误差em1(k)作为调整信号对网络权值进行调整，性能指标选取如下：

(6)

根据上述性能指标采用梯度下降法对神经网络权值进行更新，更新律如下：

(7)

为保证收敛过程中不出现震荡现象，设计自适应动量因子如下：

(8)

式(8)中，a、b为经验值，a可以控制收敛速度的快慢．则输入层权值更新律为：

(9)

式(9)中，ηI为输入层权值的学习速率，αI(k)为自适应动量因子，其他两层权值更新律类比可得．则上述PID控制器1参数计算过程中的雅可比信息可由以下公式得到：

(10)

式(10)中，WO为输出层权值，WI为输入层权值,g(*)为回归层的激活函数，笔者取双S函数．

3 仿真研究

为验证前述理论结果的正确性，选取如下多变量耦合非线性系统进行仿真验证：

(11)

本仿真实验在MATLAB环境下进行，实验迭代步数为5 000步，系统给定值为分段函数．部分仿真参数选取为：a=0.3，b=200；神经网络权值学习率均为：η=0.4；动量因子初始值均为：α=0.04．控制器参数初始值为：kp=0.1，kI=0.04，kd=0.2．

从图4和图5可以看出，随着给定值的变化，系统都能很好地跟踪给定值．在图6中，为了达到最佳控制性能，两个控制器参数在系统给定值发生变化时都进行了调节，并很快收敛到固定值．图7的4条曲线分别对应4个辨识器的雅可比信息，可以看出最终都随着系统的稳定收敛到了固定值．

图4 系统输出

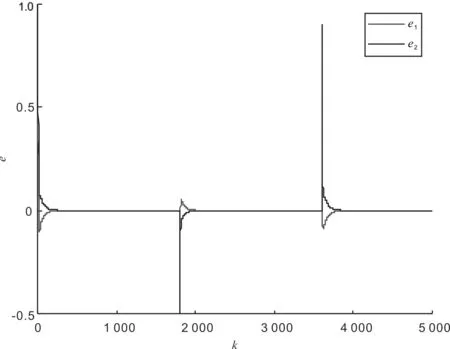
图5 系统误差

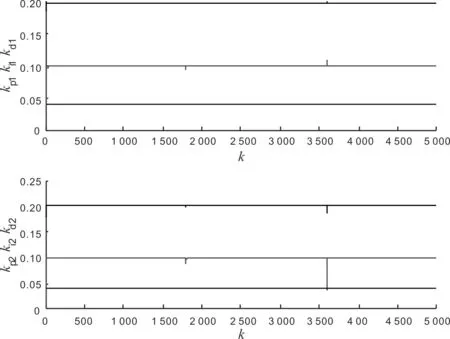
图6 控制器参数

图7 雅可比信息

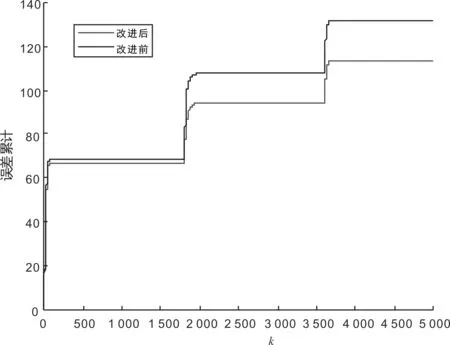
图8 误差累计对比

为了更好地说明笔者所提方法的优越性，与文献[18]中方法对比，选取跟踪误差累计作为对比性能指标，对比效果如图8所示.很明显，笔者所提的改进方法跟踪误差明显较小，达到了预期的效果．

4 结论

笔者提出了一种基于神经网络改进的PID自学习控制方法．具体地，主要给出了改进的PID参数优化指标和自适应动量因子，为了验证所提方法的有效性，选取了双输入双输出的非线性系统进行仿真验证，随着给定值的变化，系统输出都能快速跟随上给定值，相应的控制器参数也很快收敛到稳定值，最后通过对比实验验证了方法的优越性．