二阶系统测速反馈控制的n次方型变阻尼技术研究

许曼儿 邓展豪 陈丽芬 许日雄 肖红军

二阶系统测速反馈控制的次方型变阻尼技术研究

许曼儿 邓展豪 陈丽芬 许日雄 肖红军

（佛山科学技术学院机电工程与自动化学院，广东 佛山 528000）

在二阶系统测速反馈控制的变阻尼技术中，传统的线性变阻尼和平方型变阻尼关系式动态性能存在一定的优化空间。在研究变阻尼传统数学表达式的基础上，引入新参数，提出一种二次分段的次方型变阻尼关系式。经仿真验证，在参数相同的情况下，二次分段的次方型变阻尼关系式改善了系统动态性能。

二阶系统；变阻尼；非线性；误差泛函积分指标

0 引言

在二阶系统测速反馈控制中，固定阻尼比无法同时兼顾动态性能和稳态性能[1-2]。采用变阻尼控制技术，使系统在输出响应的不同阶段具有不同的阻尼比，能同时兼顾快速性与稳定性。

目前，对二阶系统测速反馈控制的变阻尼技术研究主要分为2类：第一类是优化变阻尼数学关系式的数学模型，包括分段变阻尼、线性变阻尼、平方关系变阻尼；第二类是主要以模糊控制为主的智能变阻尼技术。第一类变阻尼控制技术比较单一、鲁棒性较差，但实现简单；第二类变阻尼控制技术的智能控制存在模糊规则设置复杂、难以应用的问题[3-5]。

本文研究第一类变阻尼关系式，提出一种二次分段的次方型变阻尼关系式，优化系统动态性能、抗干扰性能，且实现更加简单。

1 二阶系统特性分析

单位反馈二阶系统的开环传递函数为

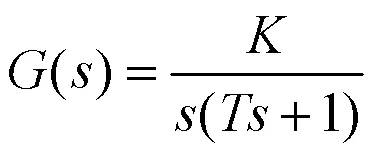
闭环传递函数为

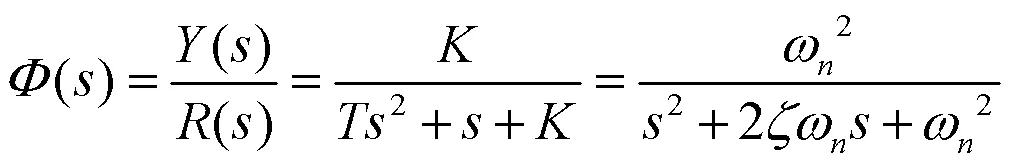
典型二阶系统的特征方程为

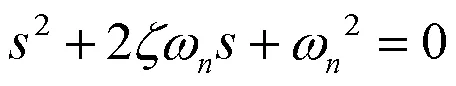
特征方程的根为

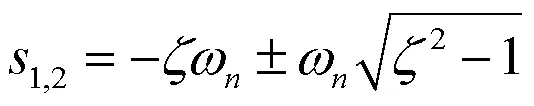
本文采用误差泛函积分指标中的时间乘绝对误差积分指标来衡量系统的响应过渡过程，表达式为

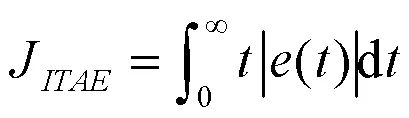
指标值越小，误差越小，动态性能越好。

2 n次方型变阻尼控制

变阻尼控制系统结构图如图1所示。通过调整系统的输出偏差()，在线调整测速反馈通道增益k，从而改变系统的阻尼比。

在快代谢组46例中，有2例换用替格瑞洛，没有发生心血管缺血事件；在44例继续口服氯吡格雷的患者中，17例再发心绞痛，其中2例再次靶血管重建。

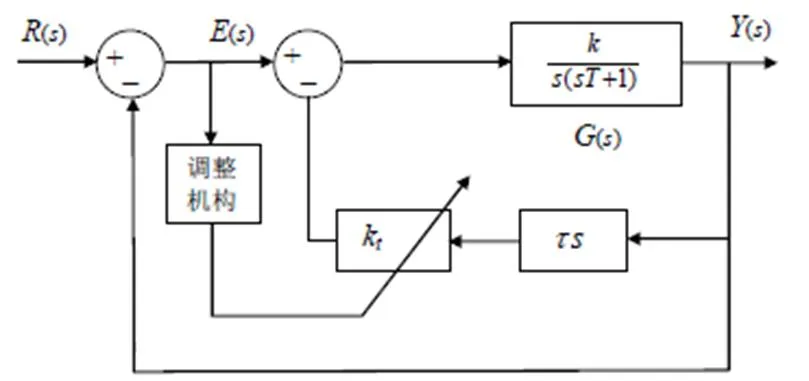
图1 变阻尼控制系统结构图

一次分段的线性变阻尼关系式[1]为

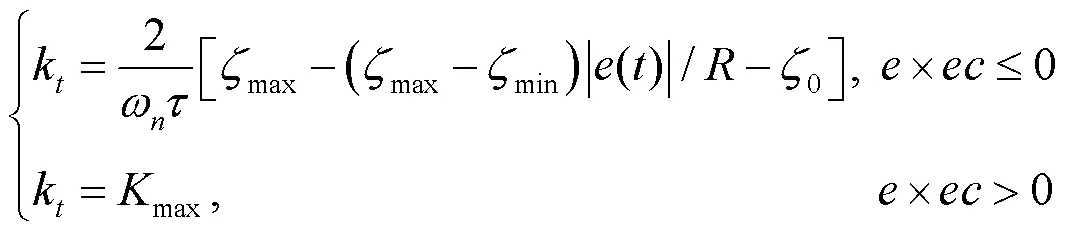
当系统处于稳态时加干扰信号，变阻尼控制抗干扰仿真结果如图2所示。其中，曲线1为固定阻尼比为0.707的阶跃响应曲线；曲线2为采用变阻尼抗干扰措施后系统的仿真曲线；曲线3是幅值为0.2的干扰脉冲。

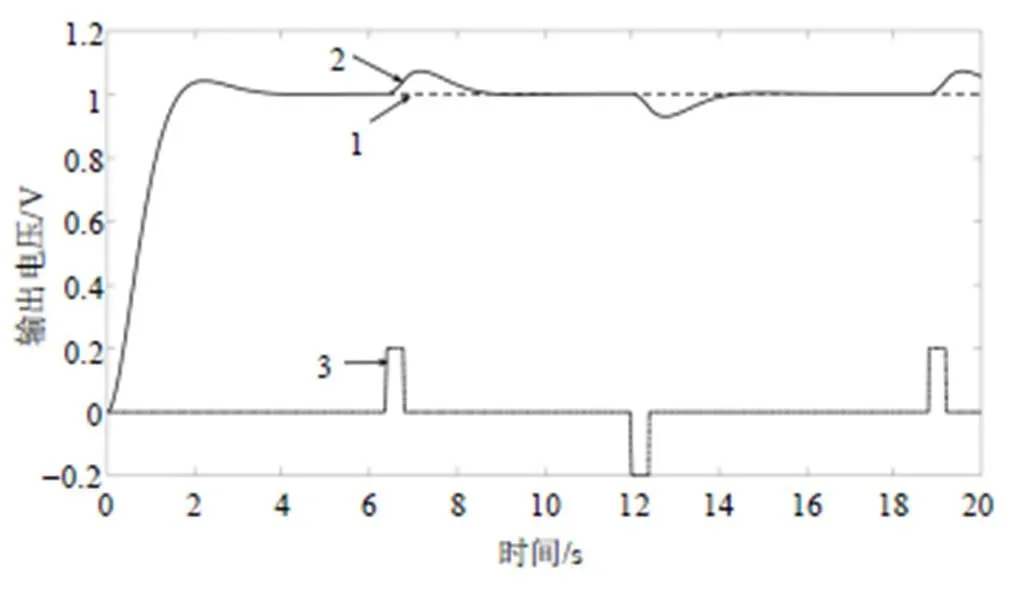
图2 变阻尼控制抗干扰仿真结果

图2仿真结果说明，变阻尼抗干扰措施有效。

在一次分段的线性变阻尼关系式的基础上[1]，研究一次分段的次方型非线性变阻尼关系式：

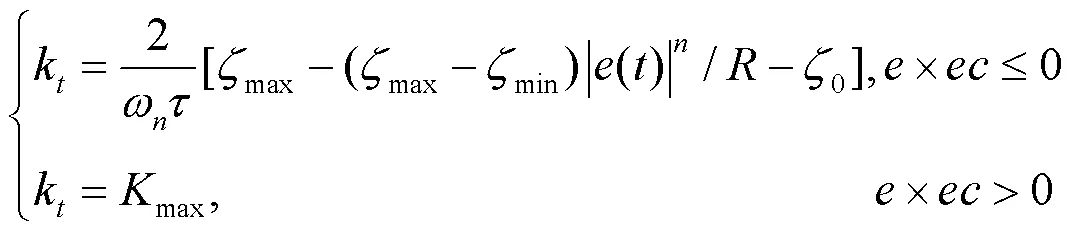
当越趋于0时，响应速度越快，超调越大，但稳定于终值后抗干扰性越强；当越趋于1时，响应速度越慢，超调越小，稳定于终值后抗干扰性越弱。仿真模型如图3所示。

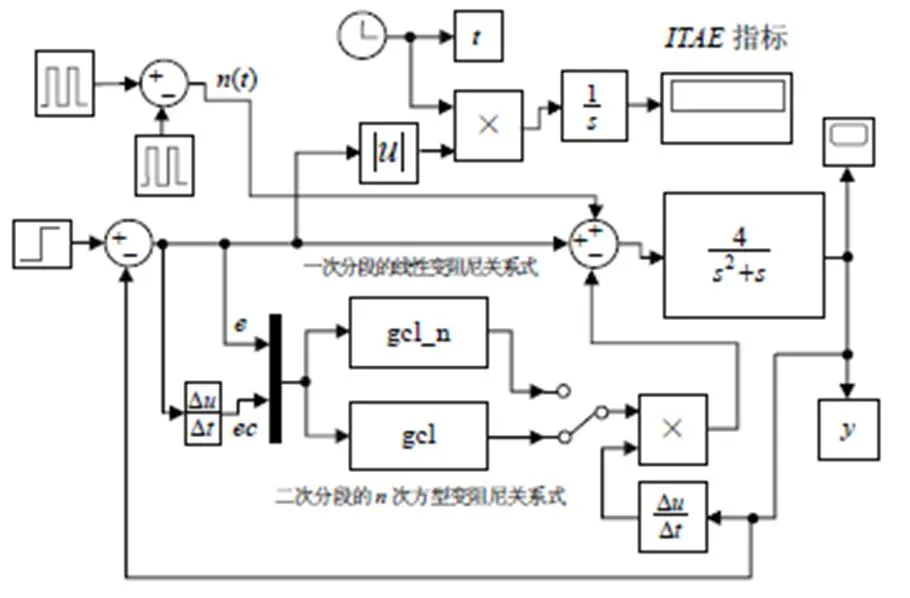
图3 非线性变阻尼控制系统仿真模型

= 0.75和= 1（线性变阻尼关系式）时的响应曲线如图4所示。相比于= 1，= 0.75的响应曲线上升时间明显缩短，但两者抗干扰能力几乎相同。同时，当= 0.75时，具有不可避免的超调量，此处为0.06%，超调量在合理范围内。实际生产中，应根据实际系统选取值。

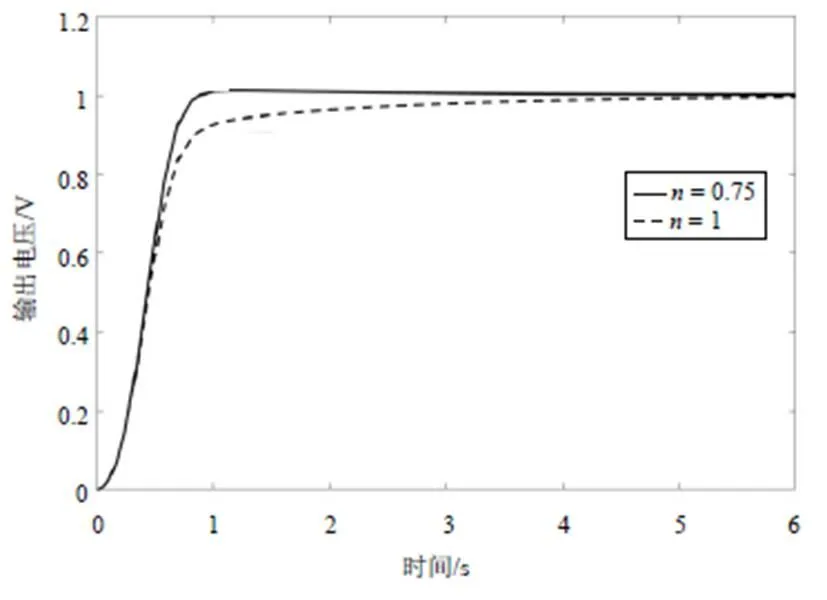
图4 n = 0.75和n = 1的响应曲线

当= 0.000 1和= 0.75时的响应曲线如图5所示。相比于= 0.75，= 0.000 1时系统受到干扰后恢复稳定值的时间较短，抗干扰性能更好，但超调量较大。3个典型参数的仿真结果如表1所示。

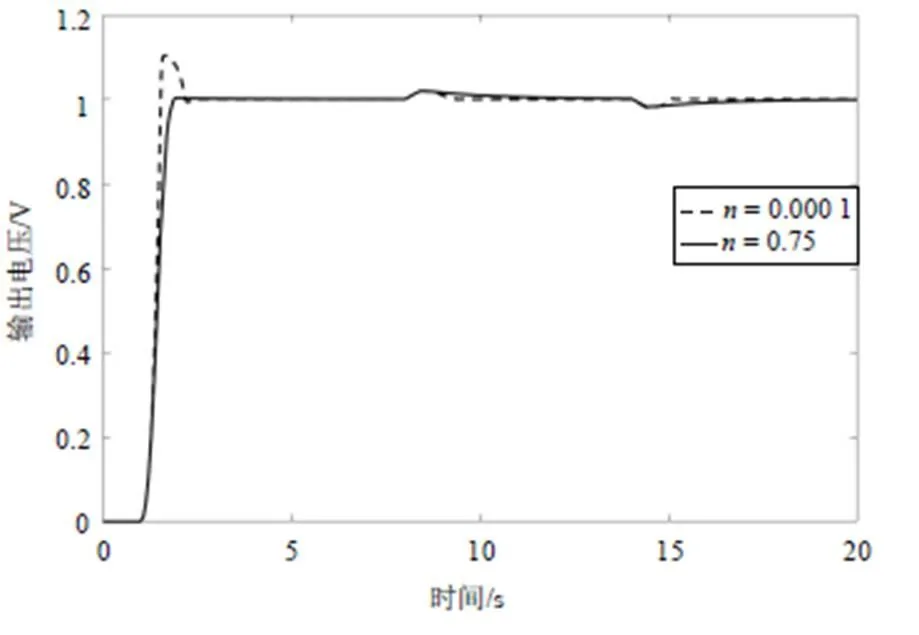
图5 n = 0.000 1和n = 0.75的响应曲线

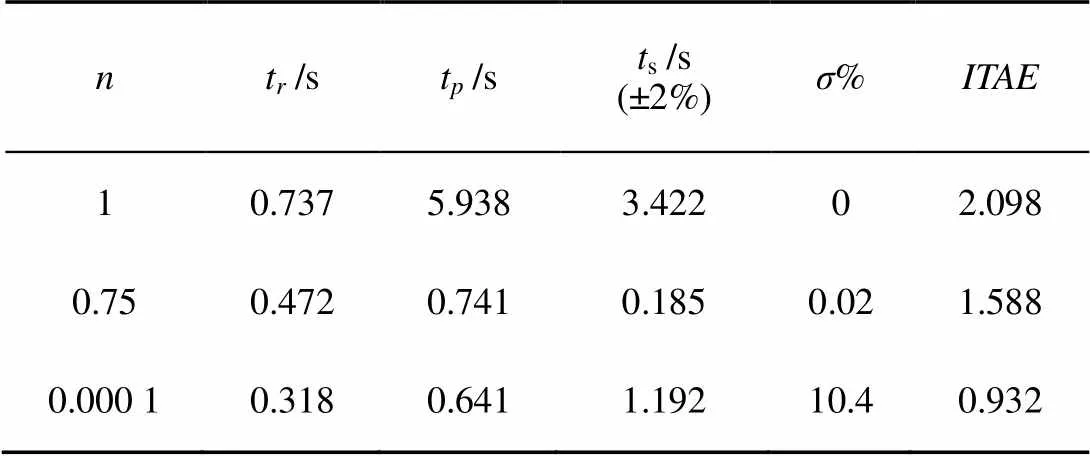
表1 一次分段的n次方型变阻尼仿真结果

注：为次方型变阻尼关系式的参数；t为上升时间；t为峰值时间；t为调节时间；%为超调量；为误差泛函积分指标。

由表1可知，= 0.000 1的上升时间最小，抗干扰能力最好，但超调量却很大。

3 二次分段的n次方型变阻尼控制

为结合= 0.000 1和= 0.75两者的优势，提出二次分段的次方型变阻尼关系式，其中根据响应终值()，设定阈值为= 0.02×(∞)。

在实际生产中，根据允许的超调量，可按需取阈值为其他值。

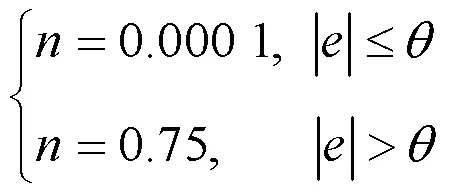
式(6)与式(7)共同组成二次分段的次方型变阻尼关系式。

4 实验验证

为验证二次分段的次方型变阻尼控制效果，分别对模糊控制变阻尼技术、二次分段的次方型变阻尼关系式、一次分段的线性变阻尼关系式3种情况进行仿真[6-8]。其中，归一化后的模糊输入量论域为[1，−1]，模糊输出量论域为[−1，2]。在Matlab环境下，对比仿真效果如图6所示，3种变阻尼技术仿真结果对比如表2所示。

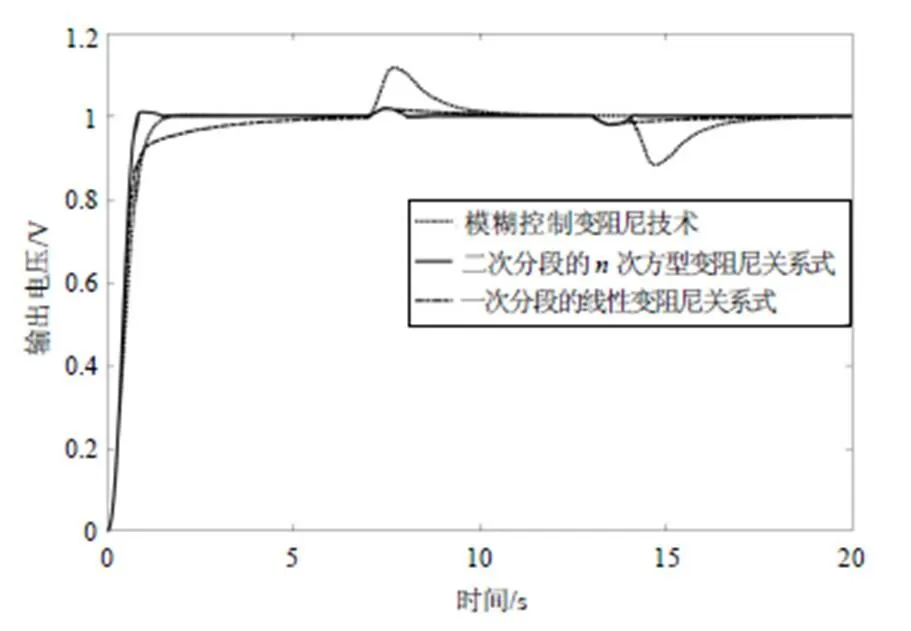
图6 3种变阻尼技术的仿真结果

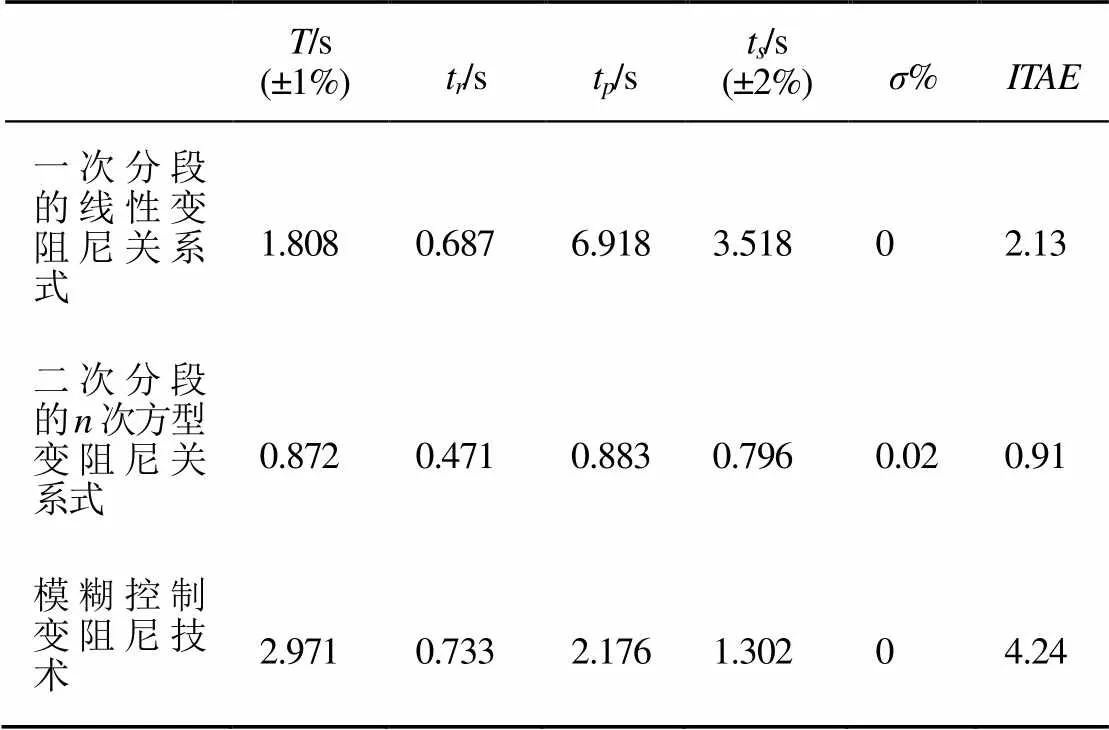
表2 3种变阻尼技术仿真结果对比

由图6可以看出，在一次分段的线性变阻尼关系式的基础上，不改变原来参数情况下，添加二次分段和参数后的新型变阻尼关系式的动态性能、抗干扰性能有较大提高，且参数的复杂性几乎不变。

由表2可看出：二次分段的次方型变阻尼关系式受到干扰时，恢复时间= 0.872 s，上升时间t= 0.471 s，调节时间t= 0.796 s，均比一次分段的线性变阻尼关系式和模糊控制变阻尼技术的时间更短；误差泛函积分指标也得到明显改善。表明二次分段的次方非线性变阻尼控制技术能有效改进二阶系统测速反馈控制的动态性能、抗干扰性能，并且参数简单易设置。

相对于线性变阻尼关系式而言，采用二次分段的次方型变阻尼关系式，指标从2.13降低到0.9109，缩短了上升时间与调节时间，并且受到干扰时能快速恢复稳定值，兼顾了快速性与稳定性。

模糊控制变阻尼技术可能具有更高的改善系统性能上限，但受限于模糊规则设置的复杂程度，实际设计中对技术要求较高。

5 结论

首先，本文分析了二阶系统测速反馈控制的线性变阻尼关系式、分段变阻尼关系式；然后，在线性变阻尼关系式的基础上，通过引入新参数，提出了二次分段的次方型变阻尼关系式；最后，建立Matlab仿真模型并进行仿真分析。仿真结果表明：在不修改线性变阻尼关系式原有参数的情况下，新引入参数，结合分段的方法控制阻尼变化，可明显优化二阶系统测速反馈控制的动态性能。

[1] 龚昌来.变阻尼控制技术改善二阶系统性能的研究[J].自动化技术与应用,2004,23(9):21-23.

[2] 龚昌来.二阶系统模糊变阻尼技术[J].机电工程技术,2004, 33(7):86-87,100.

[3] 王清,马克茂.不确定非线性系统的非光滑控制及应用[J].自动化与信息工程,2013,34(3):1-6.

[4] 王志平,谢运祥,王裕.基于反馈控制的矩阵整流器研究[J].自动化与信息工程,2013,34(1):34-40.

[5] 代慧,朱洪雷.互相关与阻尼比扰动混沌系统结合的检测方法[J].自动化与信息工程,2011,32(2):18-20.

[6] 王淯舒,孙培德,吕蕾.基于自整定模糊PID控制的Buck变换器设计与仿真[J].自动化与信息工程,2014,35(5):39-45.

[7] 范晓英,陆培新,陈文楷.一个新型的模糊控制器[J].控制理论与应用,1995(5):597-602.

[8] 胡国亮,陈久康.用MATLAB进行模糊控制器的设计和仿真[J].基础自动化,2000(1):15-20.

Research on-th Power Variable Damping Technique for Velocity easurement Feedback Control of Second-order Systems

Xu Maner Deng Zhanhao Chen Lifen Xu Rixiong Xiao Hongjun

(College of Mechanical and Electrical Engineering and Automation, Foshan University, Foshan 528000, China)

In the variable damping technology of speed measurement feedback control for second-order systems, there is a certain optimization space for the dynamic performance of the traditional linear variable damping and square variable damping relations. Based on the study of the traditional mathematical expression of variable damping, a quadratic piecewise-th power variable damping relationship is proposed by introducing new parameters. The simulation results show that the quadratic piecewise-th power variable damping relationship improves the dynamic performance of the system under the same parameters.

second order system; variable damping; nonlinear; error integral functional index

许曼儿，女，1998年生，本科生，主要研究方向：智能电网技术。

邓展豪，男，1999年生，本科生，主要研究方向：智能检测与智能控制。

陈丽芬，女，1998年生，本科生，主要研究方向：智能电网技术。

许日雄，男，1999年生，本科生，主要研究方向：智能检测与智能控制。

肖红军，男，1979年生，博士，副教授，主要研究方向：智能检测与智能控制。E-mail: jinsery@163.com

TP13

A

1674-2605(2021)05-0009-04

10.3969/j.issn.1674-2605.2021.05.009