基于改进DDPG算法的船舶航迹跟随控制系统*

余凡 蒋晓明 张浩 曹立超 周勇 刘晓光　

基于改进DDPG算法的船舶航迹跟随控制系统*

余凡 蒋晓明 张浩 曹立超 周勇 刘晓光

（广东省科学院智能制造研究所，广东 广州 510070）

鉴于船舶在航行时受到风、浪和流等不确定因素干扰，传统的船舶航迹控制方法难以在不确定环境且控制系统处于多输入、多输出的条件下精确建模，导致船舶容易偏离预设航迹，影响船舶行驶的安全性。为降低船舶偏航，实现船舶航迹的精准控制，将深度确定性策略梯度（DDPG）算法引入到控制系统。首先，分析船舶的运动学，详细介绍DDPG算法的基本原理并对算法进行改进；然后，在Matlab/Simulink中搭建船舶航迹跟随控制系统并进行仿真实验。实验结果表明，该系统稳定性好，能对外部干扰迅速做出响应，对船舶航迹控制具有一定的参考价值。

DDPG算法；航迹跟随；船舶控制系统

0　引言

在经济全球化的影响下，船舶行业的贸易占据了重要地位。随着船舶运动控制技术的不断完善，船舶行业朝着大型化、专业化、数字化和货物种类多样化方向发展。船舶相关技术的研究得到广泛关注，其中研究重点之一就是船舶运动控制自动化水平的提高[1]。船舶运动控制分为手动控制和自动控制[2-4]，手动控制对操作者的经验要求较高，不利于船舶在环境多变的海洋上航行，目前已形成自动控制代替手动控制的趋势。自动控制实现了航向和航迹保持[5]、航速控制[6-7]等功能，在提高船舶运动控制智能化[8-9]的同时，可以减少偏航次数、航向偏差；并在保证经济效益的同时，提高船舶和船员的安全性[10]。

船舶运动控制的核心问题是如何不断地改进控制策略，以保证在有干扰的环境下及船舶本身存在动态特性改变的情况下，仍能满足航运性能指标要求。由于船舶在航行中会受到风、浪和流的影响，且船舶控制系统为多输入多输出的动力学系统，在气候、水文、航道等不确定的外部因素和负载、动力等内部因素的影响下，无法建立准确的数学模型。采用端到端强化学习的方式[11]，不需要复杂的控制器，黑箱控制即可处理连续状态空间并输出连续的动作，可解决船舶控制模型难以精确建模的问题[12]。

本文在传统的船舶航迹跟随控制系统中引入深度确定性策略梯度（deep deterministic policy gradient, DDPG）算法，并把船舶航迹跟随控制系统建模成马尔可夫决策过程；改进DDPG算法，离线学习训练船舶航迹跟随控制系统；在Matlab/Simulink中搭建船舶航迹跟随控制系统并进行仿真实验，验证DDPG算法的有效性。

1 船舶航迹跟随控制系统设计

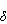
图1 船舶航迹保持方式

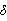
船舶航行时，船舶航迹跟随控制系统会产生大量参数整定和复杂计算等问题，系统鲁棒性较差。为保证船舶航迹跟随的实时性，本文采用间接式航迹保持控制方式，并将DDPG算法引入控制系统，如图2所示。

图2 间接式航迹保持控制系统框图

2　船舶运动学分析

船舶航行时具有6个自由度，其中前进、横漂和起伏为3个平移自由度；转艏、横摇和纵摇为3个转动自由度。惯性坐标系与附体坐标系平面示意图如图3所示。

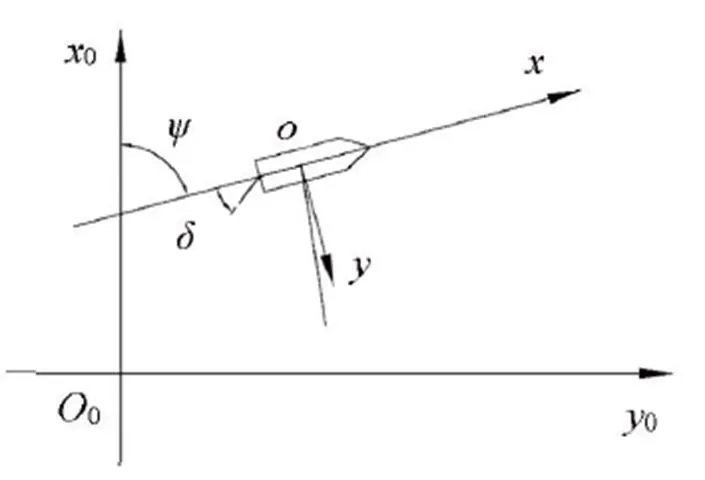
图3 惯性坐标系与附体坐标系平面示意图

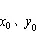
由图3可知，船舶在2个坐标系间的运动学关系可表示为

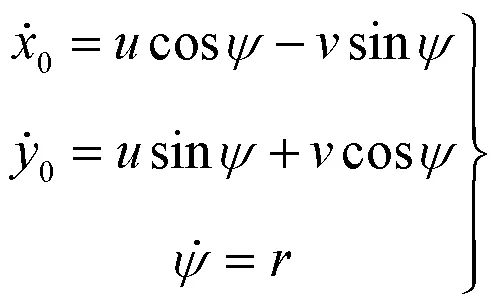
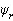
3 DDPG算法

3.1　马尔可夫决策过程

强化学习中智能体的动作取决于环境信息的反馈，同时受回报值的影响，朝回报最大化的方向寻找当前环境下智能体能达到预期效果的动作。其中，智能体是学习及实施决策的机器，与智能体相互作用的其他对象都被称为环境（即船舶）。智能体需具备学习能力且能够在某种程度上感知环境状态，并采取动作影响环境状态，如图4所示。

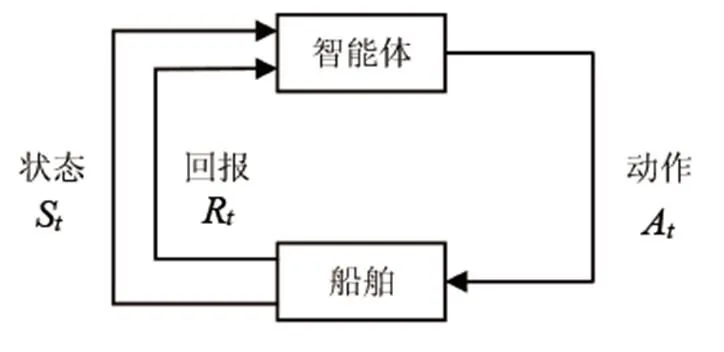
图4 马尔可夫决策过程的智能体-船舶交互

图4中智能体的动作可以是任何决策，而状态则是船舶的位置、速度、外界干扰等反馈信息。在智能体与船舶进行信息交互前，不需要确定控制模型中具体参数值，可通过离线学习的方式收敛到最优值。

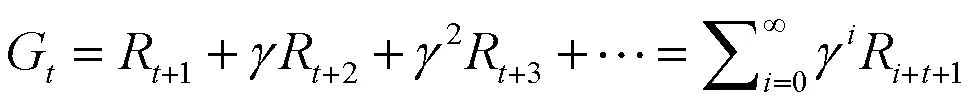
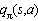
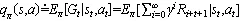
对函数的动作函数进行加和，即可得到价值函数：

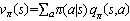
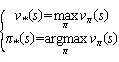
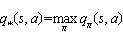
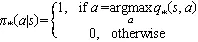
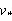
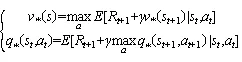
由于使用学习在状态量较大或连续任务中，会遇到维度灾难问题，本文在强化学习中利用价值函数近似的方法可以解决该问题。本文引入Deep Q Network（DQN）的概念，其基于Q_learning算法，加入价值函数近似于神经网络，采用目标网络和经验回放的方法进行网络训练，并从历史数据中随机采样，以最小化样本之间的相关性。

在强化学习算法中，智能体的策略用神经网络表示。在此引入执行器和评价器2个概念。其中，执行器表示在基于策略函数的学习算法中，以状态为输入，以动作为输出，对神经网络进行训练。此时的神经网络不仅代表智能体的策略，也称为执行器，其参数用来表示，如图5所示。策略函数算法虽然能够处理连续的动作空间，但会出现测量噪声大，不能收敛的情况。

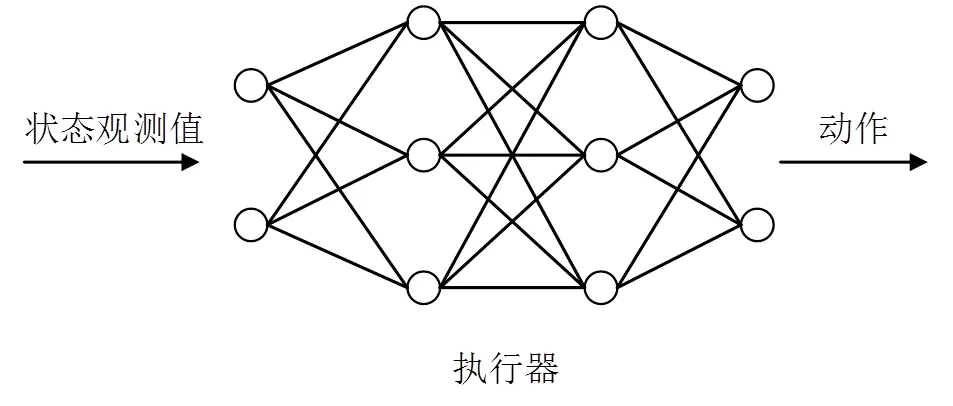
图5 基于策略函数的学习

评价器在基于价值函数的学习算法中，以状态和当前状态下的动作为输入，由神经网络返回状态动作对的价值，此时的神经网络被称为评价器，其参数用表示，如图6所示。

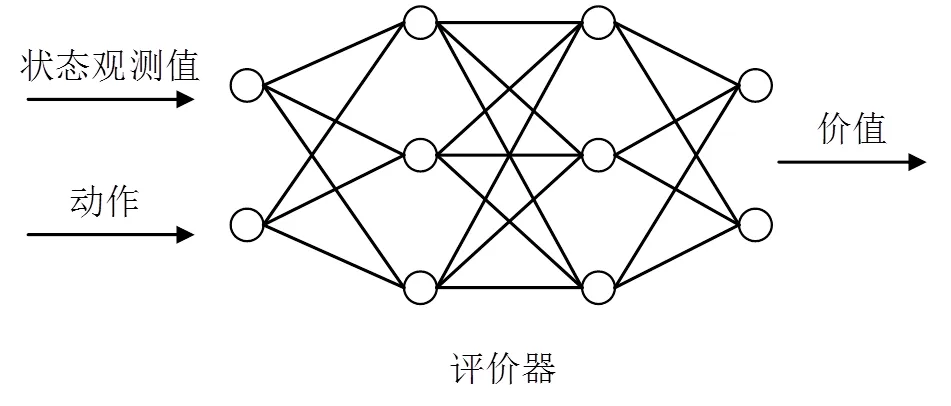
图6 基于价值函数的学习

3.2　改进DQN算法

由图6可知，神经网络输出的是价值，并不能用来表示策略，将执行器和评价器合并成一个算法，即执行器-评价器算法，如图7所示。

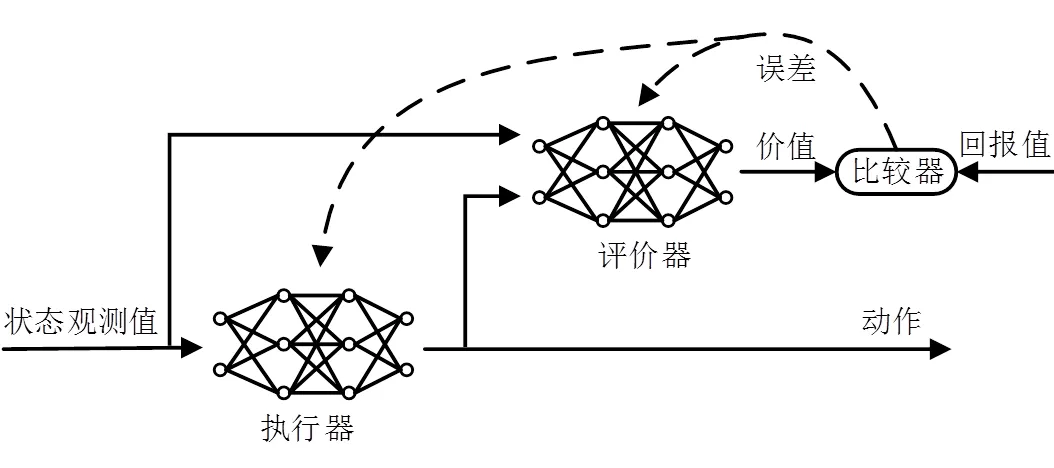
图7 执行器-评价器算法

执行器-评价器算法中的执行器能够处理连续动作空间，评价器只需根据当前状态和执行器输出的动作来预测对应的价值，进而将此价值与环境所返回的奖励进行比较；得到的误差用来评判当前状态下采取动作时，环境中的奖励是否高于预测的价值。此误差也用于对评价器和执行器进行反馈，使2个神经网络自我更新，调整执行器输出的动作。因此，执行器-评价器算法能够处理连续的状态和动作空间，并能在环境返回奖励方差较大时加快学习速度。

针对以上SOC估算的影响因素,本课题组进行了锂离子电池SOC估算的相应实验。实验以两组锂离子电池组为研究对象,每组电池组用3片锂离子电池串联而成,单体电池型号为INCMP58145155N-I,额定电压为3.7 V,额定容量10 Ah。具体的实验过程为将两组电池组每天先进行从10%～70%的深度放电,记录回跳电压,并搁置2 h,待电压恢复后,再进行 0.2 C 完全放电。每当放电深度设置的一个实验周期结束,改变放电倍率重复实验。并且分别置两组电池于高温和低温环境下,以观测环境温度对电池剩余容量的影响。实验采用蓄电池综合参数自动测试设备,型号为BTS-M 300 A/12 V。

3.3　DDPG算法在控制系统中的应用

DDPG算法是一个基于神经网络函数近似器并且可以在高维的、连续动作空间中学习策略的无模型、执行器-评价器离轨策略算法。其中，神经网络函数近似器是通过对DDPG算法所使用的非线性函数近似器进行修改得到的。DDPG算法将actor-critic方法和DQN相结合。在每个批次的学习中，需要分别对评价器和执行器进行更新。

评价器更新考虑到Q_learning是一个无策略算法，

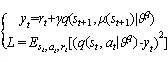
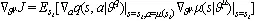
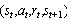
DDPG算法的整体流程如图8所示。

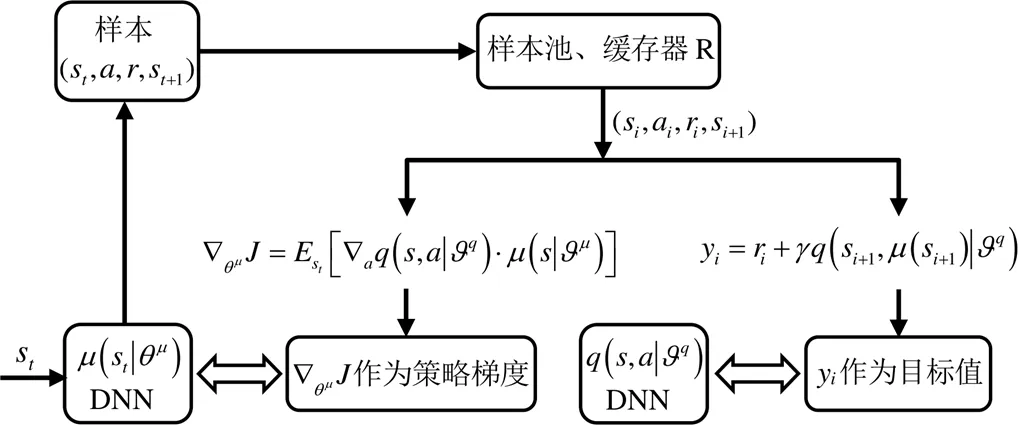
图8 DDPG算法流程图

4 控制系统仿真实验

为验证本系统的可行性，在Matlab/Simulink中搭建船舶航迹跟随控制系统，并采用常规小型船作为控制对象。为保证仿真效果更接近实际环境，在仿真环境中加入低频和高频干扰，模拟风、浪和流对船舶产生的影响；并设定操作舵的最小时间间隔为3 ～5 s，与实际船舶航行时自动舵的调整间隔保持一致。基于DDPG算法的船舶航迹控制效果如图9所示。

由图9可以看出，本文提出的基于DDPG算法的船舶航迹跟随控制系统能够达到较好的轨迹跟踪效果，且控制效果稳定，具有良好的鲁棒性。

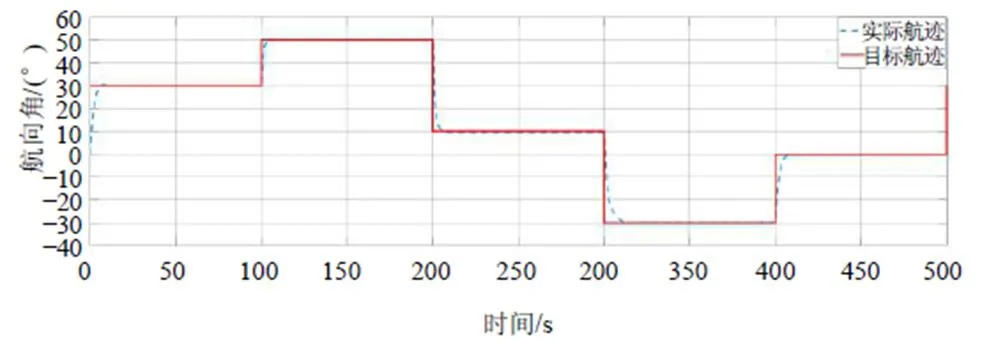
图9 航迹控制效果

5　结论

本文针对船舶航行时，容易偏离规划的航迹路线，航迹跟踪效果较差等问题，提出一种基于DDPG算法的船舶航迹跟随控制系统。首先，对船舶的运动学进行分析，并给出强化学习算法的推导过程；然后，在Matlab/Simulink搭建船舶航迹跟随控制系统，完成船舶航迹跟踪的仿真实验。从实验结果可以看出，该控制系统稳定性好，能对外部干扰迅速做出响应。

[1] 张显库.船舶控制系统[M].大连:大连海事大学出版社,2010.

[2] 侯志强.单片机船舶导航自动控制系统[J].舰船科学技术,2021,43(4):106-108.

[3] 韩春生,刘剑,汝福兴,等.基于PID算法的船舶航迹自动控制[J].自动化技术与应用,2012,31(4):9-12.

[4] 冯哲,张燕菲.基于PID算法的船舶航迹自动控制方法[J].舰船科学技术,2018,40(12):34-36.

[5] 祝亢,黄珍,王绪明.基于深度强化学习的智能船舶航迹跟踪控制[J].中国舰船研究,2021,16(1):105-113.

[6] 储琴,夏东青.PID控制在船舶自动定位中的应用[J].舰船科学技术,2020,42(18):88-90.

[7] 张晓兰,王钦若,时丽丽.动力定位船舶纵向运动的反步法控制器设计[J].自动化与信息工程,2011,32(5):1-4.

[8] 刘建圻,曾碧,郑秀璋,等.基于S3C2440的嵌入式导航平台的设计与实现[J].自动化与信息工程,2008,29(2):1-3,13.

[9] 邹木春,曾应坚.基于机器视觉的船舶升沉检测方法[J].自动化与信息工程,2010,31(3):37-39.

[10] 潘为刚,肖海荣,周风余,等.小型船舶自动操舵控制系统的研制[J].船海工程,2009,38(1):68-70.

[11] Richard S Sutton, Andrew G Barto. Reinforcement learing: an introduction[M]. MIT Press, Bradford Books, 1998.

[12] LILLICRAP T P, HUNT J J, PRITZEL A, et al. Continuous control with deep reinforcement learning[J]. Computer Ence, 2015.

Ship Track Following Control System Based on Improved DDPG Algorithm

Yu Fan Jiang Xiaoming Zhang Hao Cao Lichao Zhou Yong Liu Xiaoguang

(Institute of Intelligent Manufacturing, GDAS, Guangzhou 510070, China)

Since the ship is disturbed by uncertain factors such as wind, wave and current, the traditional ship track control method is difficult to accurately model in the uncertain environment and the control system is in the condition of multi input and multi output, which leads to the ship easy to deviate from the preset track and affects the safety of ship driving. In order to reduce ship yaw and realize accurate control of ship track, depth deterministic strategy gradient (DDPG) algorithm is introduced into the control system. Firstly, the kinematics of ship is analyzed, the basic principle of DDPG algorithm is introduced in detail, and the algorithm is improved. Then, the ship track following control system is built in Matlab/Simulink and the simulation experiment is carried out. The experimental results show that the system has good stability, can respond quickly to external interference, and has a certain reference value for ship track control.

DDPG algorithm; track following; ship control system

余凡，男，1996年生，硕士，助理工程师，主要研究方向：机电一体化。E-mail: f.yu@giim.ac.cn

蒋晓明，男，1973年生，博士，研究员，主要研究方向：电力电子、数控技术与自动化。E-mail: xm.jiang@giim.ac.cn

张浩，男，1993年生，硕士，助理工程师，主要研究方向：机器人与自动化。E-mail: h.zhang@giim.ac.cn

曹立超，男，1990年生，硕士，工程师，主要研究方向：机器人设计与自动化。E-mail: lc.cao@giim.ac.cn

周勇，男，1991年生，硕士，工程师，主要研究方向：计算机视觉。E-mail: y.zhou@giim.ac.cn

刘晓光，男，1980年生，硕士，副研究员，主要研究方向：机器人焊接技术。E-mail: xg.liu@giim.ac.cn

基金项目：广东省海洋经济专项项目（GDNRC[2021]024）

U664.82

A

1674-2605(2021)05-0004-06

10.3969/j.issn.1674-2605.2021.05.004