区块链技术中高效散列函数的设计与实现
滕飞, 李永珍
( 延边大学 工学院, 吉林 延吉 133002 )
0 引言
区块链技术由于具有能保障避数据安全、提高协同效率和控制风险等优点,因此其在数字货币、智能合约、供应链管理、物联网金融等方面得到应用[1-2].但随着区块链技术的广泛应用,现有的区块链技术在处理数据的效率方面逐渐难以满足人们的要求,因此提高区块链技术处理数据的效能具有重要意义.针对区块链中的哈希函数计算效率较低进而影响区块链整体计算效率的问题,文献[3]提出了一种基于FPGA的区块链哈希加速优化算法,但文献的作者并未对该优化算法的安全性方面进行说明.文献[4]对SHA - 2系列算法进行了改进,改进后的算法的安全性虽然比原算法有所提高,但其效率与原算法基本相同.基于上述研究,本文针对SHA - 256的迭代结构进行改进,并通过效率测试实验和雪崩效应实验验证了改进后的SHA - 256算法可有效提高区块链的效率和安全性.
1 相关技术简介
1.1 区块链中的数据结构
区块链中的数据结构通常由区块头(块头)和区块体(块身)组成,如图1所示[5].区块头一般包括版本号、前一区块的Hash值(Hash指针)、随机数、目标Hash值(本区块的Hash值)、Merkle根等.区块体保存的是若干条记录以及由每条记录的Hash值构成的二叉Merkle树[6].由于哈希函数具有单向性、抗碰撞性等特点,因此其目前被广泛应用于区块链技术中.哈希算法在区块链技术中的主要作用是将一个交易区块中的交易信息转换成一个哈希值(区块链通过比对交易信息的哈希值来确定信息有无被篡改),以及用于数据加密、共识计算的工作量证明、区块之间的链接等[7-9].
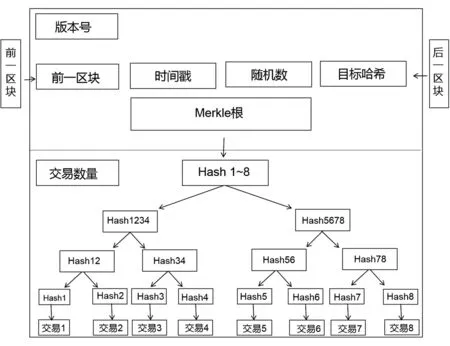
图1 区块数据结构图
1.2 SHA - 256算法
传统的SHA-256算法是将任意长度的字符串压缩成固定长度的字符串的一种算法.该算法的压缩过程为:首先利用一种不可逆的方式将接收到的一段明文转化为一段长度较短、位数固定的散列值,然后通过处理明文生成一个256 bit长的哈希值(消息摘要),最后通过比对哈希值确定信息是否被篡改[10].
SHA-256算法的加密过程如下:
第1步 初始化常量.初始化常量包括8个哈希初值(如表1所示)和64个哈希常量.

表1 SHA - 256算法的哈希初值
第2步 信息处理.信息处理的方式是在报文末尾对数据进行填充.填充方法是:补充第1个比特,为数字1; 剩余的比特数补充数字0.填充的结果是报文长度对512取模以后的余数为448.
第3步 计算消息摘要.本文采用函数迭代的方式计算消息摘要,由此共生成64个字.其中前16个字(记为w[0],…,w[15])由块分解(将消息分解成512 bit大小的块,每个字的大小为32 bit[11])产生,其余48个字由迭代公式得到.迭代公式[12]为:
Wt=σ1(Wt -2)+Wt -7+σ0(Wt -15)+Wt -16.
SHA - 256算法中的映射函数一共包含64次加密循环次数,如图2所示.在图2中:ABCDEFGH这8个字(word)按照一定的规则进行更新,其初始值分别为h0、h1、h2、h3、h4、h5、h6、h7;Kt对应的是64个常量;Wt是本区块产生的第t个字.对ABCDEFGH这8个字进行循环加密的过程中,最后一次循环所产生的8个字合起来即是第i个块对应到的散列字符串.SHA - 256算法中的逻辑运算如表2所示.
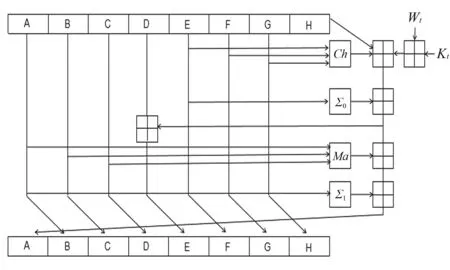
图2 映射函数的加密循环示意图
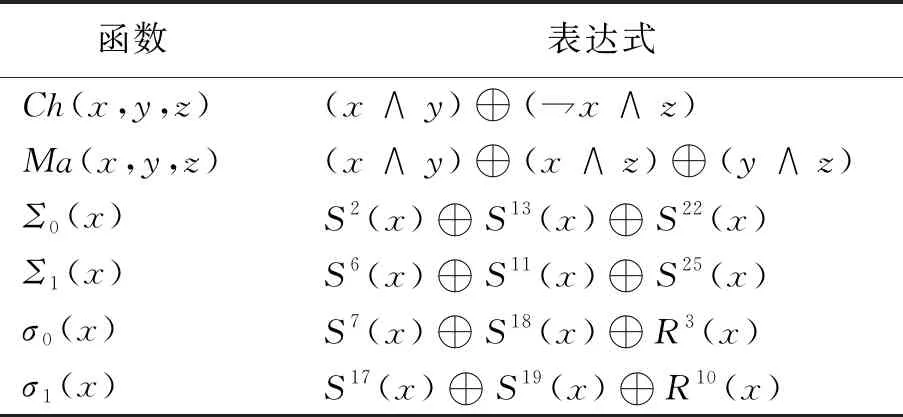
表2 SHA - 256算法中的逻辑运算
2 改进的SHA - 256算法
针对传统的SHA - 256算法无法满足区块链对大数据的快速处理,本文对传统的SHA - 256算法做如下改进:首先将SHA - 256算法按512位进行分组划分,并且将每一个分组再划分为8个64位子分组;其次对报文进行处理后,算法的输出由原来的8个32位分组变为4个64位分组;最后将上述4个64位分组级联生成一个256位的散列值.
改进的SHA - 256算法的执行过程如下:
第1步 在报文末尾处进行数据填充,填充后的报文长度对512取模后其余数为448.填充的方法是首先在原报文末尾处添加1个比特(用数字1表示),然后补充剩余的比特数(用数字0表示).
第2步 用64位比特数记录填充前的信息长度.
第3步 在改进的SHA - 256算法中装入标准的幻数,标准的幻数为:
A为0x36d219f41e0342b5,
B为0xf807493c33fac611,
C为0x1479c317abbfce09,
D为0x4dbabfa350149e5c.
第4步 对改进的SHA - 256算法进行4轮循环运算(每轮16个步骤),各轮所使用的线性函数如表3.

表3 每轮循环运算中的线性函数
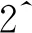
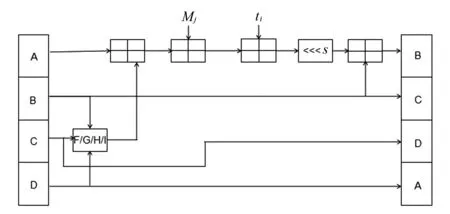
图3 改进的SHA - 256算法中的单次循环示意图

表4 名文字顺序
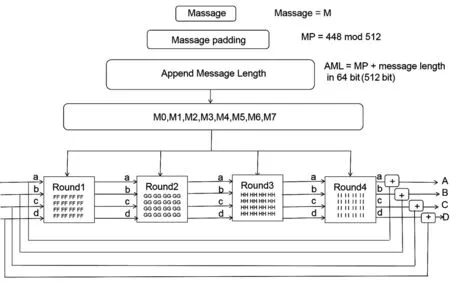
图4 改进的SHA - 256算法的运算流程
为了降低传统SHA - 256算法的复杂度,对上述改进的SHA - 256算法进行优化,即将算法中主循环的每轮16次迭代变为8次迭代,由此4轮迭代可共减少32次迭代.减少迭代次数(32次)后,明文字Mj的数量和顺序如表5所示.对比表4可知,算法减少32次迭代后,每轮所需要的明文字数量比之前减少了一半,由此表明减少迭代次数可有效提高算法的效率.
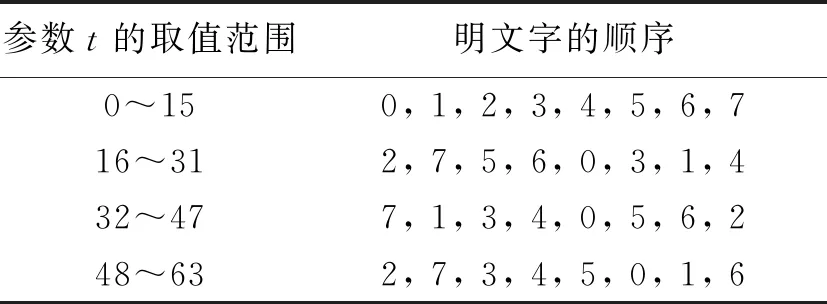
表5 名文字顺序
3 安全性分析
1)穷举攻击.本文采用天河二号超级计算机(计算速度为每秒3.39×1016次)对改进的SHA - 256算法进行抗穷举攻击验证.经计算知,采用天河二号超级计算机进行穷举攻击破解时平均需要运行1.22×1053a,由此说明改进的SHA - 256算法对抗穷举攻击具有良好的安全性.
2)生日攻击.由生日攻击原理可知,对改进后的SHA - 256算法进行生日攻击时大概需要尝试2128次哈希,若使用天河二号超级计算机对改进后的SHA - 256算法进行生日攻击破解时平均需要运行3.6×1014a,这说明改进后的SHA - 256算法对生日攻击具有良好的安全性.
3)差分攻击.由于改进的SHA - 256算法与传统的SHA - 256算法具有相同的迭代次数(64次),因此改进的SHA - 256算法也可以有效抵抗现有的差分攻击.
4)雪崩效应.选取100对报文进行雪崩效应实验.改进后的SHA - 256算法和传统的SHA - 256算法的雪崩效应实验结果见图5—图7.由图可以看出,改进的64次迭代的SHA - 256算法和改进的32次迭代的SHA - 256算法的坏点出现概率分别为3%和5%,而传统的SHA - 256算法的坏点出现概率为5%.这表明改进的64次迭代的SHA - 256算法的雪崩效果优于传统的SHA - 256算法.
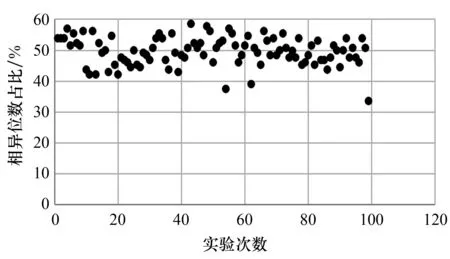
图5 改进后的SHA - 256(32 steps)算法的雪崩实验结果
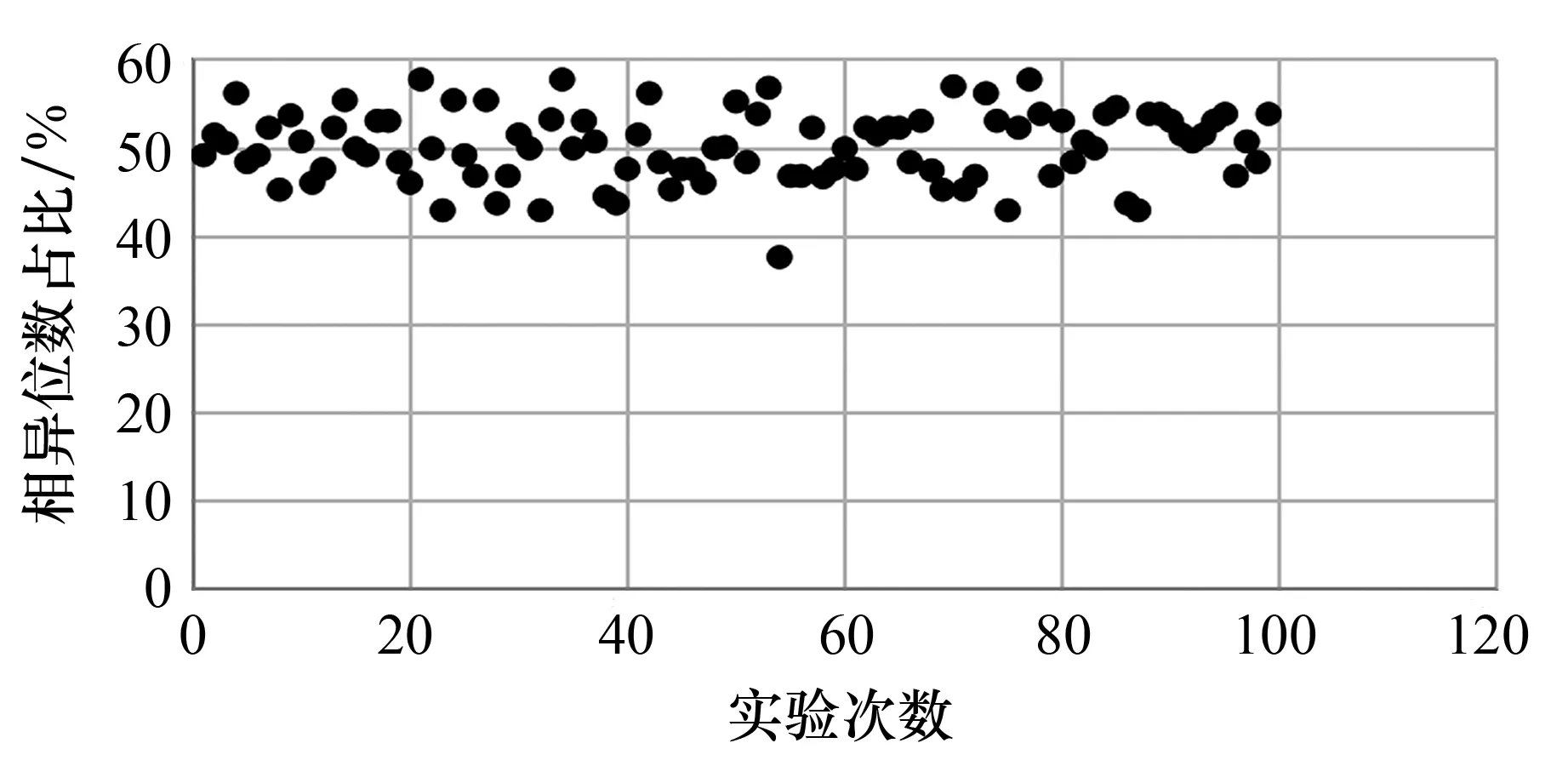
图6 改进后的SHA - 256(64 steps)算法的雪崩实验结果
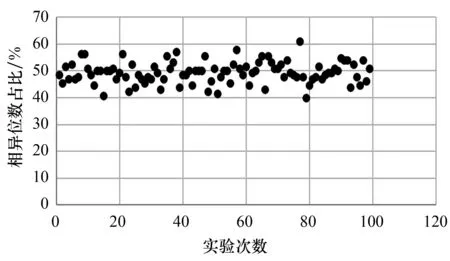
图7 传统的SHA - 256(64 steps)算法的雪崩实验结果
4 性能分析
为了验证方法的有效性,将改进的SHA - 256算法的处理速率分别与传统的SHA - 256算法和MD5算法的处理速率进行了比较.实验利用Python语言编程实现.计算机的配置为: Interl(R) Core(TM) i 5 - 5200U CPU@2.2 GHZ处理器, 64位win7操作系统.实验数据选取6个不同字节的数据,加密次数为10 000次.实验结果如图8—图10所示.由图可以看出,改进的64次迭代的SHA - 256算法和32次迭代的SHA - 256算法的计算效率比传统的SHA - 256算法平均分别提高了24%和140%, 改进的32次迭代的SHA - 256算法平均计算效率比MD5算法提高了32%.
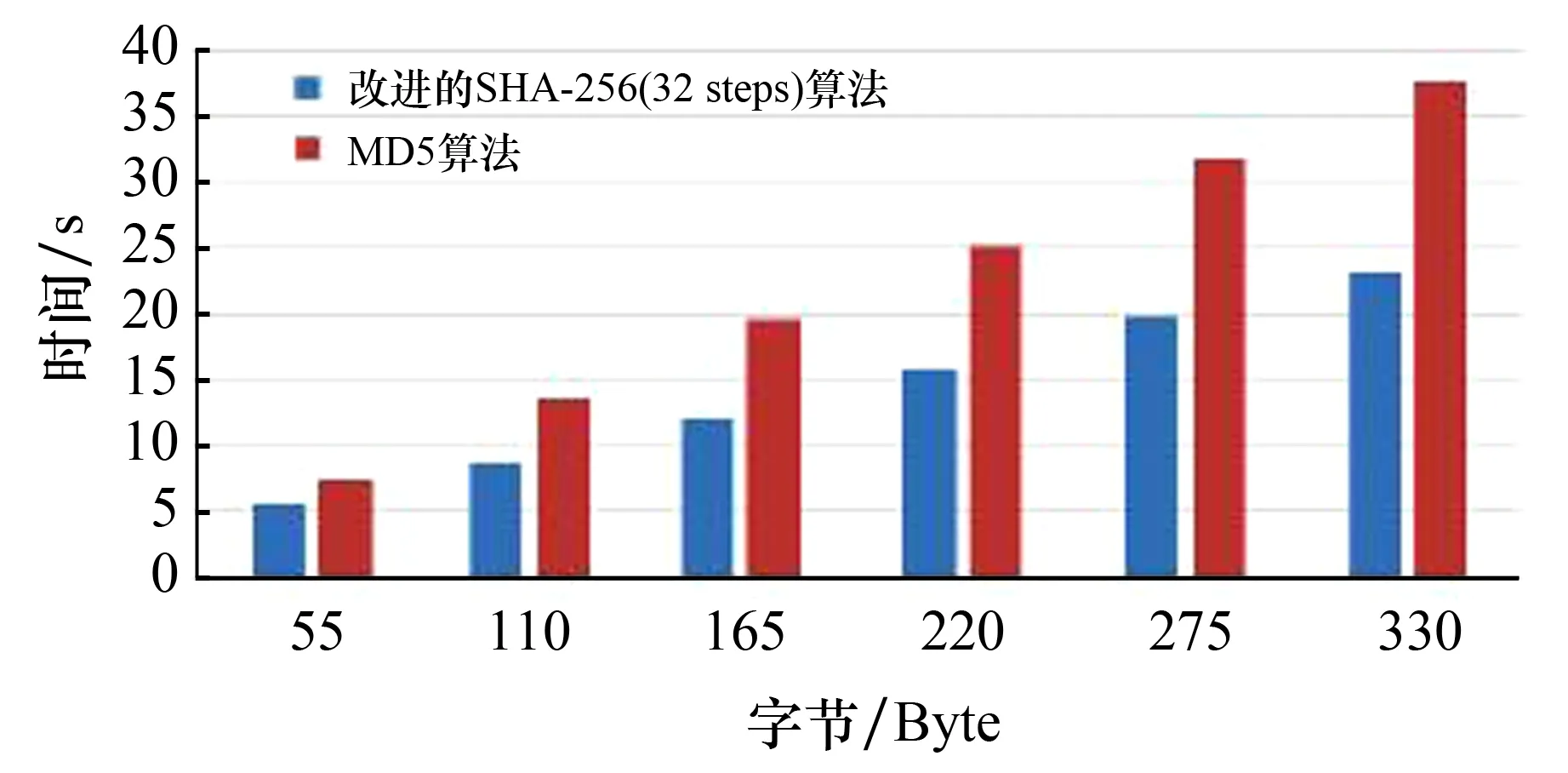
图8 改进的SHA - 256(32 steps)算法和MD5算法的处理速率
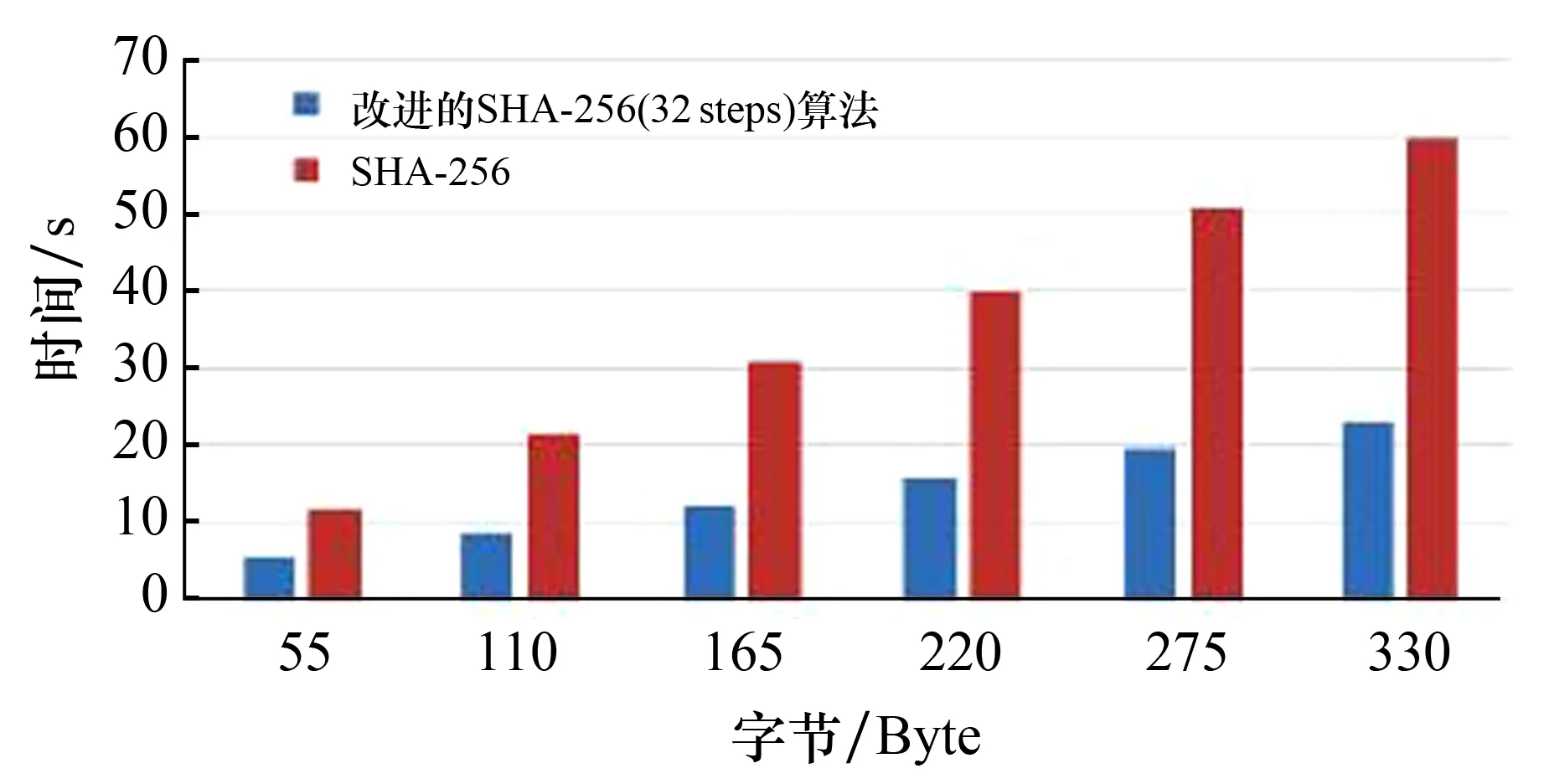
图9 改进的SHA - 256(32 steps)算法和传统的SHA - 256算法的处理速率
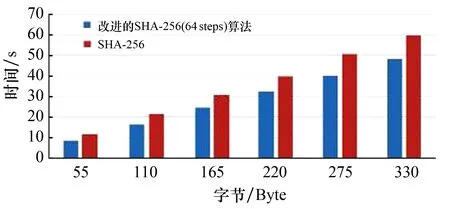
图10 改进的SHA - 256(64 steps)算法和传统的SHA - 256算法的处理速率
5 结论
研究表明,在保证算法安全性的基础上,本文改进的SHA - 256算法(64 steps和32 steps)的计算效率比传统的SHA - 256算法分别提高了24%和140%,改进的32 次迭代的SHA - 256算法的平均计算效率比MD5算法提高了32%,因此本文研究方法可为区块链技术提高数据处理效率提供参考.在今后的研究中,我们将在哈希函数中引入随机组合结构,以此进一步提高本文改进算法的安全性和适用性.

