三维空间向量积与旋度算子的高维推广

林开亮，吴艳霞

(1.西北农林科技大学 理学院，陕西 杨凌 712100；2.山东财经大学 数学与数量经济学院，济南 250014)

1 向量积

众所周知,在三维欧氏空间中,对两个向量v,w,除了数量积(也称内积或点乘)v·w,还有向量积(也称叉乘)v×w。而且,数量积的概念是高维欧氏空间的基础,在欧氏空间中度量长度、角度 (特别地,垂直关系)都依赖于数量积。那么,很自然地,我们可以问下述问题：向量积是否可以从三维空间推广到高维空间呢？对于这个问题,直到 1942 年才由Beno Eckamann(1917—2008)[1]考虑并完全解决。1983年,美国著名代数拓扑学家William S.Massey(1920—2017)从中提炼出以下代数定理:

(i) 〈v×w,v〉=〈v×w,w〉=0,

(ii) ‖v×w‖2=‖v‖2‖w‖2-〈v,w〉2。

正如Massey所指出的,定理1是著名的Hurwitz定理的推论。

定理2[3]当且仅当n∈{1,2,4,8}时，存在x1,…,xn与y1,…,yn的实系数双线性函数z1,…,zn使得

(x12,…,xn2)(y12,…,yn2)=(z12,…,zn2)

对一切实数值变量x1,…,xn与y1,…,yn都成立。

定理2又称为“1,2,4,8 定理”,它也可以用矩阵来表述,即

定理3[3]设B1,…,Bk是n阶实矩阵,且满足下述 Hurwitz 方程

(1)

定理2与定理3的证明可参见文献[3]。考虑到从定理2到定理1的推导有益于我们理解后面的论证 (从定理3推导定理4),这里我们给出定理1的证明。

xy=(a,v)(b,w)=(ab-〈v,w〉,aw+bv+v×w)。

‖xy‖2=‖ab-〈v,w〉,aw+bv+v×w‖2

=(ab-〈v,w〉)2+〈aw+bv+v×w,aw+bv+v×w〉

=(ab-〈v,w〉)2+a2‖w‖2+b2‖v‖2+‖v×w‖2+2ab〈v,w〉+

2a〈w,v×w〉+2b〈v,v×w〉

=a2b2+〈v,w〉2+a2‖w‖2+b2‖v‖2+‖v×w‖2

=a2b2+〈v,w〉2+a2‖w‖2+b2‖v‖2+‖v‖2‖w‖2-〈v,w〉2

=a2b2+a2‖w‖2+b2‖v‖2+‖v‖2‖w‖2

=(a2+‖v‖2)(b2+‖w‖2)

=‖x‖2+‖y‖2。

由定理2 知n+1∈{2,4,8},从而n∈{1,3,7}。

充分性的证明是构造性的,n=1的情况平凡,n=3的情况即我们熟知的向量积,n=7的情况可用八元数的乘法给出。[2]

定理1告诉我们,与数量积可定义于任意维数空间不同,满足适当条件的向量积仅存在于三维与七维空间。

2 旋度算子

在三维空间中,有与向量积密切相关的旋度算子。然而,在一般的高等微积分教材中,对高维空间并没有关于旋度算子的讨论。这就引出一个问题：是否与向量积的情况类似,关于旋度算子存在一个类似于定理1的结果？事实上,7年前有人在 Math.stackexchange 论坛上明确提出过这样的问题：“can the-curl-operator-be-generalized-to-non-3d?” 针对这一问题,我们得到下述平行于定理1的结论：

(i) 对任意的F∈Vn有

div(curlF)=0,

这里 div 是作用在Vn上的散度算子。

(ii) 对任意的f∈V,有

(iii) 对任意的F∈Vn有

证明 设满足条件 (i) (ii) (iii) 的旋度算子curl:Vn→Vn具有形式

根据条件(i),我们有

即

由于各个fl相互独立,所以对任意给定的l=1,2，…,n,有

在上式中令fl(x)=xixk,有

(2)

再看条件 (ii),对任意的f∈V,有

从而对每个i=1,2，…,n都有

在上式中令f(x)=xlxk有

(3)

现在考虑条件 (iii),为此我们先计算出

而

于是根据条件 (iii) 可知,对j=1,…,n有

注意到各个fl相互独立,所以有

令fl(x)=xkxr,则有

根据式 (3) 与 式(2) 有

从而上式可以改写为

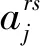
(4)

对每个j=1,2，…,n,构造n+1阶矩阵Bj:

(5)

下面验证,这n个矩阵B1,…,Bn满足Hurwitz矩阵方程 (1)。由于

从而

(6)

所以我们的目标是证明

(7)

容易算出

(8)

而根据式(4) 有

(9)

(8)(9)两式表明,要想证明式(7),我们只需验证

Aiej+Ajei=0。

(10)

由于上式对任意的r=1,2，…,n成立,所以Aiej+Ajei=0,即式(10) 成立。

应用定理3可推出n+1∈{2,4,8},从而n∈{1,3,7}。注意n=1时的旋度算子就是求导算子,而n=3时即得到经典的旋度算子,所对应的3个矩阵分别为

至于七维空间中的7个反对称矩阵,我们留给感兴趣的读者来构造。

3 与 Taussky-Stiefel 定理的关系

旋度算子与广义 Cauchy-Riemann 算子有密切的关系。

1939 年,Taussky 定义n维广义Cauchy-Riemann算子如下：设

L=(lij(∂))，

其中：lij(∂)是∂1,…,∂n的常系数线性组合,i,j=1,2，…,n，则矩阵L称为n维广义Cauchy-Riemann算子,如果存在矩阵

W=(wij(∂))，

例如,经典的 Cauchy-Riemann 算子是

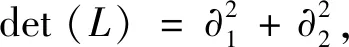
给出。

Taussky O的主要结果如下：

定理5[4]设n≥2,则n维广义Cauchy-Riemann 算子存在当且仅当n=2,4,8。

后来 Stiefel E[5]利用 Hurwitz 矩阵方程化简了 Taussky 的证明。因此定理5被称作Taussky-Stiefel定理。

事实上,定理 4 是定理 5 的推论。我们证明如下:

设有满足定理 4 条件的旋度算子 curl，现在构造作用于n+1维向量函数空间的一阶微分算子L,W如下:

因此根据定理5,我们有n+1=4或8,从而n=3或7。

4 小结与引申

前文我们证明了,仅在三、七维空间中存在向量积和旋度,我们又知道在三维空间,向量积与旋度之间有密切联系。于是我们提出这样的问题,定理1与定理4是否等价？或者它们可否统一？另一方面,我们关于定理1与定理4的证明都依赖于定理2或等价的定理3,它们表明2,4,8是极特殊的数。事实上,在数学中,有些数学对象仅当n=2，4，8时存在,实数域上的可除代数(仅有实数、复数、四元数和八元数)就是一个典型的例子,更多的例子来自拓扑,见文献[6]中 Ebbinghaus H D的文章。