倾斜气井临界携液流速预测新模型

王武杰，崔国民，魏耀奇，潘杰

（1.上海理工大学能源与动力工程学院，上海市动力工程多相流动与传热重点实验室，上海 200093；2.国家石油天然气管材工程技术研究中心，陕西宝鸡 721008；3.西安石油大学石油工程学院，西安 710065）

0 引言

准确预测临界携液流速对诊断气井积液状况、解决含水气井稳产问题、挖掘煤炭地下气化开发潜力至关重要[1-3]，同时，其对促进致密油气快速规模发展，早日实现中国“能源独立”战略具有积极意义[4-5]。越来越多的实验数据表明，倾斜气井的携液能力最差，预测也最为复杂和困难[6-7]。因此，有必要对倾斜气井临界携液流速的预测展开深入研究。分层流作为倾斜管道气液两相流动的主要流型被普遍认可。分层流流型下，井筒内气液两相的周向分布对流动特性有至关重要的影响，尤其对液相流量较小而气相流量较大的情形更甚[8-9]。目前对临界携液状态下的气液相分布缺乏量化研究，且尚无倾斜管道气液两相临界流动条件下的相界面摩擦因子计算模型。基于此，本文分别考察单位管长气液两相系统重力势能、表面自由能和气相动能的改变量，并根据能量最小原理确定临界携液状态下气液相分布的结构参数；同时采用实验数据修正相界面摩擦因子计算模型，使预测模型封闭；并将模型应用于倾斜气井临界携液流速的预测，以评估模型的应用效果。

1 实验系统

本文通过可视化实验，模拟气井携液的动态过程，实验装置如图1所示。

图1 实验装置图

分别采用水和甘油、水的混合溶液（二者体积分数均为 50%）模拟井下积液，利用空气模拟天然气。实验条件下空气密度ρa=1.184 kg/m3，空气动力黏度μa=1.849×10-5Pa·s；水密度ρw=997.05 kg/m3，水动力黏度μw=8.900 8×10-4Pa·s；水、甘油混合溶液密度ρgw=1 139.56 kg/m3，水、甘油混合溶液动力黏度μgw=6.882×10-3Pa·s；空气、水表面张力σaw=0.071 97 N/m，空气与水、甘油混合溶液表面张力σagw=0.067 11 N/m。

分别选用外径50 mm、壁厚5 mm和外径70 mm、壁厚5 mm的有机玻璃管进行实验，步骤为：①在管内低洼处注入一定体积的液体，通过风机增压向玻璃管内注入压缩空气，计量压力和流量；②采用变频器实现气体流速的连续可调，直至低洼处的积液完全铺展于上倾段并与管壁相对静止（此时达临界气体流速）。

2 模型建立与求解方法

2.1 受力分析与控制方程

临界气体流速条件下，倾斜管内流型为波状分层流，液膜在重力、相界面和壁面切应力的作用下处于平衡状态。此时，近气相侧的液膜在相界面切应力的作用下向下游运动，而近壁面侧的液膜在重力作用下回流，即液膜内部存在循环流动。倾斜井筒微元段内液膜受力如图2所示。上述流动过程可简化为稳态一维流动，并忽略加速压降，可对气、液相分别建立动量方程：

图2 倾斜井筒内液膜流动与受力分析

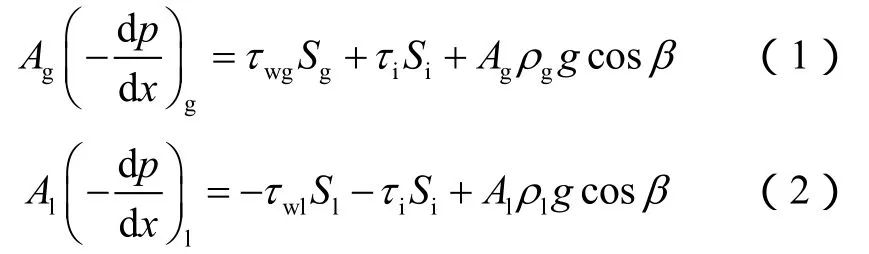
流动过程中近似认为气相与液相的平均压力梯度相等，联立（1）式和（2）式可得控制方程：

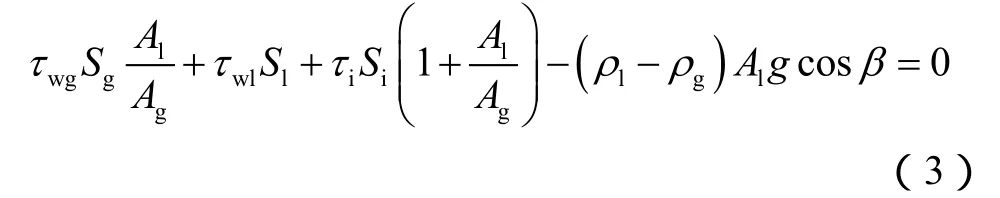
上式中，几何参数与气液相分布有关，应力参数与持液率、各相速度和摩擦因子有关。通过闭合几何参数和应力参数可使控制方程闭合。

2.2 气液相分布

根据Brauner等[10]的研究，液膜的周向分布如图3所示。其中，O和O1分别表示井筒流道的截面轴心和虚拟圆圆心。控制方程中的几何参数采用下式计算：

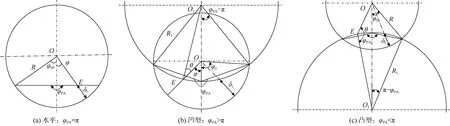
图3 井筒周向的液膜分布

不同相界面假设下的几何参数的计算式见表1。

表1 不同相界面下的几何参数计算关系式

2.3 能量最小原理

在相界面形状由水平变为弯曲的过程中，重力、切应力和表面张力将引起系统势能、动能和表面自由能的变化。临界条件下，单位管长气液两相系统总能的改变量可表示为：

基于能量最小原理，单位管长系统总能量最小时，相界面结构最稳定，即：

①单位管长重力势能的改变量[10]

②单位管长表面自由能的改变量

③单位管长气相动能改变量

根据七分之一次方定律，圆管内湍流气相的速度分布表示如下：

单位管长气相动能改变量采用下式计算：

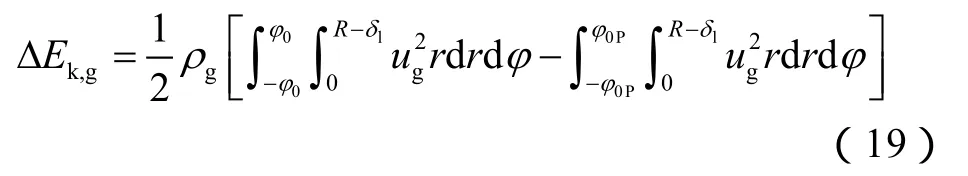
2.4 剪切应力计算

Taitel等[11]给出了相关应力计算表达式：

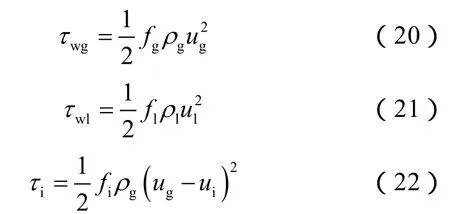
Banafi等[12]实验研究指出 Taitel模型可准确预测气液两相低持液率流动条件下的气壁面摩擦因子，表达式如下：

层流时，Cg=16，m=1；湍流时，Cg=0.046，m=0.2。

Biberg[13]指出，倾斜管道光滑分层流条件下，平均液壁面切应力与平均相界面切应力满足下式：

上式中f（φ0P）是 难以获得解 析 解 的积分项。Biberg[13]给出以下近似计算关系式：

式中，an和bn的取值见表 2[13]。该近似值的最大绝对误差不超过2×10-6。

表2 近似关系式（（26）式）中参数an和bn的取值

准确计算相界面摩擦因子是预测相界面切应力的关键。倾斜管道中，界面波和持液率对相界面摩擦因子的影响较大。界面波动特性主要取决于机械能从气相向液相的传递速率以及液体中黏性耗散速率，而这一过程受倾角的影响[14]。随着管道倾角的增加，重力对界面波生长的约束减弱，使得倾斜管中的液层表面更易于观察到界面波。本文认为在倾斜管道中，重力对倾斜管内临界状态下的界面波动作用更加显著。因此，一方面将界面波等效为管壁的相对粗糙度，另一方面，引入倾角对相界面摩擦因子进行修正[14]，具体过程如下：

其中，无因次相界面湿周定义为：

再考虑倾角的影响对其进行修正：

式中，A和B与流体物性和管道条件有关[15]。

2.5 模型求解方法

控制方程（（3）式）可以视为持液率的函数，即：f（ε）=0。零始终是方程f（ε）=0的一个解。的函数图像如图4所示。当usg=usg,cr时，f（ε）=0只有一个非零解，且该非零解在（0，0.1）区间求得，求解步骤如图5所示。

图 4 函数 f（ε） 1/3在不同流动条件下的变化曲线

图5 模型求解过程示意图

3 结果分析与实例验证

3.1 气液相分布预测结果与分析

对控制方程无因次化处理后可得：

其中

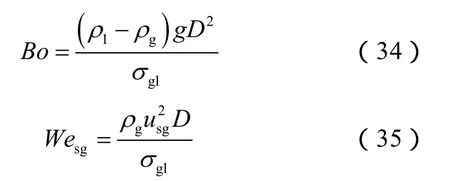
由上式可知，临界状态下的气液相分布与邦德数、气相表观韦伯数、持液率和井斜角有关。基于能量最小原理，量化气液两相系统总能量随相界面结构的变化，并以空气和水为例，分别考察上述 4个因素对管内气液相分布的影响，计算结果见图6（图中红色数据点为各工况下的能量最小值点）。可以看到：①随着管径的增加，最稳定的气液相分布（对应能量最小值）所对应的相界面弯曲角从125°（微凸）逐渐趋于180°（水平）；反之，管径越小，在润湿性和表面张力的影响下相界面弯曲角越小，呈现凸型结构的液相分布（见图6a）；②随着井斜角的增加，重力抵消润湿性和表面张力的作用效果更加显著，使最稳定的气液相分布所对应的相界面弯曲角从120°（微凸）趋近于180°（水平）（见图 6b）；③结合图 6c、图 6d可知，气体流速和气相密度增加，使气相动能也增加，在润湿性和表面张力的影响下相界面弯曲角减小（变凸）有利于降低系统表面自由能；④随着持液率的增加，液相重力势能的影响增大，有利于稳定原来水平相界面的形状，同时界面微凸也可减小持液率增加导致的系统表面自由能的增加。但是在液相密度远大于气相密度的低压系统下，液相重力势能起主导作用（见图6e），随着持液率的增加，最稳定的气液相分布所对应的相界面弯曲角从105°逐渐趋于165°（近水平）。综上所述，低持液率流动条件下，受表面张力和润湿性的影响，相界面呈现微凸，符合如图7所示的实验观察结果。

图6 液相分布的模型预测结果

图7 实验观察的临界状态下的气液相分布示意图

3.2 实验结果与分析

图 8为临界携液气体流速和临界压力梯度的实验结果。由图可知，临界携液流速和临界压力梯度随着倾角的增加呈非线性增加。在相同的管道倾角下，液相密度或者黏度越大，临界携液流速越大。这与Birvalski等[16]的实验结果一致。同时，管径增加使临界携液气体流速增加。这是因为在相同持液率下，界面形状的变化不及Bo和Wesg数对临界携液流速的影响显著，要使控制方程依然成立，必须提高气体流速，以抵消管径增加引起的Bo/Wesg的增量。

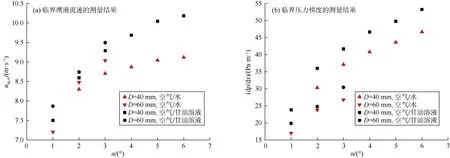
图8 临界携液流速和临界压力梯度的实验结果

3.3 倾斜管内相界面摩擦因子计算模型

采用Birvalski等[16]和本文的实验数据，基于简化后的水平相界面形状封闭几何参数，对不同倾角下的相界面摩擦因子修正参数进行反算，并通过数据拟合得到相界面摩擦因子修正参数（f（α）），计算结果如表3所示。采用表 3中相界面摩擦因子修正参数对相界面摩擦因子计算公式（（31）式）进行修正后，模型的预测值达到了非常高的精度。皮尔逊相关系数相对较高。

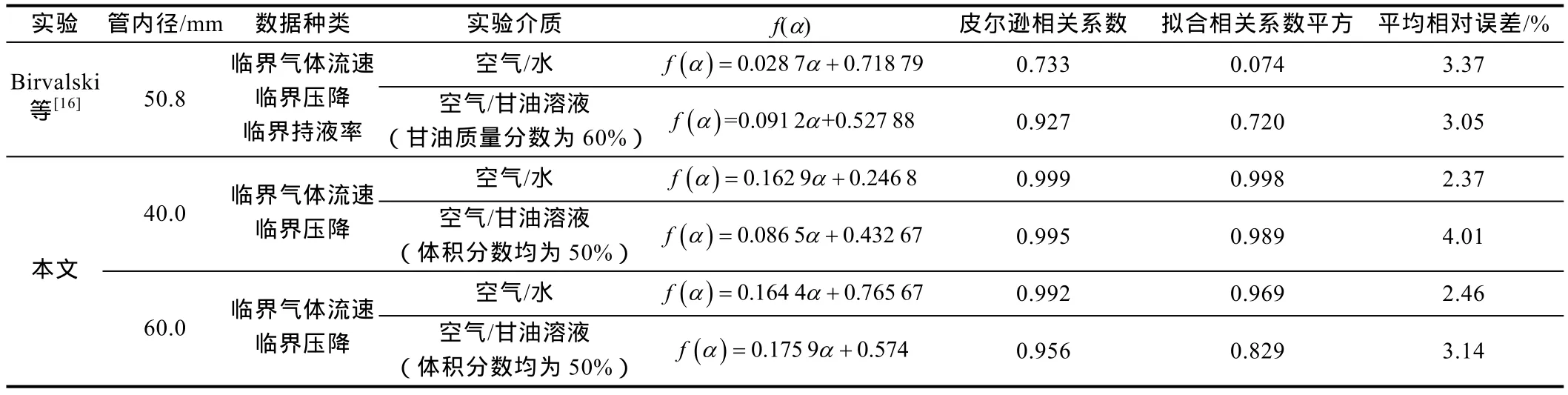
表3 不同实验条件下的相界面摩擦因子修正参数

由表3可知，f（α）的斜率为正值，即表明相界面摩擦因子随着倾角的增大整体呈现递增的趋势。主要是因为倾角的增加使得约束界面波动的重力分量减小，导致界面波动更加剧烈和明显。同时，f（α）小于1，表明在微倾管道内低持液率流动条件下，相界面摩擦因子要小于相同气体流速下水平管道相界面摩擦因子预测值，主要原因是当管道接近水平时，倾角对界面波的影响不如持液率的影响显著。本文基于实验数据，结合无因次化分析，给出相界面摩擦因子修正参数的计算式：

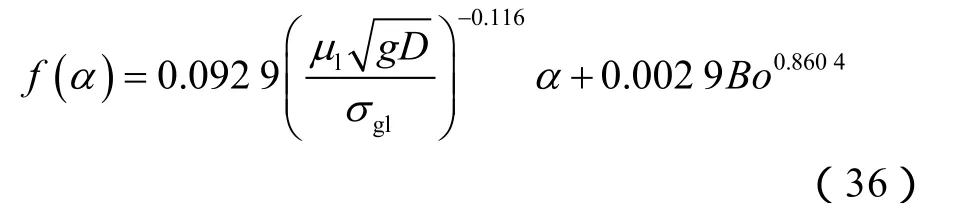
3.4 模型对比与工程实例验证

将模型预测结果与实验数据进行对比（见图9）。本文模型预测的临界携液流速随管径的增加而增加，随液相密度和黏度的增加而增加（同管径下，甘油溶液的临界携液流速大于水的临界携液流速），这一规律与符合 Birvalski等[16]和 Rastogi等[17]的实验结果；临界压力梯度的预测结果随管径的增加而减小，符合实验结果，管径的增加使液相水力直径增加是压力梯度减小的重要原因。对比本文实验数据，新模型预测临界携液流速和临界压力梯度的平均相对误差分别为1.19%和3.02%。同时，临界携液流速随倾角的增加先增大后减小，最大临界携液流速对应的管道倾角随管径的增加而增加，同时也受流动介质物性的影响。本文模型模拟计算发现，标况下天然气携矿化水时，最大临界携液流速对应的管道倾角分别为 30°（D=50.67 mm）、37°（D=62.00 mm）、40°（D=75.9 mm）和 45°（D=100.53 mm）。

图9 本文模型预测结果与实验结果对比

本文模型应用于高压系统时需要对预测结果进行转换。本文从能量角度出发，认为高、低压管道系统内，临界条件下单位体积气液两相间传递的机械能应相等，即：

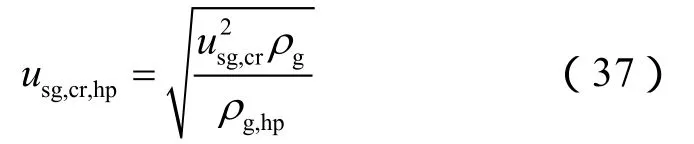
为便于比较，将临界携液流速转换为标况下的临界携液流量：

当天然气的实际流速大于倾斜气井中临界携液流速最大值时，气井才能连续携液。气田现场需结合方位测井资料来确定倾斜气井的最大临界携液流速。选取中国普光气田和延长气田42口气井的生产数据，并与实际产气量绘制交会图（见图10），可以看到本文模型仅误判1口气井，误判率2.38%，说明本文模型的预测结果具有较高的可信度，可对倾斜气井积液进行有效判断。

图10 本文模型预测结果与对比

4 结论

低持液率流动条件下，相界面形状更容易受到壁面润湿性和表面张力的影响呈现弯曲，管径越小、持液率越小、井斜角越小、气体流速越大、气相密度越大时，相界面弯曲越明显。

气井临界携液流速随井斜角的增加呈现非线性先增后减的趋势；最大临界携液流速对应的井斜角随井筒直径的增加而增大，同时也受气液两相物性的影响。

本文模型预测临界携液流速与临界压力梯度的平均相对误差分别为1.19%和3.02%，现场倾斜气井积液误判率2.38%，可对倾斜气井积液进行有效判断。

符号注释：

an，bn，A，B——常系数，无因次；AT——油管截面面积，m2；Ag——气相流动通道面积，m2；ΔAgl——单位管长气液相接触面面积的变化，m2/m；Al——液相流动通道面积，m2；ΔAlw——单位管长液壁接触面面积的变化，m2/m；Bo——邦德数，无因次；Cg，m——与流态有关的系数，无因次；D——油管内径，m；DH,g——气相水力直径，m；Dl（φ0P）——不同液相分布角下的等效层流直径，m；fg——气相摩擦因子，无因次；fi——相界面摩擦因子，无因次；fl——液相摩擦因子，无因次；f（α）——相界面摩擦因子修正参数，无因次；f（φ0P）——与液相分布角有关的函数，无因次；F——中间变量，无因次；g——重力加速度，m/s2；k——相界面绝对粗糙度，m；n——常系数编号；p——压力，Pa；Qcr——临界携液流量，m3/d；r——距离井筒轴心的径向位置，m；R——油管半径，m；Reg——气相雷诺数，无因次；R1——虚拟圆半径，m；Sg——气相湿周，m；Si——相界面湿周，m；si——无因次相界面湿周，无因次；Sl——液相湿周，m；T——热力学温度，K；ug——气相真实流速，m/s；g——平均气相真实速度，m/s；ug,max——最大气相真实速度，m/s；ui——相界面真实流速，m/s；ul——液相真实流速，m/s；usg——气相表观流速，m/s；Δusg——气相表观流速迭代步长，m/s；usg,cr——临界携液气相表观流速，m/s；usg,cr,hp——高压系统下的临界携液气相表观流速，m/s；Wesg——气相表观韦伯数；x——流动方向坐标，m；YGPC——弯曲相界面的重心位置，m；YGP——水平相界面的重心位置，m；Z——压缩因子；α——管道倾角，（°）；β——井斜角，（°）；ΔEk,g——单位管长气相的动量改变量，J/m；ΔEp——单位管长气液两相系统的重力势能改变量，J/m；ΔEs——单位管长气液两相系统的表面自由能改变量，J/m；ΔEtot——单位管长气液两相系统的总能量改变量，J/m；δl——液膜厚度，m；δl（φ）——液膜厚度分布，m；ε——持液率；ε0——持液率迭代初值；Δε——持液率迭代步长；θ——润湿角，rad；μa——空气动力黏度，Pa·s；μg——气相动力黏度，Pa·s；μgw——水、甘油混合溶液动力黏度，Pa·s；μl——液相动力黏度，Pa·s；μw——水动力黏度，Pa·s；ρa——空气密度，kg/m3；ρg——气相密度，kg/m3；ρg,hp——高压系统下的气相密度，kg/m3；ρgw——水、甘油混合溶液密度，kg/m3；ρl——液相密度，kg/m3；ρw——水密度，kg/m3；σaw——空气、水界面的表面张力，N/m；σagw——空气与水、甘油混合溶液的表面张力，N/m；σgl——气液界面的表面张力，N/m；τi——相界面剪切应力，Pa；——平均相界面切应力，Pa；τig——相界面反作用于气相的相界面切应力，Pa；τgi——气相作用于相界面的相界面切应力，Pa；τwg——气壁面剪切应力，Pa；τwl——液壁面剪切应力，Pa；τwl——平均液壁面切应力，Pa；φ——任意液相分布角，rad；φ0——弯曲相界面的液相分布角，rad；φ0P——水平相界面的液相分布角，rad；φPA——相界面弯曲角，rad。下标：g—气相；l—液相。