数据驱动的异常检测与预警问题

李颖莹 郭亦可 蔡艺茗

华北水利水电大学 河南 郑州 450045

1 研究背景

推动生产企业高质量发展,最根本的底线是保证安全、防范风险,而生产过程中产生的数据能够实时反映潜在的风险。在工厂一天的生产中,各物理量不可能保持恒定不变,其观测数值必将产生波动,这可能是电机设备的功率浮动、车间气温变化亦或是供电电压产生跌落导致的,也可能是传感器自身精度所致。温度、浓度、压力等与安全密切相关的数据的波动十分重要,对其数据波动的判定和预测值得深入研究。

2 数学模型假设

假设1:数据库内的所有数据都是真实有效的;

假设2:假设某一类事件出现频率较多时,该事件的某个属性对应的参数分布概率可用同类事件中该参数出现的频率近似表示;

假设3:忽略主成分分析中次要成分带来的微小影响;假设4:假设传感器的精度保持不变

3 数据预处理

考虑到数据库的数据庞大,首先对数据进行归一化预处理,将这些数据转为[0,1]之间的数,可以消除数据因大小不一而造成的偏差。数据的归一化有很多方法,本文采用最大最小法对传感器的数据进行归一化处理。数据进行归一化的公式如下所示:

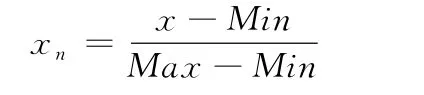
4 模型的建立与求解

4.1 对数据进行主成分分析

考虑到数据集中传感器有100组数据,过多的数据量对分析造成了影响,故选用主成分分析法进行分析,并对指标进行聚类。现有由100个样本作为行（行数为n）,5519个指标作为列（列数为p）而组成的551900个元素的样本矩阵x（由于该矩阵过于庞大,故略去出变化过程中的矩阵,以范式代表它的变化）:

本文选取累积贡献率达到百分之八十的主成分,其中前36个主成分的累计贡献率为80.61%,故将100个指标降为36个指标进行分析。

4.2 ARIMA时间序列分析

ARIMA模型是时间序列分析的典型模型,是一种分析时间序列的最为发达和广泛应用的方法。ARIMA模型,也叫Box-Jenkins模型,能够扩展成分析时间序列,包括周期性趋势。基于关于时间序列的特征的先前研究,可以指定时间序列,即自回归顺序（p）、差分次数（d）和移动平均顺序（q）三个参数来分析。ARIMA模型表示与时间组有关的随机变量与相应的数学模型之间的关系,以便根据过去的时间序列和目前的数 值预测该序列的持续发展及其未来的数值。ARIMA模型主要通过以下4个步骤进行建模:序列平稳化处理、模型阶数判定、参数估计、模型监测应用。

由于数据的波动较为频繁,不利于寻找规律,故对序列进行滤波处理,将波动较小的部分去除,将主成分分析完成后的36个主成分滤波前后的数据做可视化处理,如下图所示（篇幅有限,仅展示部分）:

图4-1 滤波波动图

首先观察蓝色曲线,滤波滤除的即是短暂且较小的波动,这类波动是独立且随机的,因此可以认为是传感器误报,将其视为非风险性异常。进行滤波后,观察红色曲线,可以看到主成分三、四等的红色曲线没有较大的波动,且具有一定的周期性,很有可能是自动化生产线器械的自然规律,如异步电机的调速等,因此亦判定为非风险性异常。而主成分一、二、五等具有明显的持续性和联动性,其波动表现在时间序号1931等处呈集中爆发样式,且在此之后并未快速回复,因此将它们判定为风险性异常数据。

综上所述,小组使用主成分分析法和ARIMA时间序列模型,提出了风险性异常数据的判定方法,使问题一得到解决。

4.3 引入临近分析法

为了按照真实的比重给各个波动的主成分,需要使用临近分析法对主成分进行加权,NCA是一种基于邻域分量的特征选择方法,在有监督的机器学习方法中,通过NCA多步跌代算法对用于分类的特征向量进行分析,以此获得不同的特征向量的分类中的权重大小,可根据权重的大小对原始的特征向量进行进一步筛选,进一步对数据进行降维,对整个训练网络进行优化。在第一问中我们已经通过PCA降维算法对传感器数据进行了排序和权重计算,在本问中进一步利用NCA对影响恐怖袭击等级的特征向量的排序和权重进行进一步的讨论,以此来得出风险性异常数据异常程度的量化评价方法。

计算得出的NCA与PCA特征向量权重/得分如下图所示:

图4-2 NCA特征向量得分示意图

由此,小组对每一时刻的主成分均进行了加权后计算数值结果,并将其线性映射到（0,100）的区间内,并挑选出结果最高的五个时刻并记录。部分异常传感器的波动图像如下图所示:

图4-3 部分异常传感器的波动图

4.4 数据拟合与灰色预测模型

为了建立预测模型对未来（23:00-24:00）进行预测,分别采用数据拟合和灰色预测模型进行建模。数据拟合采用Matlab数据拟合工具箱进行,通过尝试不同的拟合函数。采用机器学习的算法进行网络训练,其一般的网络如图7.1所示。其中恐怖等级特征向量作为网络的输入,等级标签作为网络的输出,输入信号从输入层经隐含层逐层处理,直至输出层,每一层神经元只影响下一层神经元状态。如果输出得不到期望输出,则转入反向传播。

步骤1:网络初始化。根据系统输入输出序列（X,Y）确定网络输入层节点n、

隐含层节点数I,输出层节点数m,初始化输入层、隐含层和输出层神经元之间的连接权值Wij,Wjk。初始化隐含层阈值a,输出层阈值b,给定学习速率和神经元激励函数。

步骤2:隐含层输出计算。根据输入变量X,输入层和隐含层连接权值ijw以及隐含层阈值a,计算隐含层输出H。

式中,l为隐含层节点数;f为隐含层激励函数,该函数有多种表达形式,其中默认的激励函数为:

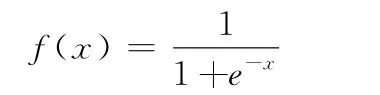
步骤3:输出层计算。根据隐含层输出H,连接权值Wjk和阈值b,计算BP神经网络预测OK。

步骤4:误差计算。根据网络预测输出O和期望输出Y,计算预测误差。

步骤5:权值更新。根据网络预测误差e更新网络连接权值Wij,Wjk。

步骤6:判断算法迭代是否结束,若没有结束,返回步骤2。

可以看到训练后的模型预测值与训练集数据已经十分接近,故将训练后的参数代入到ARIMA时间序列预测模型中。

4.5 安全评价系统的建立

在第三问中已经预测了23:00-24:00的数据,小组已经掌握了全面的时间序列分析,则由一二问的数学模型可以得到任意时间点的异常程度得分,由于异常程度与安全性是相反的逻辑关系,故异常程度得分取线性负相关后映射到（0,1）内,并以30分钟为域进行积分,将积分后得到的结果映射到（0,100）内。

4.6 灵敏度分析

敏感性分析一般借助simlab软件,首先通过simlab软件进行样本采样,生成.SAM文件（我定义了7个参数）,然后读取文件中的参数值,代入PROSAIL模型得到的结果生成是simlab可以读取的模型结果文件,得到敏感性分析如下图所示:

图4-4 敏感性分析效果图

由此可见,本模型的敏感性程度适中,不存在明显问题。

5 结束语

5.1 模型评价

本模型的优点是使用主成分分析法降低了数据的维度,使得算法的空间复杂度大大降低,同时使用ARIMA时间序列模型进行波动异常值筛选,经检验有较高的准确性。同时,为了准确预测23:00-24:00的未来走势,使用机器学习来对ARIMA模型的参数进行优化,得到了精准的预测,并对敏感性进行了检验。

5.2 模型改进

在算力足够的情况下,应该继续扩大主成分的权值到95%左右,这样得到的结果将更为精确;同时,对波动的滤波可以分段分层进行,以保证将所有异常值全部找到,目前使用的滤波方法的阈值选择过于主观,并未客观分析异常波动与波动幅值之间的关联性。