基于向导点法反演水文地质参数

何金沙，李春光，，吕岁菊，杨佩瑶，黄传霁

（1.宁夏大学土木与水利工程学院，银川750021；2.北方民族大学数值计算与工程应用研究所，银川750021）

0 引 言

水文地质参数在地下水资源评价、数值模拟、开发利用等方面具有十分重要的作用。地下水数值模型所能承载的某一种参数的最大维度等于该模型的网格剖分数目，大多数情况下观测数据包含的信息有限，直接对所有网格的参数进行反演具有一定的难度。而参数化方法通过某种特定数学关系简化实际参数组，无需对数值模型单个网格进行参数估计，仅反演简化后的参数组，再对已估参数点进行插值，从而得到含水层参数的估计场。传统的地下水参数分区人为的将模型区域划分为若干个小分区，每个分区用一个参数表示，在参数估计过程中只反演这些分区的参数的值[1]。然而这种区域的划分往往带有一定的主观性，不能很好地反映真实参数场的空间结构。

近年来，随着数值模拟技术的发展，向导点法成为求解非均质水文地质参数的一种新途径。向导点法通过在模型区域中布设一定数量的点，估计这些点处的参数值并进行插值以获得整个参数场的估计场。该方法与地统计学的结合可有效克服传统分区的缺点[2]，获得的参数场更符合真实情况[3]。在先验信息（如地质资料）丰富的情况下，可以依据当地的地质情况布置观测井与向导点，获得更加精确的水文地质参数场。例如Young S[4]基于Edwards-Trinity 高原和Pecos 峡谷的地质资料，通过在不同研究区域内均匀布置向导点，求解了水文地质参数。在缺乏先验信息的情况下，以往的研究都是将向导点与观测井均匀布置在整个研究区域。例如姜蓓蕾[5]使用该种布置方式，讨论了向导点个数对反演结果的影响。这种布置方式虽然被广泛采用，但是学者们并未对其展开深入研究，主要原因是向导点的数量关系可以定量描述，但观测井与向导点位置描述起来不是十分方便。本文采用观测井与向导点分布范围占研究区面积的比例来描述两者的位置关系，该方法可以不受区域面积和形状影响，不仅对于规则研究区域有效，还可以运用到不规则的研究区域。在此基础上，通过理想算例研究了观测井与向导点不同分布范围以及渗透系数场初值对反演结果的影响，为向导点法在水文地质参数反演中的推广提供了依据。

1 计算程序与算法

1.1 向导点法

向导点法起源于地质统计学，通过在模型区域内布设一定数目的点(向导点)，反演这些点处的参数值，再经过克里金插值得到整个参数场的估计场[6]。向导点法反演参数场的主要步骤见图1，其中Modflow 程序调用次数表示地下水模型Modflow.exe 运行次数，优化迭代次数等于PEST 程序循环次数。向导点法用于解决高维不适定问题，即向导点个数要大于观测井个数[7]。在先验信息不足的情况下，向导点应均匀分布在研究区内。此外，在参数估计中不同位置的观测井对目标函数的贡献不同，观测井应尽可能的包含更多的含水层信息。如果初始参数向量与最优参数向量相差较大，参数估计问题陷入局部最优，难以找到目标函数的全局最优解。

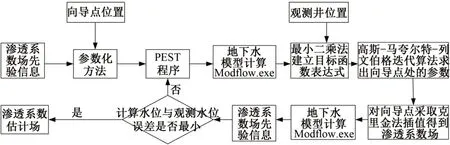
图1 向导点法反演参数场的主要步骤流程图Fig.1 Flow chart of the main steps of inversion of parameter field by the pilot point method

1.2 Gauss-Marquardt-Levenberg 迭代算法

大多数情况下，模型参数与观测值之间的关系都是非线性的，在求解过程中必须将非线性模型线性化。本文主要研究渗透系数与观测水位之间的关系，假设二者之间的非线性关系用函数c=M(b)表示，该函数可看作是n维参数空间映射到m维观测空间[函数c=M(b)所有待估模型参数的导数必须连续可导]。某一初始渗透系数向量b0对应的模型观测水位向量为c0，即：

任意向量b与其对应向量c的关系，可用如下泰勒展开式表示：

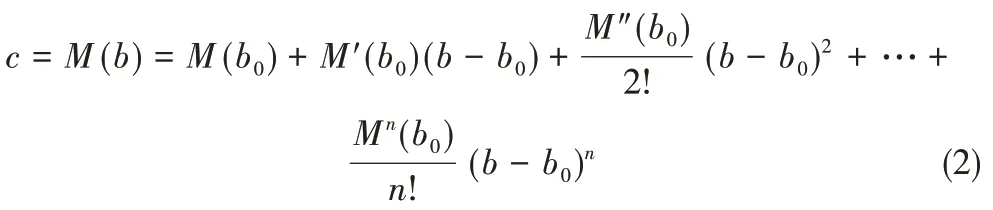
当b-b0足够小时，可以忽略式(2)中二阶以上的高阶项，从而简化为：

其中矩阵J是函数c=M(b)在b0处的雅克比矩阵(Jacobian Ma⁃trix)，共有m行n列，每行的元素为对应的待估模型参数的偏导数。

目标函数是模型计算水位与实际水位之差的平方和，而参数估计过程实际上是最小化目标函数的过程。假设n阶对角矩阵Q的第Z个对角元素表示的是第i个实际观测值的权重W的平方，cr表示实测水位向量，则非线性模型参数反演问题的目标函数表示为：

目标函数需要反复迭代更新雅可比矩阵J与参数向量b以使b-b0到达最小，定义参数更新向量b-b0为u，则u可表示为：

假定残差向量r=cr-c0，则式(5)可写为：

若目标函数Φ的梯度为g，则向量

在公式(6)中加入Marquardt参数，使估计初期参数更新向量u靠近向量g的反方向，u的表达式变为：

式中：α为Marquardt 参数；I为n阶单位矩阵；梯度向量g又可定义为g=-2JTQr。

高斯-列文伯格-马夸尔特迭代算法是在高斯—牛顿迭代法的基础上进行改进而来的，用于求解广义非线性加权最小二乘最小化问题[8]。该方法在每次迭代过程中，通过对待估模型参数进行求导将非线性模型线性化，同时更新参数向量，计算新的目标函数，不断重复迭代优化过程，直到目标函数满足要求。

1.3 PEST程序

PEST( 全称Parameter Estimate) 是由澳大利亚Water Numerical Computing 咨询公司开发的用于参数估计与不确定性分析的程序。PEST 程序第一个版本诞生于1994年，最初只具有非线性参数估计功能，经过20 多年的发展，目前已经具备了强大的正则化功能与不确定性分析功能。PEST 程序使用高斯-列文伯格-马夸尔特非线性参数估计方法，相比于其他非线性参数估计方法，该法可以在有效估计参数的同时节省大量运行模型的次数。最新版本的PEST 程序支持向导点法并且带有专门针对地下水问题的程序集，因此可以很方便地与Modflow等地下水模型进行藕合使用。

参数估计的目的是找到一个渗透系数向量，即渗透系数估计场，使得模型计算水位最大限度地拟合实际观测水位。为准确评估先验信息精度与反演精度，采用RMSE（Root Mean Square Error，均方根误差）作为衡量初始渗透系数场和渗透系数估计场（与实际渗透系数场）精度的评判标准，公式如下：

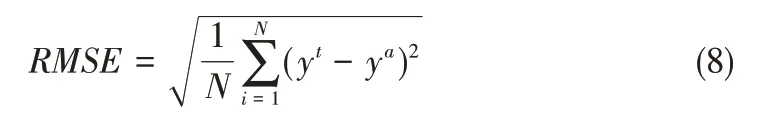
式中：n为参数个数；yt和ya分别表示参数的真实值和模型计算值；RMSE的值越小反演精度越高。

2 理想算例

本文采用确定性地下水数值模拟软件Visual Modflow[9]建立了一个二维承压含水层数值模型，如图2所示。假定该模型中含水层水平等厚，平面是边长为1000m 的正方形，底板高程为0 m，顶板高程为5 m，北边界为定水头边界，其余边界为隔水边界，上部接受0.000 5 m/d 的面状补给，模拟计算时间为365 d。通过克里金指数变异函数插值出地下水渗透系数对数场，作为实际渗透系数场（注：高斯变异函数在PEST 程序中运行结果会超出向导点值设定上下限，不建议使用[10,11]）。在研究区布置36 口井，作为地下水水位观测井。由于向导点法中参数反演属于不适定问题，向导点数要大于观测井数，因此在研究区内布置了64个向导点。

图2 理想算例中真实渗透系数场(log K)Fig.2 The real permeability coefficient field in the ideal case(log K)

在实际渗透系数场中选择16 个点，这些点的渗透系数值是已知的，对其进行普通的克里金插值获得初始渗透系数场（见图3），其与实际渗透系数场之间的RMSE记作R1，表示先验信息精度，此时的模型计算水位与实际水位还有较大差距。经过PEST 程序参数反演后，模型计算水位能够最大限度地拟合实际水位[12]，得到的参数场称为渗透系数估计场，与实际渗透系数场之间的RMSE记作R2，表示反演精度。模型计算水位与渗透系数值取自系统，误差范围为0.001。

图3 16个点(三角形)位置与初始渗透系数场(log K)Fig.3 The location of 16 points(triangles)and the initial permeability coefficient field(log K)

3 分析与讨论

为了研究观测井、向导点分布范围以及不同渗透系数初值对反演结果的影响，结合理想案例，分别设置不同分布范围的观测井和向导点模型及不同初值的初始渗透系数场模型，并对反演结果进行分析与讨论。

3.1 不同观测井分布范围反演结果分析

在参数估计中，观测井所包含的含水层信息越多，模型反演精度越高。为了研究不同观测井分布范围对反演结果的影响，将64 个向导点均匀分布在整个研究区，36 口观测井均匀布置在占研究区总面积16%、36%、64%、81%和100%的正方形范围内（如图4所示），正方形中心与研究区域中心重合。通过PEST 程序对初始渗透系数场进行反演求解，限于篇幅，仅给出观测井分布范围占研究区总面积16%、81%和100%的结果，分别见图5～图7。可以看出，当观测井布置范围适当时，反演结果较准确地反映了真实渗透系数场的空间分布，说明向导点法能够有效求解地下水反演中的不适定问题。

图4 观测井分布范围示意图Fig.4 Schematic diagram of the distribution range of observation wells

图5 分布范围为16%渗透系数估计场（log K）Fig.5 The distribution range is 16%of the estimated field of permeability coefficient(log K)

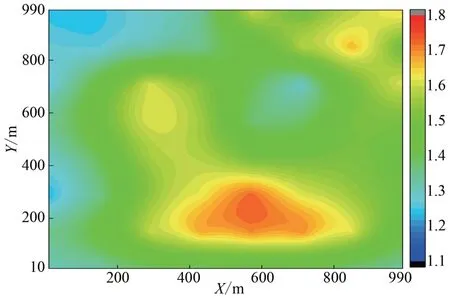
图6 分布范围为81%渗透系数估计场（log K）Fig.6 The distribution range is 81%of the estimated field of permeability coefficient(log K)

图7 分布范围为100%渗透系数估计场（log K）Fig.7 The distribution range is 100%of the estimated field of permeability coefficient(log K)

观测井不同分布范围情景下反演结果见表1。尽管初始渗透系数场与真实渗透系数场之间的R1 很小，甚至小于R2，但仍然不采用初始渗透系数场直接作为渗透系数估计场。这是因为本次理想案例中真实渗透系数场数据是已知的，仅作为参照场，可以计算出R1与R2值。而实际工程中的真实渗透系数场是未知的，拟合地下水水位反演后的也只是渗透系数估计场，无法计算R1与R2的值。

表1 不同观测井分布范围反演结果Tab.1 Inversion results of distribution range of different observation wells

观测井中实际水位与计算水位的RMSE变化区间为2.36×10-7～6.35×10-4，表明水位拟合十分良好。当观测井分布范围为16%时，R2值为0.447，反演效果最不理想；当观测井分布范围从16%增加到64%时，对应的R2 值依次减小(0.447>0.156>0.069)，说明随着观测井分布范围增加，获取的含水层参数信息增加，反演精度逐渐提高；当分布范围为81%与100%时，对应的R2 值为0.056、0.057，再次说明观测井分布范围增加到一定程度时，获取的含水层信息不再有太多变化，反演结果能够有效反映渗透系数场的空间分布，反演精度逐渐趋于稳定。

3.2 不同向导点分布范围反演结果分析

为了研究不同向导点分布范围对参数估计的影响，将36口观测井均匀分布在整个研究区，而64 个向导点均匀分布在占研究区总面积的16%、36%、64%、81%和100%正方形范围内，正方形中心依然与研究区域中心重合。

向导点不同分布范围情景下反演结果见表2。地下水位观测值与计算值的RMSE位于3.73×10-7～5.53×10-7之间，研究区水位拟合良好。当向导点分布范围为16%、36%，64%时，对应的R2值依次减小(0.194>0.065>0.045)；而当向导点分布范围为81%、100%时，R2 值分别为0.052、0.057，虽比64%对应的R2值0.045大，但增加幅度很小，基本保持稳定，说明增加向导点分布范围同样可以获得更高精度的渗透系数场。当向导点集中在部分区域时，获取的渗透系数参数信息较少，导致目标函数在负方向上步长变小，下降速率变慢。在本次模拟中，虽然目标函数初始值相同，但步长越小，达到目标函数要求所调用Modflow程序和优化迭代的次数就会越多[13]。

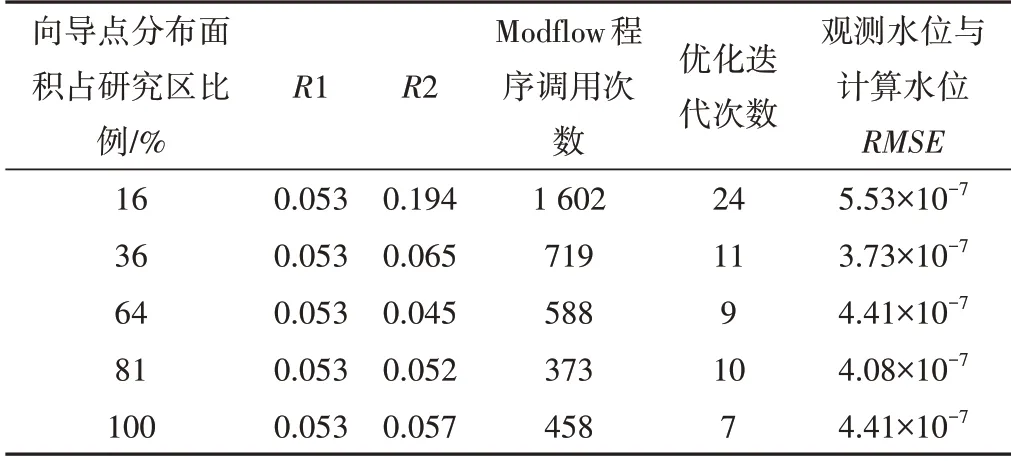
表2 不同向导点分布范围反演结果Tab.2 Inversion results of distribution range of different guide points

在参数化方法中，样本点的选取对参数反演结果影响很大，在研究区域内，抽样应该具有无偏性和一致性。当分布范围较小时，抽样数据集中在较小的范围，与真实渗透系数场和观测数据差距较大，无法代替整个参数组与观测组。随着向导点与观测井分布范围的增加，选择的样本区域扩大，尽管选择的样本数量不变但有效样本数增加，反演精度提高，R2 逐渐减小。随着分布范围接近整个研究区域，有效样本数目变化不明显，R2值基本保持稳定。

3.3 不同渗透系数场初值反演结果分析

为研究渗透系数场初值对反演精度的影响，将36 口观测井与64 个向导点分别均匀布置在整个研究区域内，在16 个已知渗透系数值点对数值的基础上增加0%、-10%、-20%、30%、50%、100%，重新进行克里金插值得到不同初值的初始渗透系数场，对应R1 值分别为0.053、0.151、0.297、0.466、0.768、1.527。

在此基础上进行反演，结果如表3所示。可以看出，观测水位与计算水位RMSE 值在3.33×10-7～4.71×10-7范围内，研究区水位拟合良好。R2 与R1 呈正相关，R1 值越小，R2 值也越小，拟合精度越高；反之，拟合效果越差。这是因为对于非线性问题，如果初始参数向量b0在参数空间中的位置与使目标函数最小化的最优参数向量b的位置相差较大时，参数估计问题容易陷入局部最优，使目标函数全局最小难以实现。同时由于模型要求b-b0尽可能小，目标函数的最小化需要反复迭代更新雅可比矩阵与向量b，即模型调用Modflow 程序与优化迭代的次数也会随着R1 的增加而增加。因此，初始参数向量b0越接近真实情况，反演精度越高[14]。

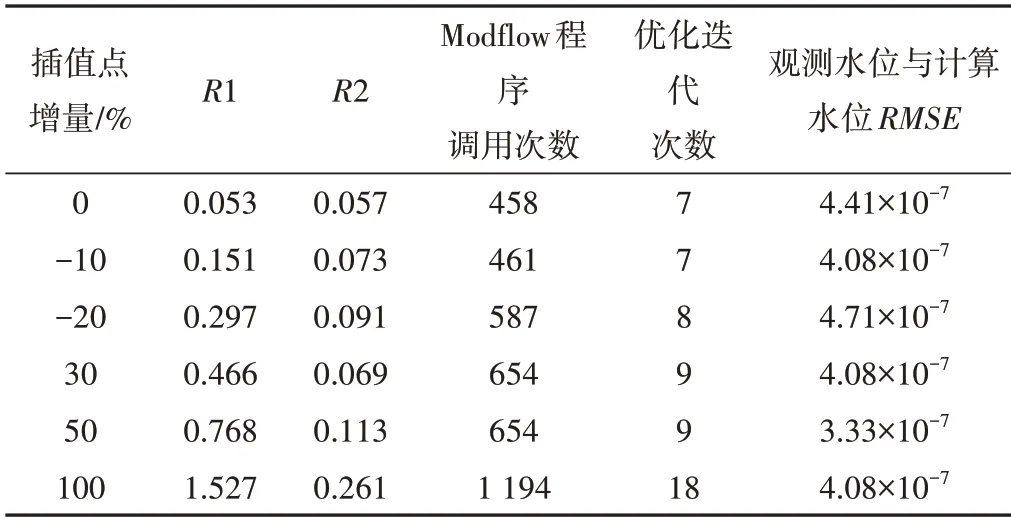
表3 不同初值的初始渗透系数场反演结果Tab.3 Inversion results of initial permeability coefficient field with different initial values

4 结 论

本文通过PEST 程序与地下水流模拟软件Modflow 耦合，对设定的理想算例进行渗透系数的高维反演，研究了向导点与观测井分布范围、渗透系数场初值对反演水文地质参数的影响，得出以下结论：

（1）向导点法是一种有效反演水文地质参数的方法，在参数反演应用方面具有较高的优越性，避免了人为概化分区的局限性，反演结果能较好地反映参数场的非均质性和空间结构。

（2）随着观测井分布范围的增加，参数反演精度逐渐提高并最终达到稳定，在观测井分布范围接近整个研究区域时达到最高。

（3）随着向导点分布范围增加，反演精度逐渐提高并趋于稳定，调用Modflow 程序和优化迭代的次数变少。向导点分布范围覆盖整个区域时，模型调用次数与优化迭代次数最少，此时该种布置方式较为简单，推荐实际工程中使用。

（4）采用向导点方法反演参数时，初始参数信息越接近真实情况，反演精度愈高。