红壤蓄水渗灌水氮入渗特征研究
裴青宝,廖振棋,余 雷,董文彪,陈鹏帆
(1.江西省水利科学研究院,南昌330099;2.南昌工程学院,南昌330099;3.西北农林科技大学水利与建筑工程学院,陕西杨凌712100)
0 前 言
红壤在我国南方丘陵区有较广的分布[1],是脐橙、柑橘等经济作物生长的重要载体[2,3]。脐橙、柑橘是需水量较高的水果品种,大部分种植地区虽然雨量充沛,但存在年际波动、季节性分布不均匀等问题(1961-2016年江西省气候时空变化特征)[4],容易造成季节性的干旱,同时还存在土壤结构性差、种植地区夏季蒸发量大等因素对实现脐橙、柑橘的稳产、高产带来一定的困难。随着脐橙、柑橘产业的快速可持续发展,以节水、高产和高品质为目标的生产模式成为必然选择[5]。脐橙、柑橘等作物采用不同类型节水灌溉技术时,受土壤自身特性等的影响,土壤水分湿润锋的运移及交汇规律具有较大差异,灌溉后其湿润体的形状和范围不尽相同[6-8]。针对红壤黏粒含量较高,水分养分不易渗入到深层土壤中的特点[9],拟将蓄水坑灌应用到脐橙、柑橘灌溉中。研究表明该种灌溉技术灌溉后湿润体的形状湿润锋的推进等均影响到了作物对水分、养分的吸收利用[10]。灌溉湿润面积和湿润深度应尽量与根系分布范围具有一致性,可以通过湿润锋的分布来判断灌溉水量的多少和灌水质量,但土壤质地、容重、含水量、灌溉水水质等均对湿润体特性有影响[11-13],各节水灌溉技术相对应的灌水器埋深、压力变化、开孔率等直接影响到作物对水分、养分的吸收利用[14-17]。蓄水坑灌、深层坑灌等作为坑灌的一种形式可将水分直接输送到作物根系附近,可有效地减少地表蒸发径流损失,提高水肥利用效率[18-20]。有研究发现土壤含水量与土层深度乘积与土壤硝态氮含量之间存在着极显著相关关系[21]。但目前在红壤区域针对蓄水坑灌技术的应用研究较少,红壤区水氮入渗影响因素尚不明晰。因此,本研究通过室内土箱试验,灌水量及埋深对单个蓄水坑灌红壤水氮分布的影响,以期为红壤丘陵区脐橙、柑橘蓄水坑灌技术应用推广提供理论支撑。
1 材料与方法
1.1 试验材料
供试红壤取自江西省赣南丘陵地区寻乌县澄江镇,于2019年4月在南昌工程学院江西省水工程安全与资源高效利用工程研究中心灌溉排水实验室进行试验,室内温度25~28 ℃,将土自然风干、碾压后,采用MS2000 型激光粒度分析仪测定,土壤自然堆积状态下粒径级0.02 mm<d≤2 mm、0.002 mm<d≤0.02 mm、d<0.002 mm 颗粒分别占28.52%、41.13%、30.35%,根据国际制土壤划分标准,属于黏壤土。试验土壤容重为1.39 g/cm3,初始土壤含水率5.6%、硝态氮量为18.68 mg/kg,铵态氮量为1.94 mg/kg。
1.2 试验装置与试验设计
试验装置如图1和图2所示,由马氏瓶,土箱、输水管、铁支架、水室、阀门等组成。土箱由有机玻璃板制成,尺寸为80 cm×50 cm×50 cm。灌水器采用内径为5 cm,高为20 cm,底部开孔率为40%,底部起曲面5 cm 高,开孔率为40%,上部曲面15 cm 不开孔。马氏瓶内装入配制好的KNO3溶液(814.5 mg/L),试验设定3 个不同灌水量分别为1、2、3 L,设定3 个不同灌水器埋深分别为10、15、20 cm设计方案见表1。
图1 试验土箱示意图Fig.1 Schematic diagram of test device
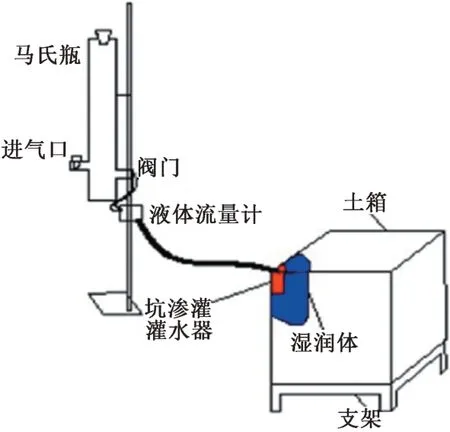
图2 单坑试验装置图Fig.2 Chart of single pit test device
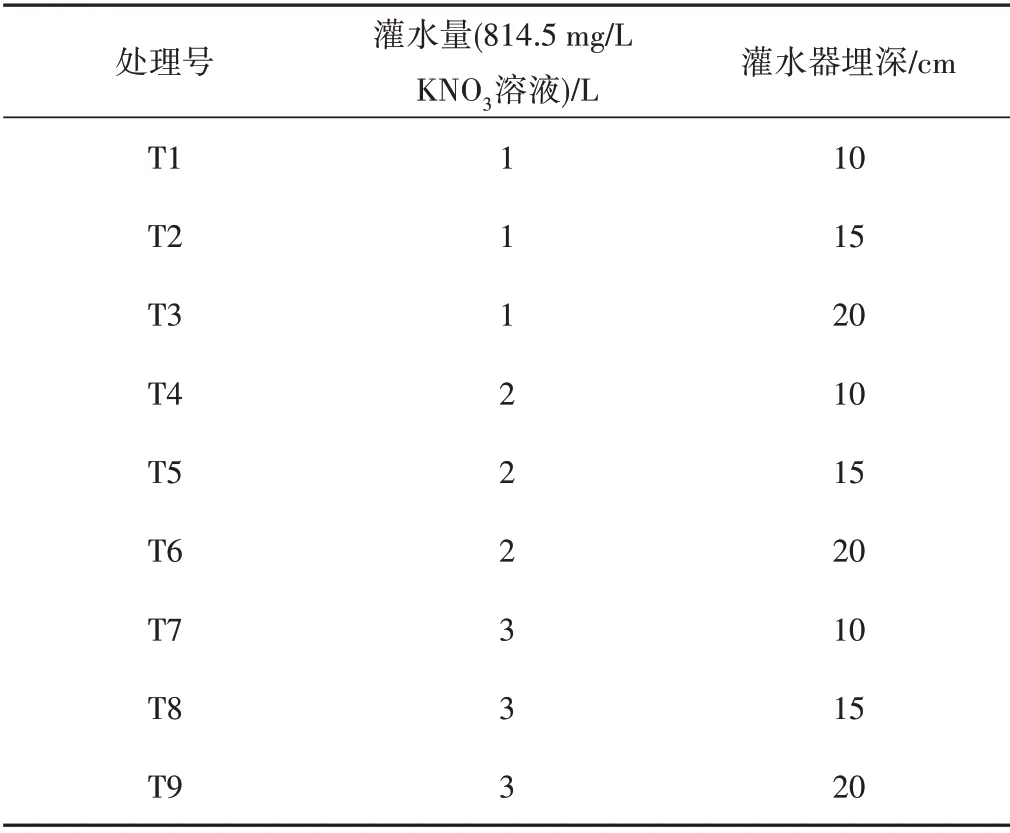
表1 试验处理Tab.1 Test treatment
按土样采集区平均干容重每层5 cm 分层装填土箱,每层用夯土器夯匀,层与层之间采用毛刷刷毛,填至灌水器埋设深度时,先将灌水器安装在土箱相应位置处,通过固体胶水将灌水器与土箱接触的缝隙闭合,并继续填土至设定位置。设定马氏瓶初始水头高于灌水器曲面开孔上端2 cm,试验在室内进行,无其他自然环境因素的干扰。待土箱填土自然沉降24 h 后开始试验;试验开始后,打开马氏瓶供水,入渗过程中记录马氏瓶读数,并间隔一段时间用记号笔在土箱侧面记录湿润锋的变化。9 个处理均设置3 次重复试验,数据取平均值,采用Microsoft Office Excel 2010 与Surfer 8.0 对数据进行处理。
2 结果与分析
2.1 不同灌水量与埋深条件下的入渗特性
如图3所示,红壤地蓄水渗灌0~10 min内平均入渗率为初渗率,10~200 min 之间入渗率逐渐降低,200~540 min 内平均入渗率为稳渗率。有研究表明[22],对初渗率的影响程度为土壤容重>土壤含沙量>土壤初始含水率>入渗肥液浓度;对稳渗率的影响程度为土壤含沙量>土壤容重>入渗肥液浓度>土壤初始含水率。而在不同入渗阶段对入渗率影响程度不同,入渗初期土壤沉降引起土壤孔隙度减少,对水土界面结构和水流入渗通道有一定影响;此时,渗入土体的肥液离子较少,离子置换作用小,对土壤颗粒吸附较弱入渗肥液对入渗率的影响较小。随着入渗时间延续,土壤湿润区不断向下扩展,湿润区内水势梯度差别减小,故不同灌水量下入渗初期初渗率相差较大,随着入渗时间的增加入渗率在短时间内快速减小,随之逐渐趋于一个稳定值,最后入渗率变化值逐渐趋于稳定,且接近于0值。
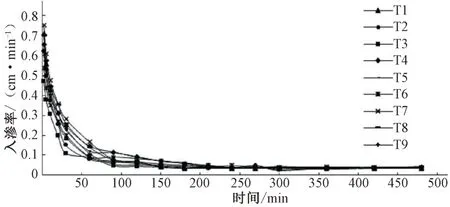
图3 入渗率变化曲线Fig.3 Variation curve of infiltration rate
由图3可知,各处理初始入渗率为:T7>T8>T4>T1>T9>T5>T2>T6>T3,各处理10~210 min 之间的入渗率大小为T7>T4>T1> T8>T5>T2>T9>T6>T3,这两个阶段灌水量对入渗率的影响均大于灌水器埋深的影响,同一埋深下,灌水量越大,入渗的影响越大;各处理间的稳渗率相差不大,其主要和土壤的自身入渗特性有关。
2.2 不同灌水量与埋深条件下湿润锋变化
由图4可见,垂向湿润锋运移距离随着灌水器埋深增加而减小,随着灌水量的增加而增加;在入渗160 min 内,垂向湿润锋的推进速度较快,随着入渗时间增加,湿润锋运移速率逐渐趋于平缓。在主要是因为在入渗前期,土壤水势梯度大,入渗较快;入渗后期土壤基质势的作用下,土壤入渗能力下降,这种差异逐渐弱化,湿润锋运移速率趋于一致。对不同灌水量和灌水器埋深下对单坑蓄水渗灌的垂向湿润锋运移距离与入渗时间进行幂函数拟合,即:
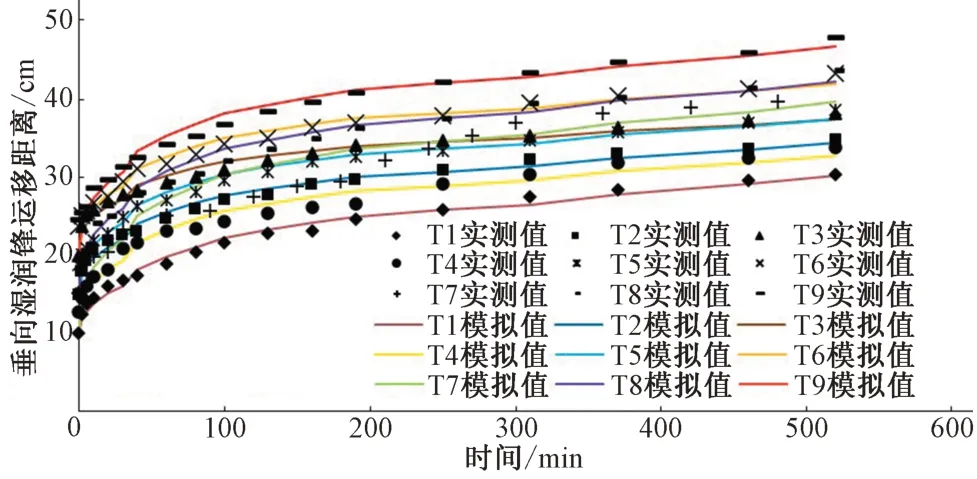
图4 垂向湿润锋随时间变化图Fig.4 Variation of vertical wetting front with time

式中:y为垂向湿润锋运移距离,cm;A、B为拟合参数;C为灌水器埋深,为10、15、20 cm。
由表2的拟合结果可知:各拟合函数相关系数均大于0.96,各参数拟合结果也较好,拟合参数A随着灌水量的增大和灌水器埋深的增加而增大。
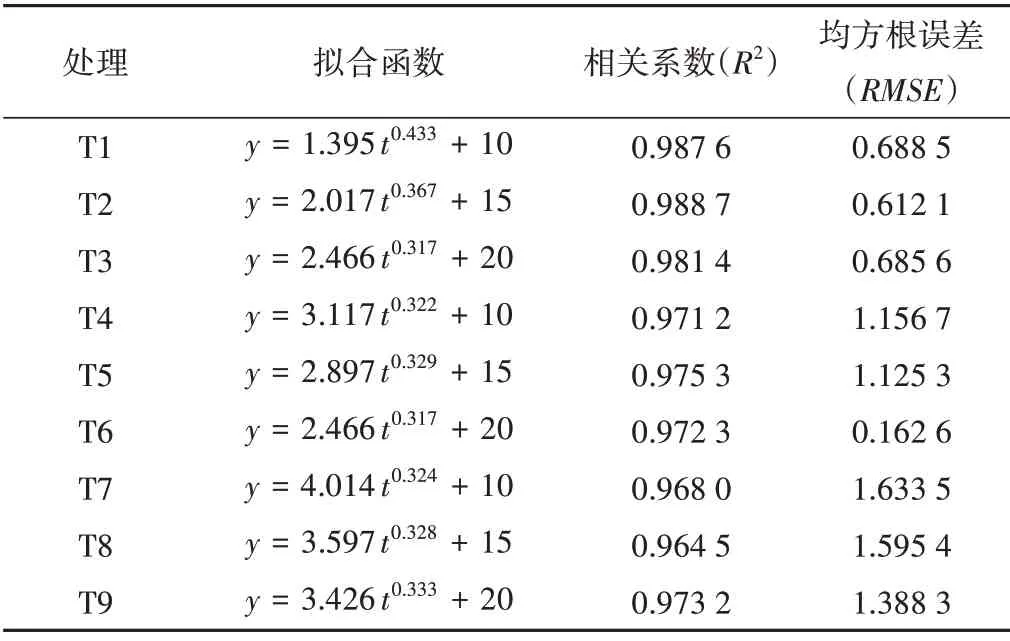
表2 垂向湿润锋运移距离拟合结果Tab.2 Fitting results of vertical wetting front migration distance
2.3 不同灌水量与埋深条件下湿润体内含水率分布
如图5所示,湿润体内含水率曲线都是以蓄水坑中心轴为中心的不规则1/4 椭圆形,表层含水率小,随着深度的增加含水率逐渐变大,在一区域达到峰值,然后又逐渐变小。不同处理下蓄水渗灌入渗后湿润体内含水率的分布表现为距离灌水器位置越远,含水率越小,等值线分布越密集,水势梯度也越小。灌水量越大,湿润体内高含水率区域越大,同一节点处的含水率也越大;随着灌水器埋深加大,湿润体范围向右下方移动。入渗结束后灌水器下方的土壤含水率随土壤深度增大逐渐变小,土壤含水率径向变化量为随着径向距离增加而减小,土壤含水率垂向分布与径向变化趋势相同。本试验设计的渗灌方式灌溉过程中水分不需要流经地表而直接通过坑渗装置侧壁流入中深层土壤减小了表层土壤的湿润范围,坑底的不透水性阻碍了水分的垂向直接入渗,迫使水分向蓄水坑周围运动。
由图5可见,随着灌水量的增加,土壤湿润范围增加,灌水器右下方湿润体内高含水率分布区域变大,土壤含水率为32%以上的分布面积越广。灌水量为1 L 时,土壤含水率为32%以上区域主要分布在灌水器下方0~25 cm、径向距离0~20 cm 范围内,含水率峰值为34%。灌水量为2 L 时,含水率为32%以上区域进一步扩大,主要分布在灌水器下方0~30 cm、径向距离0~25 cm范围内,含水率峰值为35%。灌水量为3 L 时,含水率为32%以上区域最大,主要分布在灌水器下方0~35 cm、径向距离0~30 cm范围内,含水率峰值为38%。
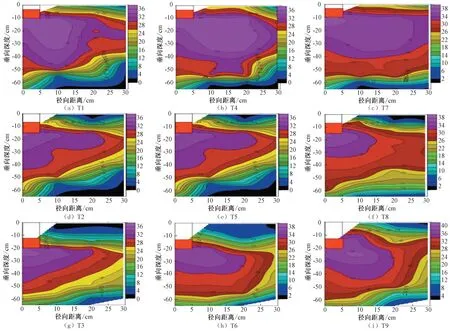
图5 土壤含水率分布图Fig.5 Distribution of soil moisture content
不同灌水器埋深的情况下,随着灌水器埋深的增加,含水率分布区域下移,高含水率区域主要分布在灌水器下方0~20 cm。且同一灌水量下,土壤最高含水率随灌水器埋深的增加有减小的趋势。处理T7、T4、T1 在各相同灌水量条件下呈现出具有较高含水率范围的状态,其中一处理T7最大。
2.4 不同灌水量与埋深条件下湿润体内硝态氮分布
从图6可见,湿润体内硝态氮垂向分布范围基本相同,土壤硝态氮含量等值线均以蓄水坑为中心轴的不规则椭圆。同一灌水量时,灌水器周边硝态氮含量变化梯度相对均匀,纵向分布规律与径向分布规律近似一致。不同坑深时,硝态氮等值线的垂向分布均随土壤深度的加深先增大后减小,距离灌水器径向距离较远处断面的土壤硝态氮存在较大的波动。各处理湿润体内硝态氮峰值均随灌水量的增大而增大,且出现硝态氮含量峰值随灌水量的增大在土体内下移的现象。

图6 土壤硝态氮分布图Fig.6 Distribution of nitrate nitrogen in soil
在不同处理下对湿润体内层厚为5 cm 土层硝态氮浓度分布状况进行方差分析和回归分析。由表3的多因素方差分析表明,土层深度变化对土壤硝态氮浓度变化规律影响较为显著(P<0.05),灌水量变化对土壤硝态氮浓度变化规律影响较为显著(P<0.05),径向距离变化对土壤硝态氮浓度变化规律影响较为显著(P<0.05)。峰值处溶质主要受溶质势和重力势作用向土壤深层运移,峰值位置也由右下方运移,使得该两层土壤硝态氮浓度受灌水量影响显著。硝态氮峰值受灌水器影响较为显著(P<0.05),不同灌水量之间的硝态氮峰值含量浓度差异显著(P<0.05)。随着入渗时间的增加,土壤中对流作用减弱,在分子扩散作用与机械弥散作用下,溶质随水分向土壤中深层运移。故土壤深度、径向距离、灌水量的变化对土壤硝态氮的分布均有显著影响,影响程度为:灌水量>土层深度>灌水器埋深>灌水量×灌水器埋深>土层深度×灌水器埋深>土层深度×灌水量>土层深度×灌水量×灌水器埋深。
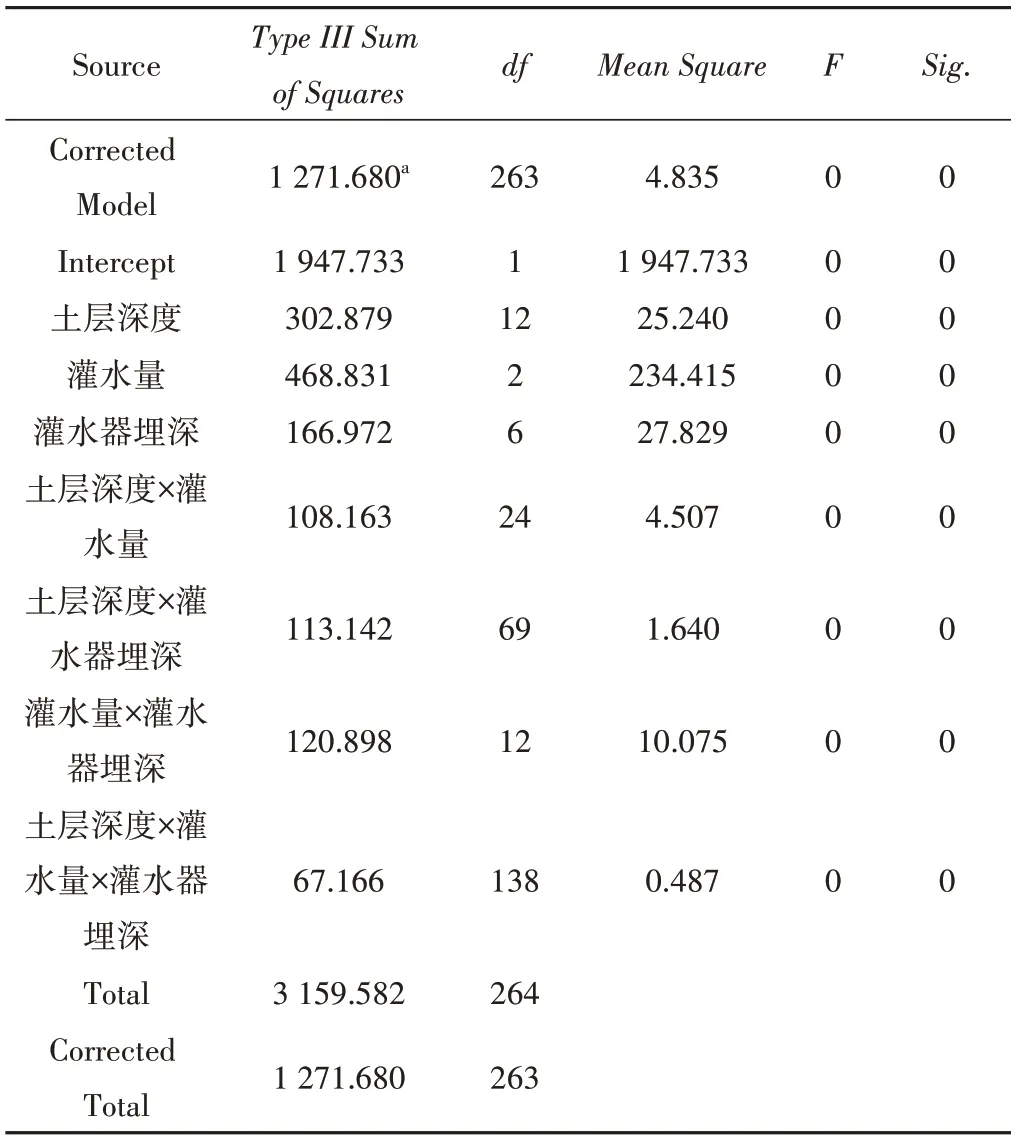
表3 方差分析Tab.3 Analysis of variance
3 讨 论
3.1 灌水量与埋深对入渗特性的影响
研究表明土壤入渗过程入渗率均随入渗时间推移经历快速减小、逐渐减小和趋于稳定的3 个阶段[23]。风干后的土壤的初渗率在入渗初期很大,随之在较短的时间快速降低,最后趋于稳定[24],本次实验红壤地区蓄水渗灌入渗率也呈现相同变化过程。
同一灌水量下,硝酸钾溶液入渗率随着灌水器埋深而减少;在同一灌水器埋深情况下,硝酸钾溶液入渗率随着灌水量的增加而增加;具体体现在硝酸钾溶液的硝酸根离子的作用,由于各个胶体之间相互吸引从而凝聚成较大的粒子,从而形成团聚体,增大了土壤颗粒的粒径,使得土壤结构变松散,土壤孔隙变大,土壤曲折系数减小,土壤水分运移时所遇到的阻力变小,使其入渗率变大,从而促进硝酸钾溶液入渗,而灌水量增加,越促进硝酸钾溶液的入渗,入渗率差异性越明显。
3.2 灌水量与埋深对含水率分布的影响
土壤吸力和重力是土壤水分运动的两种驱动力[25],即土壤的基质势和重力势作用。在开始入渗时,土壤的基质势作用占主导作用,重力势作用相对较小;由于在均质土壤中入渗,因此在径向和垂向上的土壤基质势作用相同。但由于侧面开孔率略高于底部开孔率,因此在入渗初期,土壤水分径向运移速度比纵向运移速度略快。随着灌水历时推移,土壤含水量逐渐增大,土壤的基质势作用减弱,重力势在驱动土壤水分运移中逐渐起主要作用,土壤水分在垂向的入渗的速度开始明显大于径向。当马氏筒瓶内的水量入渗完后,即进入土壤水分非恒定入渗阶段,此时土壤的入渗率趋于稳定,灌水器的水量也逐渐减小,直至灌水器的水分全部入渗完毕。当灌水器内的水分全部入渗后,就进入再分布阶段。由于灌水器周边的含水量比湿润锋处的含水量高,即灌水器附近的势能比湿润锋附近的高,高含水量的处水分在势梯度的作用下扩散至低含水量处。在湿润体径向和垂向的同一位置处,土壤含水率随灌水历时的增大而增大。入渗开始后,灌水器周围的土壤含水率在较短的时间内达到或接近饱和,所以在同一时刻,随着径向距离、垂向距离的增加土壤含水率由饱和含水率逐渐减小至初始值。
3.3 灌水量与埋深对灌硝态氮分布的影响
由图6可见,不同灌水量时,湿润体内硝态氮浓度随入渗时间的增加而逐渐累积增加,且灌水量不同硝态氮的累积量不同,灌水量越多时,硝态氮含量越大。土壤硝态氮的再分布规律为由灌水器周边至湿润体边缘呈现“低-高-低”的分布态势。这与张微笑等人的研究结果相似[26-28]。
硝态氮的主要运移方式是对流,使得在湿润体边缘有大量累积。坑壁附近范围由入渗刚开始时,土壤为初始含水率,坑壁附近的水势梯度大,水流的流速比较大而易于随水分运移从而造成了这个区域的淋溶损失,入渗中期该区域土壤的含水率高,较高的湿度致使土壤的通透性差,土壤处于还原条件使得反硝化作用加强,在反硝化细菌作用下产生亚硝酸和游离态氮,造成一定硝态氮的损失,此外还有很多因素会影响硝态氮的分布,在有氧条件下,在硝化细菌的作用下发生硝化作用,而影响硝化细菌活性的因素包括土壤有机质含量、土壤水分、含氧量、pH 等,这些因素的变化都会影响到硝化过程进而影响硝态氮的含量、分布。而在无氧的条件下还会发生反硝化作用,从而影响硝态氮的浓度的分布。硝酸根离子由于带负电荷,与土壤胶体所带电荷相同,故不易被带负电荷土壤胶体吸附,具有较强的移动性。
4 结 论
(1)灌水量与灌水器埋深均对红壤蓄水坑灌入渗率有影响。在达到稳定入渗阶段之前,灌水量对入渗率的影响大于灌水器埋深的影响;垂向湿润锋运移距离随着灌水器埋深增加而减小,随着灌水量的增加而增加;垂向湿润锋运移距离与入渗时间之间有较好的幂函数关系,系数A随灌水量与埋深的增加而增加。
(2)灌水量越大,土壤湿润范围增加,高含水率区域越大,湿润体内同一节点处的含水率也越大;随着灌水器埋深加大,湿润体范围向右下方移动;入渗后灌水器下方的土壤含水率随土壤深度增大再逐渐变小,土壤含水率径向变化量为随着径向距离增加而减小,距离灌水器位置越远,含水率越小,其等值线分布越密集,水势梯度也越小。
(3)相同灌水量下,硝酸钾溶液入渗率随着灌水器埋深而减少;在相同灌水器埋深情况下,硝酸钾溶液入渗率随着灌水量的增加而增加。灌水量不同硝态氮的累积量不同,灌水量越大时,硝态氮含量越大。土壤硝态氮的分布规律为由灌水器周边至湿润体边缘呈现“低-高-低”的分布态势。各处理土壤硝态氮含量峰值均随着灌水器埋深的增加而逐渐下移;随着灌水量增加,土壤硝态氮含量峰值范围也扩大。对土壤硝态氮的分布显著影响为:灌水量>土层深度>径向距离>灌水量×径向距离>土层深度×径向距离>土层深度×灌水量>土层深度×灌水量×径向距离。

