科技评价中的TOPSIS的权重单调性漏洞的修正①

崔庆宏, 李 敏, 陈雨田

(青岛理工大学管理工程学院,山东 青岛266520)

0 引 言

TOPSIS方法是目前应用最广泛的决策方法,自Hwang等提出以来,广泛应用于经济、科技、社会、管理等各个领域[1]。传统TOPSIS法由于权重事先给定使得评价结果具有一定主观性,一部分TOPSIS评价模型对权重设定方法进行了改进,但大多数方评价法中都涉及到了权重。权重确定的科学性和合理性是科技评价中的基础问题,直接影响科技评价工作的有效进展,因此,研究TOPSIS的权重单调性对科技评价的影响具有十分重要的意义。通过对TOPSIS法的权重单调性的漏洞进一步分析,对TOPSIS法的相对贴近度的计算公式加以改进,提出欧式距离TOPSIS法,并以SCI数据库收录的JCR2019土木工程学期刊为例将改进模型应用于评价,验证该方法的有效性。

1 文献综述

TOPSIS方法在科技评价研究中得到了广泛应用,但其自身仍存在一定的局限性,其存在逆序、权重取值主观化、欧氏距离失效[2]等问题。相关学者围绕这些TOPSIS方法存在的问题进行了优化研究。马奇飞扬等[3]利用改进的TOPSIS法克服了评价结果中存在逆序现象的问题。陈为公等[4]借鉴模糊理论对TOPSIS方法进行改进,运用三角模糊数完成对定性指标的定量化表达,解决多目标多属性的评价难题。陈为公等[5]引入向量夹角余弦对TOPSIS方法中的欧式距离进行改进,修正了当属性变量间具有相关性时欧氏距离失效的漏洞。综上所述,从目前对TOPSIS法的研究看,学者们对TOPSIS权重的单调性漏洞并没有深入研究。TOPSIS方法如果不具备权重的单调性,就无法保证TOPSIS法的有效性,即会使重要的指标往往被忽略而得不到重视。俞立平[6]通过对TOPSIS法权重单调性的验证,得出TOPSIS存在权重单调性漏洞。

鉴于此,通过对TOPSIS法的权重单调性的漏洞研究,基于欧式距离TOPSIS法,对TOPSIS法的相对贴近度计算公式提出了改进,修正TOPSIS法中权重单调性的漏洞,保证TOPSIS方法的有效性。

2 研究设计

2.1 数据来源

选取SCI数据库收录的JCR2019土木工程学刊物作为研究对象来实证检验欧式距离TOPSIS法的权重单调性。SCI数据库收录的JCR2019土木工程学刊物共有134种,由于部分期刊存在数据缺失现象,因此,对其进行筛选,经过处理后留有121种期刊进行研究。

选取JCR2019公布的7个评价指标分别是:总被引频次X1、影响因子X2、5年影响因子X3、即年指标X4、被引半衰期X5、引用半衰期X6、特征因子得分X7,其中被引半衰期X5、引用半衰期X6属于成本型指标,剩余其它指标属于效益型指标。

如表1所示是各指标数据的描述统计,除了即年指标为负偏态分布外,其它所有指标均为正偏态分布,以及除引用半衰期接近正态分布外,剩余指标K-S的显著性均为P＜0.05,即正态分布的原假设均不成立,说明原始数据不服从正态分布。非正态分布的指标数据并不能直接进行参数检验,即不能直接进行岭回归,需要对数据进行取自然对数的处理来改善数据的偏倚问题,使得数据分布更加偏向正态分布,并且使模拟的实际权重更加精确。

表1 指标数据的描述统计

通过对传统TOPSIS法及提出的欧式距离TOPSIS法进行对比分析论证,为了使研究结果更加可靠和稳健,分别选取具有代表性的效益型指标为影响因子和成本型指标为引用半衰期进行研究,采取5次变权重实验来计算各个指标的模拟权重和评价结果,更好地研究权重单调性漏洞,并找到解决TOPSIS法权重单调性漏洞的方法。

2.2 权重单调性的检验方法

2.2.1 传统TOPSIS法计算分析

传统TOPSIS方法计算公式:

公式(1)中,当设计权重W k增大时,根号里的分子和分母的权重都会提高。既然无法通过数学公式直接证明评价结果随着权重的增加而增大,那么可以通过反推法,假设传统TOPSIS存在权重单调性的前提下,反推出评价结果与权重正相关的成立条件,从而进一步说明如果要满足传统TOPSIS的权重单调性,需要一定的判断条件,而不是适用于所有情况。具体推理过程如下:

(W k＞e＞0)其中设定:

那么

e表示权重的变化值,ΔT=T i-T i',另ΔT＞0,ΔU=U i-U i',则只需ΔU＜0,再另ΔY=ad-bc,使ΔY＜0,即时,才能满足ΔT＞0,也就是传统TOPSIS权重单调性才能够成立。

2.2.2 权重单调性的检验步骤

(1)实际权重计算方法

由于无法直接从TOPSIS计算公式推导出其余指标权重不改变的条件下,其中一个指标的实际权重会因为设计权重的增加而增大,进而评价结果也增大。所以借鉴俞立平等提出来的用回归分析进行实际权重的模拟[6]。因为作为研究对象的学术期刊,评价指标一般具有一定的多重共线性,所以采用岭回归来提高计算的精度:

把回归系数C j进行标准化处理,计算出各指标的模拟权重:

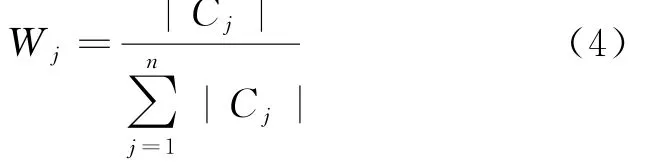
(2)设计权重计算方法

为了便于研究,设定被研究对象的指标的权重W k大小依次为1～5,其他指标权重取值均为1,共有n个指标,那么剩余指标权重之和为n-1,所有权重之和为n-1+W k,则X k的设计权重计算公式为:

设计权重计算结果如表2所示。

表2 设计权重

(3)设计权重对实际权重的计算方法

按照公式(1),通过改变被研究对象的权重W k,计算出评价得分T i,然后根据实际权重的计算方法,依次得出5个设计权重的实际权重。

(4)分析设计权重对实际权重的影响

将模拟出的实际权重进行从小到大排序,分析比较实际权重是否与设计权重的排序一致。假设模拟权重与设计权重是正相关,并且满足评价结果随着权重的提高而增大,表明传统TOPSIS方法具有权重单调性;假设模拟权重与相对应的设计权重排序不一致,出现逆序现象,即设计权重增加,模拟权重反而有降低的情况,或者有出现评价结果与权重是负相关的情况,说明传统TOPSIS评价方法存在漏洞。

2.3 权重单调性漏洞的修正方法

考虑到TOPSIS非单调性的原因是对分子和分母中的欧式距离都有加权,所以提出对评价结果公式改进,即把每个评价方案与最优理想解的距离差作为新的属性值,同时对欧式距离也进行改进,采用取绝对值的原理来代替之前先求平方和再进行开方的复杂计算,改进后的欧氏距离不仅便于计算,而且可以对有相似性的属性值更加有效的辨别,即:

β表示决策者对于收益型和成本型的偏好程度,β＞0.5,表示决策者偏向于收益型,β=0.5,表示决策者对收益型和成本型偏好相当,β＜0.5,表示决策者偏向于成本型。以研究权重单调性的问题为重点,所以β取0.5。很显然,改进后的TOPSIS公式完全满足权重单调性的条件。由于优化方法是针对欧式距离概念上的改进,因此也称为欧式距离TOPSIS法。

3 研究结果

3.1 传统TOPSIS法评价结果分析

3.1.1 影响因子的实验结果

其余指标的设计权重都取1,影响因子权重W取值分别取1～5,运用传统TOPSIS计算,评价结果如表3所示,因为受篇幅限制,表3只公布了原始JCR数据列表中有权重单调性问题的部分刊物。分析列表中的评价值可以明显地得出,评价值随权重单调递减。

表3 TOPSIS期刊影响因子评价结果(部分)

通过对指标数据进行岭回归分析后,按照公式(4)对回归系数进行标准化处理,计算出各指标的模拟权重,随着W取值的增加,模拟权重依次为0.057,0.092,0.117,0.137,0.153,呈现单调递增的变化趋势。

3.1.2 引用半衰期的实验结果

为了使研究结果更具说服力,再以成本型指标引用半衰期为例,把研究对象换为引用半衰期,其研究方法与影响因子相同,选取有权重单调性问题的4种期刊分析,其中一些期刊的计算结果如表4所示。分析列表中的数据,可以明显地得出,评价值与权重不具有单调性,存在有降低和相等的情况。

表4 TOPSIS期刊引用半衰期评价结果(部分)

在对数据进行岭回归分析后,同样按照公式(4)对回归系数进行标准化处理,得到各指标的模拟权重,随着W取值的增加,模拟权重依次为0.117,0.153,0.180,0.203,0.222,权重单调递增。

为了进一步地研究,把以上影响因子和引用半衰期的实际权重与设计权重展开对比,如图1所示,首先,可以直观地看出随着权重W k的增加,影响因子和引用半衰期的模拟权重也随之增加,但通过二者指标的评价结果如表3和表4所示,可以明显地看出权重增加后,评价结果反而有下降或相等的情况,而不是与权重正相关,这说明传统TOPSIS不具有单调性。其次,可以发现实际权重没有完全体现出设计权重的重要性,而是被缩小。在权重W k变化相同的条件下,实际权重提高的速率低于设计权重的增速,这说明TOPSIS权重具有一定的冗余度。

图1 TOPSIS设计权重与实际权重

3.2 欧式距离TOPSIS法评价结果分析

为了增加研究结果的可靠性,仍然以影响因子和引用半衰期为例通过公式(6)计算,最终得到表5影响因子和引用半衰期的评价结果,以及表6和图2的影响因子、引用半衰期的实际权重。由于重点是研究权重单调性问题,所以β取值为0.5。

如表5中针对采用传统TOPSIS法后存在权重单调性问题的部分期刊进行对比分析,对影响因子评价指标和引用半衰期评价指标的W分别取值为1,2,3,4,5。通过分析列表中的结果,得出评价值随权重单调递增。

表5 欧式距离TOPSIS影响因子和引用半衰期的期刊评价结果(部分)

如表6中,当权重W k依次增大时,影响因子和引用半衰期的实际权重也随之增大,并且通过表5的分析数据看出评价结果也都普遍地随着权重W k的增加而增大,这说明修正后的欧氏距离TOPSIS符合单调性的条件,即具有权重单调性。如图2中可以看出欧氏距离TOPSIS的权重也具有冗余度。通过5次试验,设计权重平均值是0.442,影响因子实际权重平均值是0.157,占设计权重的49.65%,引用半衰期实际权重平均值是0.184,占设计权重的58.32%。

图2 欧式距离TOPSIS设计权重和模拟权重

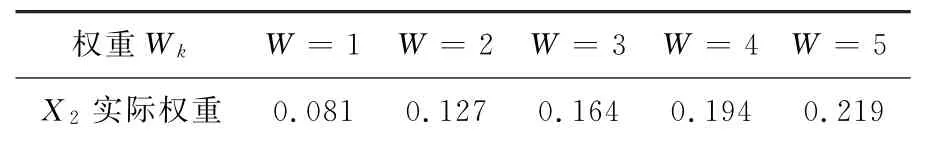
表6 欧式距离TOPSIS模拟权重

?

4 结 论

基于SCI数据库收录的JCR2019土木工程学刊物的数据,以影响因子和引用半衰期为例,运用改进欧式距离TOPSIS法,对TOPSIS权重单调性漏洞修正,得到如下主要结论:

1)改进欧式距离TOPSIS法修正了TOPSIS法权重单调性漏洞。提出了改进欧式距离TOPSIS评价方法,在进行评价时,把每个评价方案最优解的距离差作为新的属性值,采用绝对值的原理代替之前求平方和再进行开方的复杂计算,通过线性加权的方法,引入属性偏好值β,得到每个方案距离最优方案的加权距离,从而修正了权重单调性的问题。

2)TOPSIS法和改进的欧式距离TOPSIS法对设计权重均有缩小的作用。通过5次试验,发现TOPSIS法和改进的欧式距离TOPSIS法的实际权重都不能真实反映设计权重的大小,反而缩小了设计权重。TOPSIS法中,影响因子的均值占设计权重的35.17%,引用半衰期的均值占设计权重的55.34%;欧式距离TOPSIS法中,影响因子和引用半衰期的均值分别占设计权重的49.65%和58.32%。由此可见,TOPSIS法要比欧式距离TOPSIS法的缩小作用更加明显,欧式距离TOPSIS法可以进一步改善这种冗余度。