地铁盾构施工过程中变形与结构失效机制研究①
林珍伟, 董桔灿, 欧建良, 肖勇杰
(1.阳光学院土木工程学院,福建 福州350015;2.深圳市高速工程顾问有限公司,广东 深圳518029)
1 地铁盾构隧道结构
1.1 管片结构
盾构结构中,盾构管片作为地铁盾构施工中的最基础的结构件,与工程的安全性息息相关[1]。盾构管片在施工过程中会受到来自土层的压力、地下水带来的压力以及施工过程受到的部分特殊作用力和载荷的影响。不同管片由于材料的不同,其生产工艺质量要求以及成型后的物理性质都差异极大。从生产工艺方面来说,金属材料即钢材和铸铁材料在焊接过程中应严格遵守工艺标准及工艺纪律,来保证焊接的变形量符合标准。
1.2 接头构造
无论是通缝拼接还是错缝拼接,通常为了提升结构的强度,会在节段的环形表面的中间设置一个凸榫,它不仅极大地提高了环形表面抗弯曲抗剪切的能力,而且使整个环形的平面度更以保证,也便于施工。在管片之间接触的外弧面加工出槽,便于弹性密封垫的安装;在管片之间接触的内弧面也加工出嵌缝槽,保证连接的紧密[2]。此外,在环向管片连接处用螺栓连接,来增强连接的强度,在管片纵向连接处,除了强度足够的螺栓连接,还应在管片端接触的肋纵缝中加工出相对窄的凹凸榫槽;在管片的连接处,设置环向的螺栓连接,除了能保证环向连接的可靠外,环向螺栓连接的大大减少管片之间纵向的变形与缝隙[3]。
2 地铁盾构隧道施工引起的变形模式与特点
2.1 纵向变形
2.1.1 整体变形
隧道整体纵向变形主要表现为整体下沉和倾斜两部分,可表示为式(1)。
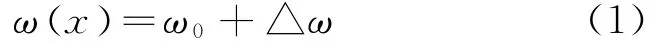
式(1)中:ω0为隧道的整体下沉变形量,△ω为隧道的倾斜引起的纵向变形量。
当隧道的产生整体变形时,隧道的压扁效应与纵向剪切传递效应无法对隧道整体结构产生附加效用。然而,当隧道的边界约束或地基的条件沿隧道的纵向方向变化时,隧道也将在整体变形的条件下承受额外的载荷。
2.1.2 隧道推进时的指数型变形模式
在盾构掘进的过程中,随着下卧土层的变化,衬环也会产生下沉。由于土层及其他情况的差异,盾构尾部后不同位置的衬砌沉降也会不同,这就导致了纵向变形的产生。结合某地区盾构施工实例,盾构在顺利推进过程中隧道曲线模式表现为双曲线或指数型曲线,这两种形式类似,故文章以指数型曲线为例进行介绍,如式(2)所示。
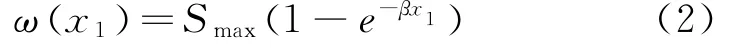
式(2)中:引入的参数β取值范围在0.005~0.02之间,其大小与隧道施工过程中的施工参数等相关;Smax表示隧道沉降变形量的最大值,其取值范围为10~130mm;x1表示变形处距盾尾的距离。
2.1.3 隧道纠偏变形模式
盾构曲线推进与纠偏推进情况下,由于千斤顶的偏心荷载作用,隧道纵向变形曲线可表示为式(3)。

2.1.4 其它纵向变形模式
在地铁施工过程中,盾构结构还会由于地形等多方面因素的影响产生其他方面的纵向变形,如会受到附近施工工程的影响产生纵向变形,这种情况,通常利用高斯曲线来模拟其变形曲线。此外,地铁隧道还会因其长期沉降而产生纵向变形等。
2.2 横向收敛变形
为方便横向变形量公式的推导,将盾构隧道假设为质量以及截面均匀的梁。通过分析,隧道在施工过程会受到纵向弯矩M的影响,隧道纵向方向则会受到纵向的力P的影响(见图1)。

图1 弯曲条件下衬砌内力分布图
假设隧道的厚度为T,作用在其方向上的竖直纵向的等效应力为σx,则如式(4)。

如图1所示,由于隧道弯曲变形的影响,则其纵向内力P并不是完全水平,因此,隧道由于力的平衡会产生力V,其方向如图所示,其大小与P相关,如式(5)。

式(5)中,θ为隧道的纵向单位所产生的弯曲角度,由于其足够小,在这里将其视为无穷小,则满足式(6)。

因此式(5)转变为式(7)。

在工程计算中,由于变形相对工程结构较小,通常用隧道的变形曲率κ来指代隧道实际的弯曲变形,而单位长度上的弯曲变形角度为曲率κ的定义,如式(8)。

同样,因为θ足够小,则式(8)可视为κ≈θ,假设隧道只产生弯曲变形,则其堆彻等效应力为式(9)。

式(9)中,I c为施工隧道计算点处横截面惯性矩,由于均质假设I c为固定值,仅与隧道尺寸有关;y为变形分析点距中性轴的长度,将式(9)代入式(7),求得径向附加力,得式(10)。

式(10)中:α为变形分析点与竖直方向的夹角,r为施工隧道的半径。
根据图1中受力情况,推导其横向变形为式(11)。

压扁载荷下的横向内力为式(12),(13),(14)。

式(12),(13),(14)中:M a为压扁荷载引起的衬砌弯矩,N a为压扁荷载引起的衬砌轴力,Q a为压扁荷载引起的衬砌剪力。
在隧道物理模型建立时候,将隧道视为形状质量均匀的圆管,由于现实条件的差异,隧道的接缝并不均匀,其闪缝以及纵向错台会对隧道的整体刚度降低,因此,引入常数η,常数η的大小由经验可得,因此,式(11)转化为式(15)。
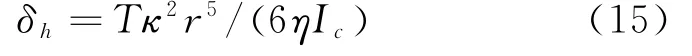
然而,实际上的隧道的横向变形相对于式(15)的计算结果来说,要小一些。这是因为没有考虑到土层的约束作用。根据winkler地基模型,假设土体抗力p k的分布形式为三角形,且均匀分布在隧道两侧水平直径上下各π/4的范围内,则如式(16)。

其中,k为土体抗力,土体抗力会对隧道产生变形,由土体抗力产生的水平方向变形为式(17)。

因此,由土体抗力引起的隧道的横向变形量为式(18)。
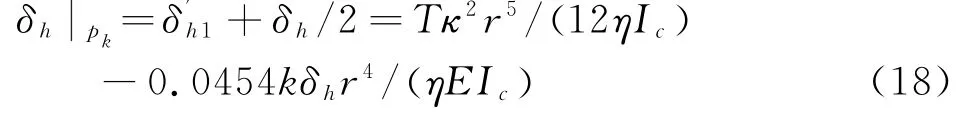
因此,考虑土体抗力影响的隧道水平方向产生的变形量应为式(19)。

由抗力产生的隧道收敛为式(20)。

假设隧道最初并非水平,而是具有一定的曲率,将这一曲率视为初始曲率κ0,则隧道受到压扁效应影响后,其整体的弯曲变形角度为θ,是θ0与θi之和,θi是隧道的纵向弯曲所引起的变形角度,如式(21),(22)。

式(21),(22)中:κi为由于隧道纵向弯曲而产生的附加曲率,由此得式(23)。

将式(21),(22),(23)结合起来,得到隧道弯曲引起的横向变形如式(24)。

综合考虑以上因素,隧道衬砌内力分别为式(25),(26),(27),(28)。

3 地铁盾构隧道施工的结构失效机制
3.1 隧道环缝和纵缝张开失效
盾构隧道在施工以及养护过程中,因为隧道的缝隙导致隧道失效的状况比较普遍。由于盾构隧道施工的实际情况,由于其变形和受力都较为复杂,在上述分析计算中,将隧道视为具有等效连续弯曲变形的基础梁。因此,隧道拼缝张开量也是评价隧道变形是否在安全状态的必要标准。隧道盾构管片之间接口的螺栓变形对隧道失效的影响要远大于管片本身变形的影响。
3.2 螺栓剪断失效
盾构结构中螺栓的强度与隧道的安全性细细相关,螺栓的强度不足除了容易造成螺栓纵向的拉伸导致隧道间缝隙增大外,还有一种情况,其危害性远远大于自身纵向拉伸变形。这种情况就是接头处螺栓连接由于其复杂的受力环境下,受到较大剪切力的影响,若剪切力足够大,螺栓就有剪断的风险,这种情况一旦发生,对会大大衰减隧道的安全性以及寿命。
3.3 接缝渗漏水失效
盾构结构的隧道的渗水漏水是最常见的问题之一,造成渗水漏水的原因除了由于隧道缝隙过大外,更多的原因是施工不规范的原因。
在盾构隧道的施工中,如果管片拼装环节未严格按照有关规定施工。在安装过程中管片会造成碰撞,对止水带的功能造成影响,严重时会造成止水带的脱落。由于施工现场众多因素的影响,盾构施工的实施难以保证快速又准确,可能施工过程中由于疏忽产生较大的错台,这可能导致管片开裂,变形,滑动,进而造成漏水渗水现象。
4 结 语
在地铁盾构施工中,由于管片间缝隙过大、渗漏造成失效的事例比比皆是。隧道施工过程中,其变形的最大曲率出现在盾构结构的尾处,因此压扁效应影响最大的位置也在此处。此外,还结合人为因素,对隧道环缝纵缝张开失效、接头螺栓剪断失效、漏水等情况进行了分析。防止地铁盾构施工过程中变形与结构失效除了应选取合适的管片接头方式外,还应在设计中考虑到其纵向变形横向变形的影响。

