Order Allocation in Industrial Internet Platform for Textile and Clothing

XU Chunxiao(徐春晓)， LIU Guohua(刘国华)， MA Yao(马 耀)， HU Tianwei(胡天伟)

College of Computer Science and Technology, Donghua University, Shanghai 201620, China

Abstract: In order processing in the industrial Internet platform for textile and clothing, assigning optimal order quantities to each factory is the focus and the existing difficulty. The order allocation is a typical NP-hard problem in combinatorial optimization, and typical research of this kind is still at the initial stage. This paper aims to improve the optimization approach to select factories and to allocate proper orders to each one. It designs a genetic algorithm by making a deviation constraint rule for the initial population and introducing a penalty function to improve convergence. Remarkably, the objective functions of total cost along with the related constraints undergo optimization in the model. The experimental results indicate that the proposed algorithm can effectively solve the model and provide an optimal order allocation for multi-factories with less cost and computational duration.

Key words: industrial Internet; order allocation; heuristic algorithm; goal optimization

Introduction

With a new era of deepening scientific and industrial revolution, digital and electronic techniques have been applied in traditional industries. Indeed, strengthening the digital transformation of industries is the key to giving impetus to industrial transformation and upgrading, breathing new life into enterprises’ development[1]. Amid industrial digitization, the textile and clothing industry has faced several opportunities and challenges. Therefore, emphasis should be paid to optimizing production and increasing production efficiency[2]. As a cornerstone of digital transformation, industrial Internet integrates upstream and downstream enterprises and several factories having the same production capacity for real-time connection and intelligent interaction[3].

Manufacturing is a crucial component of the supply chain[4]; therefore, it is crucial to allocate the production orders according to factories’ indicators in the platform[5]. After obtaining a certain number of clothing task requirements from customers, the platform analyzes these requirements and allocates clothing orders to various factories in the platform, providing a corresponding processing capacity to complete the clothing tasks, which is known as the order allocation process. The balance and ratio of order arrangement involve the platform’s resource utilization and determine its economic benefits and market share[6]. Concerning large order quantities, working out reasonable and practical production schedules to ensure the timely accomplishment of production targets is a challenging problem currently being faced by the industrial Internet platform of textile and clothing.

In the industrial Internet platform of textile and clothing, customers provide orders, while the platform is responsible for organizing several factories to process the orders[7]. Multiple factories of different types complete the raw material processing for each sub-order. The platform, which currently relies on manual steps, allocates the clothing bulk orders. Therefore, it is challenging to meet the needs of production orders in such a platform having a relatively low efficiency. Recently, order allocation and supplier selection have drawn significant attention from scholars. Tsaietal.[8]proposed an ant colony system to examine the critical factors and their respective weights of different suppliers, and used them to grade these suppliers for determining the most appropriate ones. Scottetal.[9]applied a combined analytic hierarchy process(AHP) and a constrained optimization algorithm approach to design an integrated technique to help select suitable suppliers and allocate orders among them. Abdollahzadeh and Atashgar[10]put forward a multi-objective ant colony optimization algorithm; they dealt with uncertainties in supplier selection by applying maintenance threshold pheromone matrices, and redundancy-level pheromone matrices. Nazari-Shirkouhietal.[11]proposed an interactive two-phase fuzzy multi-objective linear programming model to minimize multiple objectives synchronously, including total costs, defective units, and late-delivered units. Liuetal.[12]examined the order allocation problem considering the similarity parameters of new orders within mass customization logistics services. However, the above methods primarily apply to supplier selection in the manufacturing industry, with comparatively limited research on order allocation in the industrial Internet.

With the vigorous development of the clothing e-commerce industry, clothing orders in e-commerce platforms exhibit a rapid growth trend[13]. Personalized clothing customization services provided by the industrial Internet platform of textile and clothing provide consumers with access to clothing details[14]. Therefore, the scale of consumer groups gathered by the industrial Internet will promptly increase, while order quantity will grow exponentially. Some achievements have been realized in order allocation; however, they mainly emphasize on the logistics supply chain and the traditional manufacturing industry, with inadequate studies on the textile and clothing industry.

This paper studies the optimization of order allocation in the production process of the industrial Internet platform of textile and clothing. We propose an order allocation model based on a genetic algorithm to achieve more adaptive production, improve the platform’s overall production efficiency, and stimulate the rationalization of platform allocation resources.

1 Order Allocation Modelling

The order allocation for multiple factories should ensure that the production of clothing orders meets the required quality and quantity.

1.1 Problem description

From the aspect of processing habits, the detachable basic clothing units are jackets and pants. Order allocation in the industrial Internet platform of textile and clothing relies on this premise. The specific problem is as follows: givenmorders andnfactories, the original order is disassembled, ensuring that the production task of the disassembled order contains only two kinds of products(i.e., jackets and pants), and a single factory or several different factories can process the sub-orders of each order. The processing time of each sub-order in different factories can vary considerably. The problem involves allocatingmorders tonfactories effectively and reasonably to ensure on-time delivery, and a load of factories in the platform can be balanced to attain a relatively optimal order allocation objective.

1.2 Order allocation model

According to the actual production requirements of the industrial Internet platform of textile and clothing, a mathematical model is proposed based on the following assumptions:

(1)Different factories can produce each product.

(2)Each factory has a certain production capacity limitation,i.e., the maximum production capacity while meeting the delivery time.

(3)All orders can be processed at the starting time.

(4)A factory can process only one production task at a certain time.

(5)During the plan’s implementation, the number of production factories on the platform remains unchanged, and no alternative factories are present.

Indices are as follows.

n: the total number of factories on the platform.

m: the total number of clothing orders received by the platform.

i:i-th factory in the platform;i=1, 2,…,n.

j:j-th order received by the platform;j=1, 2,…,m.

Decision variables are as follows.

yi: if thei-th candidate factory is selected, thenyi=1; otherwise,yi=0.

xij: if thei-th candidate factory takes charge ofj-th clothing order, thenxij=1; otherwise,xij=0.

aij: the number of clothing orders allocated by thei-th factory.

Parameters are as follows.

pij: the unit price of thej-th order in thei-th factory.

fi: the total fixed cost of thei-th factory.

bij: production capacity upper limit of thej-th order allocated by thei-th factory.

dij: delivery delay rate of thej-th order allocated by thei-th factory.

Li: minimum order quantities acceptable to thei-th candidate factory.

Ui: maximum order quantities acceptable to thei-th candidate factory.

In this appropriate order allocation problem, the objective function is to minimize total costsC, including product and fixed costs.

(1)

Model constraints:

bij≥aij,

(2)

aij≥0,yi=0 or 1,xij=0 or 1,

(3)

aij∈[Li,Ui],

(4)

(5)

Equation(2) ensures that the capacity load of a factory should be attainable, and for each product, a factory has an upper capacity limit in the stage. Equation(3) indicates the value range of each decision variable, or the non-negative constraint of production capacity and the binary variable constraint. Equation(4) ensures that the order quantity allocated to thei-th factory is acceptable. Equation(5) ensures that a certain proportion of products is delivered on time(on-time delivery rate is not less than 90%).

2 Model Solving Method

The order allocation problem is a combinatorial explosion problem[15], which is tough to solve by conventional mathematical programming methods. Accordingly, genetic algorithm(GA) can solve combinatorial optimization problems[16]; thus, it can solve the problem. Figure 1 provides the solution process using a flowchart of the design steps.

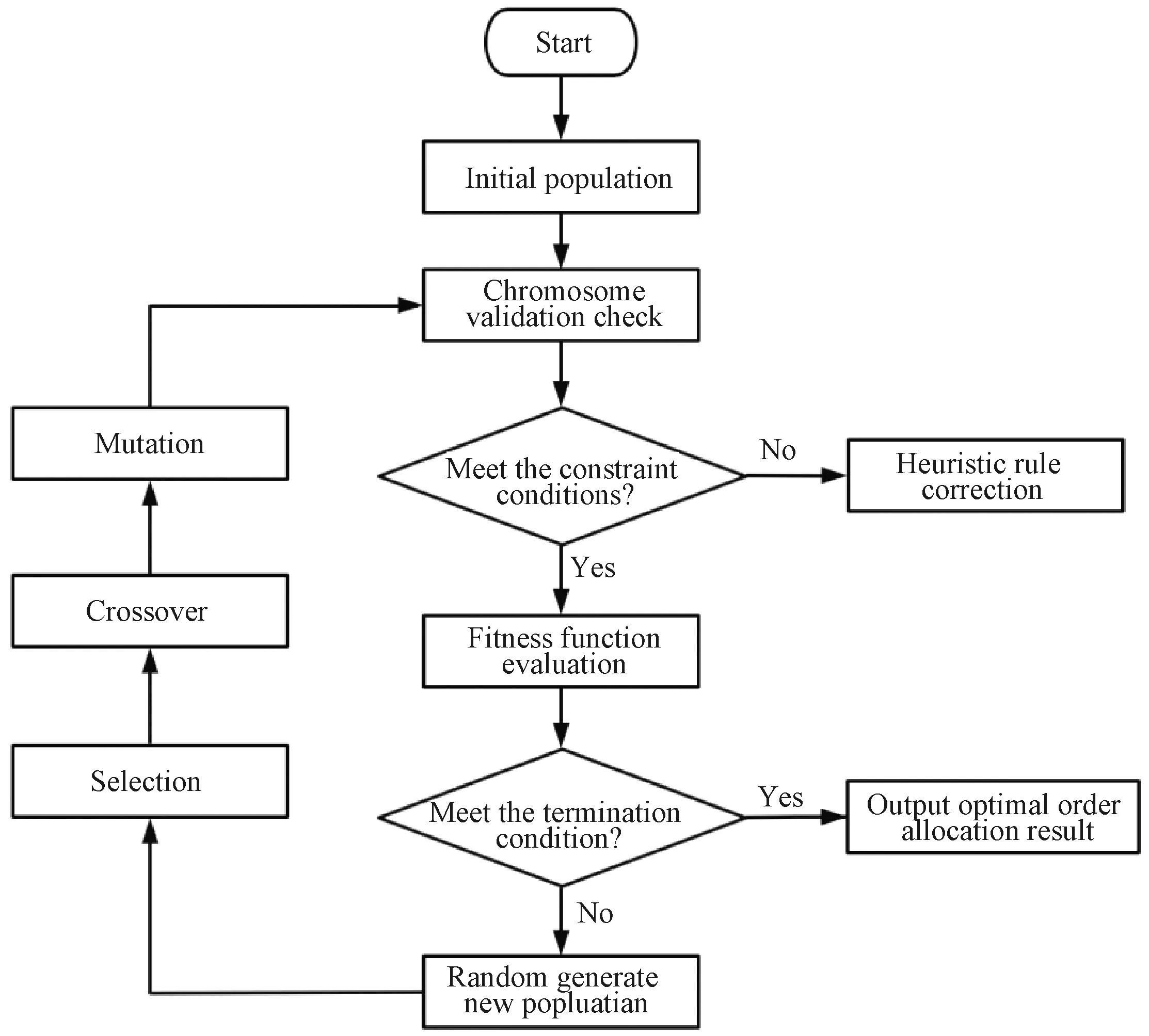
Fig. 1 GA flowchart

2.1 Chromosome coding and decoding

Coding is a crucial step when designing the GA since the decision variables in the model tend to influence each other. This paper encodes each chromosome by integer coding and provides a feasible order allocation scheme.

There arenfactories andmorders on the platform, and each order has two products. Each gene position corresponds ton-1 division points from 0 tom, and the orders are grouped intonintervals. After decoding, we can obtain the number of product orders assigned to each factory, and the chromosome length is 2(n-1).Girepresents the position of thei-th division point(i=1, 2,…,n-1).G=[G1,G2, …,Gi, …,Gn-1] represents a chromosome. By decoding the chromosomes, the corresponding order quantities assigned to each factory are [G1,G2-G1, …,Gi-Gi-1, …,m-Gn-1]. Figures 2 and 3 present an example of chromosome coding and decoding, and the two products are represented by green and yellow, respectively.

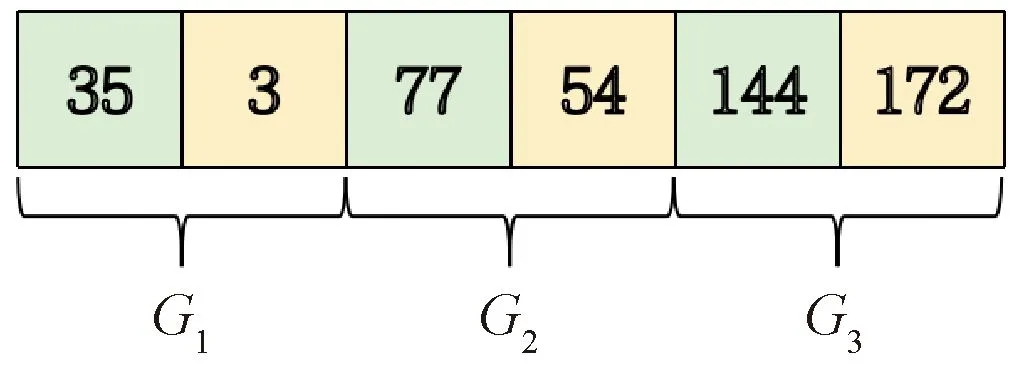
Fig. 2 An example of chromosome coding

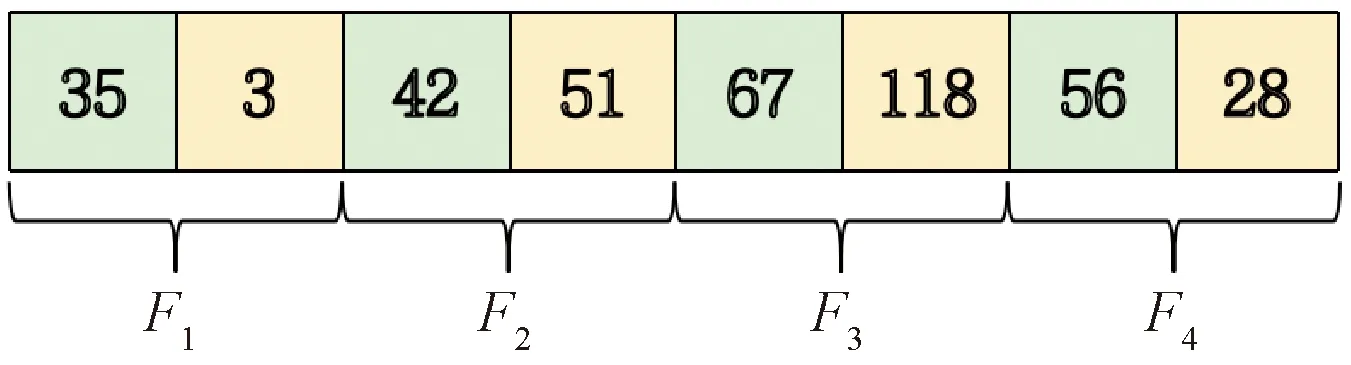
Fig. 3 Number of orders for each factory after decoding

Given multiple constraints in the model, invalid chromosomes that violate the constraints may arise after genetic operators operate the legal parent chromosomes. According to the characteristics of the objective function in the model, we select the penalty strategy to deal with invalid chromosomes. Specifically, a penalty term is added to the objective function, thus reducing the individual fitness value of illegal constraints.

2.2 Fitness function

Fitness function is an evaluation function for assessing whether the chromosomes are transmitted to subsequent generations. It can represent the fitness value of each chromosome and depict how much the solution is fitted. In this problem, we should identify the global minimum of the objective function according to Eq.(1) of the algorithm model. The fitness valueF(x) is designed in Eq.(6), whereC(x) is the objective function value of an individual, andZmaxis the maximum objective function value in the evolution process.

(6)

2.3 Crossover operation

The crossover operator is an essential process of GA, and it is conducive to spreading excellent genes or gene fragments. This operator selects two arbitrary combination points for both parents’ chromosomes according to the crossover probabilityPc. Moreover, the gene sequence in two points remains unchanged during the crossover process. The chromosomic sections after these combination points are swapped with each other, giving birth to two new offspring.

2.4 Mutation operation

The mutation operation applies to each individual after the crossover operation, which is vital to maintain genetic diversity from one generation to the next. We apply substitution mutation to select a gene position on the chromosome randomly, and then generate a non-negative integer that is not more significant than the maximum production capacity of the corresponding factory after decoding at the division point through the mutation probabilityPm. We replace the original gene at the position.

2.5 Selection operation

To avoid premature convergence, the selection operator can keep the chromosome of larger fitness down to the next generation. In this paper, the roulette wheel is adopted for selection operation since it is extensively used for chromosome selection[17]to accelerate the algorithm’s convergence.

Assuming that the population size isn, the selection probabilityPiof thei-th individual is expressed in Eq.(7), whereFiis the fitness value ofi-th chromosome.

(7)

2.6 Termination condition

When the number of iterations exceeds a given value, the algorithm stops running. The optimal solution obtained at this instance is the relatively optimal order allocation scheme required by the industrial Internet platform for textile and clothing.

3 Experimental Verification and Result Analysis

We take an actual order situation from an industrial Internet platform for textile and clothing as an example. After analysis, the actual orders and the factory information in the platform are selected for experimental verification. We assume that the ordered products are a batch of suits, including suit jackets and suit pants. There are four factories on the platform and 200 orders for allocation. Table 1 presents the suit price, fixed cost, maximum production capacity, and delivery delay rate for each factory.

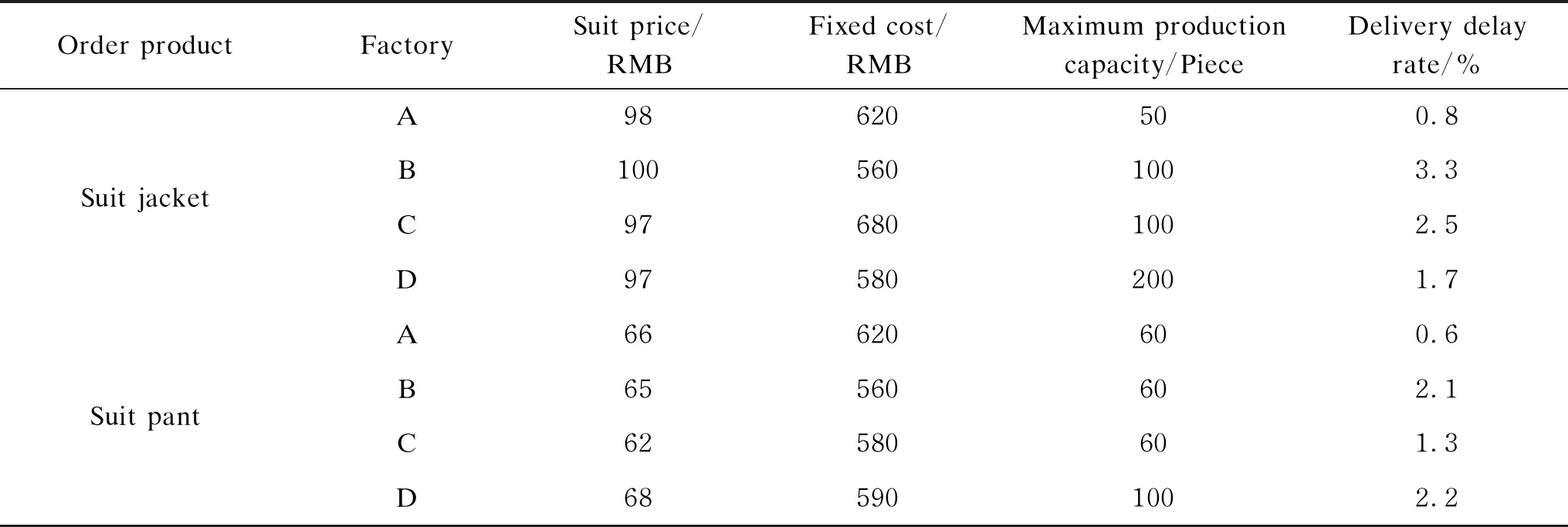
Table 1 Factory’s details

The program is written in Python 3.7 software and runs on a computer using Windows 10 with a 3.00 GHz (R) Core(TM) processor and 16 GB memory. Through several pre-experiments, the general parameter values in the GA are adjusted, and ultimately determined as follows: the initial population size is 1 000, the crossover probability is 0.7, the mutation probability is 0.01, and the number of iterations is 150.

Figure 4 illustrates the change in fitness value in this problem. With an increase in the number of generations, the feasible solutions go towards optimal ones. The optimal value of a generation number is 67, against the fitness value of 1 589.32. Table 2 presents the calculated order task assignment results. The total optimization cost is 36 108 RMB, and the running time is 15.7 s. Compared to the original order allocation based on experience, the new order allocation has several optimization effects.

Fig. 4 Fitness in different generations

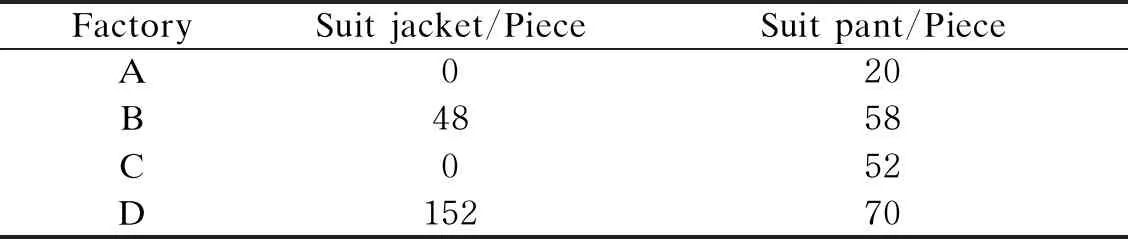
Table 2 Order allocation results

To verify the algorithm’s effectiveness, Table 3 lists the comparison results of the different methods for the above factory examples. Based on the experience of traditional manual allocation, most suit orders are typically assigned to relatively low-cost factories without exceeding their maximum production capacity, and the corresponding value is 36 950 RMB. If the suit orders are evenly assigned to each factory, the total cost becomes 37 440 RMB. From the comparison results in Table 3, the objective function can be optimized respectively by 2.28% and 3.56% by GA, and the running time is much shorter than that of the other two methods. It proves that the order allocation algorithm and the model used in this paper can optimize the order allocation of the industrial Internet platform for textile and clothing and enhance its resource utilization.

Table 3 Comparison results of different methods

4 Conclusions

In the era of digital transformation, the order allocation problem has been facing a vital informatization challenge. Based on the industrial Internet platform for textile and clothing, we model the manufacturing capability of all enterprises in the platform. From the experimental results, the GA proposed in this paper has a simple gene coding and a fast convergence speed. Therefore, it can solve the order allocation problem under the constraint of platform resources. It has a good applicability in actual production scheduling and can provide an order allocation scheme that guides actual production tasks effectively in the industrial Internet platform for textile and clothing. This method can reduce platform cost and on-time delivery ratio, and enhance customer satisfaction.