具有外部干扰的离散时间多智能体系统包含控制
刘东南,李博凡,李 玲
(1.湖南工业大学 理学院,湖南 株洲 412007;2.湖南铁路科技职业技术学院 铁道供电与电气学院,湖南 株洲 412006)
1 研究背景
近年来,高阶离散时间多智能体系统(multi-agent systems,MAS)的分布式协同控制引起了学者们的广泛关注。一致性是分布式协同控制问题中的一个基础问题,即使智能体间达成一种共同状态。学者们在同步、群集、编队等方面,关于一致性的研究成果[1-6]较多。
根据领导者的数量,一致性可以分为无领导者一致性、跟随领导者一致性和包含控制。所谓包含控制是指网络中所有跟随者渐近进入到网络中的多个领导者所形成的凸包之中。由于包含控制在许多领域都具有良好的应用前景,受到了许多学者们的关注。Cao Y.C.等[7]研究了在不同拓扑下具有多个静态或动态领导者的MAS的分布式包含控制。Liu H.Y.等[8]通过连续控制和采样控制,分别研究了MAS 的包含控制,并得到了包含达到的充要条件。Li Z.K.等[9]在有向拓扑的条件下,研究了一般线性MAS的干扰抑制问题,提出了状态反馈协议和基于观测器的协议。M.Asgari等[10]考虑了在有向拓扑下具有固定时间延迟的异构MAS的包含性。Liu H.Y.等[11]研究了基于采样数据的分数阶MAS包含控制。Wang Y.W.等[12]通过脉冲控制,研究了异源多智能体系统的输出编队包含性问题。
此外,在近年内,关于离散时间MAS的包含控制问题,学者们也进行了大量研究,取得了较多的成果。Ma Q.等[13]研究了离散时间MAS的包含控制问题,并在所提出的协议下得到了低保守的充要条件。Wang D.等[14]利用z变换研究了具有时滞的离散时间MAS的包含性。Zhao Z.Y.等[15]研究了具有执行器位置和速率饱和的离散时间MAS的半全局包含控制。
干扰常常存在于各类系统中,是系统不稳定的重要因素。因此,研究具有干扰的多智能体系统协调控制具有重要意义,对具有外部干扰的多智能体系统的研究尤为重要。Guo L.等[16]提出了基于干扰观测器(disturbance observer,DO)的控制方法,以稳定具有外部干扰的非线性系统。Yang H.Y.等[17]提出了求解具有外部干扰的二阶MAS的一致性问题的方法。Xu C.J.等[18]利用DO技术研究了具有外部干扰的连续时间MAS的包含控制问题。
目前,已有的包含控制研究主要是针对连续时间多智能体系统的。在上述文献的启发下,本文研究具有外部干扰的离散时间线性MAS的包含控制。
2 模型介绍和预备知识
设图G=(V,E,A)表示一个网络拓扑,它包括一组节点V={1, 2, …,N+M},一组边EV×V,以及相邻矩阵A=[aij]。对于有向图,aij>0(j,i)∈E,即j向i发送信息;对于无向图,aij>0,即j不仅向i发送信息,而且还接收来自i的信息。Ni={j|(j,i)∈E}是第i个节点的邻居集。
L=D-A=[lij]是拉普拉斯矩阵,式中D=,所以lii=,lij=-aij(i≠j)。
设∑1={1, 2, …,N}和∑2={N+1,N+2, …,N+M}分别为追随者和领导者集合,即追随者和领导者的编号分别记为1, 2, …,N和N+1,N+2, …,N+M。追随者之间的网络拓扑是无向的,领导者和每个追随者之间的拓扑是有向的。因此,L可以重写为
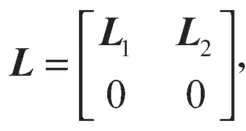
式中:L1为跟随者所对应的Laplacian矩阵子块;
L2为跟随者与领导者间邻接关系所对应的Laplacian矩阵子块。
第i个跟随者的动力学方程描述为

第i个领导者的动力学方程描述为

式(1)~(2)中:xi、ui、di分别为第i个智能体的状态、控制输入、外部干扰,且xi∈Rn、ui∈Rm、di∈Rm;
A、B都为常数矩阵,且A∈Rn×n、B∈Rn×m。
设干扰ωi(t)(i= 1, 2, …, N)由外部系统(3)所生成,

式中:ωi为外部系统的状态,且ωi∈Rl;
S、F都为干扰系统的矩阵,且S∈Rl×l,F∈Rm×l。
定义1[18]设C是Rn的子集,如果C中的任何x和y以及任何α∈[0,1],满足(1-α)x+αy∈C,则集合C称为凸集。一个点集X={x1,x2, …,xn}的凸包是指包含X中所有点的最小凸集,X的凸包记为Co(X)。
假设1假设追随者之间的连边是无向的,对于每个跟随者,至少有一个领导者有指向该跟随者的定向路径。
假设2假设矩阵对(A,B)是稳定的。
引理1[18]若假设2成立,则存在唯一的正定矩阵P,满足改进的代数里卡提(Ricatti)方程
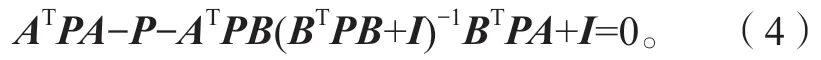
引理2[14]若假设1成立,则L1是正定的,矩阵-L1-1L2中的每一项都是非负的,且矩阵每一行的和都为1。
3 基于干扰观测器的状态反馈包含控制
本章先提出基于干扰观测器(DO)的分布式状态反馈包含控制协议,然后给出包含达到的条件。
依赖于状态的离散时间干扰观测器为
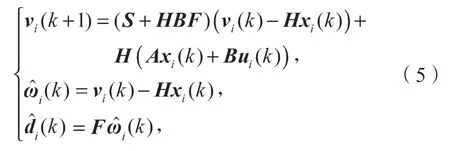
式中:vi为观测器的内部状态变量,vi∈Rl;
H为观测器的增益矩阵,H∈Rl×n。
注1由于网络中的智能体无法获得干扰的信息,智能体必须估计外部干扰的值。
由式(5)构造离散干扰观测器来估计干扰。
根据式(1)和式(5),有

定义δi=ωi-,由式(3)和式(5),得
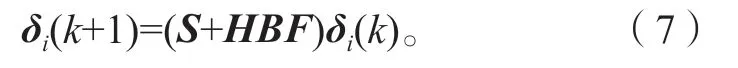
基于分布式DO的状态反馈包含控制协议构造如下:
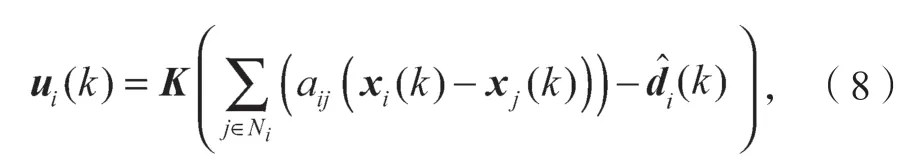
式中K是要设计的增益。
注2包含协议由两部分构成,即包含协议依赖于ωi的估计值和局部相关信息。
令

则

定理1若假设1和假设2成立,在基于离散时间DO状态反馈包含协议(8)下,
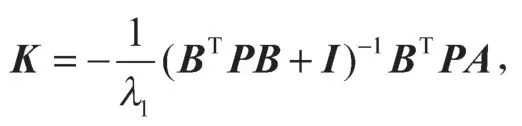
P>0是代数里卡提方程(4)的唯一解,λ1是L1的最小特征值;S+HBF是舒尔(Schur)稳定的。则系统(1)可以实现包含控制,而且
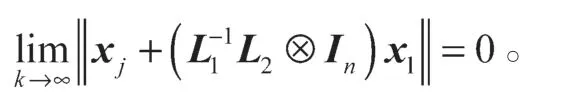
证明令
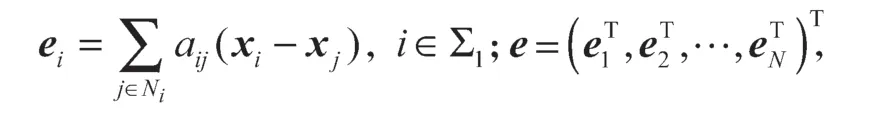
根据L的定义,有
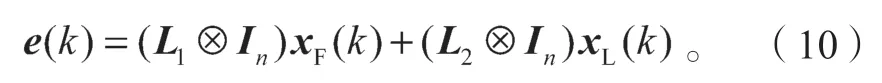
根据式(9)和式(10),有

因此,误差系统可以改写为
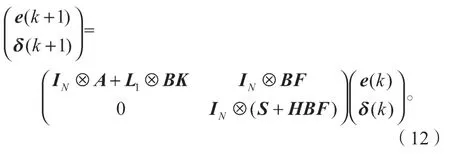
根据引理2,若假设1成立,则L1是正定且非奇异的,从而得λi>0(i=1, 2, …,N)。
对于离散时间系统x(k+1)=(A+λ1BK)x(k),,选择离散时间李雅普诺夫函数为V(k)=xT(k)Px(k),其中P是改进的离散时间代数里卡提方程的唯一解,则有
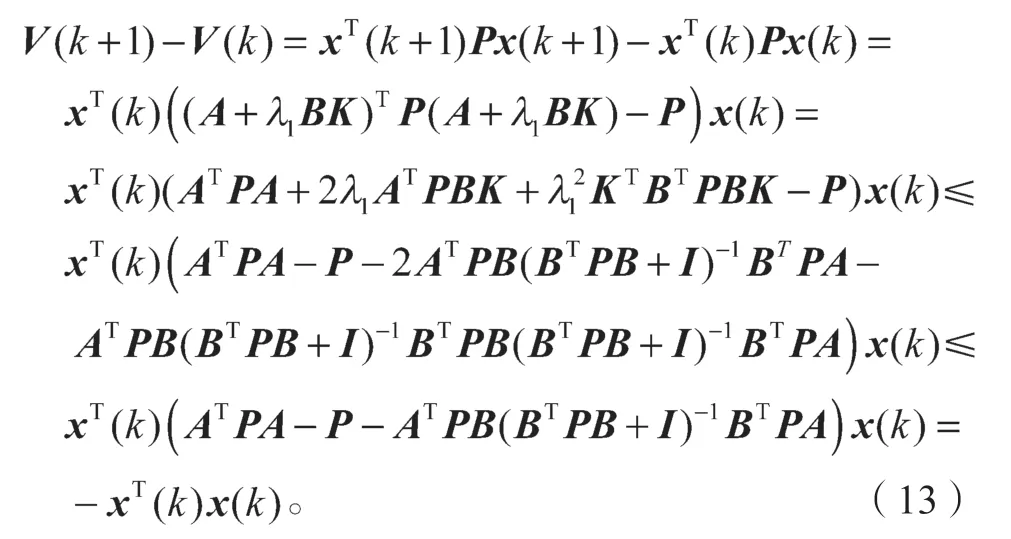
当k→∞时,V(k)→0,因此A+λ1BK是Schur稳定的。于是可以得出结论:对于i=2, 3, …,N,A+λiBK是Schur稳定的。从而得到INA+L1BK是Schur稳定的。
另一方面,S+HBF是Schur稳定的,因此INA+L1BK和S+HBF都是Schur稳定的,从而误差系统(12)为Schur稳定的。
当t→∞时,δ(k)→0,e(k)→0,则xF→根据引理2,-L1-1L2每一行的和等于1。再由定义1知,-(L1-1L2In)xL在由领导者和干扰观测器渐近收敛于0的误差所张成的凸包里,所以定理1成立。
注3当di(k)=0时,不妨设F=0,此时=0。包含控制协议(8)依已有多智能体系统(4)达到包含,相关结果见式(13),系统(1)~(2)具有如下形式:

注4当领导者个数为1时,包含控制问题转化为一般性问题,系统(1)~(2)具有如下形式:
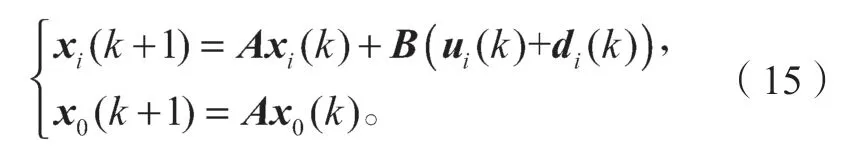
此时假设1退化为全局可达。相应地,由定理1及其证明可得如下推论1。
推论1在假设1和假设2成立的条件下,多智能体系统(15),在干扰观测器(5)的作用下可达到一致。
4 数值仿真
本章通过数值模拟来验证前述理论的正确性。
设多智能体系统由6个追随者和3个领导者组成,其拓扑结构如图1所示。
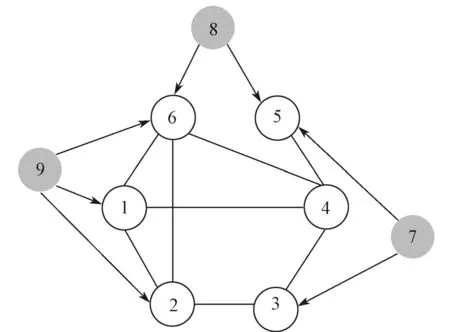
图1 多智能体系统的拓扑结构图Fig.1 Topological graph of the multi-agent system
选择系统矩阵A、B、C、D、F和S如下:

从而可得以下动态方程:
若i∈F,

若i∈L,

易证(A,B)是稳定的。S的特征值为1.030 3和0.669 7,这表明S不是Schur稳定的。
选择增益矩阵

则A+DC的特征值为-0.988 1和0.198 1,S+HBF的特征值为0.997 3和0.708 7,从而A+DC和S+HBF都是Schur稳定的,因此满足定理1的条件。根据Ricatti代数方程(4),有如下正定矩阵:
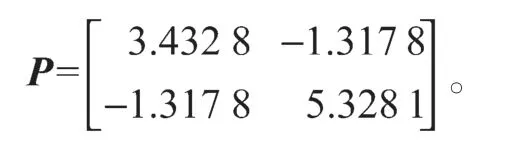
矩阵P的最大特征值λmax(P)=6.003 6,根据拉普拉斯矩阵,可得λ1=1.615 3,可以获得相应的控制器(8),其中

对应的领导者和跟随者的运动轨迹仿真结果如图2所示。

图2 基于DO的状态反馈包含控制仿真结果图Fig.2 DO-based simulation diagram of state feedback containment control
由图2可知,所有追随者都聚集在由领导者所张成的凸包内。
5 结语
本文研究了具有外部干扰的离散时间高阶MAS的包含控制,利用基于对状态信息的干扰观测器,提出了相应的包含控制协议,不仅有效抑制了干扰,同时还能使系统达到包含。利用李雅普诺夫方法对系统的稳定性进行分析,得到了包含达到的充分条件。最后通过数值模拟验证了理论结果的正确性。
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

