胶合木张弦梁结构施工阶段监测研究
潘 鸿 黄俊杰 刘得龙 孙 赫 张 晋
(1.中亿丰建设集团股份有限公司 江苏苏州 215131;2.东南大学 混凝土及预应力混凝土结构教育部重点实验室 江苏南京 211189)
0 引言
预应力张弦结构,是斋藤公男于1979年提出的一种现代张弦结构。由于造型优美、施工简便、受力性能良好等优点,如今已在体育、会展、交通设施等大型公共建筑中得到广泛的应用[1]。以往建造的张弦结构多是钢结构体系,例如广州国际会展中心、上海虹桥机场[2],以木材为主体的张弦结构较少。随着人们对建筑美观、节能方面的要求越来越高,而木结构以美观、节能著称,所以木结构为主体的张弦结构将会越来越流行。
根据以往张弦钢结构的建造经验可知:张弦结构在施工过程中会产生较大变形、材料的材性受环境因素影响大、构件往往存在初始缺陷。因此,结构实际状态与分析模型存在差异。为保障结构在施工阶段的位移、应变和索力符合设计预期,对使用阶段出现的危险情况能及时预警、评估,确保结构的安全运营[3],往往会对结构进行健康监测。木材的材性相对钢材更为复杂,同时由于张弦结构兴起较晚,国内在张弦钢结构的健康监测方面的文献相对较少[4],张弦木结构健康监测的相关文献更是寥寥无几。所以,对胶合木张弦梁结构进行健康监测,探索实际结构与计算模型存在的差异,是亟待解决的问题。
本文以苏州第二工人文化宫游泳馆胶合木张弦梁结构施工阶段的监测为例,提供了张弦梁结构位移、应力、索力在施工阶段监测的结果,并对监测结果进行简要分析;将数值模型的计算结果与实际监测结果对比,论证了模型的有效性,为以后相关的工程实践提供参考。
1 工程概况
苏州第二工人文化宫位于苏州市相城区,由9个建筑结构单体组成,其中的游泳馆纵向跨度67.2 m,横向跨度36.6 m,占地面积2460 m2,内设游泳池、戏水池和看台。游泳馆屋面采用坡屋面形式,屋盖采用张弦梁结构,如图1所示。主次梁采用TCT21胶合木,主梁截面为210 mm×800 mm,次梁截面为170 mm×400 mm、130 mm×300 mm和210 mm×500 mm,预应力索采用锌-5%铝-混合稀土合金镀层钢索。

图1 胶合木张弦梁结构
2 监测准备
2.1 结构施工阶段划分
张弦结构在施工过程中受力状态是变化的,是一个极其复杂的状态,因此划分施工阶段十分必要。根据以往的经验,施工阶段大致可以分为安装阶段、张拉阶段、附属体系施工阶段,对应结构的3种受力状态:零状态、初始态和荷载态[5]。
本文中胶合木张弦梁结构3个施工阶段的任务如下:
(1)满堂脚手高空拼装,木梁安装就位,拉索安装与预紧。此时木梁搁置在满堂脚手架上,结构处于零状态——无任何预应力与外荷载作用。
(2)按顺序对张弦木梁进行张拉。为保证结构在张拉过程中的可控性,本工程的拉索采用分阶段张拉,每一阶段张拉时,由15轴向23轴(图2)依次逐榀张拉,交叉两根拉索同时张拉。

(●为应力测点,▲为位移测点,△为索力测点)图2 结构平面及测点布置图
张拉第一阶段:按顺序张拉到90%设计工况对应索力。一根拉索有两个张拉调节端,对于同时实施张拉的两根拉索,共4个张拉调节端。考虑到4个张拉端同时张拉,对本阶段的90%设计工况对应索力进行分级张拉:预紧→27%→54%→81%→90%。
张拉第二阶段:按顺序张拉到100%设计工况对应索力。张拉完成的张弦木结构处于初始态-预应力和自重共同作用。
(3)进行屋面、幕墙等其他附属体系的施工,施工完成后结构投入使用。此时为结构的荷载态——结构受到预应力、自重和其他外荷载的作用。
2.2 结构监测阶段划分
本工程中,监测阶段的划分主要依据《建筑施工测量标准》(JGJ/T 408-2017)[6]13.5.5小节相关要求、《建筑与桥梁结构监测技术规范》(GB50982-2014)[7]中相关要求和木结构施工阶段划分,拟定以下施工监测阶段,如表1所示。
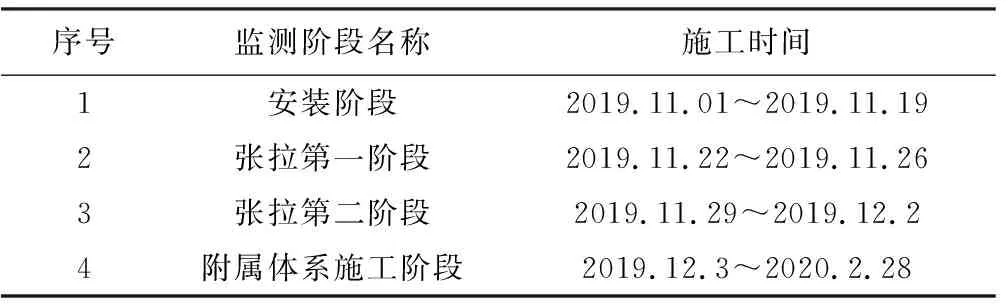
表1 施工监测阶段划分
2.3 测点布置
查阅相关文献可知,木结构建筑往往以最大位移作为结构安全的控制指标,索力是以往张弦钢结构监测的重要参数[8]。因此,本工程的健康监测以位移为主控参数,索力为第二控制参数,并综合考虑构件的应力,来判断结构的安全性。所以,本工程的监测内容为撑杆的竖向位移、拉索的索力和木梁控制截面的应力。
位移监测依照《建筑变形测量规范》(JGJ8-2016)[9]中4.5节相关要求,采用电子全站仪对测点的竖向位移定期进行测量。该工程通过在撑杆上粘贴反射片的方式,共设8个测点,编号依次为W-1~8,安装位置如图2所示。
索力监测采用在拉索上安装EM磁通量索力传感器的方式,进行长期观测,共设8个测点,编号依次为S-1~8,测点位置如图2所示。
应力监测采用在木梁上安装BGK-4000振弦式应变计的方式,对应力进行长期观测,选取8处木梁截面为测点,编号依次为YL-1~8,测点位置;每处测点安装3个振弦式应变传感器,3个传感器分别用螺钉固定在木梁侧面距顶部5 cm、木梁侧面中间和木梁底面中间。
2.4 MIDAS计算模型
(1)计算模型
该工程采用有限元分析软件Midas Gen进行分析,木梁采用梁单元进行模拟,撑杆采用桁架单元模拟,拉索采用只受拉索单元进行模拟。TCT21胶合木材:弹性模量为8000 MPa,泊松比为0.37,线膨胀系数为1.2×10-6,重量密度为5.00×10-6N/mm3;预应力钢丝的弹性模量取1.6×105MPa,泊松比为0.3,温度膨胀系数为1.2×10-5,重量密度为7.698×10-5N/mm3。使用Midas Gen软件所建立的模型如图3所示。

图3 结构计算模型
(2)荷载及边界条件
木结构屋盖恒载根据建筑屋面常规做法取1.5 kN/m2;活载按不上人屋面荷载取0.7 kN/m2;按《建筑结构荷载规范》(GB50009-2012)[10]基本雪压取0.40 kN/m2。考虑到木结构建筑对风荷载的敏感性,基本风压取0.40 kN/m2。
图2中标注了各种节点的类型,其中主次梁节点S1、S2所用连接多、刚度大,如图4所示,在模型中按半刚性节点考虑。因此,将节点S1、S2的X、Y、Z向位移和沿X、Z轴的转动固定,将Y轴的转动刚度设为6210 kN·m/rad。节点S3、S4和S5按铰接节点建模。
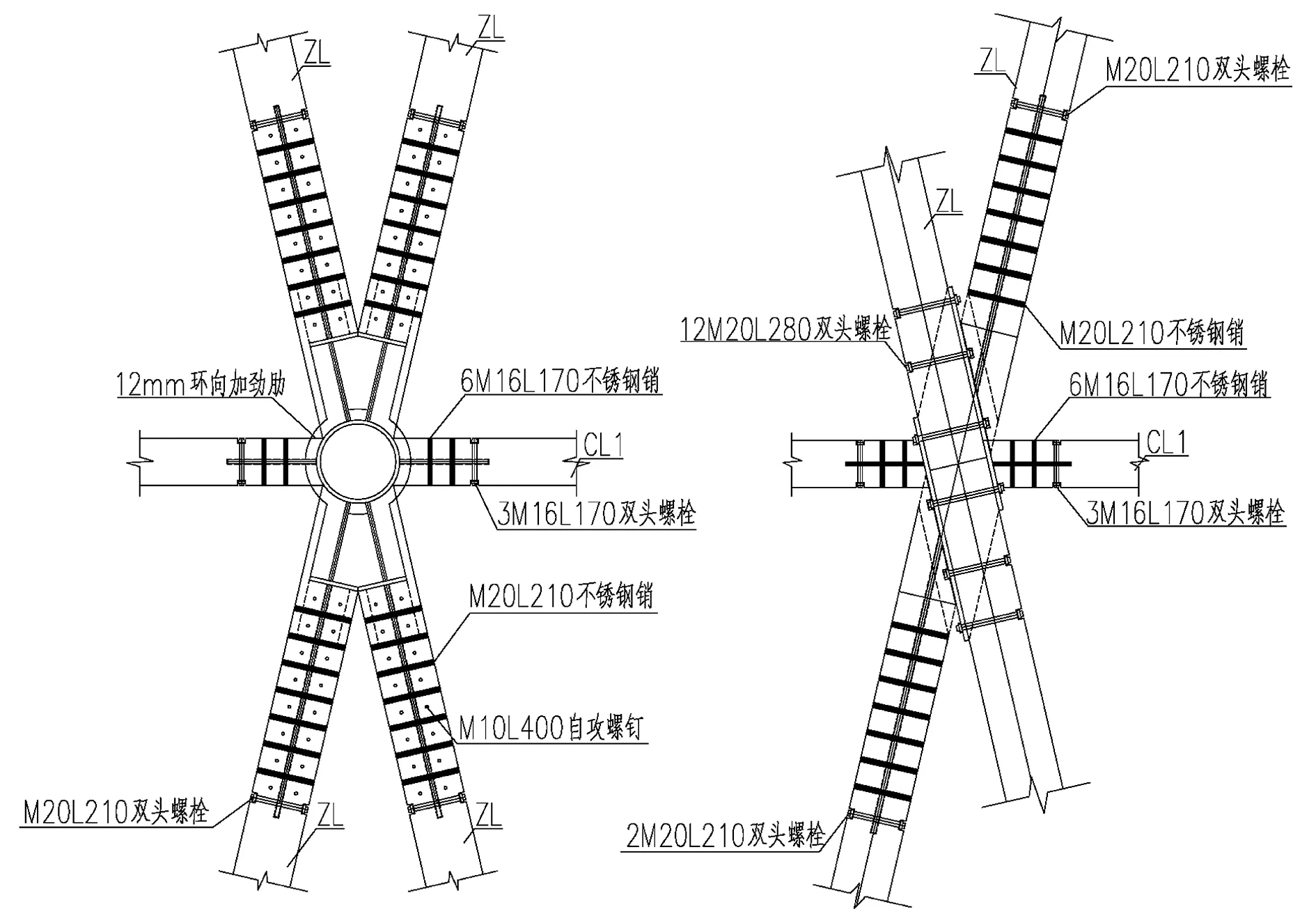
图4 S1(左)、S2(右)节点详图
3 监测结果分析
本工程中,测点位移数据为测点。相对于零状态下初始标高的变化值,测点上移为“+”,反之为“-”,单位取mm;应力为应变与TCT21胶合木弹性模量的乘积,单位取MPa;索力单位取kN。
3.1 温度对监测结果的影响
图5给出测点YL-1的应力、温度变化图,图6为测点S-2的索力、温度变化图。
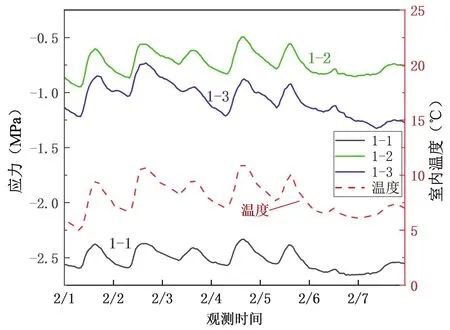
图5 测点YL-1应力、室内温度变化图
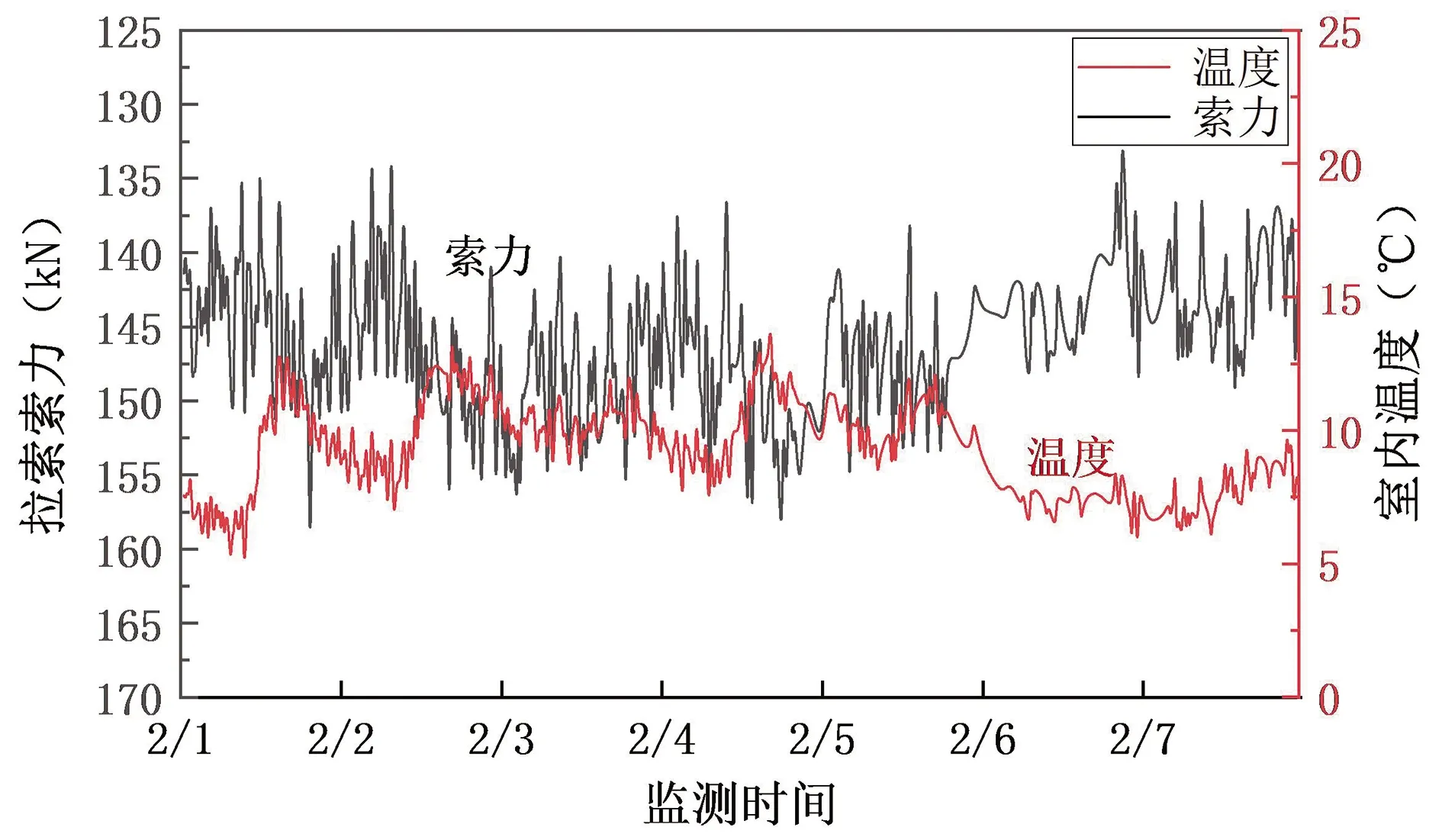
图6 测点S-2索力、室内温度变化图
从图5可以看出,测点的应力值和温度的变化趋势一致,都以一天为周期变化。正午温度最高,应力值最小;夜间温度最低,相应的应力值最大。从图6可以看出,测点的索力值和温度亦存在相关性,索力随温度近似以一天为周期变化,温度升高,拉索松弛索力减小,温度降低,拉索收紧索力增加。
环境温度的变化会影响结构的响应,从而使监测数据发生波动。由图5和图6可知,应力和索力都与温度存在较强的相关性。因此在选取监测值时,以天为单位,取每天监测的应力、索力、温度平均值作为监测值,同时在计算模型中,也将考虑环境温度变化带来的影响。
3.2 计算值与监测值比较
由图7~图10可知,屋盖结构张拉第二阶段完成后的测点位移,附属体系施工完成后测点的位移、索力和应力计算值与实测值均相差较大。理论模型不能对现场实际结构进行很好的模拟,需要对模型进行修改。

图7 张拉第二阶段完成后W-1~8位移
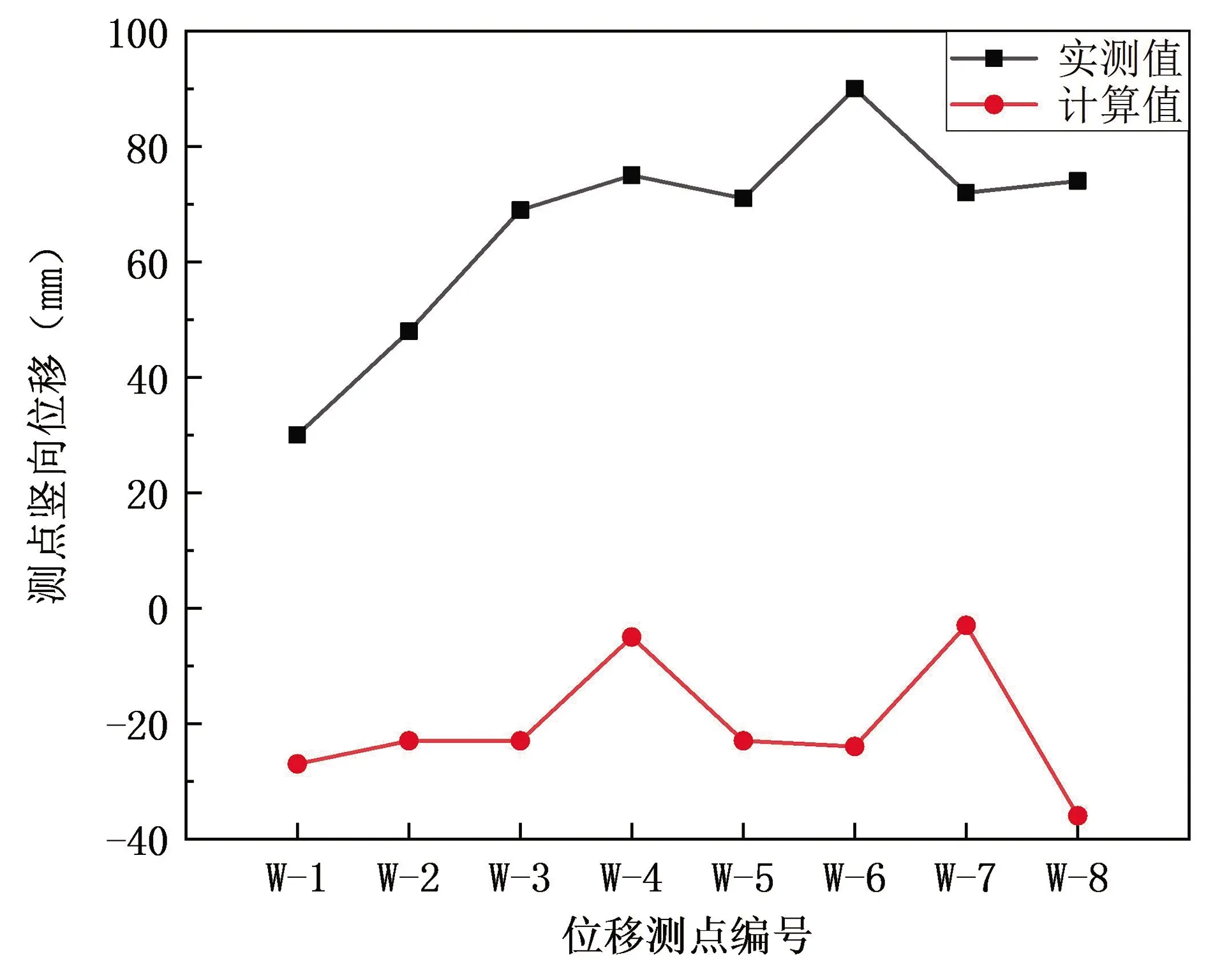
图8 附属体系施工完成后W-1~8位移
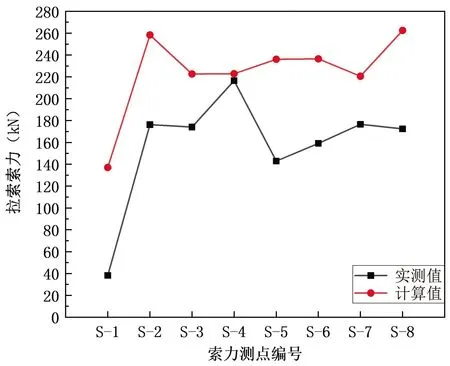
图9 附属体系施工完成后S-1~8索力
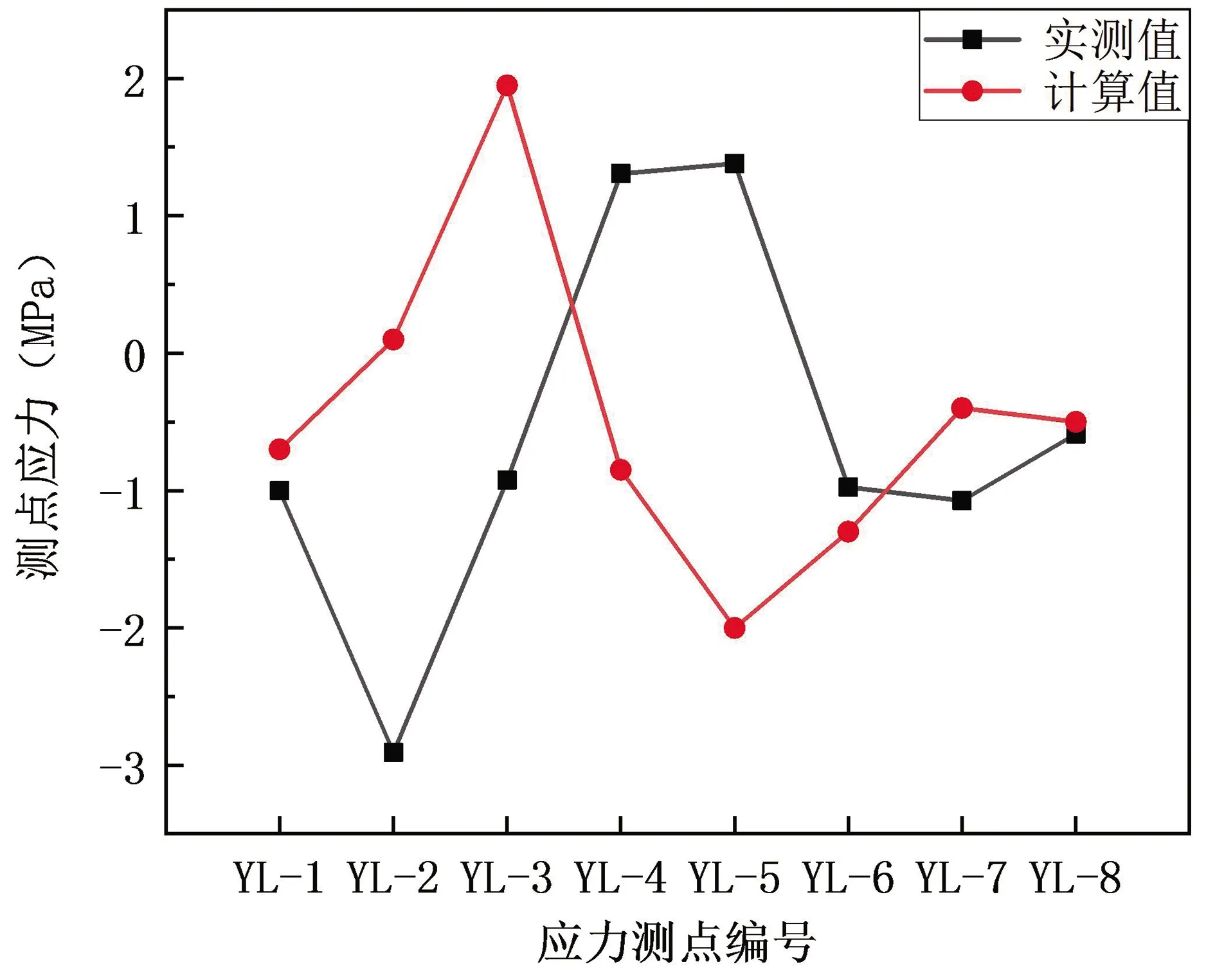
图10 附属体系施工完成后YL-1~8应力
3.3 模型修正
由3.2节可知,计算模型不能很好地模拟现场实际情况,建立的模型可能和实际结构存在差异。因此,需要对模型的参数进行修改。
结构刚度修正:从图7中可以看出,在张拉第二阶段完成后,测点的反拱位移实测值均大于计算值。由此可看出,实际屋盖结构沿竖向刚度偏小,结构偏柔。因此,需减小模型沿竖向的转动刚度,使模型与实际结构相符。由于本模型中半刚性节点S1、S2沿Y轴的转动刚度(SRy)设置不合理,故在控制恒载下拉索索力值基本不变的情况下,将原计算模型中拼接节点的转动刚度减小(由6210kN·m/rad减小至500kN·m/rad)。
屋面荷载修正:附属体系施工阶段完成后的计算模型的位移、索力和应力,均和实际结构存在较大差异。经梳理对比,查明造成上述偏差的原因为:计算模型中的屋面恒载是根据屋面建筑常规做法,取值为1.5kN/m2;而本工程在详图设计阶段对屋面结构进行了设计优化,优化后的屋面恒载约为0.7kN/m2。
3.4 修正后计算值与监测值比较
将计算模型修正后,重新计算结构的位移、拉索索力和梁截面应力,并将计算结果与实测值进行比较。
3.4.1 位移对比
模型修正后的位移实测值与计算值对比如图11~图12所示。由图11可知,张拉第二阶段完成后,测点位移计算值对实测值的模拟效果有了明显改善,计算值与实测值更加接近。但由图12可知,附属体系施工阶段完成后的位移计算值与实测值依然存在较大误差,原因可能是第二和第三施工阶段的累计误差和模型与实际存在系统误差。为此,在图13中分析了附属体系施工阶段内的位移(“附属体系施工阶段完成的位移”-“张拉第二阶段完成的位移”)以验证模型的有效性。

图11 (模型修正后)张拉第二阶段完成后W1~8位移

图12 (模型修正后)附属体系施工完成后W1~8位移
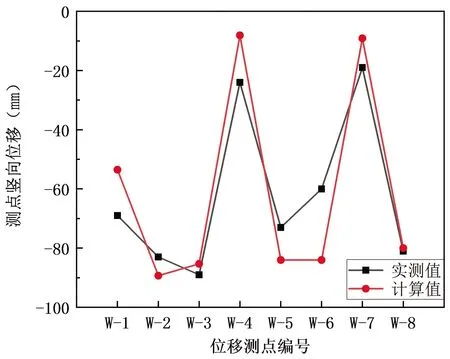
图13 (模型修正后)附属体系施工阶段内W-1~8位移
由图13给出的位移结果可以看出,附属体系施工阶段内的位移实测值和计算值两者吻合很好、误差很小,说明使用该计算模型进行屋面结构位移分析是可靠的。
3.4.2 索力对比
模型修正后的索力实测值与计算值对比,如图14所示。
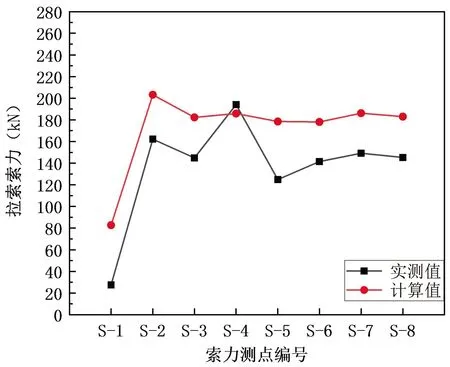
图14 (模型修正后)附属体系施工完成后S-1~8索力
对比索力计算值曲线与实测值曲线可知,索力的计算值曲线与实测值曲线近似平行。除了测点S-4外,其余测点的索力计算值与实测值相差都在30 kN~60 kN之间。因此,计算模型和实际测量结果可能存在系统误差。但是计算模型也可以用来反映实际工程结果。
3.4.3 应力对比
图15给出了附属体系施工完成后的应力实测值与计算值对比。由图15可看出,在模型修正后,各测点的应力计算值对实测值的模拟效果较好,计算模型可以较好地反映现场实际结构。

图15 (模型修正后)附属体系施工完成后YB-1~8应力
4 结论
本文对苏州第二文化宫游泳馆施工阶段进行了系统的监测。通过对结构施工过程中位移、应力及索力监测,对有限元模型的数值模拟,结合监测数据、计算数据的采集汇总分析,得到以下结论:
(1)基于相关规范与拉索的施工阶段划分的施工监测阶段,可以较好反映胶合木张弦梁结构的位移、索力和应力在整个施工过程中动态变化,监测方案合理可行。
(2)胶合木张弦梁结构的监测结果均受环境温度的影响。其中木梁应变、拉索索力随环境温度变化而发生一致的变化,以天为周期,波动范围较大,受环境温度影响较明显。
(3)建立张弦木结构建筑模型时,应合理设置节点刚度(必要时可进行相关节点试验),严格把控节点的施工质量,以使计算模型与实际工程更加契合,使模拟更真实有效。
(4)张弦梁木屋盖在施工过程中,采集到的数据与修正后的计算模型的结果基本相符,偏差在较合理的范围内,验证了计算模型的合理性和正确性,计算结果可以为结构提供预警、评估。

