基于三参数区间泛灰数的技术站能力表示与估计方法

薛 锋，袁 野，户佐安，白 瑞

（1.西南交通大学交通运输与物流学院，四川 成都 611756；2.西南交通大学综合交通运输智能化国家地方联合工程实验室，四川 成都 611756；3.西南交通大学综合交通大数据应用技术国家工程实验室，四川 成都 611756；4.雄安城市规划设计研究院绿色交通设计研究所，河北 雄安 071700）

技术站能力是实现作业资源分配的重要依据，由于其计算方法和测定手段的多样性，能力的计算结果与作业实绩有时相差较大，导致能力在运用中呈现“膨胀”或“萎缩”现象.而且，技术站列车的实际到发时间、技术作业时间等并非固定，这使得能力的测定结果存在一定的波动性，但这种波动并不是完全随机的而是在一定范围内呈现特定规律的波动.原有的能力单一定值表示方法虽然简洁直观，但并未体现能力的动态性特征.

国内外学者从不同角度对技术站能力做过较多研究：刘澜等[1]给出了一种咽喉通过能力的计算方法，提出以同构网络上的最小费用最大流作为咽喉最大通过能力；刘庆伟等[2]提出了按股道别汇总并分析数据到发线能力的计算方法，为工业站到发线通过能力计算提供了一条可行途径.在技术站系统能力的既有研究中：李海鹰等[3]根据编组站到解系统列流到达特征，通过仿真模拟给出了货物列车等待列检、解体及空费系数等的计算公式.在既有研究中，大都采用确定型模型，考虑多种因素的不确定测度模型较少，而且能力在测定时往往还存在一定波动性.

在技术站能力的非定值表示研究方面：杨运贵[4]在分析车站作业不确定性的基础上根据贝叶斯区间估计原理，给出了车站能力的区间表示方法；方惠等[5]运用灰色系统理论，给出了咽喉道岔组通过能力的表示方法；李东[6]采用Bootstrap 估计法，给出了到发线通过能力的表示方法；谢迎春等[7]通过概率密度置信区间将不确定因素准确地反映到改编能力的计算过程中；王月[8]采用传统的区间估计对到发线通过能力的区间表示方法进行过相关研究；Zhao等[9]通过建立路径选择优化模型和设计相应的算法，提出了一种计算高速铁路车站通过能力的方法；Armstrong 等[10]对英国的铁路车站能力利用率与生产效率的关系进行了分析；Branishtov 等[11]提出了一种使用图表计算铁路通过能力的新方法.

对于区间不确定性的描述有很多方法，在诸多领域也有广泛应用.区间数具有上限和下限，并具有完全辨识不确定性信息的集合特征，相关学者对此进行了详细的研究：陈科宇[12]针对公交到站时间区间进行了预测，分析了重抽样、贝叶斯、Delta 分析、区间上下界估计等方法；陈小月[13]为了提高结构可靠性度量的准确性，提出在区间不确定性度量中引入泛灰数；丁先文等[14]将Bootstrap 方法与经典方法进行了比较.

从以上分析可知，在技术站能力表示及测定方面，既有文献大都利用确定性模型进行研究，难以体现能力的伸缩与动态性.本文利用三参数区间表征技术站能力，并界定松弛、平衡、收缩等能力概念.同时，引入泛灰数控制运算时引起的区间扩张，形成基于JAB（Jackknife-after-Bootstrap）区间估计的三参数区间泛灰数技术站能力表示与估计方法.

1 三参数区间泛灰数的描述

1.1 三参数区间

技术站能力在测定时存在有条件、有边界的波动范围，能力的上极限和下极限限定了其本身的范围，其数学表现形式为区间.其中，三参数区间是将取值可能性最大的中心点融入区间数，本文利用三参数区间的特性形成技术站能力的表示.三参数区间的中心点用区间的中值点表示，则三参数区间为

1.2 泛灰数

泛灰数作为灰数运算的补充，在灰色系统理论中起着重要作用.本文将泛灰数应用于三参数区间的表达，形成三参数区间泛灰数.根据技术站能力的研究对象，设论域为非负数，则三参数区间泛灰数为

式中：x为观测值；为x的灰信息部，表示对x的可信度范围，如泛灰数 (x,[0.4,1,1.6])表示x的可信值在0.4x到1.6x之间.

三参数区间泛灰数之间的运算准则为

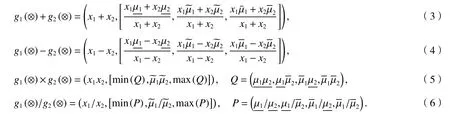
通过运算可以减少两个泛灰数的上下界运算关系，而且计算结果为函数区间的端点值.运算过程中区间上下界之间存在的相互作用会导致计算的值域范围扩大，形成区间扩张，而泛灰数可以避免这种情况.

2 基于三参数区间泛灰数的能力表示

泛灰数与区间数的表达式虽然不同，但可以互相转化.三参数区间可通过式（7）转化为泛灰数.

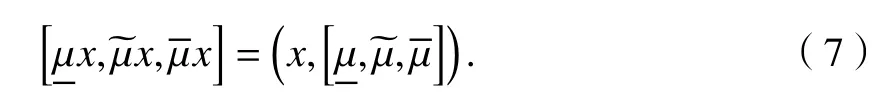
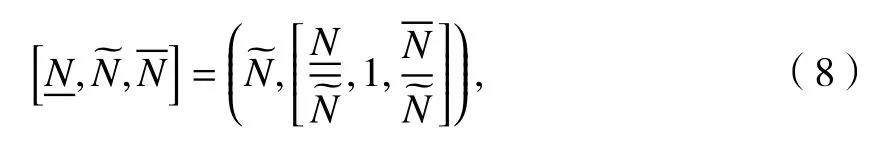
泛灰数能够有效解决由于表达式区间不同导致的区间扩张和分析结果差异问题.在进行技术站能力计算时，先将区间数转化为泛灰数，然后通过能力的计算步骤得到更为精确的计算结果.

3 技术站能力区间的估计方法

3.1 Jackknife 与Bootstrap 融合估计的基本方法与验证

Jackknife 和Bootstrap 两种方法在原理和计算方法上并不互相排斥，其本质都是对原始样本进行抽样重组和复制扩展.1992 年Efron 提出了将Jackknife与Bootstrap 估计融合的方法：先用Jackknife 法从样本中去除一个个体，再应用Bootstrap 方法估计样本统计量.通过文献[14-17]的算例进行模拟计算，对JAB 方法的有效性进行验证，计算结果见表1 和表2.

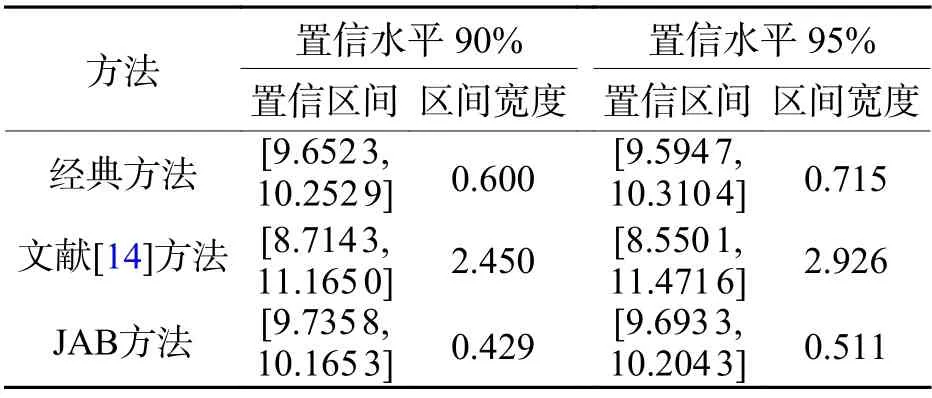
表1 文献[14]方法与JAB 方法的比较Tab.1 Comparison of the literature [14] method and the JAB method

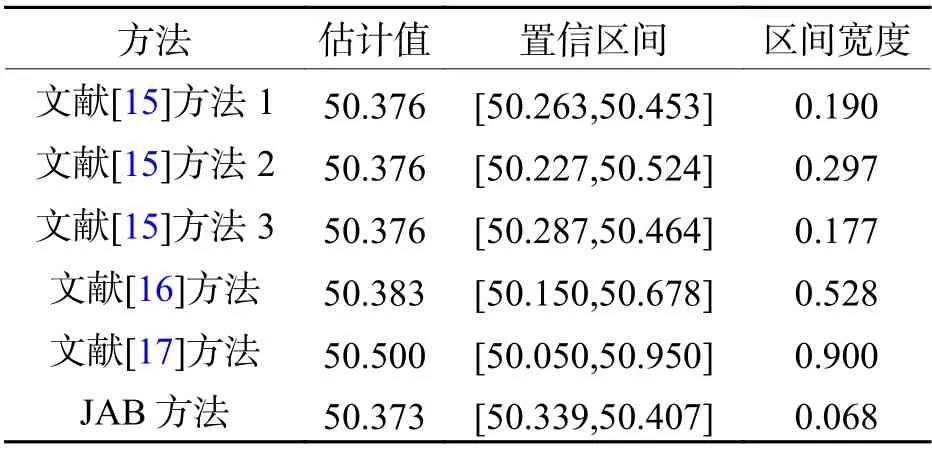
表2 文献[15-17]方法与JAB 方法的比较Tab.2 Comparison of the literature [15-17] method and the JAB method

通过对比可以看出，在区间宽度和区间位置上，JAB 方法比文献[14-17]所采用的方法更具优势，计算结果也更准确.

3.2 基于JAB 区间估计的能力计算步骤

以咽喉通过能力为例进行说明，具体步骤如下：

将基于JAB 区间估计得到的结果与文献[5,6,8]中方法进行对比，如表3.

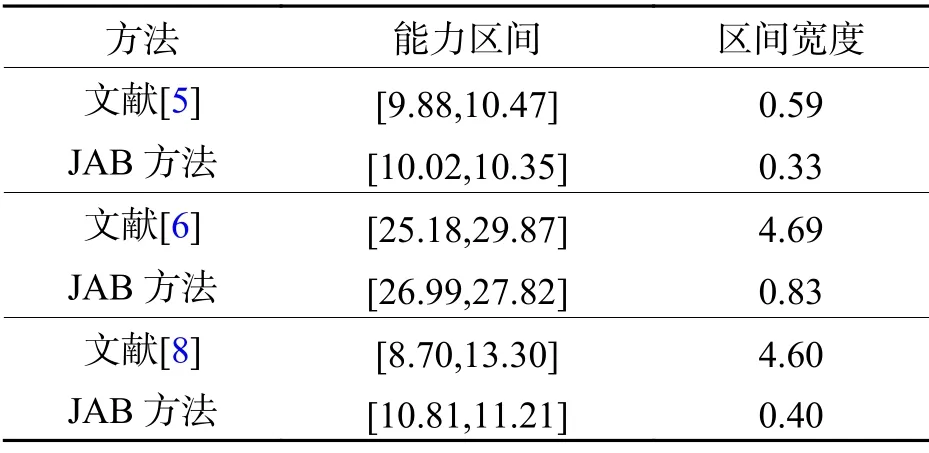
表3 能力不确定性描述方法的比较Tab.3 Comparison of methods for describing uncertainty of capacity

相比之下，杨运贵[4]所采用的贝叶斯区间估计法对累计总体信息、先验信息、样本信息等有严格的要求，这种方法不太容易操作，而谢迎春等[7]采用的概率密度法本质上还是将能力转化为定值.在区间位置和区间宽度上，本文提出的JAB 区间估计方法要优于方惠等[5]、李东[6]、王月[8]所采用方法计算出的“区间”能力，这说明基于JAB 区间估计方法具有良好的适用性.

4 实例分析

4.1 郑州北站上行系统通过能力估计

取郑州北站上行系统连续3 个昼夜的过程数据，以此为例基于三参数区间泛灰数对技术站能力进行表示与估计如表4.

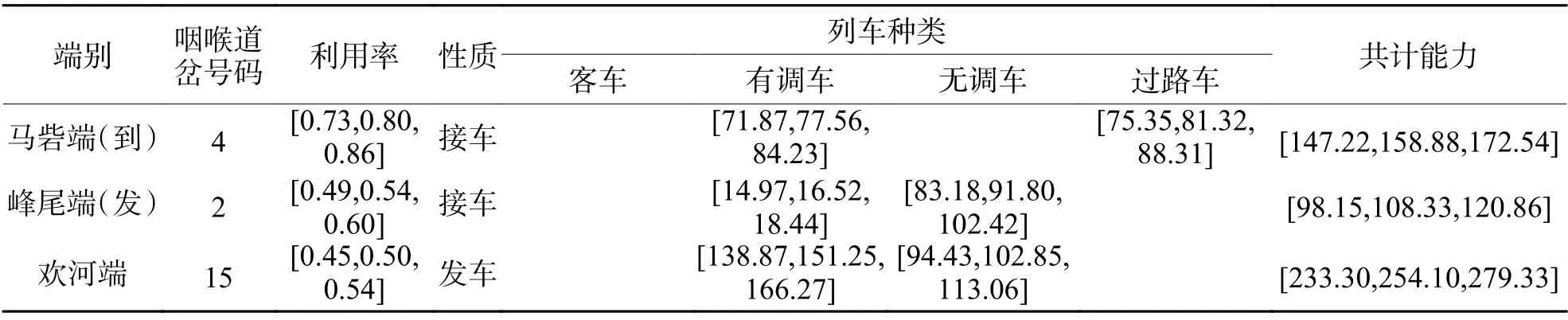
表4 上行系统咽喉接、发车能力Tab.4 Throat receiving-departure capacity of up system

对整个上行系统来说，到达场的过路车最终成为出发场的接入列车，因此不必计算过路车的能力，于是咽喉的接车能力为到达场和出发场接车能力之和（过路车除外）.过路车是指不在到达场停留，从到达场咽喉区直接运行至出发场的列车.

根据办理作业的列车数量可求得发线的通过能力，如表5 所示.

表5 上行系统到发线通过能力汇总Tab.5 Carrying capacity summary on arrival and departure track of up system

对比郑州北站上行系统咽喉接发车能力及到发线接车能力可知：到发线的能力为限制能力，且到发线对于通过能力的限制相对于咽喉来说更大.郑州北站上行系统最终通过能力为 239.43[0.99,1,1.01]列，平衡能力为239.43 列，收缩度为0.99，松弛度为1.01.郑州北站上行系统通过能力的总体情况如图1所示.

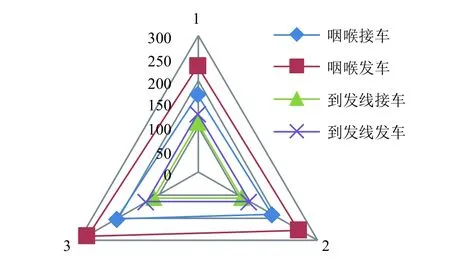
图1 郑州北站上行系统通过能力雷达图Fig.1 Radar figure for carrying capacity of up system in Zhengzhoubei station

4.2 郑州北站上行系统改编能力估计

由于技术站不同种类列车的作业方式存在差异，需要分别计算驼峰解体时单项作业的占用时间.利用“大型编组站能力数据获取与计算系统”进行汇总[19]，并根据汇总数据可计算得出解体一列车平均占用驼峰的时间tt为16.54[0.93,1,1.07] min.郑州北站上行系统驼峰的解体能力为

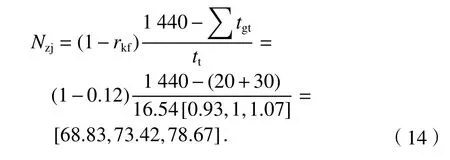
式中：rkf为郑州北站上行系统驼峰空费系数；tgt为驼峰固定作业时间.

相应地，郑州北站上行系统峰尾编组作业占用时间汇总如表6 所示.

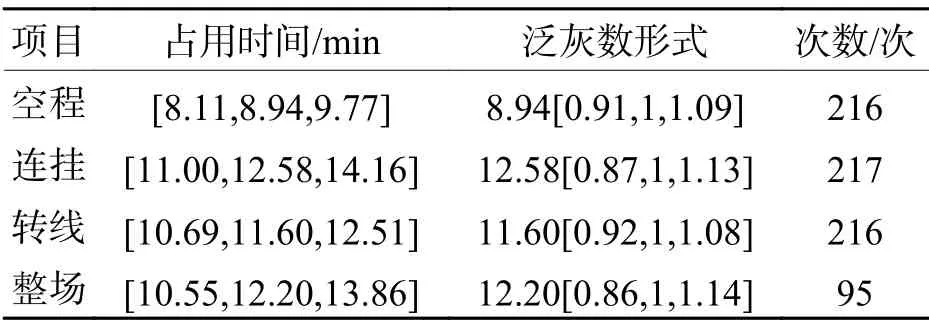
表6 峰尾编组作业占用时间Tab.6 Make-up occupation time on lead track

郑州北站峰尾牵出线能力利用率和峰尾编组能力分别为

式中：Tzq为郑州北站上行系统一昼夜全部作业占用牵出线设备的总时间；tgq为牵出线固定作业时间；Mqd为牵出线配备的编组调机台数；rq为郑州北站上行系统牵出线空费系数；nzb为郑州北站上行系统平均每昼夜编组的列车数.

综上，郑州北站上行系统驼峰解体能力为 [68.83,73.42,78.67] 列，峰尾编组能力为 [81.78,90.71,101.82]列，驼峰为能力的限制因素，不过二者基本平衡，差距不大.按照“纵列式编组站驼峰和峰尾分别当担解体和编组作业时，平衡二者作业负担后，以二者能力中较小者的两倍计算”的相关规定，郑州北站上行系统的最终改编能力Nzg为146.84[0.94,1,1.07]列，平衡能力为146.84 列，收缩度为0.94，松弛度为1.07.

汇总可得，郑州北站上行系统通过能力收缩-松弛度稳定在0.99～1.01 之间，系统的灵活性较小；改编能力收缩-松弛度在0.94～1.07 之间，略大于通过能力，不过同样在较紧张的范围内.郑州北站上行系统能力估计情况如表7 所示.

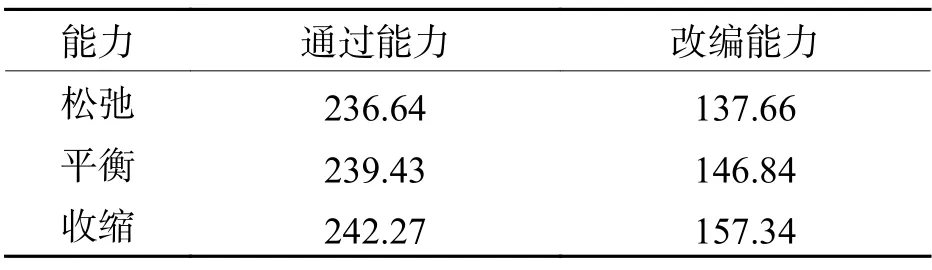
表7 郑州北站上行系统能力估计Tab.7 Capacity estimation of up system in Zhengzhoubei station

5 结 论

1）三参数区间数具有集合的作用，能够对能力的动态适应性进行测度，同时采用泛灰数可以削弱区间数运算过程中所产生的区间扩张问题；

2）将Jackknife 与Bootstrap 区间估计方法进行融合，通过比较可知JAB 区间估计法所计算出的技术站能力无论在区间位置还是区间宽度上均优于其它方法；

3）以郑州北站上行系统为例进行计算，得出其平衡通过能力为239.43 列，收缩度为0.99，松弛度为1.01；平衡改编能力为146.84 列，收缩度为0.94，松弛度为1.07.相较于原有的定值表示方法，更好地体现了能力的动态性和有界波动性.

致谢：综合交通大数据应用技术国家工程实验室开放基金项目（CTBDAT201902）.