高速列车的自适应容错跟踪控制
徐传芳
(大连交通大学 自动化与电气工程学院,辽宁 大连 116028)*
列车自动驾驶是未来高速铁路列车运行的发展趋势,是轨道交通领域的研究热点之一.对于高速列车自动驾驶技术的研究主要集中在两个方面:目标速度和位移曲线的优化以及对目标速度和位移优化曲线的跟踪控制[1-2].目前,在综合考虑安全性、准时性、节能以及乘坐舒适性等性能指标,计算目标速度和位移优化曲线方面已经取得了丰硕的研究成果[3-7].在得到速度和位移优化曲线后,如何通过设计高性能的列车跟踪控制算法,实现列车对优化速度和位移曲线的精确跟踪,就成为达到列车运行控制各项性能指标要求的关键,否则目标速度和位移曲线的优化也就失去了意义.
为此,很多学者对列车的速度与位移跟踪控制进行了研究[8-12].然而,文献[8-9]所提出的列车控制器依赖于部分列车模型参数.而实际上,列车模型参数难以精确获知,比如,列车质量会受到上下车旅客及其所携带行李的影响;基本阻力系数虽然可以通过风洞实验和实际运营所积累的数据获知,但在列车实际运行中,它们会随着线路状况、天气、列车质量等变化.为了应对列车模型参数不确定性的影响,文献[10-12]通过引入自适应控制技术,实现了不依赖于列车模型参数的精确速度和位移跟踪控制.然而,文献[10-12]并没有考虑执行器故障问题.列车在长时间、大距离、高速度运行中,执行机构不可避免地会发生电气故障或机械故障,出现部分失效甚至完全失效,这就需要系统具有自动应对此类故障的能力.被动容错控制不需要故障检测与诊断设备,不需要重组控制器[13-14],易于实现.然而,目前关于执行器故障下列车被动容错跟踪控制的研究成果还不够丰富.
本文考虑列车模型参数的不确定性和执行器效率部分损失故障,设计了列车的自适应容错跟踪控制器,并基于Lyapunov稳定性理论和仿真实验证明和验证了所提出控制器的有效性.
1 高速列车动力学模型
列车单质点模型受力分析简单,在模拟列车的运行效果时,具有实时、准确、快速的优点,在计算效率和精度方面具有较高的水平[15], 适合应用于要求快速、实时的场合,是列车运行控制中最常用的模型[16].其受力分析如图1所示.
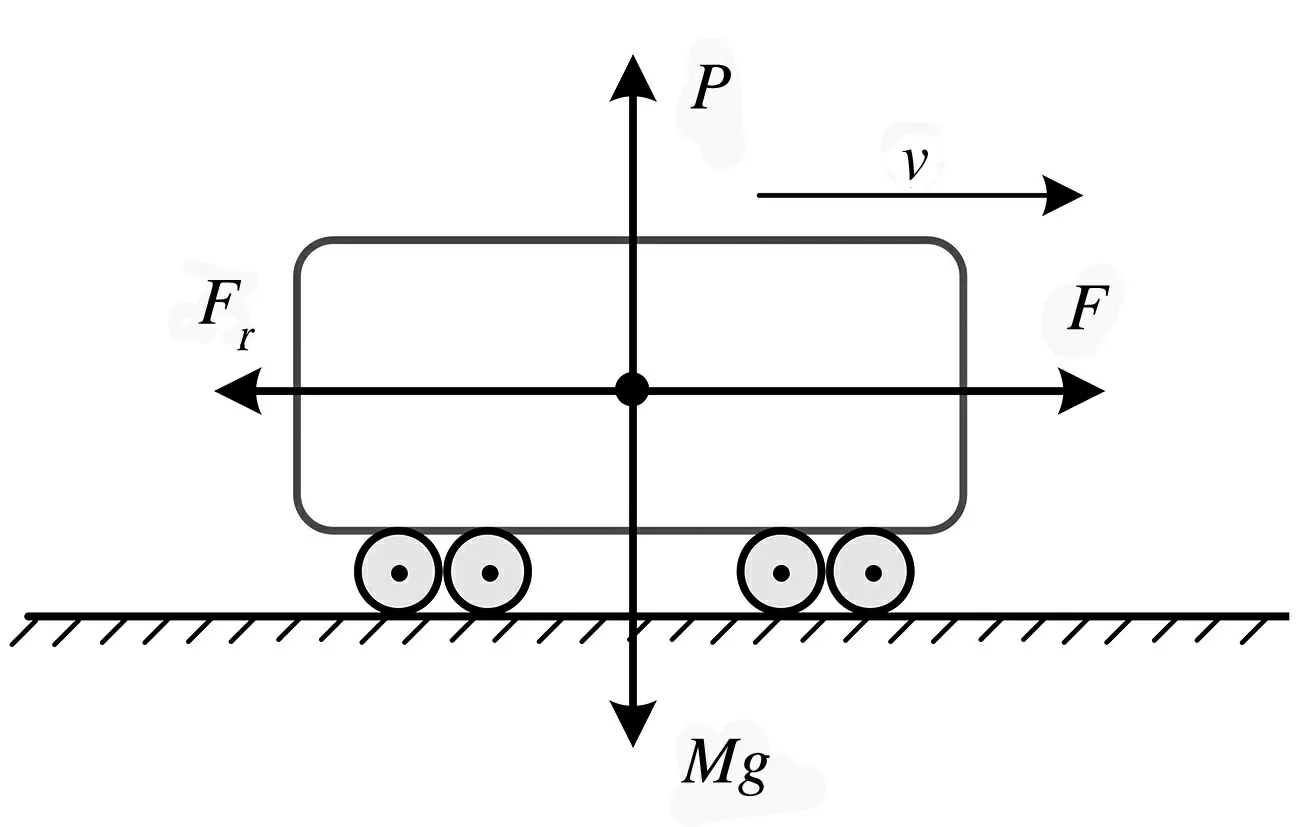
图1 列车单质点模型
图中,M为列车的总重量;g为重力加速度;v为列车的速度;F为列车牵引力或列车制动力,其中,在列车牵引阶段,F为列车牵引力,其方向与列车运行方向相同,在列车制动阶段,F为列车制动力,其方向与列车运行方向相反;Fr为作用在列车上的总运行阻力.
根据牛顿第二定律,列车单质点动态特性可以描述为
(1)
本文只考虑列车受到基本阻力情况.列车基本阻力主要由车辆部件和车辆表面与空气之间的摩擦,以及车轮与钢轨间的摩擦与冲击等产生,目前常采用经典的Davis方程来描述,即
Fr=a0+a1v+a2v2
(2)
式中,a0、a1、a2为正实数,一般可以从风洞试验和实际运营所积累的数据中获知,但实际运行中难以精确获知.
列车在线路上运行时,由于频繁的执行控制任务,执行机构不可避免地会出现故障,如电机过热或匝间短路故障、牵引变流器过电流故障、机械驱动器磨损故障等.这些故障可被分为卡死故障、失控故障、浮式故障和执行器效率损失故障等[17].其中,执行器故障比其他部件故障发生概率更高[18].本文针对执行器效率部分损失故障展开讨论.
执行器效率部分损失故障意味着执行器效率的部分损失,对于单质点列车动力学模型,可将此类故障看作一个整体[19].因此,发生执行器效率损失故障的执行器实际输出可描述为:
F′=kcF
(3)
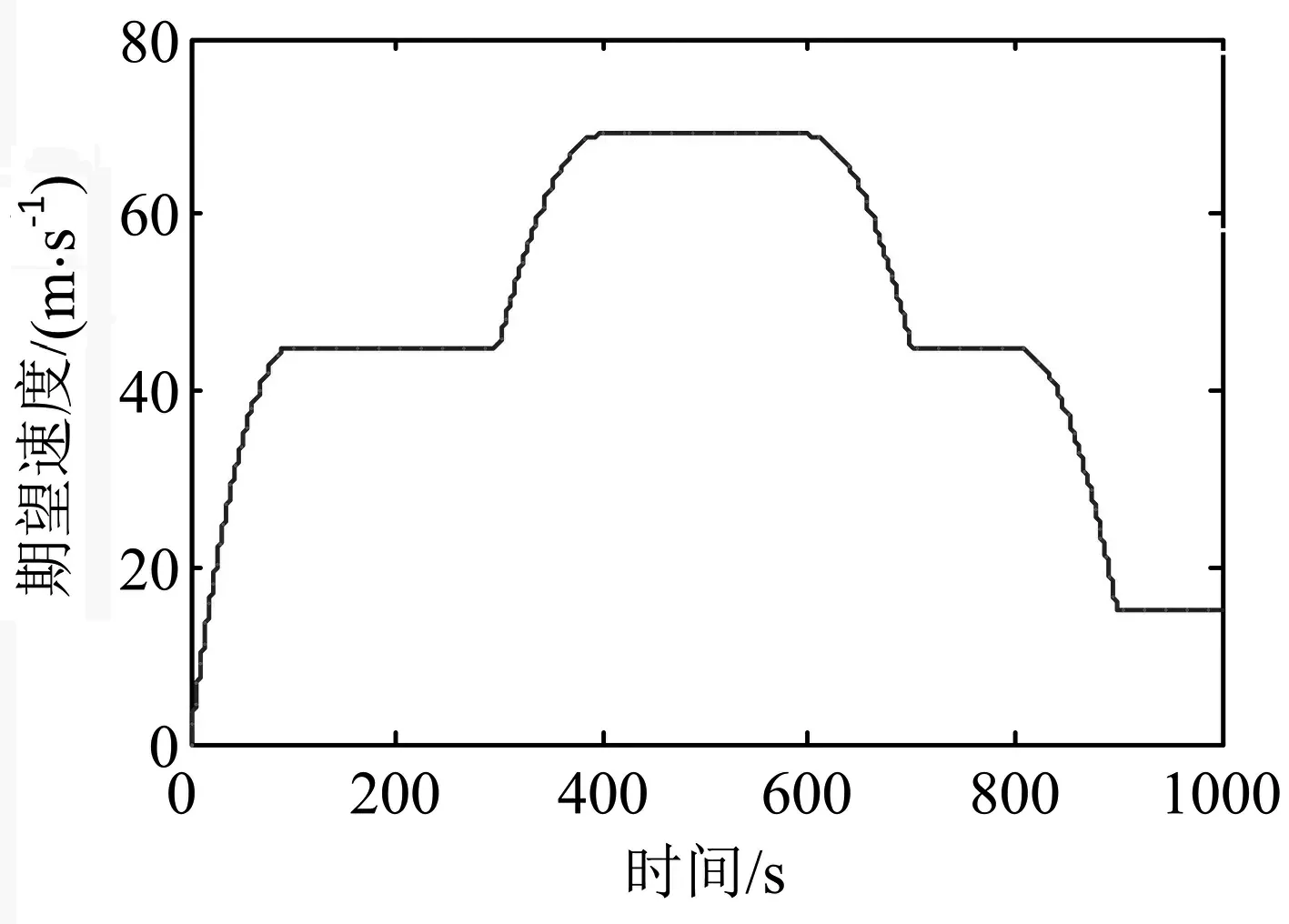
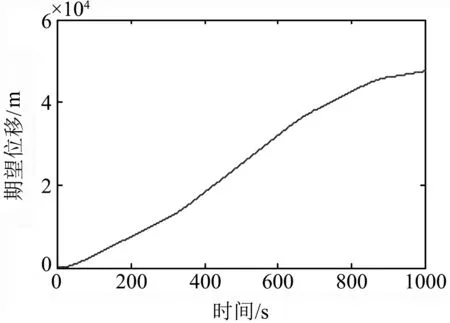
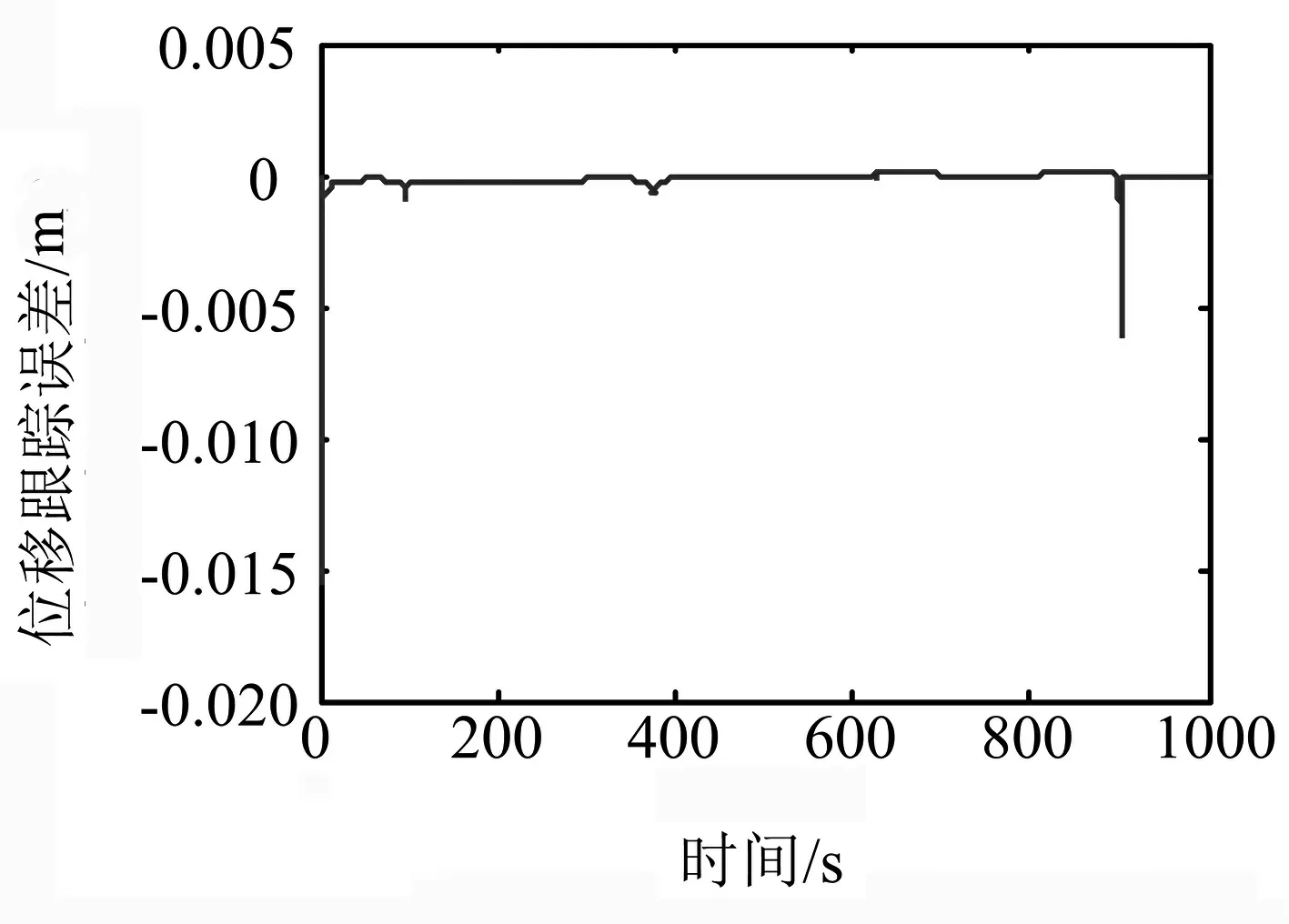
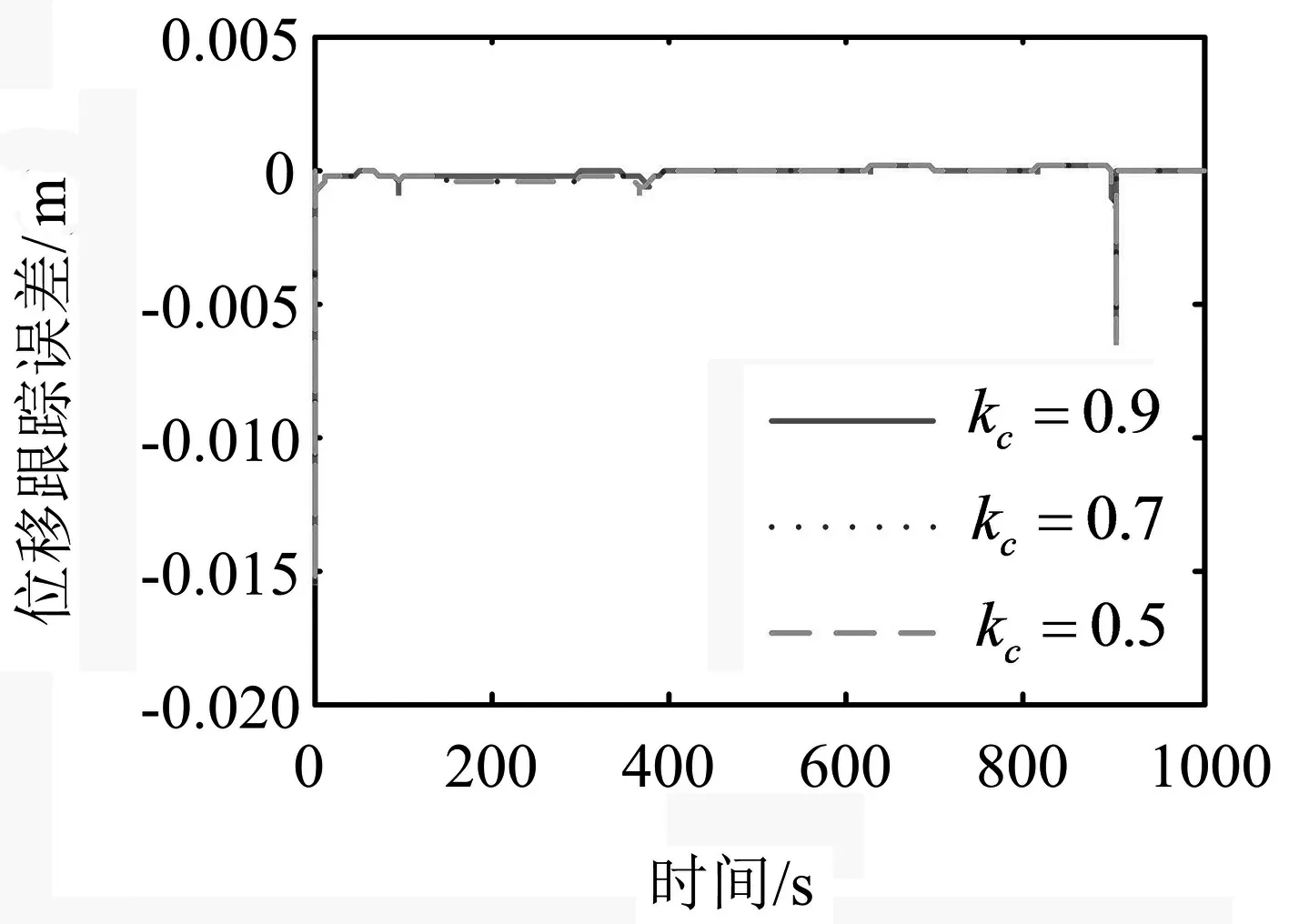
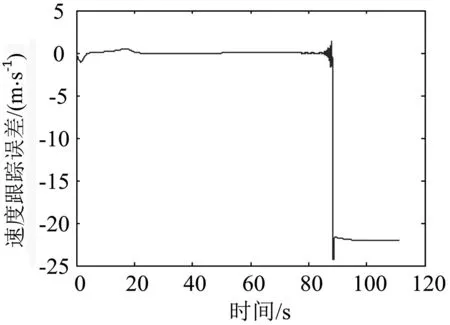
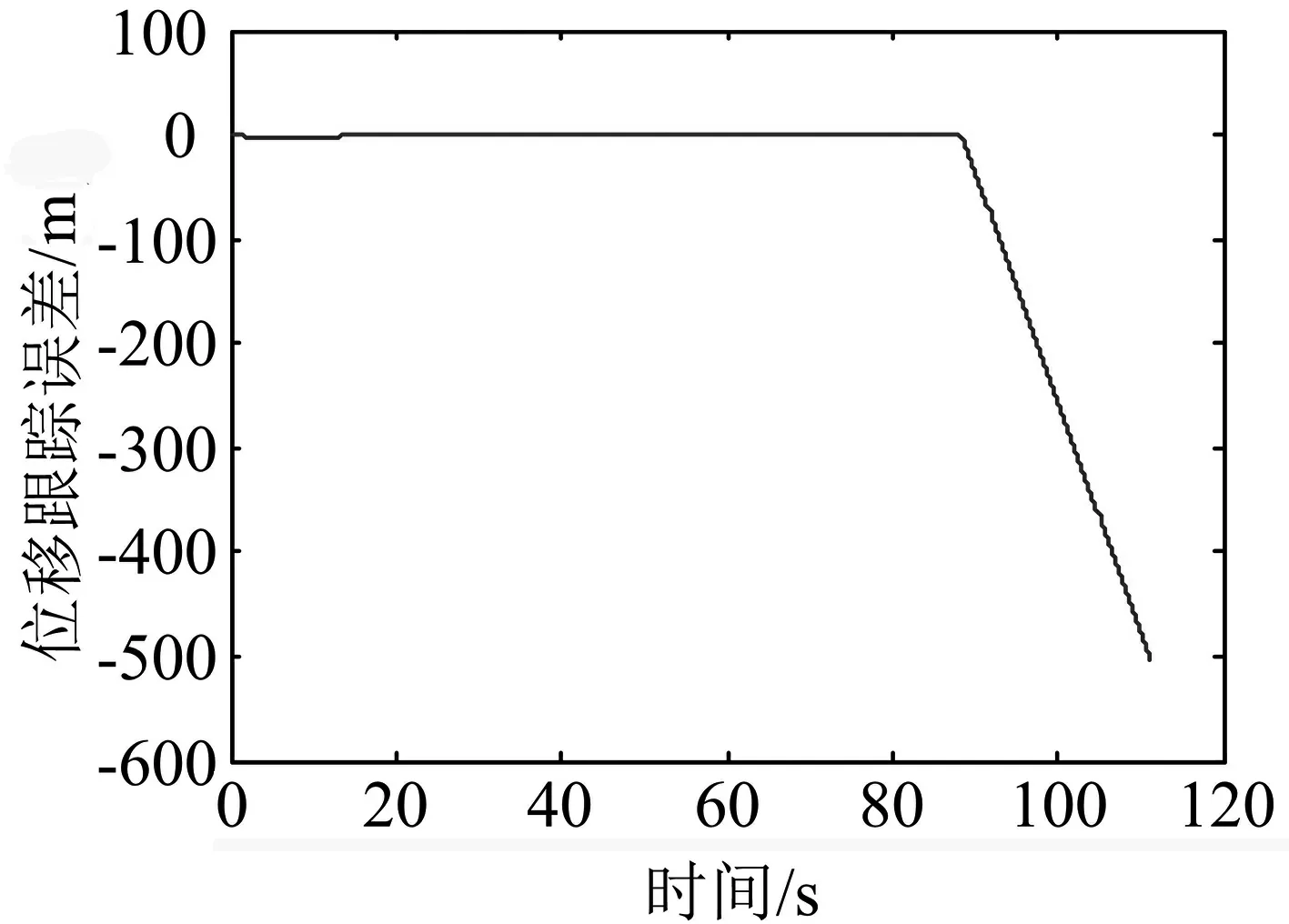
式中:F′为执行器的实际输出;F为不考虑执行器故障时的控制器输出;0≤kc≤1表示执行器效率,其中,kc=0表示执行器完全失效;kc=1表示执行器完全健康;0 考虑执行器效率部分损失故障,式(1)可写为 (4) 为了方便分析以及后文容错跟踪控制器的设计,定义kc=1-τc,则式(4)进一步变为 (5) 假设1假设0≤τc<δ<1,其中δ未知. 备注1:假设1表示即使执行器发生故障,它仍然有能力提供必要的驱动列车跟踪目标优化曲线的牵引力/制动力.当执行机构故障变得很严重,其所产生的最大牵引力/制动力不足以完成列车跟踪任务时,必须采取比如修正目标曲线等其他措施. 控制器的控制目标是:针对式(5)构成的系统,考虑列车模型参数不确定性和执行器效率部分损失故障,设计列车容错跟踪控制器,使得闭环系统稳定,列车能够精确跟踪目标速度和位移曲线. (6) 其中,β为任意选择的正实数.求s对时间的一阶导数,可得 (7) 结合式(5),可得到 (8) 基于自适应控制技术,本文设计的高速列车容错跟踪控制器形式如下: F=F0+F1+F2 (9) (10) (11) F2=-ks (12) 其中,k>0为控制器参数;sign(s)为符号函数. 设计未参数的自适应更新律分别为 (13) (14) (15) (16) (17) 对于本文设计的高速列车容错跟踪控制器,其主要结果总结为定理1. 定理1对于式(5)所描述的模型参数不确定且存在执行器效率部分损失故障的高速列车动力学模型,设计式(9)~(12)所示的容错跟踪控制器及式(13)~(17)所示的参数自适应更新律,则高速列车的速度跟踪误差和位移跟踪误差将渐进收敛到零. 证明:定义估计误差: (18) 选择Lyapunov函数 (19) 求V对时间的一阶导数 (20) 将式(8)和(9)代入式(20),可得 (21) 为了方便证明,将式(21)写为 (22) 其中,Φ1、Φ2和Φ3的表达式分别为 (23) (24) Φ3=s(1-τc)F2 (25) 将式(10)、(13)~(16)代入式(23),可以得到 (26) 结合式(11)、(17)及式(24),可得到Φ2满足如下关系 (27) 将式(12)代入式(25),可知 Φ3=-k(1-τc)s2≤-k(1-δ)s2 (28) 由式(26)~(28),式(22)变为 (29) 成立.此外,很明显闭环列车跟踪控制系统可以保证渐进稳定性,从而控制目标实现.证明完毕. 不考虑执行器故障时的高速列车自适应跟踪控制器由式(9)、(10)和(12)构成,未知参数自适应更新律见式(13)~(16).证明过程参照上文可以很容易得到,本文省略. 备注2:本文所提出的控制算法不依赖于模型参数的先验知识,不需要执行器故障信息,不需要故障检测和诊断设备.尽管引入了参数δ,但是它仅出现在证明过程,控制律和自适应更新律中均不需要δ. 为了验证本文所提出容错跟踪控制器的有效性,基于MATLAB软件进行了仿真验证.仿真所用列车参数为[21]:M=500 ton,g=9.8 N/kg,a0=5 880 N,a1=388 N·s·m-1,a2=8 N·s2·m-2. 控制器以及自适应更新律参数取值为:k=100,l0=10,l1=10,l2=10,lm=20 000,b=1000,仿真中涉及的参数初始值分别为: 为了减小抖振,使控制力平滑,本文采用边界层方法,当|s|≤ε,用s/ε代替sign(s),其中ε为一个很小的正常数. 为了验证所设计容错跟踪控制器的跟踪性能,仿真模拟了列车在1 000 s内的运行过程.整个过程运行距离为47.5 km,最高运行时速为69.5 m/s(约250 km/h),包含两个加速阶段,四个巡航阶段,两个减速阶段,所对应的目标速度和位移曲线如图2所示. (a) 目标速度曲线 (b) 目标位移曲线图2 目标速度和位移曲线 为了验证所提出控制器的可行性,首先对执行器未发生故障情况进行了仿真,列车的速度跟踪误差和位移跟踪误差如图3所示.可以看出,所提出的控制器实现了对目标速度和位移轨迹的精确跟踪.图3说明本文所提出的高速列车跟踪控制器是可行有效的. (a) 速度跟踪误差 (b) 位移跟踪误差图3 执行器未发生故障时的跟踪误差 为了验证所提出控制器的容错跟踪能力,对执行器不同程度效率损失故障下的列车跟踪控制系统进行了仿真.通过改变执行器有效系数kc的数值,来模拟不同程度的执行器故障.假设执行器故障发生在150 s,并持续到仿真结束.仿真中考虑了执行器效率损失分别为10%、30%和50%(分别对应kc=0.9、kc=0.7和kc=0.5)三种情况.列车的速度跟踪误差和位移跟踪误差如图4所示. kc减小,意味着执行器效率降低,执行器故障程度越来越严重,故障对列车跟踪运行的影响也越来越大.但是,从图4可以看出,速度跟踪误差和位移跟踪误差并没有随着执行器故障程度的严重显著增加,而是始终保持较小数值.图4表明, 所提出的控制器能够补偿执行器效率损失故障,具有良好的容错跟踪能力. (a) 速度跟踪误差 (b) 位移跟踪误差图4 执行器不同程度故障下的跟踪误差 为了说明考虑执行器故障设计跟踪控制器的必要性和有效性,对实际执行器存在故障,但跟踪控制器设计过程并未考虑执行器故障的情况进行了仿真.当执行器效率损失为30%(即kc=0.7)时,高速列车的速度跟踪误差和位移跟踪误差如图5所示. (a) 速度跟踪误差 (b) 位移跟踪误差图5 不考虑执行器故障设计跟踪控制器的跟踪误差 可以看出,未考虑执行器故障设计的跟踪控制器,在存在执行器故障时,系统的速度跟踪误差和位移跟踪误差大幅增加,系统跟踪效果变得很差.对比图5和图4中kc=0.7时的仿真结果可以看出,考虑执行器故障设计跟踪控制器是必要的,本文所设计的容错跟踪控制策略是有效的. 本文针对高速列车自动驾驶中的速度和位移跟踪控制问题,建立了存在模型参数不确定性和执行器效率部分损失故障的列车动力学模型,设计了列车的自适应被动容错跟踪控制器,并进行了严格的理论证明和仿真验证.所设计的容错跟踪控制器不仅实现了列车执行器故障下的精确跟踪控制,而且不需要模型参数的先验知识,不需要故障检测与诊断模块,使得列车在运行中,在模型参数不断变化以及发生执行器效率损失故障的情况下,不必重新设计列车跟踪控制器.基于Lyapunov稳定性理论证明了列车的速度跟踪误差和位移跟踪误差可以收敛到零.仿真结果显示了该控制器的可行性、应对执行器效率部分损失故障的有效性,以及良好的容错跟踪能力.本文以单质点列车动力学模型为研究对象,对执行器故障的设定较为简单.针对多质点列车动力学模型,更加合理地对执行器故障进行描述和设定,设计高速列车的容错跟踪控制器是接下来的研究方向.2 控制器设计及稳定性分析
2.1 控制器设计
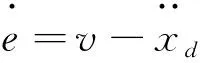
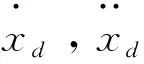
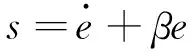
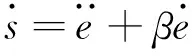

2.2 稳定性分析
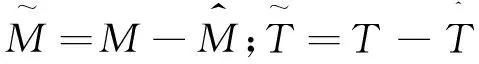

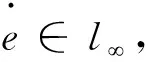
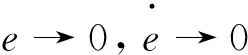
3 仿真验证及分析


4 结论

