关于等差数列在三素数中的分布
储玉结
(合肥工业大学 数学学院,合肥230601)
1 引 言
记x为充分大的实数,整数k≥2.集合Dk={d1,…,dk},其中d1 其中p遍历全体素数,vDk表示集合Dk的元素模p后的剩余类个数.使得S(Dk)≠0的集合Dk被称为容许集.π(x,Dk)表示使得n+d1,…,n+dk都是素数的正整数n≤x的个数.当Dk不是容许集的时候,π(x,Dk)是不超过k的有界值,因此只关心容许集的情形.1923年Hardy和Little wood[1]根据圆法猜测出了π(x,Dk)的主项,并提出了著名的Hardy-Littlewood猜想.后来带余项的一致性渐进公式也同样被称为Hardy-Littlewood猜想,参见[2].1974年Halberstam和Richert[3]给出了π(x,Dk)的一个上界,即 (1) 其中ε表示给定的任意小的正数.本文关心三素数的分布情况,即k=3的情形,为了表达方便,下文简记D3为D,具体来说,将考虑 与D的关系,这里D={0,d1,d2}.显然有G3(x,D)=π(x-d2,D),因此将用到k=3时的Hardy-Littlewood猜想,具体如下: 猜想1若S(D)≠0,则对∀ε>0,在2≤d2≤(1-ε)x上一致有 等差数列是重要的数学对象,关于它有很多有意思的研究,如最近的工作[4-5].当等差数列的各项都是素数时称为素数等差数列.素数等差数列是数论界非常关心的问题,数学界著名的Green和Tao证明了素数中存在任意长的等差数列,但是目前仍然无法得到很多关于公差的信息.本文将在著名的Hardy-Littlewood猜想下,一方面试图去进一步认识长为3的素数等差数列的公差分布信息,另一方面,鉴于素数最可能的差集最近被广泛研究如[6],因此在这里,自然考虑了出现频率最高的长为3的等差数列是否是三素数最可能的分布形式. 首先由猜想1导出G3(x,D)的渐进公式. 引理1假设猜想1成立,则在2≤d2≤(1-ε)x上一致有 (2) 其中 证对猜想1中的积分项三次分部积分得 在2≤d2≤(1-ε)x上有 所以 代入得引理1. (3) 由(3)式,不难看出,影响G3(x,D)值的因素主要来自三个方面,一方面是奇异级数S(D),另一方面是x-d2,最后一方面来自函数H(x,D).下面将给出关于这三方面的一些估计.用ω(d)来表示d互异的素因子个数,则由奇异级数的定义易知 (4) (5) (6) 本节将讨论长为3的素数等差数列出现频率最高的公差问题,具体结论如下: 定理1设δ是一个给定的小实数,基于猜想1: (7) 定理1的证明由以下两个引理构成. P#a=1-δ()xlogx#, 以及 将上面三式代入(3),整理得 P#b=1+δ()xlog2x#, 再由(3)得 将上面三式代入(3),整理得 其中 所以 综合以上五种情形,引理3得证. 本节通过构造一个具体的例子来说明,定理1中的素数等差数列并不一定是三素数最可能的分布形式. 又因为 所以,由上面三式及(2)得 本文研究了长为3的素数等差数列出现频率最高的公差问题.基于Hardy-Littlewood猜想,通过分类讨论,证明了长为3的素数等差数列频率最高的公差是素数连乘.通过构造一个反例,发现这个频率最高的素数等差数列并不一定是三素数出现次数最多的分布. 致谢作者非常感谢审稿专家对论文提出的宝贵建议.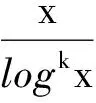
2 渐进公式
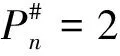

3 长为3的素数等差数列最可能的公差

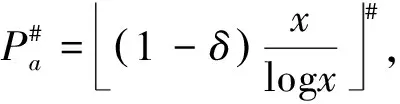
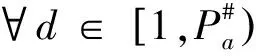
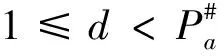
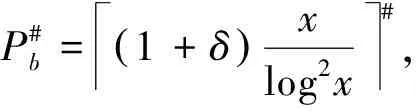
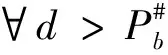
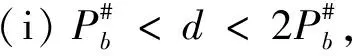

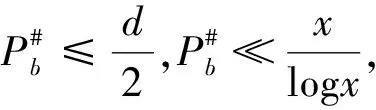
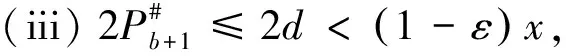
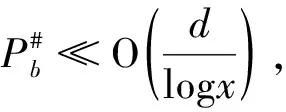
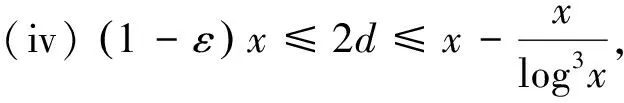
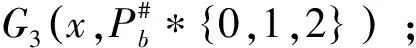

4 关于三素数最可能的分布
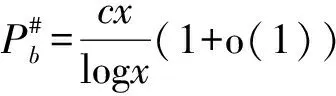

5 结 论

