适用于中压领域的V形钳位多电平变换器

原露恬 王琛琛 薛 尧 杨晓峰 郑琼林

适用于中压领域的V形钳位多电平变换器

原露恬 王琛琛 薛 尧 杨晓峰 郑琼林

（北京交通大学电气工程学院 北京 100044）

多电平变换器在中高压大功率电能变换领域已得到广泛的应用。该文针对中压电能变换领域，提出V形钳位多电平变换器（VMC）拓扑族。在现有IGBT电压等级的条件下，该拓扑族采用较少数量的器件就可以实现中压大功率电能变换，结构简单；同时该拓扑族无需飞跨电容，降低了系统控制复杂度。首先提出VMC拓扑族的构成，包括拓展方式、一般形式以及演化类型；在此基础上研究VMC工作原理及控制方法，分析直接钳位机制和阻断电压分配问题。考虑目前商业主流功率器件电压等级，针对拓扑结构特点，揭示适宜VMC的电压等级；最后通过仿真和实验结果验证了所提拓扑族及控制方法的可行性，也进一步证明了该文理论分析的正确性。

多电平变换器 电能变换 共直流侧电容 直接钳位 V形钳位

0 引言

由于开关器件具有电压应力低、输出波形谐波含量低、系统电磁干扰（Electromagnetic Interference, EMI）低等优势，因而多电平变换器自问世以来就受到了工业界和学术界的广泛关注，成为目前中高压大容量电能变换领域的研究热点之一[1-4]，在交流调速[5]、电能质量改善[6-7]以及可再生能源接入[8]等场合中都得到广泛的研究和应用。

文献[9]最先提出利用多个电压电平进行功率转换的思想，即在每级直流源两端引出可控通路以输出多电平。但是由于当时开关器件发展水平的限制，采用反并联的晶闸管来实现全控开关的功能，晶闸管关断不可控的缺点造成换流过程极其复杂，控制难度高，故该结构没有得到推广与应用[10]。同时，该方法会导致部分开关管承受整个直流母线电压[11]。

中点钳位（Neutral-Point-Clamped, NPC）型多电平变换器[12]是目前商业化应用最广泛的变换器类型。然而NPC也存在一些缺点，如随着输出电平等级的增加钳位二极管数量快速增加，内侧开关管的间接钳位等。在此基础上，文献[13]提出了一种具有冗余状态的飞跨电容（Flying-Capacitor, FC）型多电平变换器。但是随着电平数的增多，FC的数量急剧增多，并且在多相系统中，飞跨电容的平衡控制也更为复杂[14]。级联H桥（Cascaded H-Bridge, CHB）型多电平变换器由于其模块化结构，被广泛应用于高压电机驱动领域中[15]。但CHB需要昂贵且笨重的移相变压器来提供隔离的直流电源，这使得系统成本和体积大大增加[16]。

近些年又涌现出一些新型多电平变换器拓扑，如模块化多电平变换器（Modular Multilevel Converter, MMC）、层叠式多电平变换器（Stacked Multicell Converter, SMC）和有源中点钳位变换器（Active Neutral-Point-Clamped, ANPC）。MMC的优势在于它的模块化和扩展性，其被广泛应用于高压直流输电（High Voltage Direct Current Trans- mission, HVDC）系统[17]。然而MMC存在控制复杂的问题（如模块电容电压平衡控制和环流抑制控制），且不适合于低速高转矩的传动场合[18]。SMC和ANPC在保持FC优势的同时，大大减少了钳位器件的数量[19-20]。然而，多相系统仍然需要一定数量的飞跨电容，仍存在变换器成本和体积增大、控制复杂等问题[21]。值得注意的是，ANPC存在输出电压多电平跳变和串联开关管动态均压问题，引起较高的d/d，严重时可能会导致变换器和电机无法安全运行[22]。

本文首先提出适用于中压电能变换领域的V形钳位多电平变换器（V-clamp Multilevel Converter, VMC）[23-24]拓扑族。该拓扑族无需飞跨电容，且大大减少了钳位器件的数量，使得拓扑结构和控制都更为简单。其次，通过介绍该拓扑族的扩展方式、一般形式及演化类型，具体展示了VMC拓扑族的结构特点。然后，研究了拓扑族的工作原理和控制方法。接着，分析了直接钳位机制和阻断电压分配问题。最后，将VMC与其他典型多电平变换器进行详细对比，揭示VMC适宜电压等级。通过仿真和实验结果，验证了所提拓扑族及控制方法的可 行性。

1 VMC拓扑族

本节将介绍VMC拓扑由低电平向高电平的拓展方式、奇数电平和偶数电平的一般形式以及VMC拓扑的其他演化类型。VMC奇数电平拓展方式如图1所示。

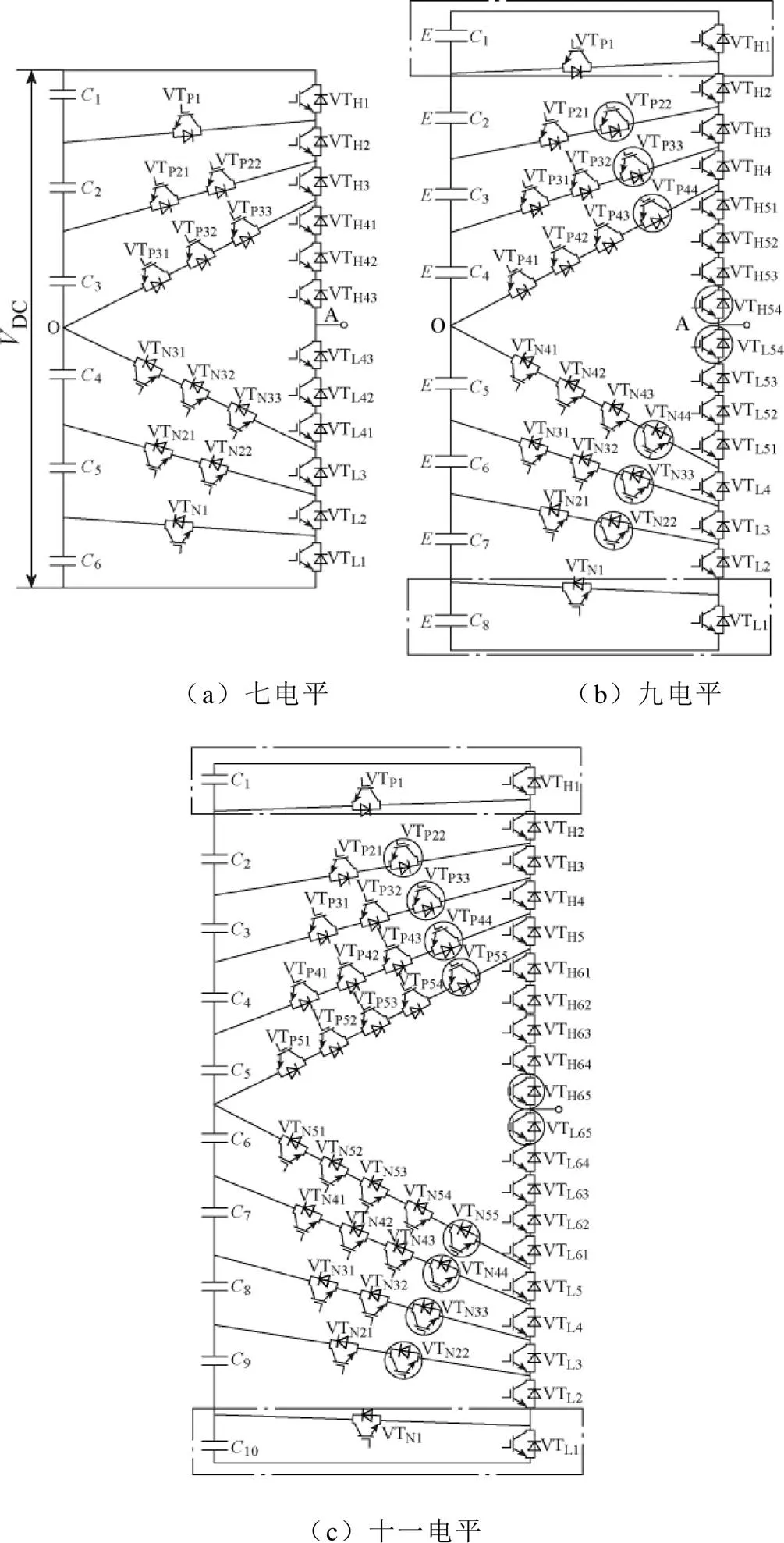
图1 VMC奇数电平拓展方式

1.1 VMC拓展方式

图1a为VMC七电平变换器，包含直流母线电容、输出功率桥臂以及6条钳位支路。每个直流母线电容的额定电压均为一个电平等级（=DC/6）。上半桥臂的钳位支路为正向，开关管中反并联二极管的电流从直流母线电容流向交流侧A点；下半桥臂的钳位支路为反向，开关管中反并联二极管的电流从交流侧A点流向直流母线电容。通过6条钳位支路将直流侧电容和输出功率桥臂的对应节点相连，即可实现七电平的输出。图1b为VMC九电平变换器，VMC七电平向九电平拓展的过程可以表示为：用点画线框中的半桥结构代替七电平变换器的正母线和负母线，则可以得到九电平变换器，添加圆圈标记的串联开关管以保证每个开关管的额定电压保持一个电平等级，该结论将在下文详细分析。按照同样的拓展方式可以得到如图1c所示的VMC十一电平变换器。

VMC偶数电平拓展方式如图2所示。图2a为VMC八电平变换器，只需在图1a所示的七电平VMC的直流侧中点添加一个电容，在输出功率桥臂添加两个开关管即可得到，如图2a所示圆圈标记的电容和开关管。同样地，十电平VMC也可以由同样的方法由图1b所示的九电平VMC得到，如图2b所示。

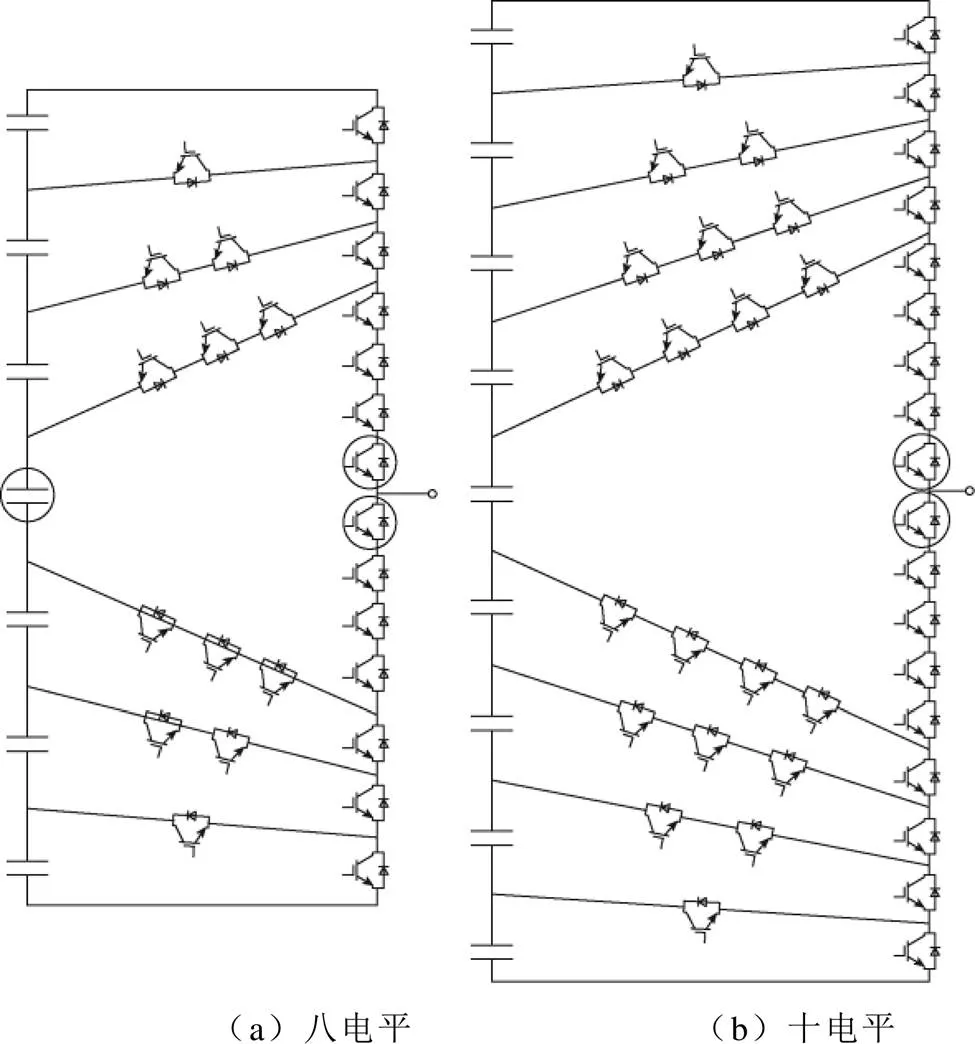
图2 VMC偶数电平拓展方式

由此可见，VMC拓展方式简单，如果不考虑实际因素限制，VMC可拓展至任意电平。同时，若将奇数电平VMC增加一个电平拓展至相邻的偶数电平，只需在直流侧电容上串联一个电容和在每相输出功率桥臂上串联两个开关管即可。

1.2 VMC一般形式

VMC一般形式如图3所示。图3a给出了2+1（为正整数）电平VMC的一般形式，其需要2个直流侧电容以及(+5)个开关管。2+1电平VMC包含条正向钳位支路和条反向钳位支路，2个串联的直流侧电容将直流母线电压分为2+1个电平。

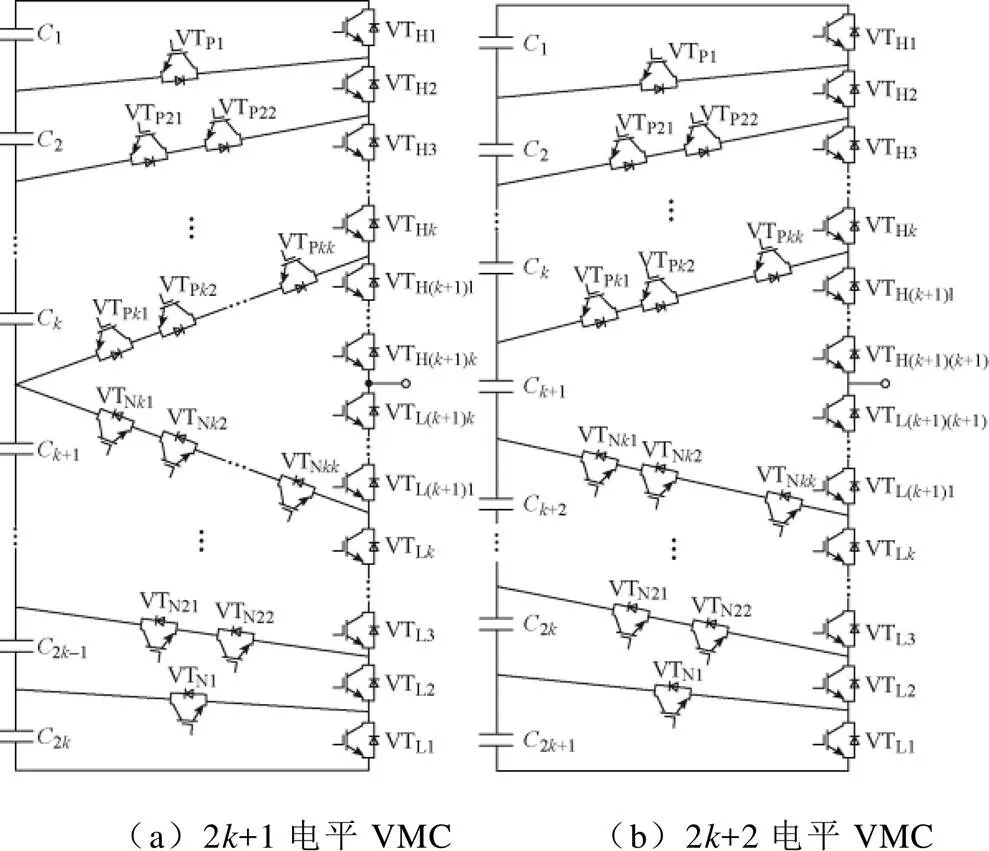
图3 VMC一般形式

图3b为输出2+2电平VMC的一般形式，其需要2+1个直流侧电容以及(+5)+2个开关管。同理，将VMC从2+1电平扩展到2+2电平，只需在直流侧电容上串联一个电容和在每相输出功率桥臂上串联两个开关管。在三相系统中，三相变换器共用直流侧电容，每相无需飞跨电容。VMC仅通过带反并联二极管的开关管即可实现功率的双向流动。

1.3 VMC其他演化类型

观察1.2节中提到的VMC拓扑一般形式，奇数电平VMC存在零电平冗余通路，将零电平通路变形可以得出VMC拓扑的其他拓扑演化类型。值得注意的是，这些演化类型只适用于奇数电平VMC。

以图1a为例，当输出零电平时，电流可经由最内侧的两条钳位支路开关（VTP31、VTP32、VTP33和VTN31、VTN32、VTN33）流向交流侧，这两条支路的电流分配率取决于支路导通特性。VMC拓扑演化类型如图4所示。将图1a最内侧钳位支路开关用其反并联二极管代替，则可得到VMC类型Ⅱ，如图4a所示。当输出零电平时，两条二极管钳位支路可以分别提供正向和反向的电流通路，进一步节省了器件成本。文献[24]即以该种类型为研究对象展开研究。

将VMC中最内侧的两条钳位支路开关保留任意一条，仍然可以实现多电平的输出，形成如图1b和图1c所示的非对称上侧开关管钳位型（类型Ⅲ）和非对称下侧开关管钳位型（类型Ⅳ）结构。类型Ⅲ和类型Ⅳ每相拓扑比VMC少用个开关管。

图4 VMC拓扑演化类型

将VMC中最内侧的两条钳位支路开关反向串联至直流母线电容中点O点和输出功率桥臂中点A点之间，可以得到VMC类型Ⅴ，如图4d所示。此时，中点钳位支路的开关管VTP31、VTP32、VTP33、VTN31、VTN32、VTN33导通构成零电平电流通路。VMC拓扑演化类型在工作原理相似的基础上又有各自的特点，需根据不同场合进行选择。

2 VMC工作原理及控制方法

针对第1节中提到的十一电平VMC，本节主要介绍该变换器拓扑的工作原理及调制方法。十一电平VMC拓扑如图5所示。

同向串联连接的开关管应同时动作，例如，输出功率桥臂中的串联开关管VTH61、VTH62、VTH63、VTH64、VTH65状态相同，用VTH6统一表示。同理，其他同向串联开关也应同时动作，他们的开关状态也分别统一表示，如图5括号中的字体标注（VTH6, VTL6, VTP2, VTP3, VTP4, VTP5, VTN2, VTN3, VTN4, VTN5）。为防止直流侧电容短路，开关管（VTH1, VTP1）、（VTH2, VTP2）、（VTH3, VTP3）（VTH4, VTP4）、（VTH5, VTP5）、（VTL5, VTN5）、（VTL4, VTN4）、（VTL3, VTN3）、（VTL2, VTN2）、（VTL1, VTN1）应分别互补动作。

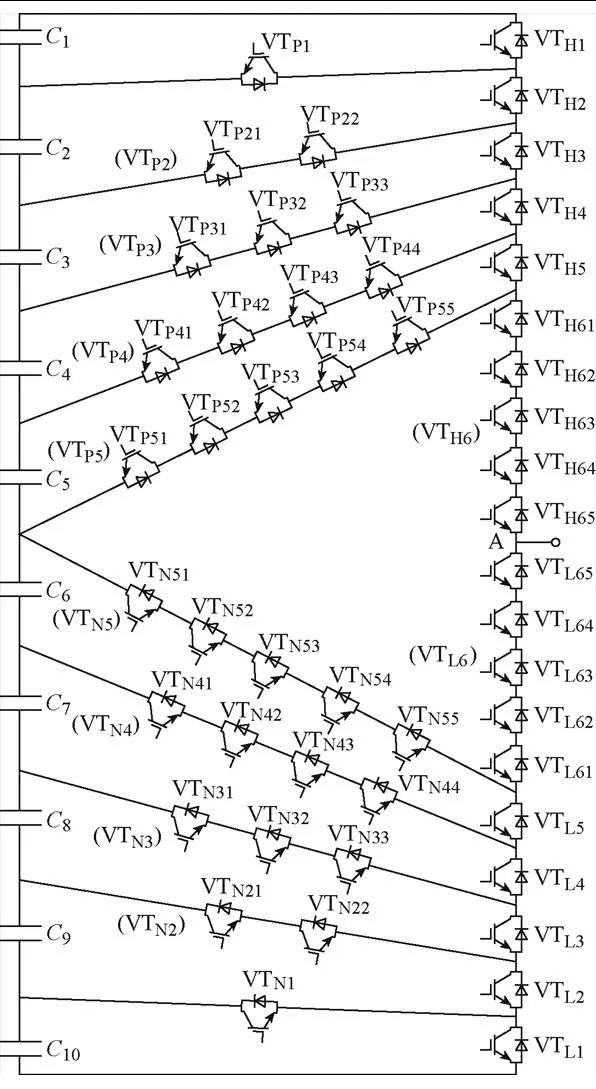
图5 十一电平VMC拓扑

十一电平VMC开关状态见表1，表中，o为输出电压，H1～H5、L5～L1为功率桥臂上各开关管的门极信号，VTH6和VTN5信号一致，VTL6和VTP5信号一致。以O点为参考点，通过控制开关管的通断，可在A点和O点之间得到+5、+4、+3、+2、+、0、-、-2、-3、-4、-5共十一种电平状态。

表1 十一电平VMC开关状态

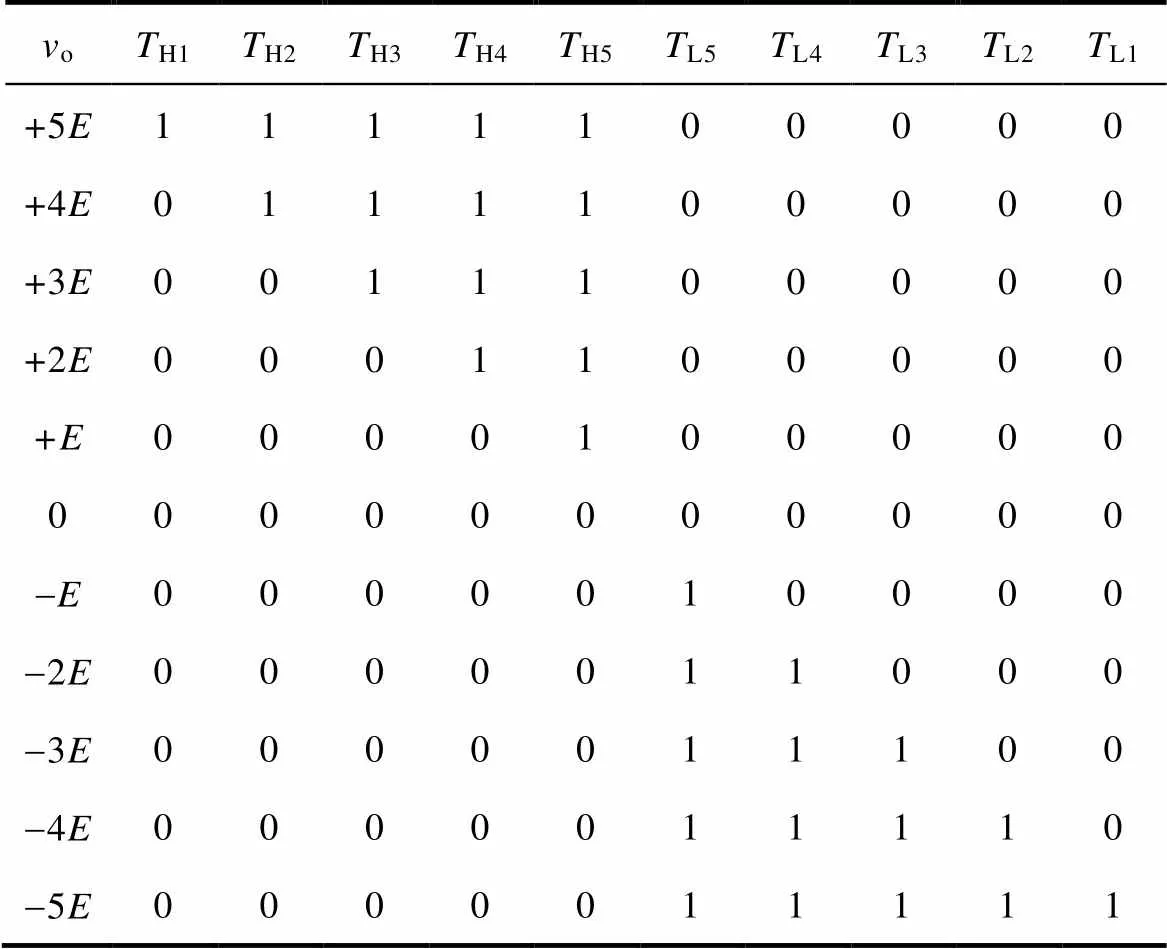
Tab.1 Switch states of eleven-level VMC

注：1表示导通；0表示关断。

交流侧产生的输出电压可用以下开关函数建模，即

拓展到一般形式的VMC拓扑，对于2+1奇数电平VMC，交流侧产生的输出电压表示为

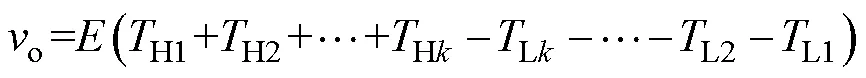
式中，以直流母线中点O为参考点，输出电压o的范围为-～+。

对于2+2偶数电平VMC，开关管VTH(k+1)和VTL(k+1)的状态互补，其他开关状态均与奇数电平相似。偶数电平没有直流母线中点，当以直流母线最低点为参考点时，输出电压o的范围为0～+(2+1)。2+2偶数电平VMC交流侧产生的输出电压为

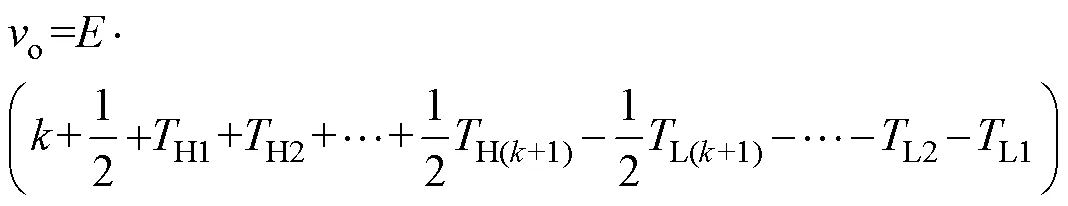
通过多载波层叠正弦脉宽调制（Sinusoidal Pulse Width Modulation, SPWM）技术可实现上述开关状态。将基频正弦调制波信号和同相层叠的同频率同幅值的10组载波信号相比较，得到相应开关管的驱动信号，从而控制开关管导通或关断以输出相应电平。值得注意的是，VMC拓扑结构中所用到的开关器件串联结构与传统意义上的开关器件串联工作机理不同。VMC变换器中的串联支路开通和关断前后，该工作支路两端所承受的电压只变化一个电压等级，即每个开关瞬态过程该串联开关的阻断电压最多为一个电平电压，避免了复杂的动态均压措施。

3 VMC直接钳位机制和阻断电压分配

间接钳位问题是二极管钳位型多电平变换器的主要缺点之一[25]，二极管钳位型多电平变换器中内部开关管实际上没有直接钳位到直流侧电容两端，由于系统杂散电感的存在，其会导致内部开关的静态过电压问题[26]。VMC在采用上述开关状态时，输出功率桥臂上的独立开关管被直接钳位到直流侧电容两端，有利于开关管之间的电压分配和可靠钳位。

VMC直接钳位机制如图6所示，以输出+5电平为例，展示VMC中开关管的钳位机制。其中，VTL1经回路11被10直接钳位，承受10两端的电压；VTL2经回路10被9直接钳位，承受9两端的电压；VTL3、VTL4、VTL5分别经回路9、8、7钳位到相应的直流侧电容两端，承受单个直流侧电容电压；VTL6经回路6被1～5直接钳位，承受1～5两端的电压。可以看出，下桥臂内部开关管和外侧开关管静态时承受的电压等级相同，都为一个直流侧电容电压。类似地，当输出-5电平时，上侧桥臂的开关管都直接钳位到直流侧电容两端，每个开关管的静态承压为一个直流侧电容电压。

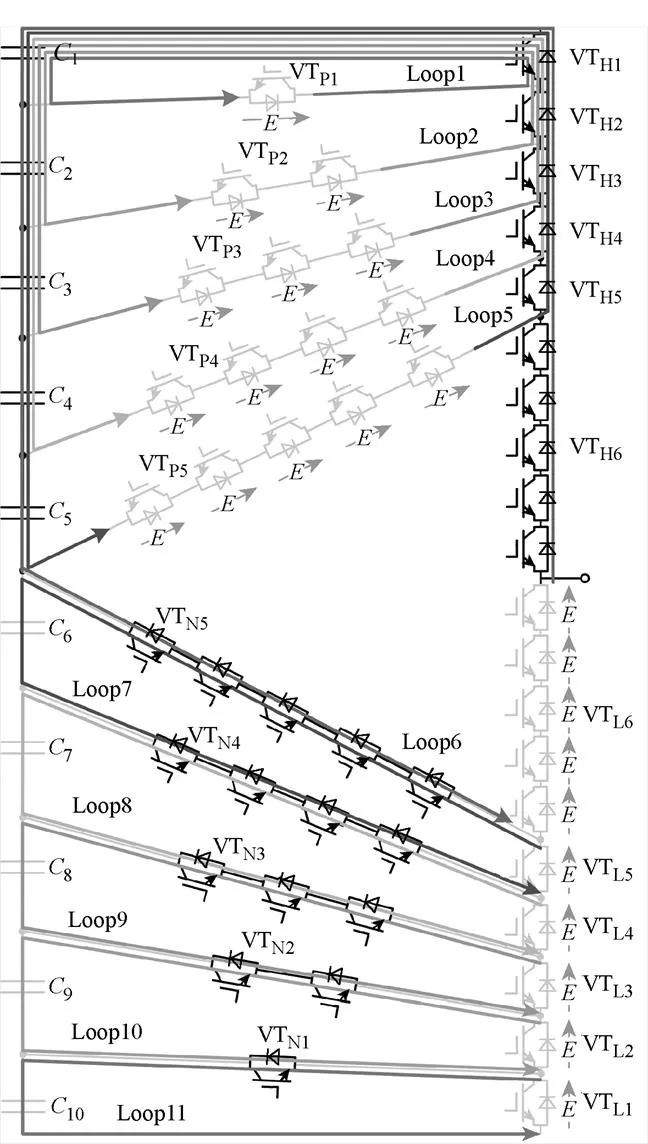
图6 VMC直接钳位机制

同时，从图6可以直观地观察到钳位支路开关管的阻断电压分配。当输出+5电平时，VTP1经回路1被1直接钳位，承受1两端电压；VTP2经回路2被1、2直接钳位，承受1、2两端电压；VTP3经回路3被1～3直接钳位，承受1～3两端电压；VTP4经回路4被1～4直接钳位，承受1～4两端电压；VTP5经回路5被1～5直接钳位，承受1～5两端电压。由于串联开关管的分压作用，此时每个承压开关管承受的电压均为直流侧电容电压。

当VMC输出电平在-4～+4之间时，独立的功率器件的阻断电压仍为直流侧电容电压，而串联开关管中每个开关管承受的电压小于直流侧电容电压。

用相同的方法可以推导得出，VMC多电平变换器在输出任意电平时，都可将输出功率桥臂或钳位支路的独立开关管直接钳位到相对应的直流侧电容上，从而避免了由间接钳位引起的内部开关管静态过电压的问题。同时，每条钳位支路的开关管也直接钳位到直流侧电容两端。偶数电平VMC同样可以分析得出相同的结论，在此不再赘述。VMC中每个开关管最大阻断电压统一为直流侧电容电压，这有助于VMC提升系统电压等级，实现大功率电能变换。同时在工业应用中使用相同等级规格的开关管，有利于批量化生产和降低成本。当然，VMC需要在每个串接开关上并联静态均压电阻，以实现静态电压平衡。

4 VMC和传统多电平拓扑的对比

为评估所提VMC拓扑的优缺点，将VMC与一些目前研究较为广泛的多电平变换器拓扑如NPC、FC、MMC、SMC和ANPC等进行对比。为方便比较，设定所有多电平变换器的开关管和飞跨电容的额定电压都相等且都为一个电平等级。

表2总结了不同单相多电平拓扑输出2+1（为正整数）电平时所需功率器件的数量，包括直流侧电容、飞跨电容、二极管、开关管等。由表2可以看出，对于单相系统而言，相对于NPC和FC总器件数的二次项系数分别为4和2，VMC总器件数的二次项系数降为1，和SMC的总器件数相同。在单相系统中，VMC所用器件数量没有MMC及ANPC有优势。然而，MMC及ANPC的飞跨电容在多相系统中数量会显著增加，同时也会增加控制复杂度。

表2 输出2+1电平时单相变换器器件数量对比

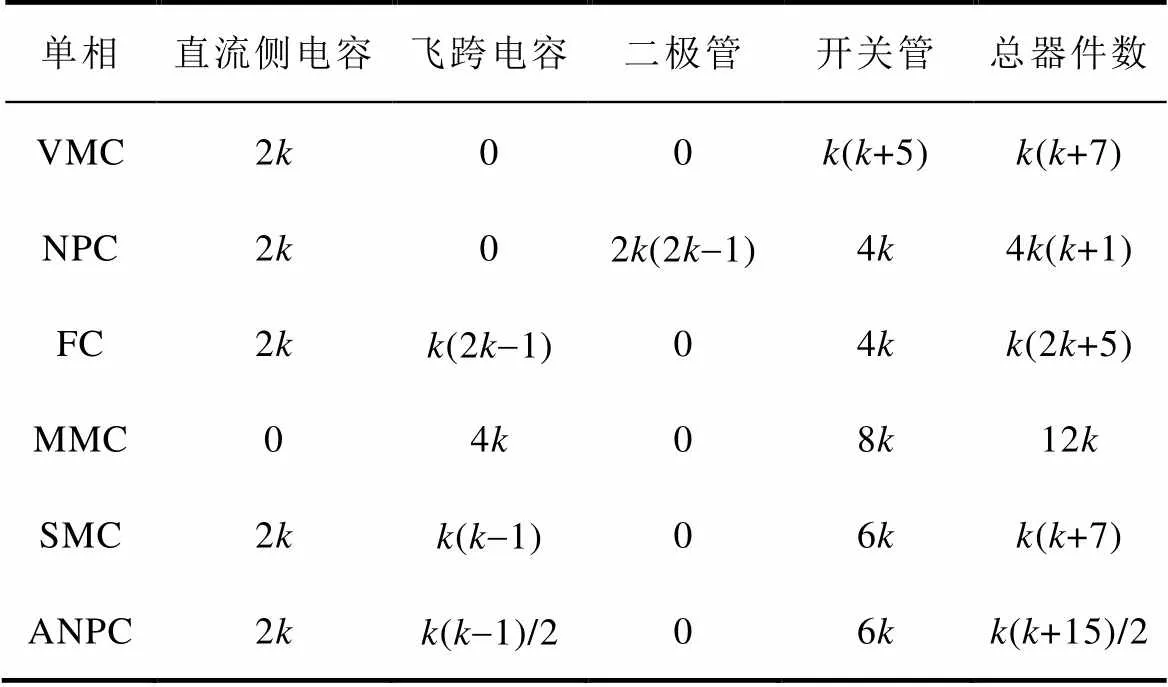
Tab.2 Components of 2k+1 level single-phase converter

图7更直观地展示了三相系统中不同拓扑的器件数量对比，其中，VMC、NPC和FC同时还考虑了偶数电平的情况。结合表2和图7可以看出，相比于NPC和FC，VMC大大减少了器件数量，简化了系统结构。同时VMC没有NPC内管间接钳位的问题，也没有FC复杂的飞跨电容的控制问题。不过，与NPC一样，VMC也面临着直流侧电容电压不平衡的问题[27]。目前一些学者已经提出了一些可行的方法，如可以采用“背靠背”结构[28-29]，添加辅助均压电路[30-31]，以及采用软件控制方法如零序电压注入法[32]和虚拟矢量控制法[33-34]等。值得注意的是，与NPC和FC相比，VMC拓扑在奇数电平向相邻的偶数电平扩展增加一个电平时，其所添加的器件非常少，所以形成了图7中的折线状。针对不同的场合巧妙运用偶数电平VMC，提高了功率器件电压等级选择的灵活性，能够有效降低成本和器件的数量。

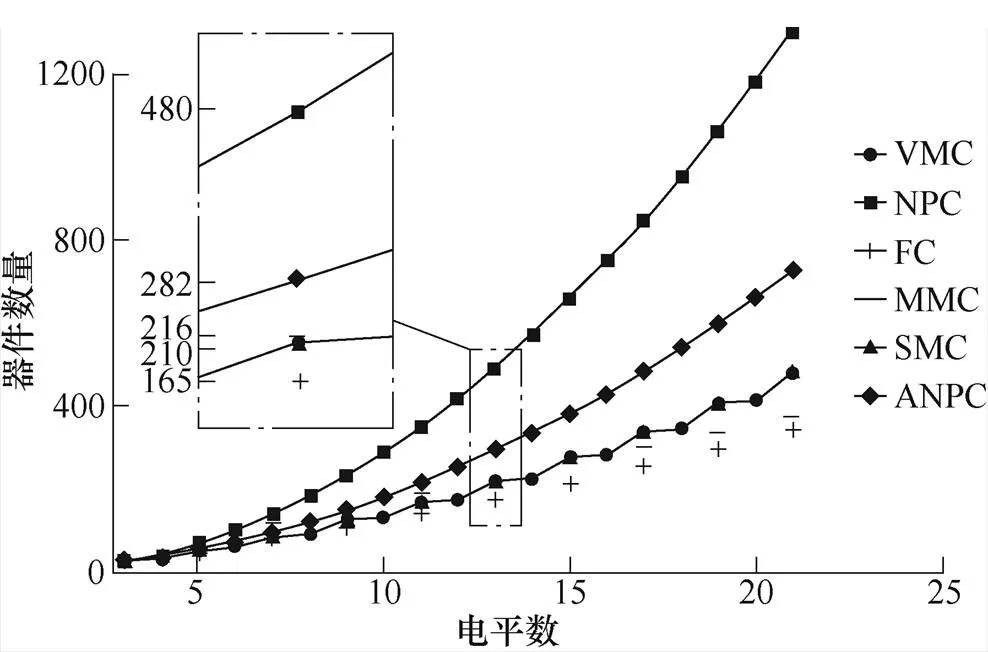
图7 各变换器三相系统所需器件数目

与MMC相比，VMC在三至十三电平范围内在器件数量上比MMC更有优势，如图7中点画线框放大所示，当高于十三电平时，MMC器件数量的优势才显现出来。同时VMC不需要子模块电容和桥臂电感，三相变换器共用直流侧电容，可用较为简单的方法集中实现直流侧电容均压控制。而MMC三相系统中子模块数量较多，子模块电容平衡控制及换流控制也较为复杂。

虽然奇数电平的VMC和SMC、ANPC相比所需器件数量相等或更多，但SMC和ANPC的三相系统中飞跨电容的数量仍然很多，控制相对复杂，而VMC不需要飞跨电容，避免了复杂的飞跨电容平衡控制，减小了变换器体积。

表3根据开关管的电压应力讨论了VMC适用的电压范围。目前常用的IGBT耐压等级有1 200V、1 700V、3 300V、4 500V、6 500V。为实现3kV、6kV、10kV、35kV的电压等级输出，根据逆变器电压转换关系为

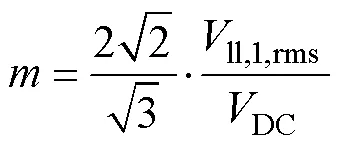
式中，DC为直流母线电压；为调制比；ll,1,rms为输出线电压基波有效值。设定开关管电压等级选取的裕度为1.5～2倍的静态承压，调制比取为0.9，可得不同电平数的多电平变换器所需开关器件电压等级与应用场合电压等级的关系，见表3。

结合表2、图7多电平拓扑的对比，NPC和FC适用于较低电平数如三至五电平，对应表3中3～6kV的电压场合；SMC和ANPC适用于三至七电平，对应3～10kV的电压场合；MMC在电平数较高时能凸显出它的优势，适合于10kV及以上的电压场合。综合器件数量及控制复杂度考虑，VMC应用于在3～35kV电压应用场合较为合适。

表3 多电平变换器器件选择与电压等级的关系

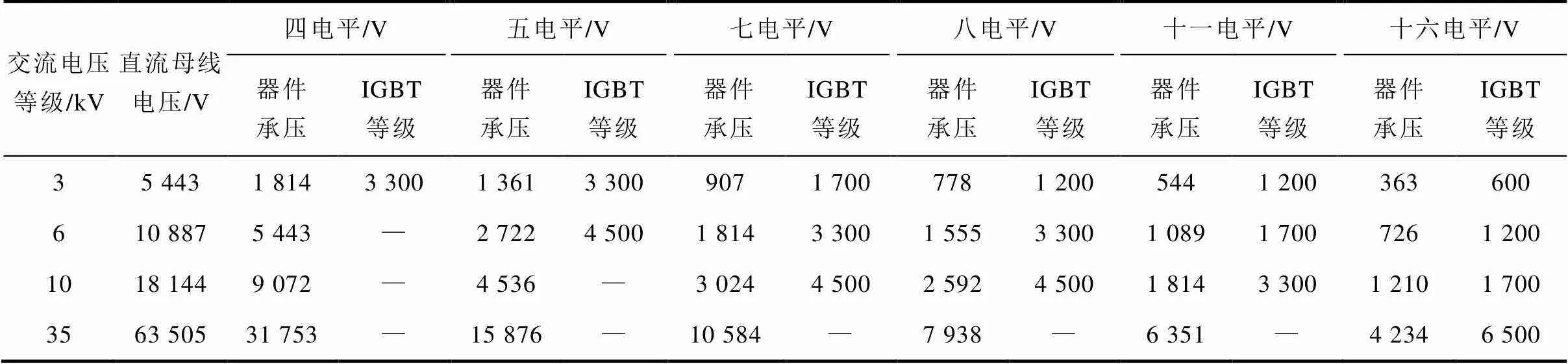
Tab.3 The relationship between devices selection and voltage level

综上所述，VMC拓扑所需器件数量较少，结构简单；无需大量的飞跨电容和电感，简化控制复杂度。针对不同场合巧妙运用偶数电平VMC，增加了器件选择的灵活性，能够有效降低成本和器件数量。相比于现有的其他多电平变换器，VMC在四至十六电平更具有优势，非常适用于中压应用场合，为中压等级的多电平变换器拓扑提供了新思路。

5 仿真和实验验证

为了验证VMC拓扑的可行性，本节给出了仿真和实验结果。在Matlab/Simulink仿真环境下基于多载波SPWM技术分别对七电平和十一电平VMC进行仿真证明，并将文献[27]的谐振开关电容变换电路应用到VMC的直流侧实现直流侧电容电压均衡控制。直流侧电压为18.8kV，七电平VMC中每个电容两端电压为3.13kV，十一电平VMC中每个电容两端电压为1.88kV，调制比为0.86，交流侧负载为300Ω。七电平VMC和十一电平VMC的仿真波形如图8所示。

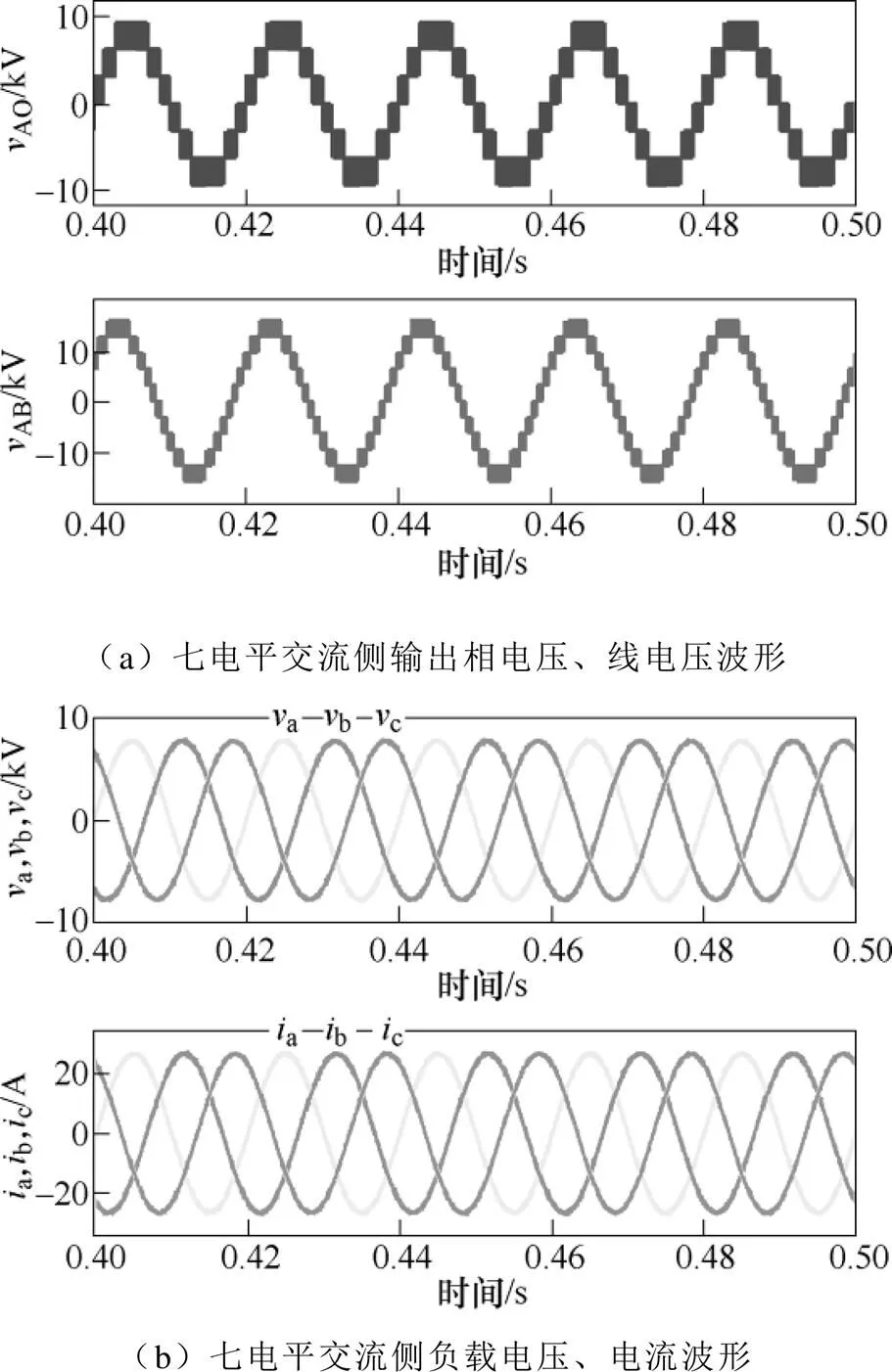
图8 仿真波形

图8a、图8d分别为七电平VMC和十一电平VMC交流侧输出相电压、线电压波形，可以看到，在调制比为0.86的情况下，七电平VMC可以稳定输出七电平台阶的相电压和十一电平台阶的线电压，十一电平VMC可以稳定输出十一电平台阶的相电压和十七电平台阶的线电压。很明显，十一电平VMC的输出波形更接近于正弦波。图8b、图8e为交流侧负载电压、电流波形，负载相电压有效值5 750V，线电压有效值10kV，负载电流有效值20A，三相系统功率可达360kW。这些仿真波形表明，VMC拓扑族能够正常工作，稳定输出交流侧正弦电压和电流。

图8c、图8f分别展示了七电平VMC和十一电平VMC直流侧电容电压波形，可以看出，在10kV电压等级的应用场合下，七电平VMC直流侧电容电压为3.13kV，即七电平VMC中开关管电压应力为3.13kV，可选用4 500V的开关管；十一电平VMC直流侧电容电压为1.88kV，即十一电平VMC中开关管电压应力为1.88kV，可选用3 300V的开关管。这两款开关管都是较为常用的IGBT电压等级。这些仿真波形表明，VMC拓扑族可选用商用主流IGBT来实现10kV电压等级的电能变换。

图8g为十一电平VMC上半桥臂开关管两端的电压波形。可以看出，功率桥臂上的开关管总是能被直接钳位到直流侧电容两端，开关管承压为直流侧电容电压。对于钳位支路的开关管，当输出最高电平+5时，钳位支路的每个开关管都承受直流侧电容电压，随着电平数的降低，串联开关管承受的电压呈阶梯状降低。例如，当输出+4电平时，开关管VTP21和VTP22共同承担直流侧电容2两端的电压，每个开关管承受直流侧电容电压的一半；开关管VTP31、VTP32、VTP33共同承担直流侧电容2、3的电压，每个开关管承受直流侧电容电压的三分之二；其他钳位支路的开关管承压与此类似。可见每个开关管的最大阻断电压都为。

此外，本文搭建了380V/7.2kW三相七电平VMC的缩比实验样机。实验中，系统额定直流电压为720V，由6个独立直流电源供电，每个直流母线电容两端的电压为120V。

相电压、线电压及相电流实验波形如图9所示。图9a为变换器三相输出相电压的波形，变换器稳定输出七电平相电压，且三相互差120°，与仿真结果相一致。每个电平等级为120V，多电平波形的各电平等级清晰。

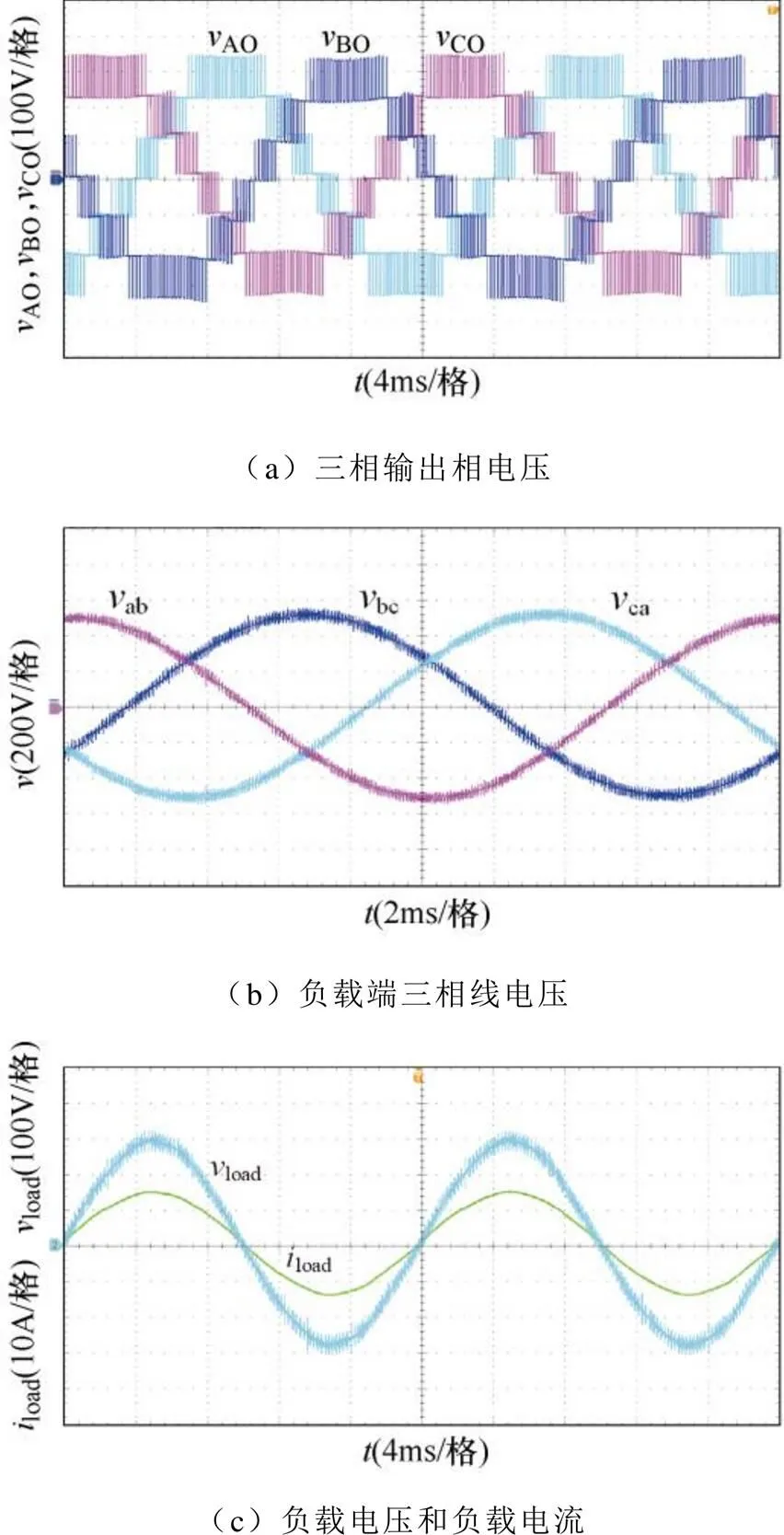
图9 相电压、线电压及相电流实验波形

通过滤波器将高频谐波滤除，得到质量良好的负载端波形，如图9b、图9c所示。负载端线电压有效值为380V，负载电流的最大值约为15A，三相功率可达7.2kW。由图9可以看出，VMC在现有开关状态和调制方式下运行良好，不依赖飞跨电容即可实现多电平的平稳输出。负载电流快速傅里叶变换（Fast Fourier Transform, FFT）分析如图10所示，采用较小的滤波器，其谐波含量也较低。

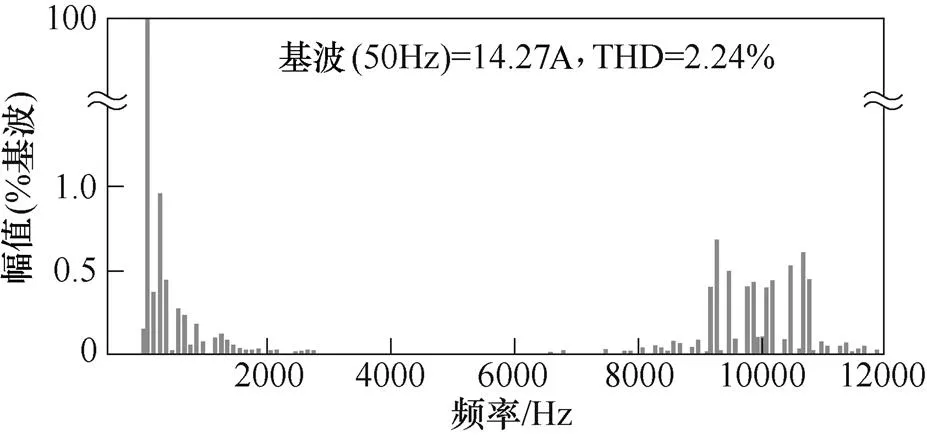
图10 负载电流FFT分析

图11展示了开关管两端的电压波形，稳态下每个开关管承受的最大电压都为直流侧电容电压120V。当输出最高电平时，钳位支路的开关管承压都为120V，当输出+2电平时，VTP21和VTP22需承受直流侧电容2两端的电压，每个开关管承受压降60V；VTP31、VTP32和VTP33需承受直流侧2、3两个电容电压，每个开关管承受压降80V。当输出+电平时，VTP31、VTP32和VTP33需承受直流侧3电容电压，每个开关管承受压降40V。

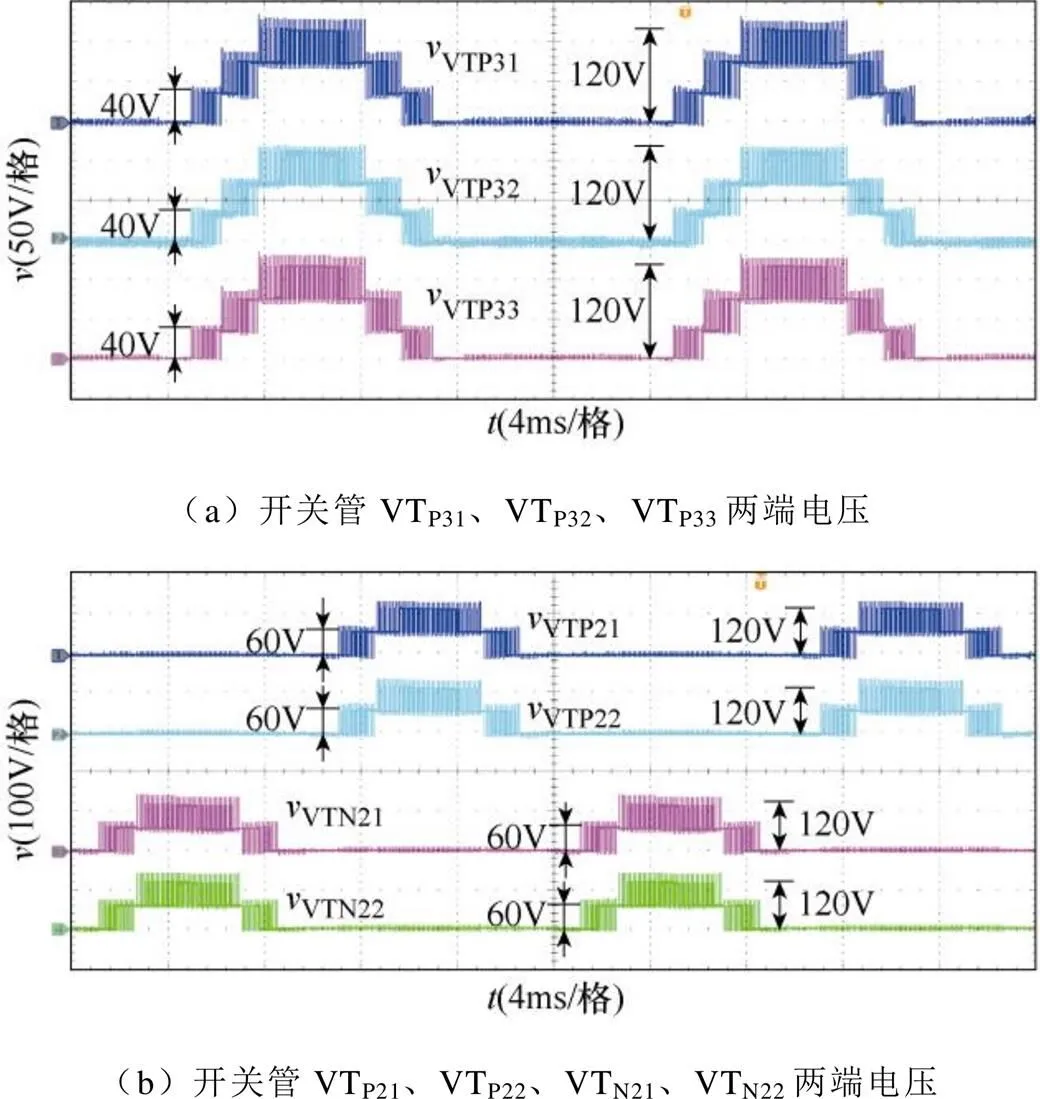
图11 开关管两端的电压波形

综上，VMC多电平变换器能够输出质量较好的正弦电流及正弦电压，实验结果较好地验证了V形钳位多电平变换器拓扑及控制方法的可行性。

6 结论

本文为V形钳位多电平变换器拓扑族在中压大功率电能变换领域的应用提供了理论基础和技术指导，介绍了VMC拓扑的拓展方式、一般形式及演化类型，并对VMC拓扑的主要特性进行了详细研究。仿真和实验结果验证了V形钳位多电平变换器拓扑及控制方法的可行性。主要结论如下：

1）VMC拓扑拓展方式简单，奇数电平扩展到相邻偶数电平时，只需增加一个直流侧电容和两个输出功率桥臂开关管。针对不同场合巧妙运用偶数电平VMC，能够增加器件选择的灵活性，并有效地减少器件数量和降低成本。根据零电平通路变形规则，可得到二极管钳位型、上钳位型、下钳位型、中点钳位型四种VMC演化类型。

2）VMC无间接钳位问题，每个开关管都被直接钳位在直流侧电容两端，且每个开关管最大承受电压均为直流侧电容电压。这有助于VMC提升系统电压等级，实现大功率电能变换，且有利于工业应用中的批量化生产和降低成本。

3）VMC拓扑所需器件数量较少、结构简单；无需大量的飞跨电容和电感，体积可以大大减小，同时控制简单易行。相比于现有的其他多电平变换器，VMC在四至十七电平更能凸显VMC的器件数量少及控制简单的优势。就目前市场的功率器件电压等级而言，非常适用于3～35kV中压应用场合。

综上所述，V形钳位多电平变换器在中压大功率电能变换领域具有广阔的应用前景和发展潜力。

[1] Rodriguez J, Lai J S, Peng Fangzheng. Multilevel inverters: a survey of topologies, controls, and appli- cations[J]. IEEE Transactions on Industrial Electro- nics, 2002, 49(4): 724-738.

[2] Kouro S, Malinowski M, Gopakumar K, et al. Recent advances and industrial applications of multilevel converters[J]. IEEE Transactions on Industrial Elec- tronics, 2010, 57(8): 2553-2580.

[3] Lai J S, Peng Fangzheng. Multilevel converters-a new breed of power converters[J]. IEEE Transactions on Industry Applications, 1996, 32(3): 509-517.

[4] 张雪垠, 徐永海, 李卫国, 等. 中压模块化多电平换流器降低开关频率的锯齿载波最近电平-脉宽调制方法[J]. 电工技术学报, 2020, 35(8): 1716-1727.

Zhang Xueyin, Xu Yonghai, Li Weiguo, et al. A reduced-switching frequency NL-PWM method based on sawtooth carrier for medium voltage modular multilevel converter[J]. Transactions of China Elec- trotechnical Society, 2020, 35(8): 1716-1727.

[5] 张亮, 陈国栋, 朱纪洪, 等. H桥级联型多电平高压调速系统低速畸变补偿控制技术[J]. 电工技术学报, 2017, 32(22): 13-21.

Zhang Liang, Chen Guodong, Zhu Jihong, et al. Distortion compensation control designed for H- bridge cascade multilevel converter under low speed condition[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 13-21.

[6] Vodyakho O, Mi C C. Three-level inverter-based shunt active power filter in three-phase three-wire and four-wire systems[J]. IEEE Transactions on Power Electronics, 2009, 24(5): 1350-1363.

[7] 杨用春, 肖湘宁, 郭世枭, 等. 基于模块化多电平变流器的统一电能质量调节器工程实验装置研究[J]. 电工技术学报, 2018, 33(16): 3743-3755.

Yang Yongchun, Xiao Xiangning, Guo Shixiao, et al. Research of unified power quality conditioner engineering experiment device based on modular multilevel converter[J]. Transactions of China Elec- trotechnical Society, 2018, 33(16): 3743-3755.

[8] Alepuz S, Busquets-Monge S, Bordonau J, et al. Interfacing renewable energy sources to the utility grid using a three-level inverter[J]. IEEE Transactions on Industrial Electronics, 2006, 53(5): 1504-1511.

[9] Bhagwat P M, Stefanovic V R. Generalized structure of a multilevel PWM inverter[J]. IEEE Transactions on Industry Applications, 1983, IA-19(6): 1057- 1069.

[10] 王琛琛, 李永东. 多电平变换器拓扑关系及新型拓扑[J]. 电工技术学报, 2011, 26(1): 92-99.

Wang Chenchen, Li Yongdong. Multilevel converter topologies and two novel topologies[J]. Transactions of China Electrotechnical Society, 2011, 26(1): 92- 99.

[11] Choi N S, Cho J G, Cho G H. A general circuit topology of multilevel inverter[C]//22nd Annual IEEE Power Electronics Specialists Conference, Cambridge, MA, USA, 1991: 96-103.

[12] Nabae A, Takahashi I, Akagi H. A new neutral- point-clamped PWM inverter[J]. IEEE Transactions on Industry Applications, 1981, IA-17(5): 518-523.

[13] Meynard T A, Foch H, Thomas P, et al. Multicell converters: basic concepts and industry applica- tions[J]. IEEE Transactions on Industrial Electronics, 2002, 49(5): 955-964.

[14] Shukla A, Ghosh A, Joshi A. Natural balancing of flying capacitor voltages in multicell inverter under PD carrier-based PWM[J]. IEEE Transactions on Power Electronics, 2011, 26(6): 1682-1693.

[15] 王昕, 王琛琛, 顾长彬. 级联H桥整流器稳定运行区域和直流侧电压平衡策略的调节能力分析[J]. 电工技术学报, 2019, 34(14): 2970-2979.

Wang Xin, Wang Chenchen, Gu Changbin. Analysis about steady-state operating region and regulation capacity of voltage balance strategy for cascaded H- bridge rectifier[J]. Transactions of China Electro- technical Society, 2019, 34(14): 2970-2979.

[16] Mariethoz, Sébastien. Systematic design of high- performance hybrid cascaded multilevel inverters with active voltage balance and minimum switching losses[J]. IEEE Transactions on Power Electronics, 2013, 28(7): 3100-3113.

[17] 尹太元, 王跃, 段国朝, 等. 基于零直流电压控制的混合型MMC-HVDC直流短路故障穿越策略[J]. 电工技术学报, 2019, 34(增刊1): 343-351.

Yin Taiyuan, Wang Yue, Duan Guozhao, et al. Zero DC voltage control based DC fault ride-through strategy for hybrid modular multilevel converter in HVDC[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 343-351.

[18] Deng Yi, Wang Yebin, Teo K H, et al. Optimized control of the modular multilevel converter based on space vector modulation[J]. IEEE Transactions on Power Electronics, 2018, 33(7): 5697-5711.

[19] Gateau G, Meynard T A, Foch H. Stacked multicell converter (SMC): properties and design[C]//2001 IEEE 32nd Annual Power Electronics Specialists Conference, Vancouver, BC, 2001, 3: 1583-1588.

[20] Barbosa P, Steimer P, Meysenc L, et al. Active neutral-point-clamped multilevel converters[C]//2005 IEEE 36th Power Electronics Specialists Conference, Recife, 2005: 2296-2301.

[21] Pulikanti S R, Konstantinou G S, Agelidis V G. Generalisation of flying capacitor-based active- neutralpoint- clamped multilevel converter using voltage-level modulation[J]. IET Power Electronics, 2012, 5(4): 456-466.

[22] Sheng Weihui, Ge Qiongxuan. A novel seven-level ANPC converter topology and its commutating strategies[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 7496-7509.

[23] Zheng Trillion Q, Xue Yao, Yuan Lutian, et al. V- clamp multilevel converter-a new type multilevel converter with common DC-link capacitors[R]. In Proceedings of the Jing-Jin-Ji High-End Forum for Power Electronics, Beijing, China, 2019.

[24] Xue Yao, Yang Xiaofeng, Yuan Lutian, et al. Operation and control of a seven-level V-clamp multilevel converter[J]. Energies, 2019, 12(24): 4761.

[25] Yuan Xiaoming, Orglmeister G, Barbi I. ARCPI resonant snubber for the neutral-point-clamped inver- ter[J]. IEEE Transactions on Industry Applications, 2000, 36(2): 586-595.

[26] Yuan Xiaoming, Barbi I. Fundamentals of a new diode clamping multilevel inverter[J]. IEEE Transa- ctions on Power Electronics, 2000, 15(4): 711-718.

[27] Busquets-Monge S, Ruderman A. Carrier-based PWM strategies for the comprehensive capacitor voltage balance of multilevel multileg diode-clamped con- verters[C]//2010 IEEE International Symposium on Industrial Electronics, Bari, 2010: 688-693.

[28] Peng Fangzheng, Lai J S, McKeever J, et al. A multilevel voltage-source converter system with balanced DC voltages[C]//Proceedings of Power Electronics Specialist Conference, Atlanta, GA, USA, 1995, 2: 1144-1150.

[29] Pan Zhiguo, Peng Fangzheng. A sinusoidal PWM method with voltage balancing capability for diode- clamped five-level converters[J]. IEEE Transactions on Industry Applications, 2009, 45(3): 1028-1034.

[30] Sano K, Fujita H. Voltage-balancing circuit based on a resonant switched-capacitor converter for multilevel inverters[J]. IEEE Transactions on Industry Appli- cations, 2008, 44(6): 1768-1776.

[31] Shu Zeliang, He Xiaoqiong, Wang Zhiyong, et al. Voltage balancing approaches for diode-clamped multilevel converters using auxiliary capacitor-based circuits[J]. IEEE Transactions on Power Electronics, 2013, 28(5): 2111-2124.

[32] 张建忠, 胡路才, 徐帅. 一种零序电压注入的T型三电平逆变器中点电位平衡控制方法[J]. 电工技术学报, 2020, 35(4): 807-816.

Zhang Jianzhong, Hu Lucai, Xu Shuai. Neutral potential balance control method of T-type three-level inverter with zero-sequence voltage injection[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 807-816.

[33] Busquets-Monge S, Alepuz S, Rocabert J, et al. Pulsewidth modulations for the comprehensive capacitor voltage balance of n-level three-leg diode- clamped converters[J]. IEEE Transactions on Power Electronics, 2009, 24(5): 1364-1375.

[34] Wang Kui, Zheng Zedong, Li Yongdong. A novel carrier-overlapped PWM method for four-level neutral-point clamped converters[J]. IEEE Transa- ctions on Power Electronics, 2019, 34(1): 7-12.

V-Clamp Multilevel Converters Suitable for Medium-Voltage Fields

（College of Electrical Engineering Beijing Jiaotong University Beijing 100044 China）

Multilevel converter has been widely used in the medium/high-voltage high-power conversion fields. This paper proposes a new family of topologies named V-clamp multilevel converters (VMCs), which can achieve medium-voltage high-power conversion by a small number of devices. Besides, without flying capacitors employed in the phase legs, the control of the VMC is much easier and simpler. This paper reveals the composition of the VMC topology family, including the expansion method, general form, and evolution type. On this basis, this paper investigates the working principle and control method of VMCs, and analyzes the direct clamping mechanism and blocking voltage distribution. Compared with the existing multilevel converters, the VMC is more suitable for medium-voltage applications. The simulation and experimental results verify the feasibility of the VMC topology family and control method, and further prove the correctness of the theoretical analysis in this paper.

Multilevel converters, power conversion, DC-link capacitors, direct clamping, V-clamp

10.19595/j.cnki.1000-6753.tces.L90365

TM46

原露恬 女，1995年生，硕士研究生，研究方向为大功率电力电子变换器技术。E-mail: 18121533@bjtu.edu.cn

郑琼林 男，1964年生，教授，博士生导师，研究方向为轨道交通牵引供电与交流传动、电力系统中的电力电子技术、电力有源滤波与电能质量等。E-mail: tqzheng@bjtu.edu.cn（通信作者）

2020-07-10

2020-11-16

国家自然科学基金重点资助项目（51737001）。

（编辑 陈 诚）