低应力高电平开关电容逆变器及其调制策略

王要强 张亨泰 赖锦木 王克文 梁 军

低应力高电平开关电容逆变器及其调制策略

王要强1,2张亨泰1,2赖锦木1,2王克文1,2梁 军1,3

（1. 郑州大学电气工程学院 郑州 450001 2. 河南省电力电子与电能系统工程技术研究中心 郑州 450001 3. 卡迪夫大学 卡迪夫 CF243AA）

为了提高可再生能源发电系统中逆变器的升压能力并改善输出电能质量，该文提出一种低应力高电平开关电容逆变器。所提拓扑使用1个直流电源、3个电容和15个开关器件实现4倍电压增益和十七电平交流电压输出。与其他拓扑相比，所提逆变器能以较少的开关器件产生更多的电平，有效地降低了逆变器的输出谐波含量；无需后端H桥即可实现逆变过程，有效地降低了开关器件的电压应力。此外，所提逆变器的电容电压纹波小，且电容电压自平衡的优点简化了控制器的复杂度。该文详细给出所提逆变器的拓扑结构、工作机理与调制策略，分析电容电压纹波计算，并与其他类似拓扑结构进行对比，最后通过实验证明了所提逆变器的可行性和理论分析的正确性。

多电平逆变器 开关电容 低应力 高输出电平 电容电压自平衡

0 引言

伴随着经济与社会的发展，环境和能源问题日渐突出。煤炭、石油等化石能源的开采和消耗是不可持续的，且会导致气候变化、环境污染、生态破坏并可能危害人体健康。因而能够化解以上问题的可再生能源被广泛应用，世界各国对于可再生能源的需求也与日俱增[1]。可再生能源发电，如光伏发电等，成为日益重要的发电方式[2]。光伏电池组件产生的直流电需要通过逆变器为负载供电或接入交流电网，因此高性能的逆变器在光伏发电系统中至关重要[3]。

相较于二电平逆变器，多电平逆变器电磁干扰小，能够在承受更高电压的同时输出更高质量的正弦波形[4]。传统的多电平逆变器主要包括级联H桥型、二极管钳位型和飞跨电容型[5]。级联H桥型多电平逆变器将各直流电源分别供电的H桥单元串联，输出多电平的交流电压波形。二极管钳位型多电平逆变器用二极管来隔断直流电源；类似地，飞跨电容型逆变器用大电容来阻断电压[6]。但是传统多电平逆变器使用了大量的直流电源、二极管和电容等器件，飞跨电容型与二极管钳位型逆变器的直流电容还存在均压问题[7]。此外，光伏发电单元的输出电压通常不能满足并网要求，光照、温度、阴影等因素可能导致最大功率点电压降低[8]，而传统的多电平逆变器并不具备升压功能。为了解决上述问题，Z源、模块化多电平和开关电容为代表的新型多电平逆变器正快速发展[9-11]。开关电容多电平逆变器通过开关的导通与关断实现电容的串并联与充放电，能够以较少的器件输出高电平，开关承受的电压应力低且能够实现电容电压自平衡[12]。

文献[13]提出的是一种典型的使用H桥的开关电容型多电平逆变器拓扑，它使用阶梯形的升压单元产生高电平，通过H桥控制输出电平的正负。文献[14]中的开关电容多电平逆变器拓扑直接将电源和电容放在H桥中然后串联，通过改变电容数量调整输出电平。该拓扑使用多个H桥以降低开关的电压应力，调制也比较简单；但是它需要使用辅助充电回路以降低尖峰电流。以上两种拓扑可以使用直流电源为每个电容分别充电，不用考虑电容电压平衡问题；但是使用了大量的器件，且在拓展模块时新增加的电容电压纹波较大，限制了输出电平数量。文献[15-17]提出了一系列X型开关电容多电平逆变器拓扑，其特点是将直流电源与电容的正负极交叉连接实现串联与并联，该类拓扑能够使用较少器件输出较多电平，并实现电容电压自平衡；然而该类拓扑无法降低开关的电压应力，也没有带感性负载的能力。文献[18-19]提出的九电平开关电容逆变器使用直流电源和电容串联为后级电容充电，具备电容电压自平衡功能，实现了4倍电压增益和带感性负载能力，拓展时输出电平数呈指数增长。然而，该拓扑虽然降低了总电压应力，但它仍有两个开关需要承受等于峰值输出电压的应力。文献[20-21]提出的拓扑使用了多个直流电源以提高输出电平，降低开关的电压应力；在输出较高的电平时，其使用的器件数更少。由于使用直流电源直接为单个电容充电，该拓扑也不需要考虑电容电压平衡问题。但是这种拓扑对直流电源的数量和不同直流电源的输出电压有更多的要求，结构也更为复杂。

本文提出了一种低应力高电平开关电容逆变器。相比于现有拓扑，本文所提拓扑能够使用更少的器件输出更多电平、降低开关的电压应力、具备电容电压自平衡和带感性负载能力。本文详细介绍了所提开关电容多电平逆变器的拓扑结构、调制策略、电容电压自平衡与纹波分析，通过与其他类似拓扑对比以突出该拓扑的优势，最后通过实验验证了该逆变器的可行性和正确性。

1 逆变器拓扑结构与工作机理

1.1 拓扑结构

合适的电路设计可以使逆变器实现尽可能多的功能。本文所提的多电平逆变器的升压单元结构如图1所示，它使用一个直流电源为电容1和2充电；开关S3和S5同时导通和关断，并与开关S4互补导通，实现电容1和2串联与并联的切换；开关S1和互补导通的开关对S2、S6实现直流电源与两个电容间并联和串联的切换。通过控制充放电过程，该升压单元可以实现两个电容的状态完全一致，解决了电容电压平衡问题。需要指出的是，这里的直流源可以是输出直流电压的光伏组件或燃料电池等。

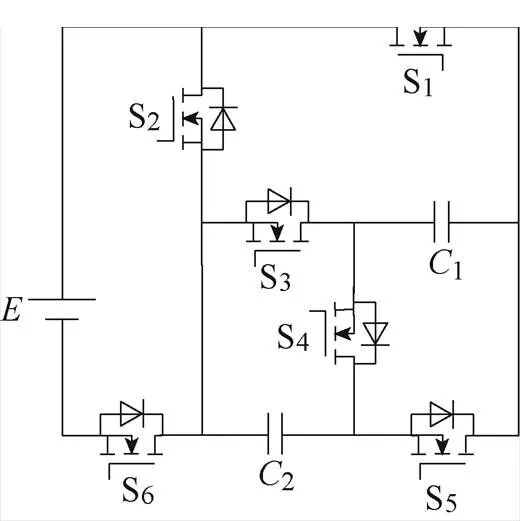
图1 所提的升压单元结构

在所提升压单元结构的基础上，进一步提出了低应力十七电平开关电容逆变器，如图2所示。该逆变器拓扑旨在使用尽量少的器件实现尽可能高的输出电平，提高其输出电能质量[22]。所提逆变器拓扑使用5个开关S7～S11组成的“工”字形结构将升压单元和电容3连接起来；使用开关S12、S13和S14、S15分别组成的两个“半桥”代替H桥来转换输出电平的极性。这样的设计既实现了升压单元与电容3的并联充电和串联放电，又降低了开关的电压应力。

本文所提的逆变器拓扑包含了1个直流电源、3个电容和15个开关（14个带反向二极管的开关器件（如MOSFET）和1个不带反向二极管的开关器件）。该拓扑能够通过升压单元与电容3的串联放电实现最高十七电平的输出阶梯波，具有4倍电压增益。升压单元中所有开关承受的最大电压应力均等于直流源的电压值，“工”字形结构与两个“半桥”中的开关承受的最大电压应力均为2。所有开关承受的总电压应力为22.5。

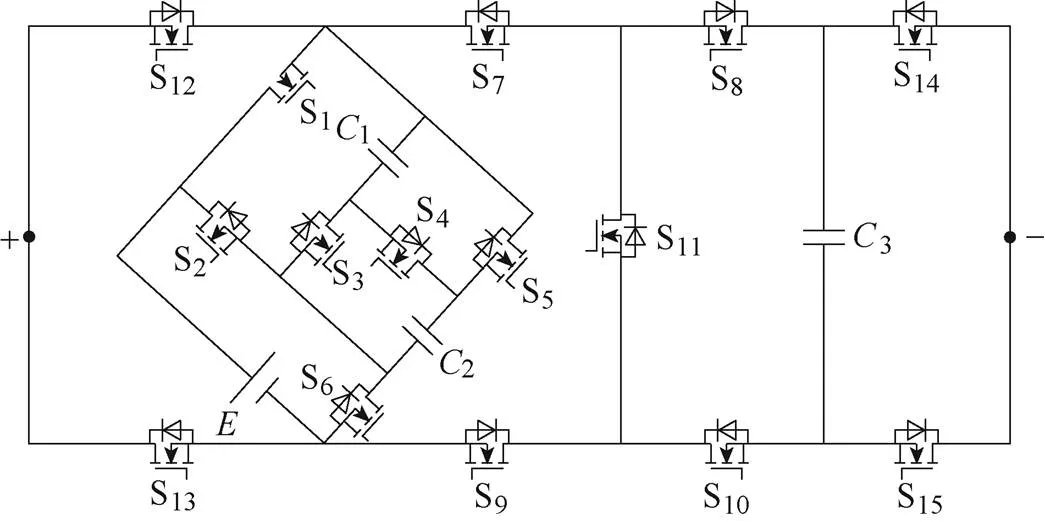
图2 所提的十七电平开关电容逆变器

1.2 工作机理

图3给出了输出0电平和正电平时逆变器在不同工作状态下的运行状态。符号“+”与“-”代表接入负载的正、负极，逆变器输出电压用表示；实线代表放电回路；虚线代表续流回路，箭头则代表其方向。

工作状态1，如图3a所示：升压单元中开关S4导通，电容1和2串联；开关S1和S6导通，直流电源与电容并联，为电容充电。“工”字形开关结构中开关S9和S10导通，升压单元单独放电；输出端中开关S13和S15导通，逆变器输出电压=0。

工作状态2，如图3b所示：升压单元中开关S3和S5导通，电容1和2并联；开关S6导通，直流电源与电容不连接。“工”字形开关结构中开关S9和S10导通，升压单元单独放电；输出端中开关S12和S15导通，逆变器输出电压=0.5。

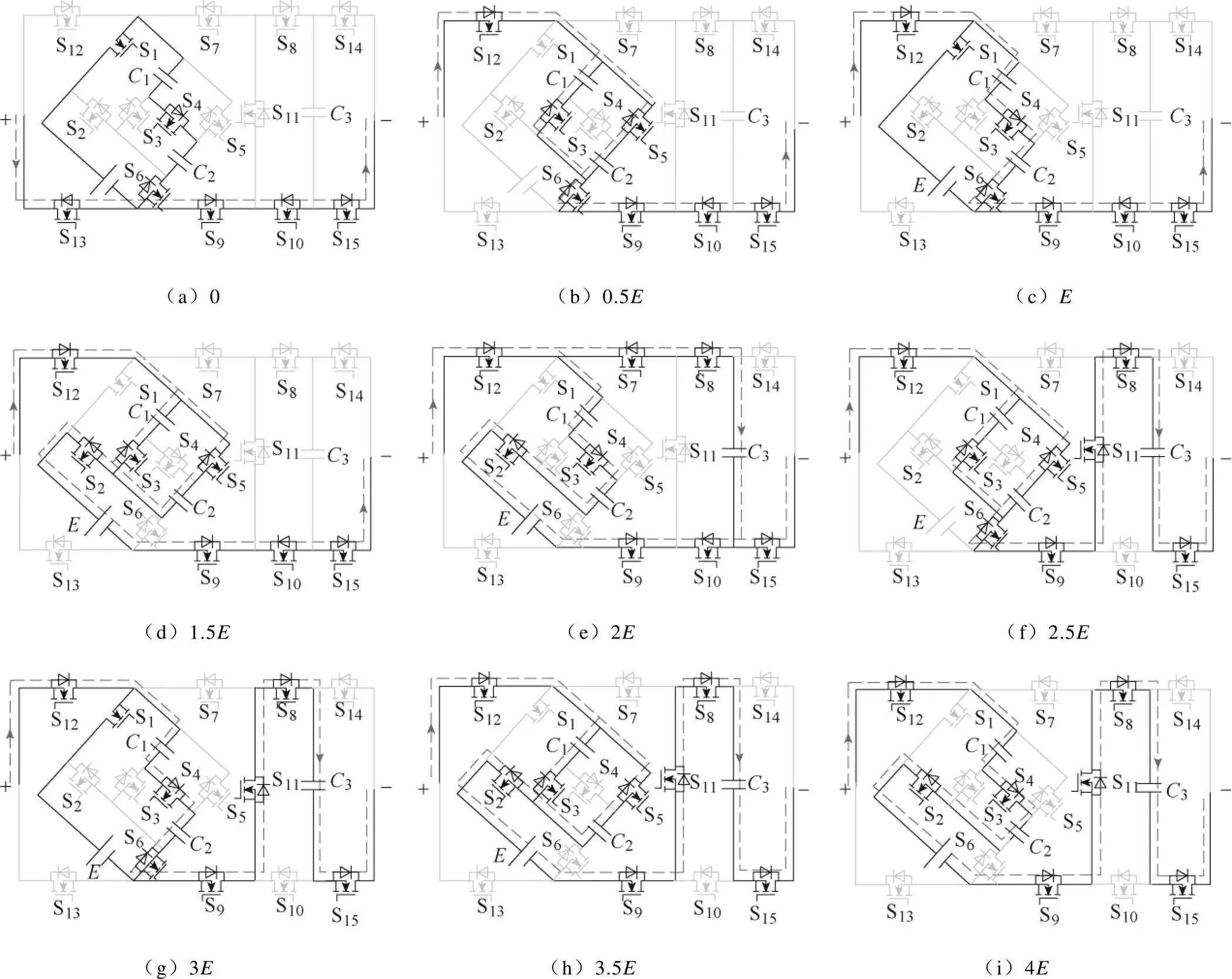
图3 所提拓扑在正半周期运行时的工作状态

工作状态3，如图3c所示：升压单元中开关S4导通，电容1和2串联；开关S1和S6导通，直流电源与电容并联，为电容充电。开关结构中开关S9和S10导通，升压单元单独放电；输出端中开关S12和S15导通，逆变器输出电压=。

工作状态4，如图3d所示：升压单元中开关S3和S5导通，电容1和2并联；开关S2导通，直流电源与电容串联放电。开关S9和S10导通，升压单元单独放电；开关S12和S15导通，输出电压=1.5。

工作状态5，如图3e所示：升压单元中开关S4导通，电容1和2串联；开关S2导通，直流电源与电容串联。开关S7、S8、S9和S10共同导通，升压单元为电容3充电；开关S12和S15导通，输出电压=2。

工作状态6，如图3f所示：升压单元中开关S3和S5导通，电容1和2并联；开关S6导通，直流电源与两个电容不连接。开关S8、S9和S11导通，升压单元与电容3串联放电；开关S12和S15导通，输出电压=2.5。

工作状态7，如图3g所示：升压单元中开关S4导通，电容1和2串联；开关S1和S6导通，直流电源与电容并联，为电容充电。开关S8、S9和S11导通，升压单元与电容3串联放电；开关S12和S15导通，输出电压=3。

工作状态8，如图3h所示：升压单元中开关S3和S5导通，电容1和2并联；开关S2导通，直流电源与电容串联。开关S8、S9和S11导通，升压单元与电容3串联放电；开关S12和S15导通，输出电压=3.5。

工作状态9，如图3i所示：升压单元中开关S4导通，电容1和2串联；开关S2导通，直流电源与电容串联。开关S8、S9和S11导通，升压单元与电容3串联放电；开关S12和S15导通，输出电压=4。

从拓扑各个工作状态的导通回路可以看出，续流回路通过了电源、电容以及开关的反向并联二极管，与正向电流流通路径完全相同。各个工作状态均具备相应的续流回路，表明该逆变器具备带感性负载的能力。

表1 所提拓扑中开关和电容在正半周期运行时的工作状态

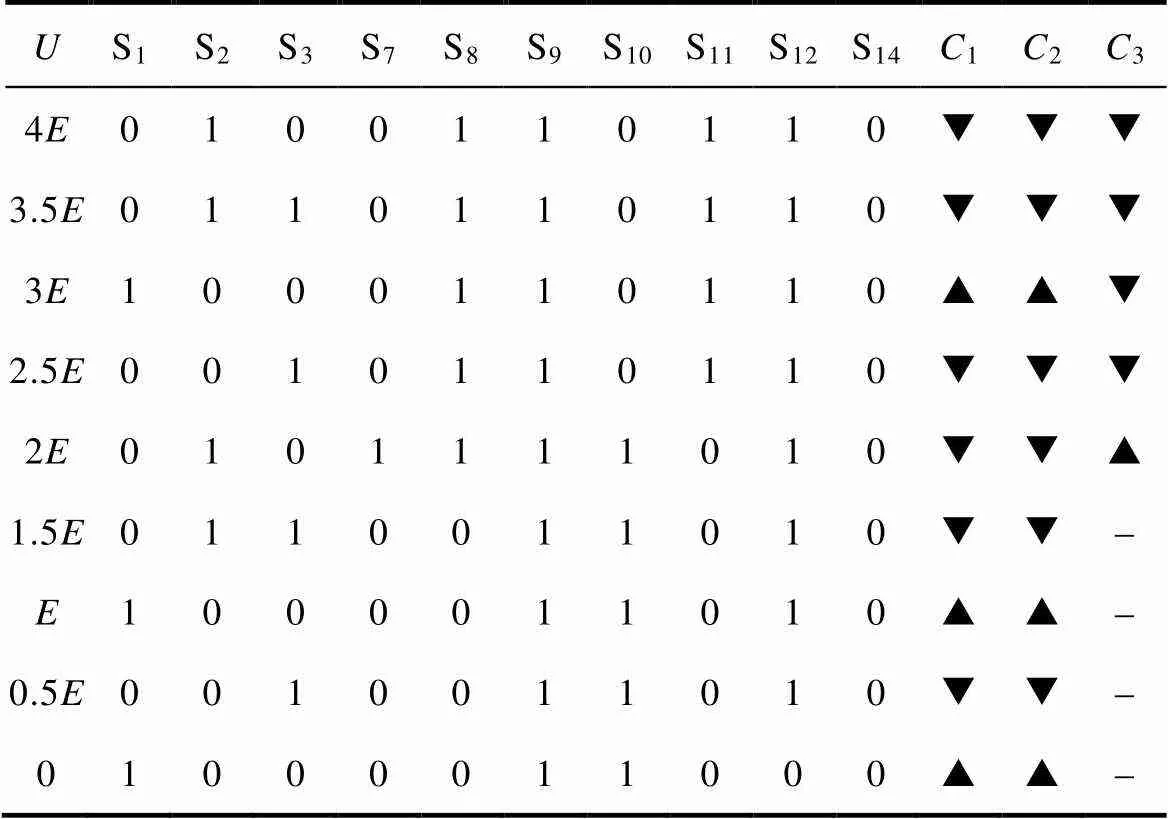
Tab.1 Operating states of switches and capacitors for the proposed inverter in positive half cycle

1.3 拓展方式

本文所提的逆变器可以通过级联拓展方式实现更高的输出电平。该方式以整个逆变器拓扑为基本单元，将不同单元首尾串联起来。级联拓展方式操作简便并能够保持开关应力不变，还可以使用不对称电源获得更高的输出电平。但是，它的缺点是需要使用多个直流电源。

为了最大程度上简化结构，本文提出了一种模块化拓展方式，通过增加可拓展模块来提高输出电平。所提拓扑的模块化拓展方式如图4所示，升压单元同时为所有可拓展模块充电，各模块与升压单元串联放电以增加输出电平。在模块化拓展结构中，每增加一个模块，将增加8个输出电平。输出电平数与模块数的关系为

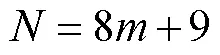
式中，N为输出电平数；m为模块数。这种拓展方式不仅可以保持级联拓展方式的优点，而且只需要一个直流电源。此外，相邻模块中的电容可以并联放电，进一步降低了电容的电压纹波。

2 调制策略

用于开关电容多电平逆变器的脉宽调制（Pulse Width Modulation, PWM）方法主要有载波调制PWM控制法、消除特定谐波PWM控制法和空间矢量PWM控制法[23]。其中，空间矢量法适用于较低输出电平的逆变器，而消除特定谐波法的计算过程过于复杂[24]。本文采用实现简单且消除谐波效果好的载波同相层叠PWM控制法对提出的拓扑进行调制，其原理波形如图5所示。

在载波同相层叠PWM控制技术中，首先将多个相同频率、相位和幅值的三角载波在横轴上下连续层叠后与正弦调制波比较；再用正弦波瞬时值大于三角波的部分产生输出电压的PWM脉冲，小于三角波的部分产生零脉冲；然后将得到的原始脉冲波形通过逻辑组合得到开关的控制信号波形，使该控制信号能够驱动开关实现逆变器的不同工作状态，最终逆变器输出理想的目标波形。提出的逆变器拓扑输出电平数较多，通过正半周期的8路PWM波形来描述调制策略的原理，且能够对应第1节拓扑在正半周期的状态变化。如图5a所示，8路幅值为c、频率为c的三角载波在横轴上方连续层叠。幅值为、频率为的正弦调制波与三角载波比较后得到图5b中的8路原始PWM脉冲波形，从上至下依次为1～8。调制策略中的调制比由调制波幅值和载波幅值确定，即

图5 载波同相层叠PWM控制法的原理波形

在设计的调制方案中，调制比为0.9。调制波与载波的比较结果1～8在各个时间段内根据设定的逻辑关系组合成图5c中各开关的控制信号波形。其中，高电平代表开通；低电平代表关断。各开关的控制信号能够驱动开关实现表1中的状态变化。在正半周期内，表1中，各开关与8路原始PWM脉冲波形的逻辑关系如下

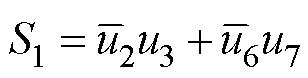
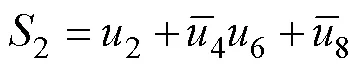
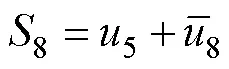
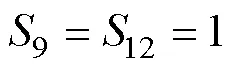
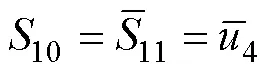
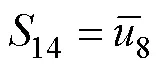
利用该逻辑关系和原始PWM脉冲波形即可得到正半周期内开关的控制信号波形。需要指出的是，需要整个周期的波形驱动开关才可以得到逆变器的目标输出波形。

3 电容电压分析与纹波计算

3.1 电容电压自平衡

电容电压自平衡是开关电容多电平逆变器正常工作的前提，也是其相较于钳位型多电平逆变器的一大优点。共同充电的电容如果电压不能平衡会导致电压偏移，无法得到目标输出波形，甚至造成器件的损坏。本文所提逆变器的升压单元中电容1、2的所有状态完全一致，充分发挥了电容电压自平衡的优点。

由表1可知，在升压单元中，两个电容1、2的工作状态完全一致。逆变器的输出电压为0、和3时，电容1、2串联后共同充电；为0.5、1.5、2.5和3.5时，两电容并联后共同放电；为2和4时，两电容串联后共同放电。可以看出，电容1、2没有闲置状态。电容3单独充放电，不用考虑电容电压自平衡问题。输出电压为0、0.5、和1.5时，电容3处于闲置状态；为2时，3与升压单元并联充电；为2.5、3、3.5和4时，3与升压单元串联放电。

3.2 电容的额定电压与纹波计算

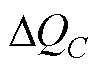
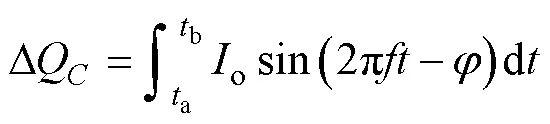
式中，o为逆变器负载侧的电流幅值；为负载电流的频率；为带感性负载时输出电压与负载电流的相位差。

Emission of Air Pollutants from Large Shipyards in Shanghai: Situation and Strategy……………XU Yong, LI Tie(2·10)

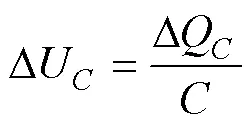
可以看出，影响电容电压纹波的因素有负载电流、连续放电时间和电容值。随着电容值的增加，电容的电压纹波不断减小。可以通过设计逆变器拓扑的充放电状态来控制连续放电时间，以及增加电容的容值来降低电容电压纹波。

为了控制电压纹波对逆变器拓扑造成的不良影响，一般限制电压纹波不能超过电容额定电压的10%。由于拓扑中电容的容值和额定电压均是可设计的，U为电容的额定电压，则可以得到容值和额定电压应满足的条件为

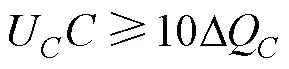
根据PWM原理，对正半周期的电容纹波进行分析。由调制比定义式可得载波幅值为

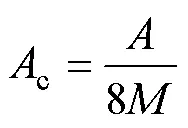
如图5a所示，逆变器输出电压的瞬时值从0到0.5对应的时间段为0～1，则

同理可得，=1, 2,…, 7时

=8, 9,…, 15时

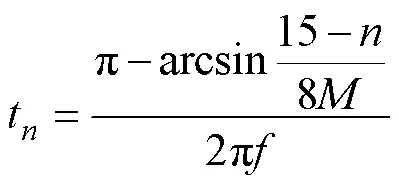
由表1和图5d可得，电容1、2的最长连续放电时间段为2～5和6～9，放电量分别为

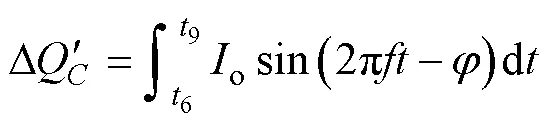
在一个工频周期内，电容1、2放电量一致，实现电容电压自平衡。电容3在时间段4～11内连续放电，放电量为

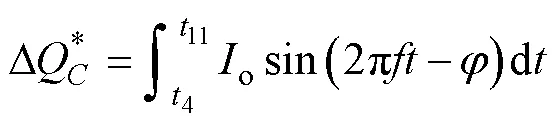
对比式（20）和式（18）、式（19）可知，在半个周期内，电容3的电荷变化量大于1、2，因此，电容3的电压纹波将大于1、2。

4 拓扑对比与分析

为了验证所提拓扑的优势，将其与已有的经典拓扑和最新的先进拓扑进行比较。为了使比较结果更明显与准确，所有拓扑均不使用级联拓展结构，而是使用只包含一个直流电源的拓展结构。表2给出了八种十七电平开关电容逆变器与所提出逆变器的参数对比，参数包括各逆变器使用的电容数、开关器件数（包括二极管）、开关的最大电压应力（Peak Inverse Voltage, PIV）、所有开关与二极管的总电压应力（Total Standing Voltage, TSV）。

表2 八种十七电平开关电容逆变器对比

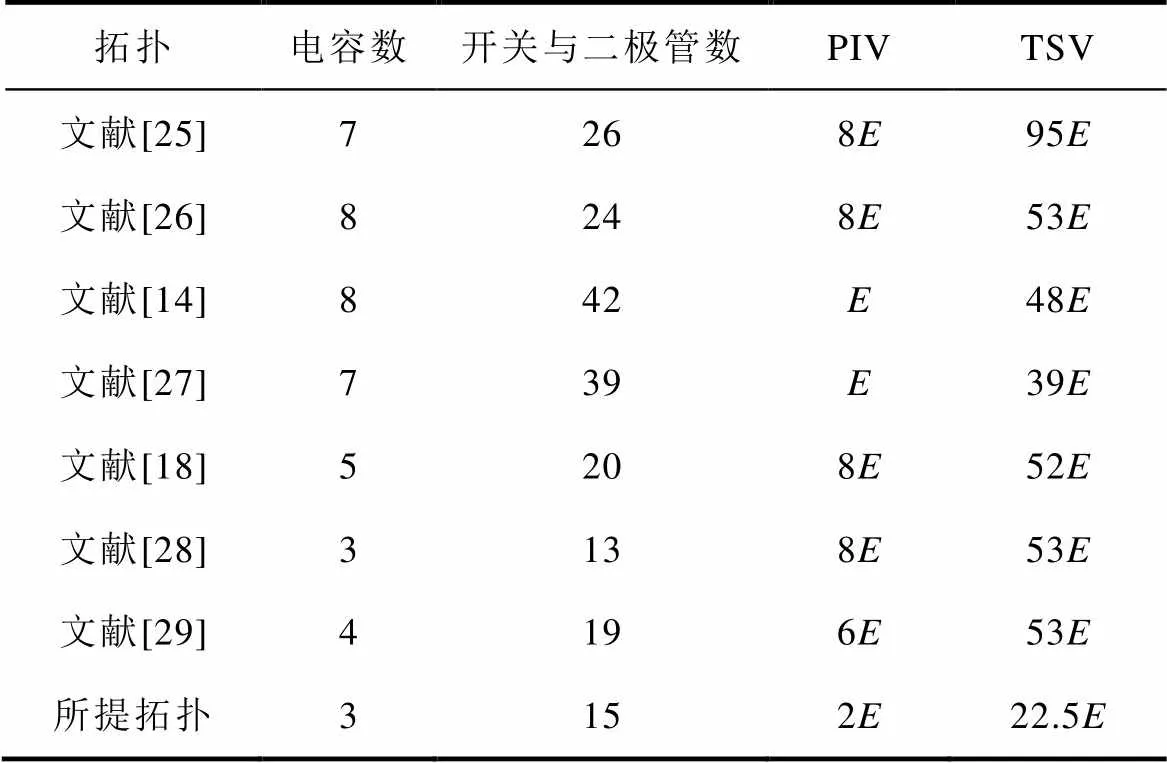
Tab.2 Comparison of several seventeen-level inverter

文献[25-26]提出的逆变器拓扑使用的是典型的H桥和开关电容组成的阶梯型升压单元。这类拓扑出现较早，优点是结构简单、易于拓展。虽然它使用的开关数较少，但总器件数较高；另一方面，使用H桥的拓扑其开关器件的电压应力都非常大。文献[14]中的拓扑使用了电容和开关组成的模块化结构。文献[27]中的拓扑则是将模块化结构和直流电源串联起来，以提高输出电压水平。这两种拓扑采用大量的电容和开关器件以实现最低的开关电压应力，其数值等于直流电源的电压。文献[18]中的拓扑使用直流电源与一个电容串联分别为另外两个电容充电，实现了升压能力，也降低了电容和开关数。但是它在开关电压应力和总电压应力上的表现依然不够理想。文献[28]所提拓扑使用前级电容与电源串联为后级电容充电，极大地降低了器件数量，但是电压应力依然很大。文献[29]中的拓扑则是通过一个双向开关将低压单元和高压单元连接起来，利用单个直流电源为两个开关电容单元同时充电以实现更高的输出电平，也能够较多地降低器件数量。该拓扑各项参数较为均衡。

从表2可以明显地看出，输出相同数量的电平时，所提拓扑使用的电容和开关器件数量远少于其他拓扑，所提拓扑的总电压应力远低于其他拓扑。至于电压应力，提出拓扑的最高电压应力仅高于文献[14, 27]所提拓扑。根据以上分析可得，本文提出的拓扑能够充分利用较少的器件，实现更多的输出电平并显著降低开关的电压应力。该拓扑特点鲜明、性能均衡，具有显著的经济性和广泛的适用性。

5 仿真与实验验证

5.1 仿真模型与结果分析

根据所提逆变器在实际工作中并网运行的需要，基于Matlab/Simulink平台搭建该逆变器及其控制系统的仿真模型，闭环控制系统结构如图6所示。该系统通过控制并网电流g跟踪指令值*以实现逆变器输出功率的变化。控制并网电流g的方式是保持其相位与电网电压g一致而幅值跟踪给定值m。系统通过锁相环（Phase-Locked Loop, PLL）获取电网电压g的相位，使其与给定的电流幅值m组成指令值*。将指令值*与并网电流g比较后得到的误差信号送入准比例谐振（Quasi Proportional Resonant, QPR）控制器，控制器的传递函数[30]为

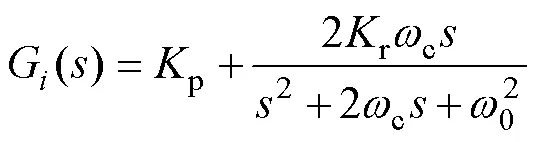
在仿真系统中，设计的滤波电感为5mH；带宽角频率c=0.2p，谐振角频率0=100p；比例增益系数p=50，谐振增益系数r=5 000。当并网电压有效值为110V，直流输入电压幅值为50V，输出频率为50Hz时，逆变器输出功率从250W变化到500W，并网电流跳变的仿真波形如图7a所示。当并网电压有效值为220V，输入电压幅值为100V时，逆变器输出功率从500W变化到1kW，仿真波形如图7b所示。从两组结果中可以看出，在时间=100ms时，并网电流迅速升高到目标值且无冲击电流。该仿真表明，并网电流能够迅速反应并稳定，证明了系统具有理想的稳态和动态性能。

图7 并网电压与逆变器输出电流波形

5.2 稳态实验与结果分析

为了验证所提逆变器功能的可行性，搭建了一台小功率实验样机对逆变器的稳态和动态性能进行实验。实验所用器件及其参数见表3。根据式（13）、式（16）～式（20）可以得到电容的计算值；考虑到留有一定的裕度，减小电容纹波，选择了2 200mF的电容设计值。

逆变器带阻性负载时，负载电流波形为阶梯波，与输出电压波形保持一致；逆变器带阻感性负载时，负载电流波形则为正弦波。图8给出了在直流输入电压为20V，阻感负载为100W、40mH的条件下，逆变器的交流输出电压与负载电流波形。图8中，输出电压的峰值为80V，逆变器实现了4倍电压增益；逆变器在稳定运行时能够输出标准的十七电平阶梯电压波形，其负载电流波形表现为平滑的正弦曲线。而且，负载电流波形滞后于输出电压波形，证明了该拓扑带感性负载的能力。

表3 实验参数

Tab.3 Experimental parameters

图8 逆变器输出电压与负载电流波形

稳态下逆变器电容电压波形如图9所示。电路稳定后，电容1、2的电压曲线基本一致，且电压纹波较小，证明了本文所提的逆变器拓扑具备电容电压自平衡的特性；电容3的电压波动范围较电容1、2更大，与理论分析一致；此外，电容1、2和3的电压能够稳定在设定的电压值附近。

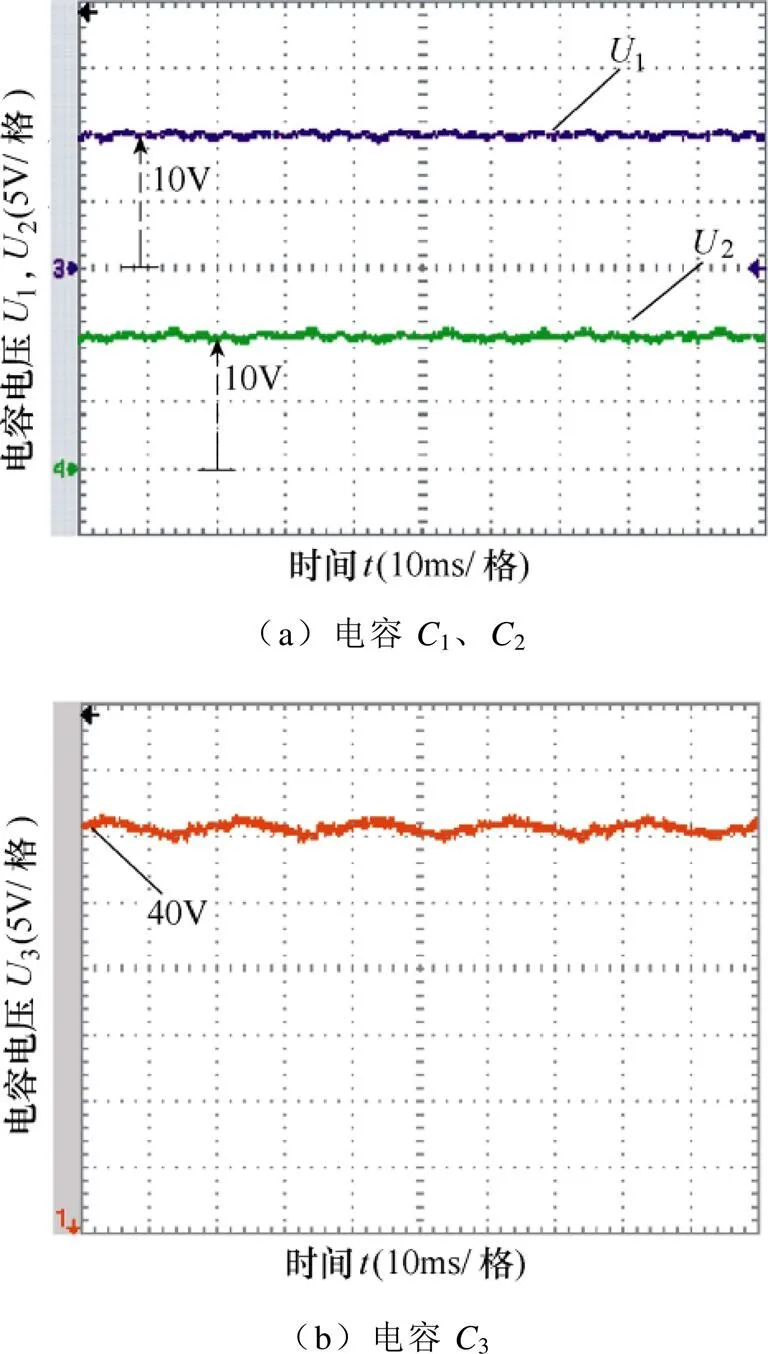
图9 稳态下电容电压波形

5.3 动态实验与结果分析

在输入电压为20V，载波频率为2 000Hz，输出频率为50Hz，负载电阻为100W的条件下，使用样机对逆变器调制比、输出频率、负载和输入电压四个方面的动态性能进行了实验验证。

图10为调制比改变时逆变器输出电压以及负载电流的波形。逆变器的调制比从0.9切换到0.5再切换到0.9时，逆变器输出电平数从十七电平变成九电平再变回十七电平。实验结果表明，在调制比变化时，本文所提逆变器能够迅速切换到目标状态并保持稳定。

图10 调制比变化实验的动态波形

图11给出了输出频率改变时逆变器的输出电压以及负载电流的波形。输出频率从50Hz变为100Hz再变为50Hz时，逆变器重新迅速稳定在新的工作状态。该实验表明，逆变器具备较大输出频率范围内的工作能力，响应迅速、稳定性好。

图11 输出频率变化实验的动态波形

图12为逆变器在负载变化时的输出电压以及负载电流波形。从图中可以看出：在负载从0变化到100W再变化到0时，逆变器输出电压保持不变；逆变器负载电流随着负载的变化先增大后减小。该实验表明，在负载变化时，逆变器的输出电压能够保持稳定，具有良好的适应负载突变的能力。

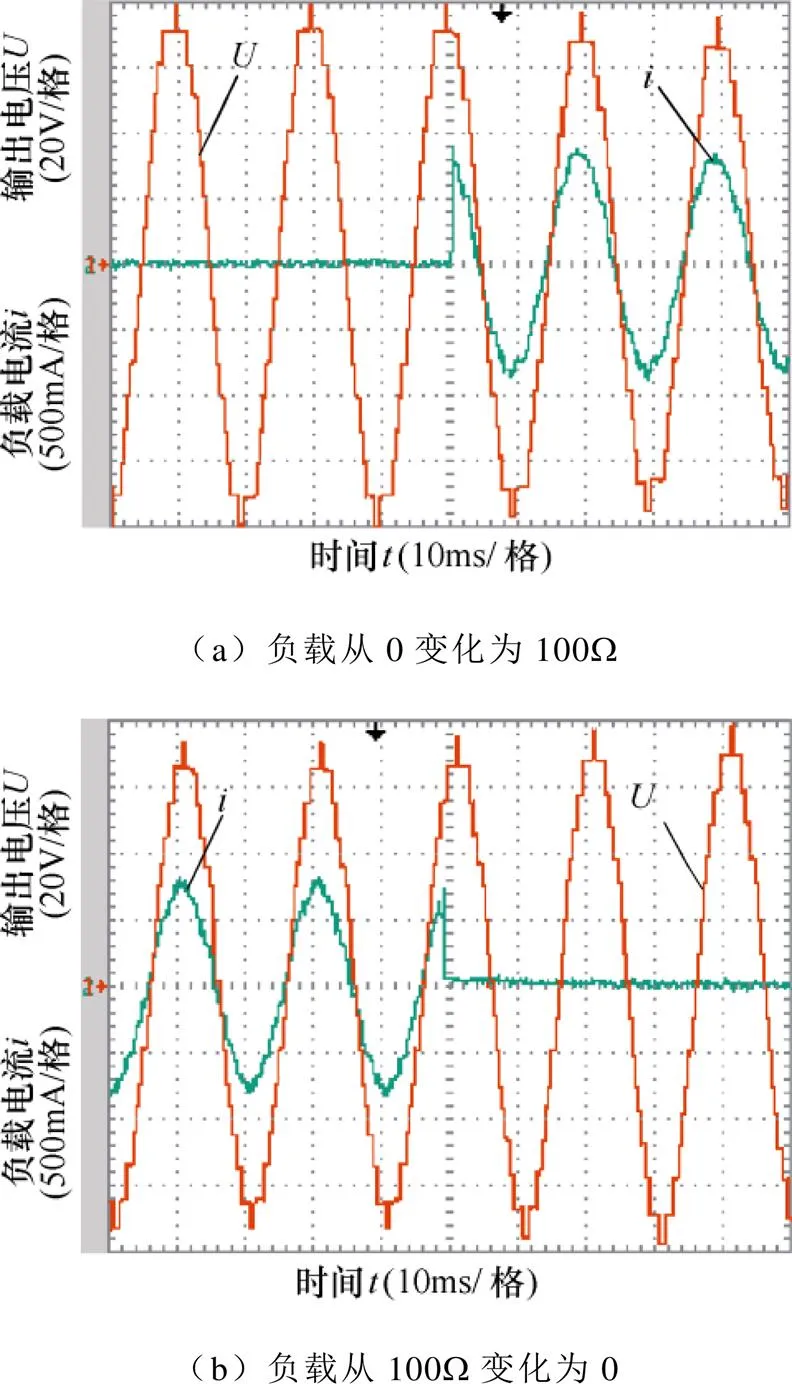
图12 负载变化实验的动态波形

图13给出了逆变器在直流输入电压从20V变化到15V再变化到20V时的输出电压和负载电流波形。从图中可以看出，直流输入电压从20V变化到15V再变化到20V时，逆变器输出电压相应地从80V变化到60V再变化到80V。在输入电压变化时，逆变器的输出能够迅速切换，且在变化时和稳定后保持了较高的电能质量。

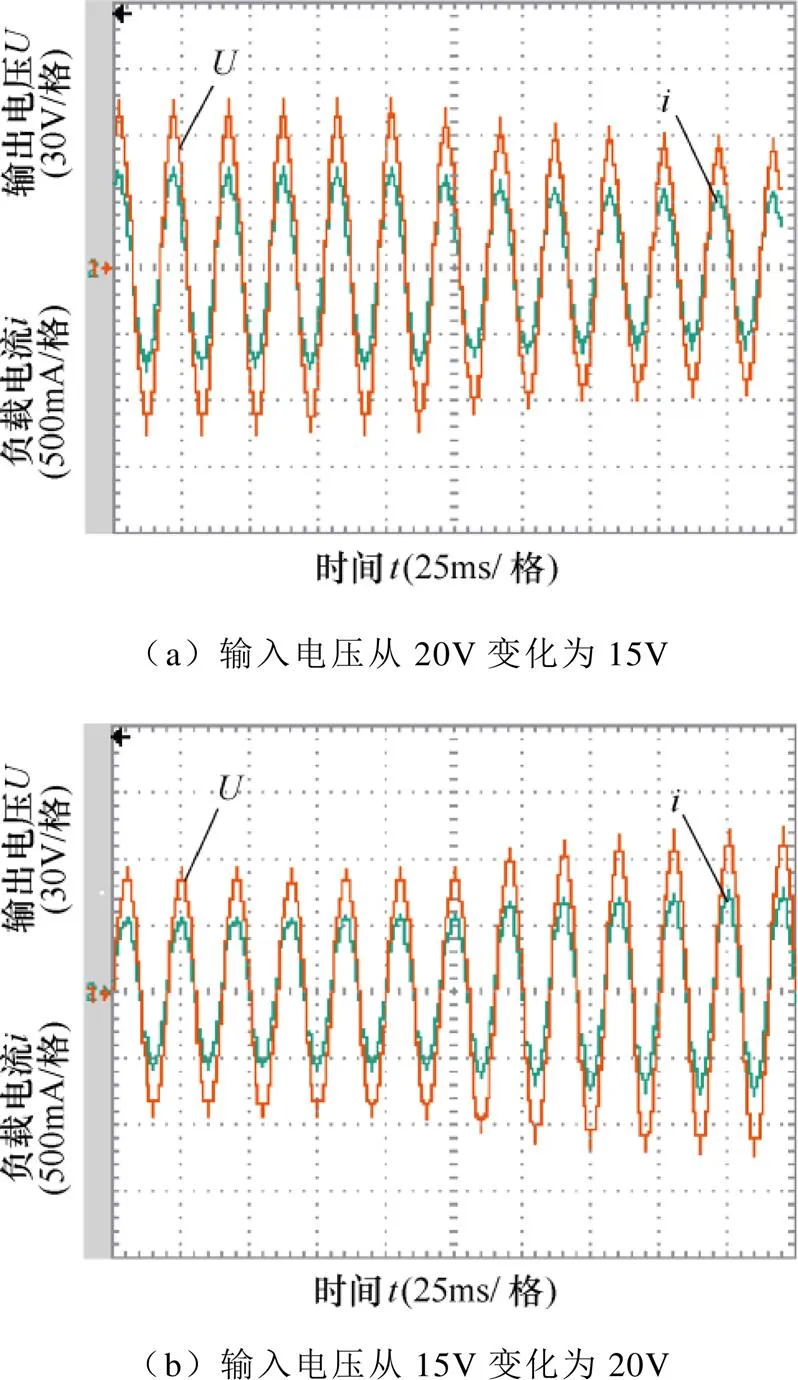
图13 输入电压变化实验的动态波形

从以上四个动态性能实验可知，逆变器对于输入电压变化、负载变化、输出频率变化和调制比变化响应迅速，在应对不同的工作状况时具有良好的动态性能。

6 结论

为了提高开关电容多电平逆变器的性能，本文提出了一种低应力高电平开关电容逆变器拓扑。从所提逆变器的拓扑结构、工作机理、调制策略、电容电压自平衡和电压纹波计算等多方面做了理论分析，并进行了样机实验，得出以下结论：

1）所提的逆变器拓扑能够使用1个直流电源、3个电容和15个开关输出十七电平的阶梯电压波形，具有开关电压应力低、电容纹波小的优点，且能够根据需要对拓扑进行拓展。

2）样机实验表明，所提拓扑具有电容电压自平衡、带感性负载的能力以及优良的动态稳定性。

3）与已有拓扑对比，本文所提拓扑在器件数、开关电压应力等方面具有明显的优势，在可再生能源发电领域中具有独特的性能优势和应用前景。

[1] 黄伟, 刘斯亮, 羿应棋, 等. 基于光伏并网点电压优化的配电网多时间尺度趋优控制[J]. 电力系统自动化, 2019, 43(3): 92-100.

Huang Wei, Liu Siliang, Yi Yingqi, et al. Multi- time-scale slack optimal control in distribution network based on voltage optimization for point of common coupling of PV[J]. Automation of Electric Power Systems, 2019, 43(3): 92-100.

[2] Zhang Xing, Wang Mingda, Zhao Tao, et al. Topolo- gical comparison and analysis of medium-voltage and high-power direct-linked PV inverter[J]. CES Transa- ctions on Electrical Machines and Systems, 2019, 3(4): 327-334.

[3] 钱强, 魏琦, 谢少军, 等. 单相并网逆变器多频阻抗模型及其在谐振环流分析中的应用[J]. 电力系统自动化, 2019, 43(15): 159-165.

Qian Qiang, Wei Qi, Xie Shaojun, et al. Multi- frequency impedance model of single-phase grid- connected inverter and its application in analysis of resonant circulating current[J]. Automation of Electric Power Systems, 2019, 43(15): 159-165.

[4] Ye Yuanmao, Chen Shikai, Zhang Xianyong, et al. Half-bridge modular switched-capacitor multilevel inverter with hybrid pulse width modulation[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 8237-8247.

[5] Mhiesan H, Wei Y, Siwakoti Y, et al. A fault-tolerant hybrid cascaded H-bridge multilevel inverter[J]. IEEE Transactions on Power Electronics, 2020, 35(12): 12702-12715.

[6] 王要强, 周成龙, 李忠文, 等. 单电源自均压九电平逆变器及其调制策略[J]. 电工技术学报, 2020, 35(4): 817-826.

Wang Yaoqiang, Zhou Chenglong, Li Zhongwen, et al. Single-source self-voltage-balancing nine-level inverter and its modulation strategy[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 817-826.

[7] 王鹏帅, 韩如成. 多电平逆变器主电路拓扑结构综述[J]. 自动化仪表, 2013, 34(10): 9-12,16.

Wang Pengshuai, Han Rucheng. Survey of the topological structure of main circuit of multilevel inverter[J]. Process Automation Instrumentation, 2013, 34(10): 9-12,16.

[8] 吴子阳, 肖岚, 姚志垒, 等. 基于滞环电流控制具有升压能力非隔离双接地光伏并网逆变器[J]. 中国电机工程学报, 2021, DOI: 10.13334/j.0258-8013.pcsee. 201699.

Wu Ziyang, Xiao Lan, Yao Zhilei, et al. Double- grounded transformer-less photovoltaic grid-connected inverter with boost capacity based on hysteresis current control[J]. Proceeding of the CSEE, 2021, DOI: 10.13334/j.0258-8013.pcsee.201699.

[9] Fang Xupeng, Tian Yingying, Ding Xiaokang, et al. Series-type switched-inductor Z-source inverter[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(1): 53-60.

[10] Peng Wei, Ni Qiang, Qiu Xiaohua, et al. Seven-level inverter with self-balanced switched-capacitor and its cascaded extension[J]. IEEE Transactions on Power Electronics, 2019, 34(12): 11889-11896.

[11] Vijeh M, Rezanejad M, Samadaei E, et al. A general review of multilevel inverters based on main sub- modules: structural point of view[J]. IEEE Transa- ctions on Power Electronics, 2019, 34(10): 9479- 9502.

[12] 王要强, 袁艺森, 陈天锦, 等. T型开关电容可扩展多电平逆变器[J]. 电工技术学报, 2020, 35(24): 5115-5124.

Wang Yaoqiang, Yuan Yisen, Chen Tianjin, et al. Extensible T-type switched capacitor multilevel inverter[J]. Transactions of China Electrotechnical Society, 2020, 35(24): 5115-5124.

[13] 曾君, 吴佳磊, 刘俊峰, 等. 一对基于开关电容原理的多电平高频逆变器[J]. 电工技术学报, 2018, 33(6): 1312-1319.

Zeng Jun, Wu Jialei, Liu Junfeng, et al. A pair of high-frequency multilevel inverters based on switched-capacitor technique[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1312-1319.

[14] Jahan H K, Abapour M, Zare K. Switched-capacitor based single-source cascaded H-bridge multilevel inverter featuring boosting ability[J]. IEEE Transa- ctions on Power Electronics, 2019, 34(2): 1113-1124.

[15] Samizadeh M, Yang X, Karami B, et al. A new topology of switched-capacitor multilevel inverter with eliminating leakage current[J]. IEEE Access, 2020, 8: 76951-76965.

[16] Siddique M D, Mekhilef S, Sanjeevikumar P, et al. Single phase step-up switched-capacitor based multi- level inverter topology with SHEPWM[J]. IEEE Transactions on Industry Applications, 2020, DOI: 10.1109/TIA.2020.3002182.

[17] Siddique M D, Mekhilef S, Shah N, et al. A single DC source nine-level switched-capacitor Boost inverter topology with reduced switch count[J]. IEEE Access, 2020, 8: 5840-5851.

[18] Nakagawa Y, Koizumi H. A Boost type nine-level switched capacitor inverter[J]. IEEE Transactions on Power Electronics, 2019, 34(7): 6522-6532.

[19] Liu Junfeng, Lin Weijie, Wu Jialei, et al. A novel nine-level quadruple Boost inverter with inductive-load ability[J]. IEEE Transactions on Power Electronics, 2019, 34(5): 4014-4018.

[20] Amir T, Adabi J, Mohammad R. A multilevel inverter structure based on a combination of switched- capacitors and DC sources[J]. IEEE Transactions on Industrial Informatics, 2017, 13(5): 2162-2171.

[21] Samadaei E, Kaviani M, Bertilsson K. A 13-levels module (K-type) with two DC sources for multilevel inverters[J]. IEEE Transactions on Industrial Elec- tronics, 2018, 66(7): 5186-5196.

[22] 张琦, 李江江, 孙向东, 等. 单相级联七电平逆变器拓扑结构及其控制方法[J]. 电工技术学报, 2019, 34(18): 3843-3853.

Zhang Qi, Li Jiangjiang, Sun Xiangdong, et al. Topology and control method of single-phase cascaded seven-level inverter[J]. Transactions of China Elec- trotechnical Society, 2019, 34(18): 3843-3853.

[23] 高瞻, 李耀华, 葛琼璇, 等. 低载波比下三电平中点钳位变流器改进型同步载波脉宽调制策略研究[J]. 电工技术学报, 2020, 35(18): 3894-3907.

Gao Zhan, Li Yaohua, Ge Qiongxuan, et al. Research on improved synchronized carrier based PWM for three-level neutral point clamped converter under low carrier ratio[J]. Transactions of China Electro- technical Society, 2020, 35(18): 3894-3907.

[24] Darus R, Pou J, Konstantinou G, et al. A modified voltage balancing algorithm for the modular multi- level converter: evaluation for staircase and phase- disposition PWM[J]. IEEE Transactions on Power Electronics, 2015, 30(8): 4119-4127.

[25] Ye Yuanmao, Cheng K W E, Liu Junfeng, et al. A step-up switched-capacitor multilevel inverter with self-voltage balancing[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12): 6672-6680.

[26] Youhei H, Hirotaka K. A switched-capacitor inverter using series/parallel conversion with inductive load[J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 878-887.

[27] Taghvaie A, Adabi J, Rezanejad M. A self-balanced step-up multilevel inverter based on switched- capacitor structure[J]. IEEE Transactions on Power Electronics, 2018, 33(1): 199-209.

[28] Zamiri E, Vosoughi N, Hosseini S H, et al. A new cascaded switched-capacitor multilevel inverter based on improved series-parallel conversion with less number of components[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3582-3594.

[29] 叶远茂, 林明亮. 基于开关电容的单电源升压型多电平逆变器[J]. 中国电机工程学报, 2020, 40(17): 5636-5643.

Ye Yuanmao, Lin Mingliang. Single source step-up multilevel inverter based on switched-capacitor[J]. Proceedings of the CSEE, 2020, 40(17): 5636-5643.

[30] 杨庆文, 何绍民, 杨欢, 等. 考虑故障特性模拟的虚拟电机系统及其控制[J]. 电工技术学报, 2020, 35(6): 1239-1250.

Yang Qingwen, He Shaomin, Yang Huan, et al. Virtual motor system considering fault characteristic simulation and its control strategy[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1239- 1250.

Topology and Modulation Strategy for Switched Capacitor Inverter with Low Voltage Stress and High Level

1,21,21,21,21,3

（1. School of Electrical Engineering Zhengzhou University Zhengzhou 450001 China 2. Henan Engineering Research Center of Power Electronics and Energy Systems Zhengzhou 450001 China 3. Cardiff University Cardiff CF243AA U.K.）

In order to improve the boost capability and output power quality of inverters in the renewable energy power generation system, this paper proposed a switched capacitor inverter with low voltage stress and high-level characteristics. The proposed topology has one input DC source, three capacitors and fifteen switching devices, which can achieve four times voltage gain and seventeen-level output waveform. Compared with other topologies, the performance of the proposed inverter can generate more output levels with fewer switching devices, reducing the voltage stress of switching devices and the harmonic content of inverter output voltage. Moreover, the inversion process can be realized without a back-end H-bridge, and the voltage stress of switches is reduced effectively. In addition, the proposed inverter has small voltage ripple, and the capacitor voltage self-balancing performance simplifies the complexity of the controller. The paper introduces the topology, working principle, and modulation strategy of the proposed inverter in detail, and analyzes the calculation of voltage ripples. The proposed inverter shows excellent performance compared to various switched capacitor topologies. Finally, the feasibility of the proposed inverter and the correctness of the theoretical analysis are verified by the experimental results.

Multilevel inverter, switched capacitor, low voltage stress, high output level, capacitors voltage self-balancing

10.19595/j.cnki.1000-6753.tces.210241

TM464

王要强 男，1982年生，博士，副教授，主要研究方向为电力电子变换、可再生能源发电、柔性交直流输配电、电机驱动控制等。E-mail: WangyqEE@163.com

赖锦木 男，1990年生，博士，讲师，主要研究方向为电力电子变换与控制技术及其在交直流灵活配电等方面的应用。E-mail: laijinmu@126.com（通信作者）

2020-03-01

2020-04-25

国家自然科学基金项目（51507155）和河南省高等学校青年骨干教师项目（2019GGJS011）资助。

（编辑 陈 诚）