频率域薄储集层预测技术在煤系地层中的应用

冯昕鹏，王涛，白志涛，聂万才，何争光

（1.东方地球物理公司 研究院 长庆分院，西安 710021；2.中国石油 长庆油田分公司a.宜黄天然气项目部，西安 710018；b.第一采气厂，西安 710000）

鄂尔多斯盆地东部气田包含北部神木、中部米脂和南部宜川3 大气田，位于伊陕斜坡东部[1]，是油田增储上产的主力区。该区构造平缓，平均坡降6～10 m/km；下二叠统太原组和中二叠统山西组山2 段为主力产层，分别属于海陆过渡相和三角洲前缘相沉积，均是受优质砂岩储集层控藏的致密岩性气藏[2-3]。前期，多口井在太原组和山2段钻遇10×104m3/d以上的高产气藏，随着勘探深入，以“小而肥”为特征的砂岩气藏更加难以识别，储集层预测准确率较低。地震和地质结合分析认为，储集层预测失利的原因主要有2点：①山2段和太原组储集层薄，平均厚度分别为13.3 m 和9.2 m，砂体横向变化快，地震数据主频低，为25～30 Hz，时间域分辨率为20～25 m，远大于储集层厚度；②山2 段中下部4+5 号煤层和太原组底部9 号煤层全盆地发育，煤层形成的强反射屏蔽了砂泥岩弱反射，薄储集层识别难度大。

前人利用波形特征分析、地震属性、反演等方法在煤系地层中进行薄储集层预测，取得了一定的成效。如利用广义S变换剖面对煤层厚度较小的4+5号煤层所在的山2 段的薄砂体进行了预测，并取得了较好的效果，但没有对煤层厚度较大的9 号煤层所在的太原组的薄砂体进行预测[4]；利用多子波分解与重构技术去除反映煤层子波后的重构数据定性预测储集层含气性，缺少对储集层的精细刻画[5]；利用时频分析方法定位煤层频带，将目的层段地震数据中的该频带删除，从而消除煤层影响以刻画薄储集层，但直接删除对煤层敏感的低频带，可能造成有效信号的删除[6]；通过分析测井曲线对岩性变化敏感性，采用密度和中子曲线构建拟声波曲线以削弱煤层影响，再通过反演刻画薄储集层，该方法受到井控程度的限制[7]。针对研究区目的层段煤层多、储集层薄且预测难的现状，本文重点阐述利用地震频率信息预测薄层的原理，并优选了从时间域到频率域的时频转换方法；为进一步提高对薄层的识别能力，首先采用成熟的多子波分解与重构技术压制煤层强反射，在此基础上再用地震频率域数据预测薄层，识别效果较好。

1 地震频率域薄层预测理论基础

由于地震波在薄层中的调谐作用，在时间域难以识别小于1/4波长厚度的薄层。将时间域地震数据转换到频率域进行时频域联合分析，可以突破1/4 波长分辨率极限[8]。傅里叶变换是信号时频分析的经典方法，能实现信号在时间域或频率域的无损转换，但傅里叶变换是时间域上全局变换，无法表述信号在时频域的局部性质，即不知道频率域中某一频率分量是什么时候产生的。为了分析和处理非平稳信号的局部特征，在傅里叶变换的基础上增加时窗[9-11]：

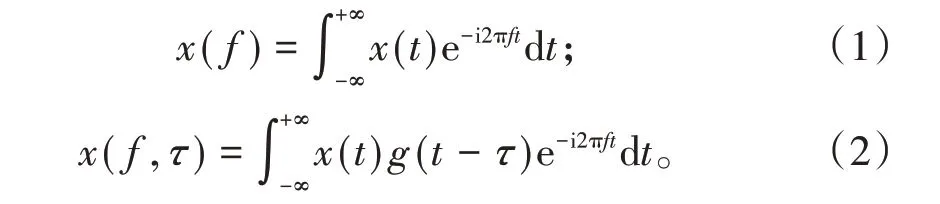
（2）式在（1）式傅里叶变换的基础上增加了窗函数g(t-τ)，相当于在[τ-δ,τ+δ]和[f-ε,f+ε]区域内的状态，此区域称为时窗，δ和ε分别为时窗的时宽和频宽，时窗宽越小，分辨率越高。窗函数使x(t)在不同有限时间宽度内近似为平稳信号，能够分析不同时刻的信号，从而凸显了突变信号的局部特征。时窗宽很小，即δ和ε都非常小，才能在时频域有很高的分辨率，但根据海森堡测不准原理，δ与ε相互制约，两者不可能同时都任意小，且满足δε≥1/(4π)，取等号时，窗函数为高斯函数。

1.1 短时傅里叶变换

Dennis Gabor 于1946 年引入了短时傅里叶变换，基本思想是用窗函数来截取信号，假定信号在时窗内是平稳的，采用傅里叶变换分析时窗内的信号，以确定时窗内存在的频率成分，然后沿着信号时间方向移动窗函数，得到频率随时间的变化关系，即所需的时频分布[10]。如（2）式所示，由于短时傅里叶变换的时窗大小固定，即时频网格等宽（图1a），不能随频率需要，使时窗变宽或变窄，不利于检测高频信号。

图1 短时傅里叶变换和小波变换Fig.1.Short⁃window Fourier transform and wavelet transform

1.2 小波变换

小波变换由Morlet在1974年提出，具有较快的衰减性，振幅只能在一个很短的区间上非零，常用的基本小波有Morlet小波、Paul小波和MexicanHat小波。

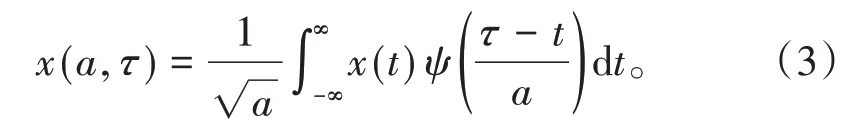
时窗随着信号频率的变化而变化，即在信号低频部分采用宽时窗，在高频部分采用窄时窗（图1b），从而提高了信号处理的分辨率。调节窗函数，即基本小波ψ(t)的平移因子和伸缩因子，可实现小波变换的多分辨率分析[12-15]。

1.3 S变换和广义S变换

若窗函数为（4）式的高斯函数，则（2）式演变为（5）式，即S变换：

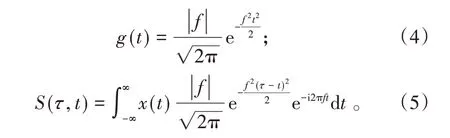
由于S 变换中的基本小波固定，不能随具体的应用而调整，缺乏灵活性，使得时间和频率分辨率受到一定限制，对此，前人对窗函数提出了改造：

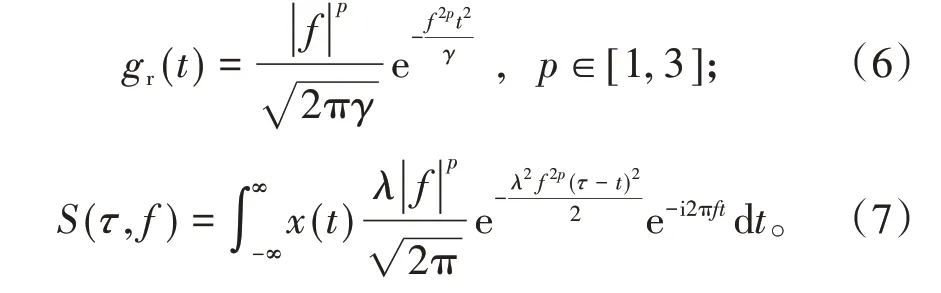
（6）式为改造后的窗函数，（7）式即广义S 变换，该变换通过引入线性调节因子和指数调节因子，改造了S 变换，使其能根据实际应用中非平稳信号的频率分布特点和时频分析的侧重点，灵活地调节小波随频率的变化趋势，可以进一步加快或减慢小波的时宽随信号频率变化的速度，即指数调节因子一定时，线性调节因子大于1，加快了高斯时窗宽度随信号频率呈反比的速度；反之，线性调节因子小于1，此种速度减慢。同时小波的振幅呈现多种变化特征，从而使广义S 变换能够更好地适应具体信号的分析和处理。当线性调节因子和指数调节因子均为1时，即S变换。

地震信号属于非平稳信号，即频率不随时间变化呈规律性的变化，因此需借助变时窗的时频分析方法来进行分析，广义S 变换和小波变换克服了短时傅里叶变换时窗固定的缺点，能根据信号频率变化自适应调节时窗。相对小波变换，广义S 变换引入新的相空间测度，具有更高的分辨率和稳定性，且与傅里叶谱有直接联系，物理意义更明确[16-17]。

广义S 变换能根据地震数据处理的具体要求灵活地调节小波函数的参数，不会对储集层的时频响应特征产生影响，保证了在地震数据处理中的良好适应性，可以用于分辨较薄的储集层[18]。

1.4 模型正演分析

根据研究区太原组和山2 段岩性组合关系及地层厚度建立含煤砂泥岩地质模型（图2a），各岩性地球物理参数如表1 所示，为了对比分析上述各时频分析方法对薄层的分辨率，先不考虑煤层影响，即简化为图2b 所示纯砂泥岩地质模型。选取与研究区地震数据主频一致的30 Hz雷克子波与砂泥岩地质模型反射系数褶积，生成如图3a 所示正演剖面，并计算砂泥岩界面地震反射波形最大波峰振幅。从图3b 中可见，随着砂体厚度增大，振幅增强，当砂体厚度为1/4波长时，振幅达到最强，随着厚度继续增大，振幅强度则减弱至趋于稳定。因此，在时间域利用振幅强度和时间均不能反映砂体厚度。

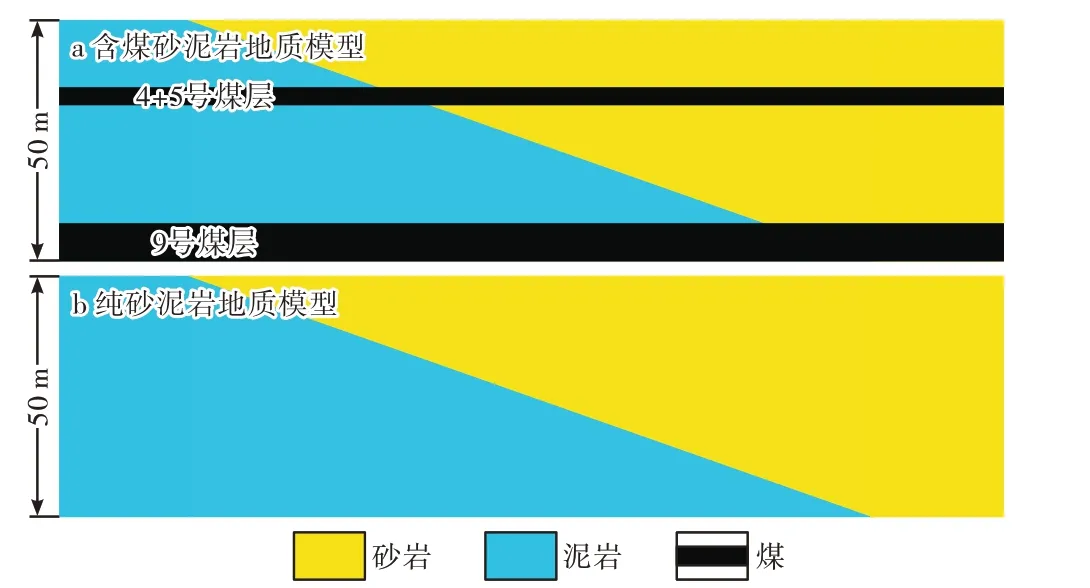
图2 研究区含煤砂泥岩和纯砂泥岩地质模型Fig.2.Geological models of coal⁃bearing and pure sandstone and shale in the study area

表1 研究区目的层段地球物理参数Table 1.Geophysical parameters of target intervals in the study area

分别运用短时傅里叶变换、小波变换（Mexican⁃Hat 小波）、小波变换（Morlet 小波）及广义S 变换对正演波形进行时频转换。首先对每种变换结果进行频率变化的敏感性分析，对比发现，短时傅里叶变换对频率敏感性最差，其次是小波变换（MexicanHat 小波），广义S 变换对频率敏感性最强。根据地震频带（8～60 Hz）选取最高频率60 Hz 时频剖面（图4），分析其分辨率，从图4 中可见小波变换（MexicanHat 小波）分辨率最高，但当砂体厚度为30～40 m 时，砂体底界几乎无反射，导致砂体厚度刻画不准，且当砂体厚度

效压制了煤层强反射后，设置时窗、时间分辨率和频率分辨率，时频转换得到频率域剖面（图7）。Well2井山2 段和太原组砂体厚度分别为15.2 m 和7.8 m，Well3 井山2 段和太原组砂体厚度分别为13.8 m 和12.4 m。叠前时间偏移剖面上2个煤层反射之间基本没有储集层反射；广义S 变换剖面与煤层强反射压制后广义S 变换剖面对比发现，广义S 变换剖面上山2段砂体没有刻画出来，煤层强反射压制后，再进行广义S 变换，刻画的砂体厚度与实钻井完全吻合；煤层强反射压制后，短时傅里叶变换剖面分辨率低，小波变换（MexicanHat 小波）剖面虽具有高分辨率，但有明显的假频现象，不是对砂体厚度的真实反映。综上所述，广义S 变换剖面弥补了短时傅里叶变换、小波变换（MexicanHat 小波）的缺点，更为准确地刻画了砂体厚度，砂体横向变化也得到了很好的反映。

图6 研究区多子波分解与重构技术压制煤层强反射前、后剖面对比Fig.6.Sections before and after suppressing strong reflections from coal seams by multi⁃wavelet decomposition and reconstruction

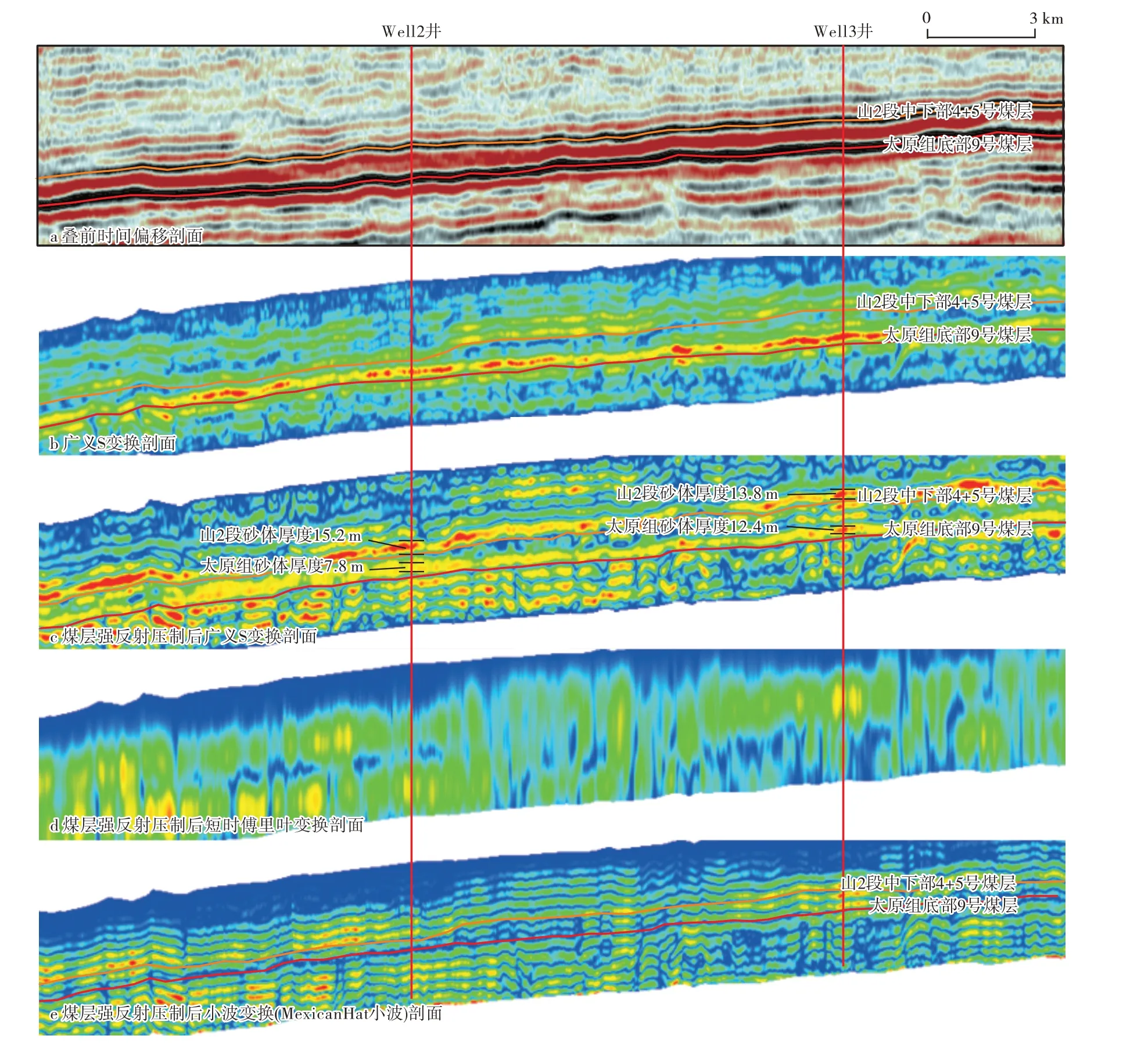
图7 研究区应用时频剖面预测储集层效果对比Fig.7.Results from using time⁃frequency section to predict reservoirs in the study area

利用测网密度为1.3 km×1.6 km 的地震数据对米脂气田余兴庄地区太原组薄砂体进行预测。压制煤层强反射后，进行广义S 变换，预测太原组砂体厚度，并内插得到砂体厚度分布（图8），与地质解释太原组砂体厚度分布（图8a）对比，广义S 变换预测太原组砂体厚度分布（图8b）更加细化，清晰展示了2条主砂体来源于北部物源方向，受东南部海水冲刷，东南部砂体欠发育；余兴庄地区共9 口井钻遇太原组砂体，其中7 口井预测的太原组砂体厚度与实钻井吻合，符合率为77.8%，预测可靠性高，为下一步井位部署提供了依据。

图8 米脂气田余兴庄地区太原组砂体厚度分布Fig.8.Thickness distributions of sandstone reservoirs of the Taiyuan formation in the Yuxingzhuang area in Mizhi gas field

3 结论

（1）根据鄂尔多斯盆地东部气田太原组和山2 段地层结构，建立砂体厚度变化的地质模型，通过模型正演、时频分析方法对比，广义S 变换生成的频率体数据对厚度变化的敏感性最好，薄层分辨率最高。

（2）为提高薄层厚度预测的准确率，首先采用多子波分解与重构技术压制煤层强反射，突出砂岩弱反射后，将地震数据转换至频率域，提高薄层识别能力。通过在鄂尔多斯盆地东部米脂气田薄储集层预测中的应用，储集层分辨率提高至5 m，预测符合率提高到77.8%，应用效果较好，为明确鄂尔多斯盆地煤系地层中薄储集层的展布规律奠定了基础。

符号注释

a——伸缩因子；

f——频率，Hz；

g(t)——窗函数；

g(t-τ)——在τ时刻的窗函数；

gr(t)——改造后的窗函数；

i——虚数单位；

p——广义S变换中的指数调节因子；

S(τ,f)——广义S变换；

S(τ,t)——S变换；

t——时间变量，s；

x(a,τ)——将基本小波ψ(t)伸缩a倍后的时频变换；

x(f)——时间函数x(t)的时频变换；

x(f,τ)——时间函数x(t)在τ时刻的时频变换；

x(t)——时间函数；

γ——能量衰减率；

τ——时间，s；

λ——广义S变换中的线性调节因子；