大斜度井及水平井垂向纵波时差在页岩孔隙度评价中的应用

郑健，傅永强，陈满，井翠，张婧，周昊，张家浩

（1.四川长宁天然气开发有限责任公司，成都 610000；2.中国石油测井有限公司 辽河分公司，辽宁 盘锦 124010）

随着北美页岩油气开发研究的不断深入，中国页岩气资源也逐渐得到重视，先后在四川、云南、重庆等区域建立了页岩气开发示范区，通过构造演化确定页岩形成的有利环境，利用地质分析、测井评价、地震追踪等方法研究页岩的空间分布特征和储集性能，获得页岩气有利区带[1-2]。用测井评价页岩储集层的地球化学特性、储集性能、含气性、脆性矿物指数等，为准确评价页岩气田提供依据[3]，地球化学特性、储集性能和含气性是页岩气的资源评价项目，脆性矿物指数是储集层压裂改造的重要依据[4-5]，据此优选页岩气甜点区，实现海相页岩气资源的有效开发，埋深3 500 m以浅的海相页岩气区已经建成年产200×108m3的规模[6]。测井评价页岩储集层参数主要是通过岩心标定测井理论模型或岩心与测井资料建立区域参数模型计算获取，声波测井系列资料是评价页岩储集层物性、岩石力学等的基础资料，无论是孔隙度模型，还是岩石力学参数模型，纵波时差都是关键资料[7-8]。在四川盆地长宁页岩气开发示范区，大斜度井及水平井应用纵波时差计算孔隙度时，采用岩心标定的平均时间响应公式或在岩心资料基础上建立的含纵波时差的多元孔隙度模型中，通过纵波时差计算的孔隙度与实际孔隙度存在较大差异，严重影响页岩储集层评价的准确性，其主要原因是页岩具有弹性各向异性，因此，必须对纵波时差资料进行各向异性校正后，才能获得页岩储集层评价的准确结果。

1 纵波各向异性

随着对声波和地层的深入研究，对声波在各向异性地层中的传播特性的认识也逐渐加深，认识到地层弹性各向异性对声波在岩层中的传播有一定影响。Backus 等在1962 年认识到水平各向同性多层介质组合引起弹性参数的各向异性[9]；Berryman 等在1979 年对横向各向同性地层的声波弹性各向异性进行研究，建立了利用相速度表示群速度的关系式，得出在相角等于0°或90°时，群速度等于相速度[10]。Thomsen 在1986 年进一步研究认为，地球物理研究的各类地层均为弱各向异性介质，提出了5个弹性参数α0、β0、ε、γ和σ替代定义各向异性的5个弹性参数c11、c33、c44、c66 和c13，其中α0和β0分别是纵波速度和横波速度，ε和γ分别代表纵波与横波在垂直和水平方向的速度差异，σ取决于各向异性，又与ε 相关，如果σ和ε 相等，纵波的速度面为椭圆形，垂直极化横波波速面是球体，称为椭圆各向异性，绝大多数页岩的ε 大于σ，这种情况表现为正椭圆各向异性，正椭圆各向异性固体特征与椭圆各向异性对比，声波在有一定斜角的地层中传播时，纵波传播速度更快，而垂直极化横波更慢[11]，该研究使通过测量不同角度传播的纵波波速或纵波时差直接描述各向异性成为可能。Vernik 等于1997 年在不同有效应力条件下，对不同干酪根含量、黏土矿物组分和孔隙度的页岩进行声波速度各向异性测量，从岩心实验发现页岩具有较强的各向异性，对声波速度的影响不容忽视，且随压实程度的增加而增加[12]；但在工程中纵波是近垂直测量，难以通过比较水平速度和垂直速度评价各向异性。随着页岩油气开发，大斜度井及水平井被广泛应用，利用测井直接评价各向异性成为可能。Miller 等在2012 年对北美页岩气直井和水平井偶极声波测井进行研究，采用三维差分建模，模拟声波在不同井斜角下群速度与相速度变化，通过理论模拟和实例均证明了声波测井测量波列提取的时差为群速度时差，群角等于井斜角，而不是假设以相速度传播的相角等于井斜角[13]。Horne等对北美海恩斯维尔页岩储集层的声波测井进行研究发现，这类各向异性页岩气层产生的有效各向异性具有垂直对称性，分析海恩斯维尔页岩弹性各向异性对声波在大斜度井及水平井的影响，提出了对偶极声波测井各测量的传播速度进行计算的方法[14]。刘鹤等在2017 年在垂向异性地层中模拟高速层、岩屑床、井斜角、各向异性等对大斜度井及水平井声波时差的影响，模拟声波在各向异性地层中传播，在近井筒存在高速层声学理论不适用，而岩屑床影响可以忽略不计，各向同性地层中声波速度不受井斜角影响，模拟不同井斜角和各向异性获得纵波时差，建立不同井斜角和各向异性条件下测量纵波时差与垂向纵波时差误差图版[15]。

地层各向异性越来越受到重视，其对声波测井有较大的影响，尤其对页岩这类垂直横向各向同性地层的影响更为显著，测井的纵波时差与井斜角、地层纵波各向异性参数ε 相关，各向异性参数越大，井斜角越大，直井与大斜度井及水平井纵波时差差异越大，井斜角达到90°时，差异达到最大；同时也为利用测量的纵波时差计算垂向和水平纵波时差提供了理论依据。无论是计算储集层参数模型，还是计算岩石力学参数模型，均需要岩心标定或刻度参数模型[16]。四川盆地长宁页岩气开发示范区取心井通常为低井斜角（直井或井斜角小于3°）的井，利用岩心分析资料和测井资料建立刻度及标定系数，其标定系数仅适用于直井。因此，在大斜度井及水平井中采用直井标定的孔隙度模型计算孔隙度存在较大误差，需要消除各向异性及井斜角对大斜度井及水平井声波时差的影响。本文利用直井与大斜度井及水平井纵波时差变化关系，直接计算大斜度井及水平井的垂向纵波时差，利用直井建立的孔隙度模型获得大斜度井及水平井储集层孔隙度。

2 大斜度井及水平井声波时差计算方法

四川盆地长宁页岩气开发示范区采用直井对页岩气藏进行综合评价，采用大斜度井及水平井进行开发，为建立大斜度井及水平井横向纵波时差与垂向纵波时差的差异提供了基础。直井与水平井水平位移不超过1 500 m（图1a），选取相同且井斜较稳定的层段，分段统计测量的纵波时差和井斜角，可以获得纵波时差与井斜角的关系（图1b）；也可采用极坐标表示测量纵波时差与水平纵波时差、垂向纵波时差、井斜角的关系，得出拟合后纵波时差与井斜角的关系（图1c）。页岩地层因水动力条件极弱，横向变化较小，直井与水平井在目的层横向距离较小，因此假设在研究范围内同层段页岩的测井响应变化较小，水平井测量的纵波时差的变化完全归因于各向异性影响，则可利用对应同层段平均纵波时差建立纵波时差与井斜角的函数关系来消除井斜角的影响。

图1 研究区纵波时差与井斜角的关系Fig.1.Relationships between P⁃wave slowness and well deviation in the study area

2.1 直接拟合法

纵波时差与井斜角的拟合关系式可以表示为f(θ)，当井斜角θ为0°时，由拟合关系式可得地层垂向纵波时差Δtv；当井斜角θ为90°时，可得地层水平纵波时差Δth。当井斜角为θ时，各向异性导致的垂向纵波时差和校正量：

式中f(θ)——纵波时差与井斜角的拟合关系式；

θ——井斜角，（°）；

Δt——测量纵波时差，μs/m；

Δtv——垂向纵波时差，μs/m；

Δtθ——井斜角为θ时的垂向纵波时差校正量，μs/m。

同理，可以获得水平纵波时差和校正量。

从直接拟合法可以得出，在计算纵波时差校正量时只与水平井井斜角相关，目的层纵波时差变化较小时可以获得较好的效果。垂向上矿物含量、总有机碳含量、孔隙度、岩石物理特性等的差异，均会导致垂向纵波时差变化，对于垂向变化较大的地层，通过各向异性椭圆模型法计算垂向纵波时差效果更好。

2.2 各向异性椭圆模型法

Thomsen 定义各向异性的弹性参数ε=Δtv/Δth，且纵波在各向异性地层中的传播速度与地层角度呈椭圆分布。ε在目的层变化小时，可以假设为常数，根据纵波椭圆各向异性（图1c），在极坐标系下，水平纵波时差、垂向纵波时差、井斜角下测量的纵波时差物理意义十分清晰，极坐标点（Δt，θ）分别为测量纵波时差和井斜角，极角0°时，极半径为垂向纵波时差，极角为90°时，极半径为水平纵波时差。井斜角为θ时，测量纵波时差：

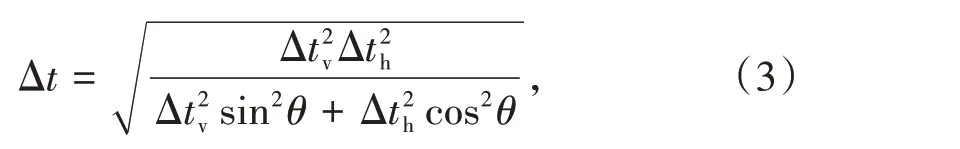
式中 Δth——水平纵波时差，μs/m。

通过（3）式可得到ε，利用ε、θ、Δt和（3）式可得垂向纵波时差：

利用Δtv、ε和Δth，可以评价页岩储集层物性和岩石力学性质。

3 应用实例

3.1 长宁页岩气开发示范区构造及储集层特征

长宁页岩气开发示范区位于川南古坳中隆低陡变形带和娄山褶皱带，发育长宁背斜，构造较为简单，构造轴呈北西西—南东东向，西南翼较平缓，东北翼较陡。受多期构造运动影响，研究区主要发育北东—南西向和近东西向2 组断裂体系，均为逆断层，且以中小断层为主，多数消失在志留系内部。主要目的层为上奥陶统五峰组—下志留统龙马溪组龙一1 亚段，埋深为1 500～4 000 m，构造高部位及南翼埋深普遍小于3 500 m，向构造以北和以西埋深逐渐增大（图2），地层倾角为15°～60°。目的层厚度为36～48 m，岩性为一套富有机质黑色碳质页岩，页理发育，富含大量笔石化石，含黄铁矿结核和条带。龙一1 亚段被认为是最有利于页岩气富集的优质页岩段，根据岩性、沉积构造、生物化石和电性特征，将其划分为4 个小层[17-18]，自下而上依次为龙一11小层、龙一12小层、龙一13小层和龙一14小层（图3）。

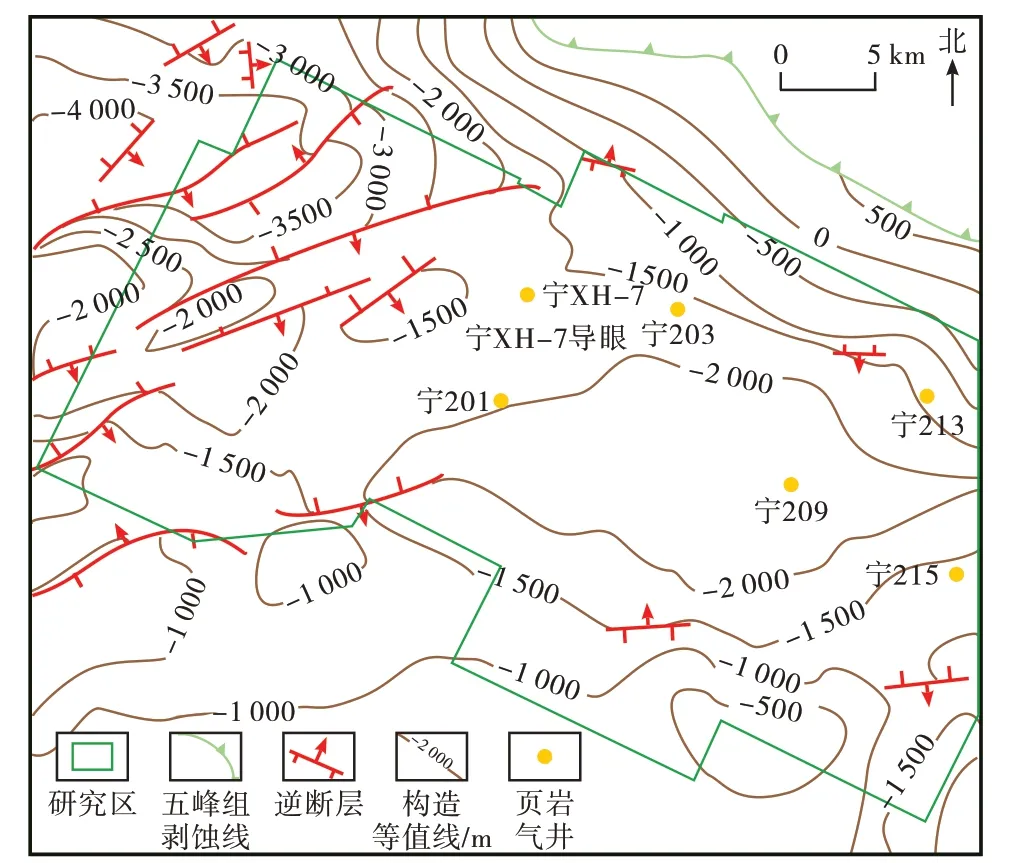
图2 研究区五峰组顶界构造Fig.2.Top structure of the Wufeng formation in the study area

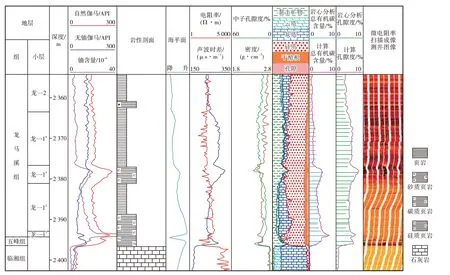
图3 研究区龙一1亚段小层划分、岩性、沉积相及电性特征Fig.3.Layers,lithology,sedimentary facies and electrical properties of Long11 in the study area

研究区五峰组—龙一1 亚段储集层孔隙度为4.0%～7.5%，其中龙一11小层储集性能最好，龙一13小层次之，五峰组和龙一14小层相当，龙一12小层最差。五峰组—龙一1 亚段在各井、各小层之间岩心分析孔隙度存在较大差异，说明页岩层储集性能有一定变化，总体以宁201 井最优，其次为宁XH-7 导眼井，宁213 井最差（图4）。经直井岩心标定，研究区测井孔隙度模型计算孔隙度误差小于10%，满足直井储量和储集层分级要求。但研究区采用水平井开发，水平段长度为1 500～2 500 m；由于各向异性的影响，水平井纵波时差比直井小，差异最大可达60 μs/m，计算孔隙度相对误差超过30%，导致页岩储集层划分和储量评价误差大，采用大斜度井及水平井垂向纵波时差计算的长宁页岩气开发示范区储集层孔隙度，更符合实际地质情况。

图4 研究区五峰组—龙一1亚段各小层孔隙度对比Fig.4.Sublayer porosities of Wufeng formation-Long11 in the study area

3.2 纵波时差计算孔隙度

四川盆地长宁页岩气开发示范区龙马溪组测量的纵波时差在同层段存在明显的差异（图5），宁XH-7 井与宁XH-7 导眼井2 050—2 040 m 井段的纵波时差差异随井深变化从0 逐渐增大至60 μs/m；2 口井水平位移从0 增加到380 m，邻近的其他直井纵向上的纵波时差为200～300 μs/m，与宁XH-7 导眼井相同，邻近直井同层段横向纵波时差变化小于10 μs/m。区域研究表明，页岩储集层分布稳定，储集层岩性、物性横向变化小[19-20]，显然纵波时差差异高达60 μs/m 与岩性、物性变化规律不符，不是岩石组分和物性差异所导致。分析井斜角与纵波时差差异发现，纵波时差差异随着井斜角变大而变大，认为长宁页岩气开发示范区纵波在垂向和水平方向传播时存在明显的各向异性，测量纵波时差受井斜角影响严重。

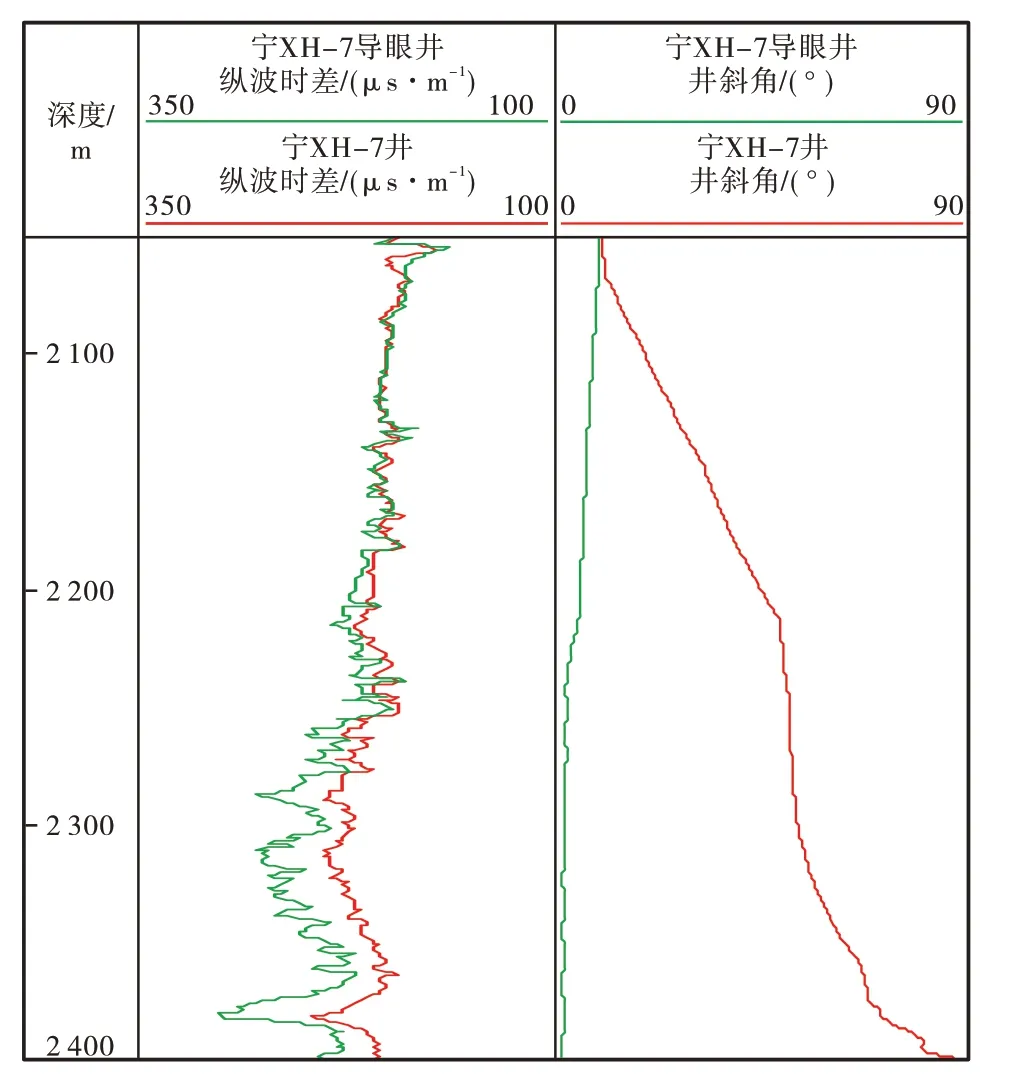
图5 宁XH-7导眼井与宁XH-7井纵波时差和井斜角对比Fig.5.P⁃wave slowness and well deviation of Ning XH⁃7 guide well and Ning XH⁃7 well

因此，用纵波时差、直井岩心标定和刻度的储集层参数模型来评价大斜度井及水平井储集层物性，要先消除井斜角和各向异性对纵波时差的影响，研究垂向和水平方向纵波时差的计算方法。在同一钻井平台，测量直井、大斜度井和水平井同层位的纵波时差，确定纵波时差与井斜角的关系，获得垂向纵波时差。

由于页岩骨架矿物组成在纵向上变化较大，且开发井资料有限，采用多元约束响应方程求解不能获得高精度的孔隙度，而计算孔隙度的影响因素多，难于区分其误差来源，计算孔隙度与岩心分析孔隙度误差较大。因此，在孔隙度比较中，采用研究区多口关键井岩心分析孔隙度与测井资料建立的模型计算页岩孔隙度[21]：

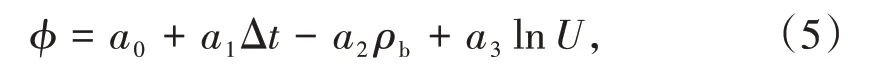
式中a0、a1、a2、a3——岩心标定系数；

U——铀含量，10-6；

ϕ——孔隙度，%；

ρb——测井密度，g/cm3。

对直井和水平井测井资料进行井斜校正后，以直井为参考，对测井资料按照地层进行深度标定，用直接拟合法和各向异性椭圆模型法计算垂向纵波时差和水平纵波时差，用（5）式计算孔隙度（图6），直接拟合法和各向异性椭圆模型法计算纵波时差与直井测量纵波时差对比可以得出：水平井测量纵波时差与直井测量纵波时差存在明显差异，各向异性椭圆模型法计算垂向纵波时差与直井测量纵波时差的差异比直接拟合法计算垂向纵波时差与直井测量纵波时差的差异小，而且各向异性椭圆模型法计算垂向纵波时差在形态和数值上与直井更为一致，直接拟合法和各向异性椭圆模型法计算垂向纵波时差计算孔隙度与直井孔隙度比较，各向异性椭圆模型法得到的孔隙度更为准确。龙一1 亚段垂深为2 375—2 400 m，对直井和水平井计算的孔隙度进行对比（表1），水平井测量纵波时差与直井测量纵波时差计算孔隙度相对误差高达32.2%，直接拟合法和各向异性椭圆模型法计算垂向纵波时差计算孔隙度与直井孔隙度的相对误差分别为7.8%和2.1%，说明水平井测量纵波时差不适合用于计算页岩储集层孔隙度，直接拟合法和各向异性椭圆模型法提高了纵波时差计算水平井页岩储集层孔隙度的精度，各向异性椭圆模型法精度更高。各向异性椭圆模型法计算垂向纵波时差方法在长宁页岩气开发示范区大斜度井及水平井孔隙度评价中得到广泛应用，其评价结果符合地质规律，与开发生产情况具有较好的可对比性。

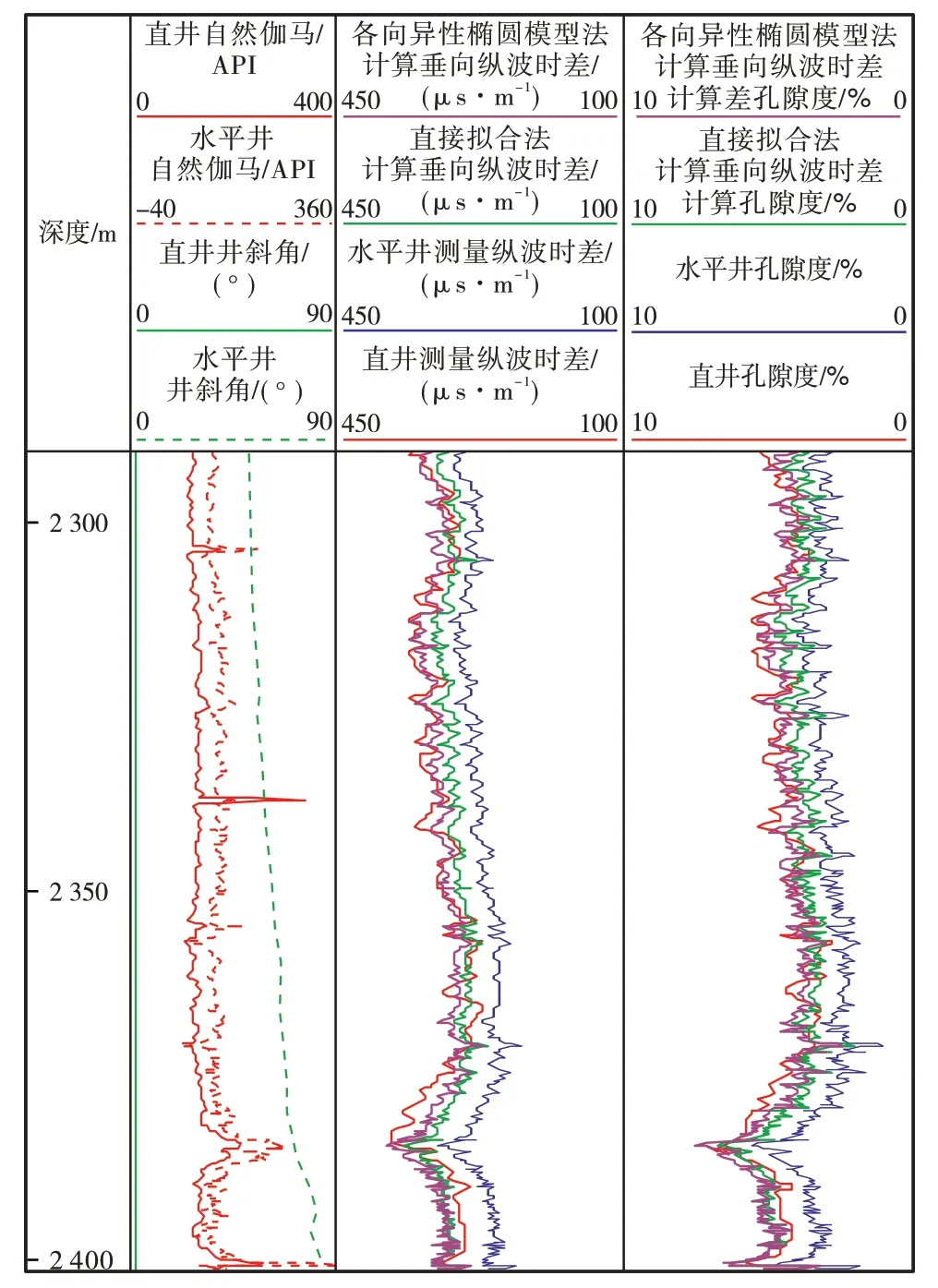
图6 研究区不同方法计算垂向纵波时差及孔隙度对比Fig.6.Vertical P-wave slowness and porosity calculated with dif⁃ferent methods in the study area

表1 研究区龙一1亚段直井与水平井计算孔隙度及相对误差Table1.Porosities and relative errors of vertical and horizontal wells in Long11 in the study area

4 结论

（1）大斜度井及水平井测量纵波时差因传播速度的各向异性受井斜角影响严重，采用直井岩心标定的孔隙度模型评价页岩储集层孔隙度误差大，需要对测量纵波时差进行各向异性及井斜校正，得到垂向纵波时差，才能满足孔隙度评价的精度要求。

（2）采用直接拟合法和各向异性椭圆模型法获得水平井垂向纵波时差，利用区域直井建立的孔隙度模型计算大斜度井及水平井地层的孔隙度与同平台直井误差分别为7.8%和2.1%，均满足储集层评价对孔隙度的需求，且各向异性椭圆模型法计算结果精度更高，更加符合地质认识规律。

（3）各向异性椭圆模型法通过邻近的直井、大斜度井、水平井同层段纵波时差和井斜角计算水平纵波时差和垂向纵波时差，完全依赖测井资料，方法简便、适用性强、精度更高，在评价长宁页岩气开发示范区水平井储集层孔隙度中得到广泛的应用，为页岩储集层综合评价和开发生产提供了更为准确的物性依据。