基于变分模态分解和改进粒子群算法优化最小二乘支持向量机的短期电价预测

杨 昭 张 钢 赵俊杰 张 灏 蔺奕存

基于变分模态分解和改进粒子群算法优化最小二乘支持向量机的短期电价预测

杨 昭 张 钢 赵俊杰 张 灏 蔺奕存

（西安热工研究院有限公司，西安 710054）

针对电价序列具有非线性强、波动性大的特点，提出一种基于变分模态分解（VMD）和改进粒子群算法（PSO）优化最小二乘支持向量机（LSSVM）的短期电价预测模型。首先利用VMD将原始电价数据分解为多个子序列，然后采取LSSVM模型分别对子序列进行预测。对于LSSVM预测模型的最优参数选择问题，利用改进的PSO优化LSSVM模型的参数，能够很好地提高模型预测精度。最后集成各子序列预测结果，获得最终电价预测值。为了验证所提模型的有效性，以美国PJM市场电价数据为例进行分析，并与其他预测模型进行对比，结果表明，所提模型能够很好地对短期电价进行预测。

电价预测；变分模态分解；粒子群算法；最小二乘支持向量机

0 引言

在我国当前开放电力市场背景下，电价作为电力市场的支点，能够直接影响各个市场参与主体的经济效益。电力市场也作为一个拍卖市场，使得电价具有波动性，故各市场参与者可以利用电价预测很好地去规避波动[1-2]。

电价的预测受历史电价、负荷需求、天气等因素的影响。有国内学者研究不同输入参数对电价预测的影响，从预测结果发现，历史电价自身就能够体现出其他参数的影响，加入其他因素对最终预测结果影响甚微，甚至会降低预测效果[3]。本文对短期电价进行预测时仅考虑历史电价作为输入。

本文对短期电价预测的输入参数只选取历史电价。多年来，国内外学者提出了大量优秀的组合电价预测模型，比如时间序列组合模型、人工智能算法组合模型、时间序列及智能算法组合模型[4-8]。由于原始电价序列具有很强的非线性及不平稳性，仅使用上述模型不易捕捉到原始电价序列特性，也会影响电价的预测精度。因此，对原始电价进行“分解”处理至关重要。当前，基于“分解—预测—集成”的预测模型是广大学者研究的重点。文献[9]利用集合经验模态分解（ensemble empirical mode decom- position, EEMD）将原始数据序列分解为多个平稳分量，再选取最小二乘支持向量机（least square support vector machine, LSSVM）对各子序列进行预测并集成；文献[10]通过经验模态分解（empirical mode decomposition, EMD）对原始风功率数据进行分解；文献[11]通过互补集合经验模态分解（complementary ensemble empirical mode decomposition, CEEMD）进行原始电价序列分解；文献[12-13]对原始数据序列进行小波处理，再利用粒子群优化（particle swarm optimization, PSO）算法后的最小二乘向量机对各分量进行预测并集成；文献[14]利用快速集合经验模态分解（fast ensemble empirical mode decomposition, FEEMD）对原始电价序列进行分解，再采取鲸鱼优化算法（whale optimization algorithm, WOA）-径向基函数（radial basis function, RBF）对分解后的分量序列进行预测。这种“分解—预测—集成”方法被证实确实可以提升预测精度。然而上述研究有些许不足，比如对原始数据进行小波处理时需提前设置小波基函数、分解层数，不具有自适应特性；EMD后的模态数目不能提前设定，同时，EMD、EEMD等分解方法在分解过程中存在模态混叠问题，导致分解结果也不理想。目前，变分模态分解（variational mode decomposition, VMD）是一种具有自适应、完全非递归的模态变分分解方法，能够避免其他分解方法分解后存在的模态混叠及端点效应现象，对于非线性强、波动剧烈的数据序列，有很明显的处理优势。

本文提出一种基于VMD-改进粒子群算法优化LSSVM的电价预测模型。针对原始电价序列波动剧烈的特点，首先利用VMD将原始电价序列分解为多个平稳的模态分量，然后采用改进PSO-LSSVM模型对各个分量序列进行预测，最终对各分量集成得到总预测输出。选取美国PJM市场的真实电价数据进行验证，结果表明，VMD-改进PSO-LSSVM模型能够很好地对短期电价进行预测，有较高的精度。

1 短期电价预测模型

基于VMD-改进PSO-LSSVM短期电价预测模型采取“分解—预测—集成”的预测思想，其模型如图1所示，主要步骤为：

1）采取VMD方法对原始电价序列实现分解，得到个分量{1,2,…,U}。

2）采取中心频率法确定，将频率值接近的分量视为相似模态分量，获取原始数据经VMD后不同中心频率对应的不同分量。

3）对于分解后的各子分量，实现LSSVM建模。由于LSSVM中的两个参数能够很大程度影响模型的精度，采用改进PSO对参数进行寻优，选择优秀的性能参数，提升模型预测的精度。

4）对各个分量的预测结果进行集成获得最终的总预测输出，并通过评价指标和其他模型进行比对，分析本文所提预测模型的性能。

图1 基于VMD-改进PSO-LSSVM短期电价预测模型

2 基于VMD的原始电价时间序列分解

2.1 VMD

VMD是Dragomiretskiy等提出的一种自适应、完全非递归的模态变分及信号处理方法[15-16]。VMD的核心思路是构建和求解变分问题，将一个输入信号解耦为一组离散的、有限带宽的模态函数集合，按照信号的频域特性实现输入信号的自适应分解[17-18]。主要流程如下：

1）利用Hilbert变换获取U的解析信号，得到单边频谱。

3）通过高斯平滑度和梯度二次方准则对信号解调，计算梯度的二次方L2范数，获得各分解模态的带宽。分解后的各模态量变分约束模型为

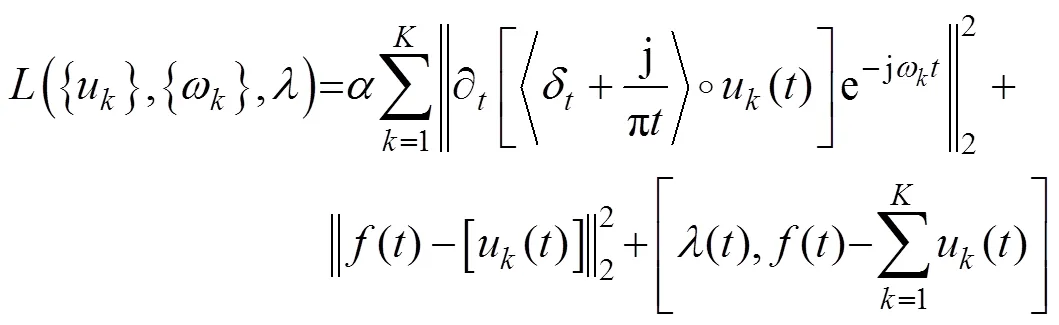
2.2 VMD参数的确定

1）模态个数

经VMD后的子序列数目的选择至关重要，值过小会引起分解不足问题，最终降低预测精度；值过大会产生模态重复问题。一般选择3～8个 即可。

2）惩罚因子

标准VMD考虑模态混叠与收敛速度的问题，普遍选取惩罚因子为2 000，具有高适应性。本文惩罚因子也采用2 000。

3 基于改进PSO-LSSVM的预测模型

3.1 最小二乘支持向量机

LSSVM是对传统SVM的改进，将SVM中的不等式约束线性化，避免了二次规划问题，很大程度地提升了运行速度和计算精度[19]。

LSSVM优化函数为

3.2 改进粒子群算法参数优化原理

对于标准粒子群算法来说，改进粒子群算法的思想[20]是引入一个互斥的过程，在粒子不停迭代期间，达成粒子间吸引和排斥的平衡状态，避免粒子早熟收敛。当粒子间的距离和适应度方差均小于事先给定的阈值时，再次调整各个粒子在解空间的位置，维持种群的活跃性，提升粒子搜索的多面性。引入两个多样性指标对PSO进行改进。

1）选取初始种群

引入平均粒距概念，即

2）判断早熟收敛

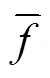
式中，为归一化定标因子，有

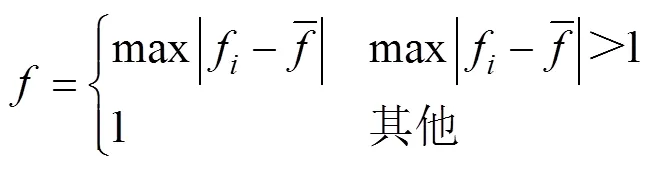
3.3 组合模型的构建

组合模型构建流程如图2所示，改进PSO-LSSVM模型实现步骤如下：

图2 组合模型构建流程

1）粒子群初始化，设定种群规模，惯性权重初值、终值max、min，加速常数1、2，迭代次数max。

4）对粒子种群重新初始化。

5）更新各粒子速度与位置，得到新粒子种群，记为()。

7）判断是否达到终止条件，迭代完成或适应度值符合要求，输出最优解，否则转步骤2）。

4 算例分析

4.1 数据来源及数据分解

为验证本文预测模型进行短期电价预测的有效性，选择美国PJM市场2016年1月1号至2016年1月31号的历史电价数据为研究对象，采样间隔为1h，31天共744个电价数据点，历史电价数据如图3所示。通过VMD对原始电价数据进行分解，分解结果如图4所示。

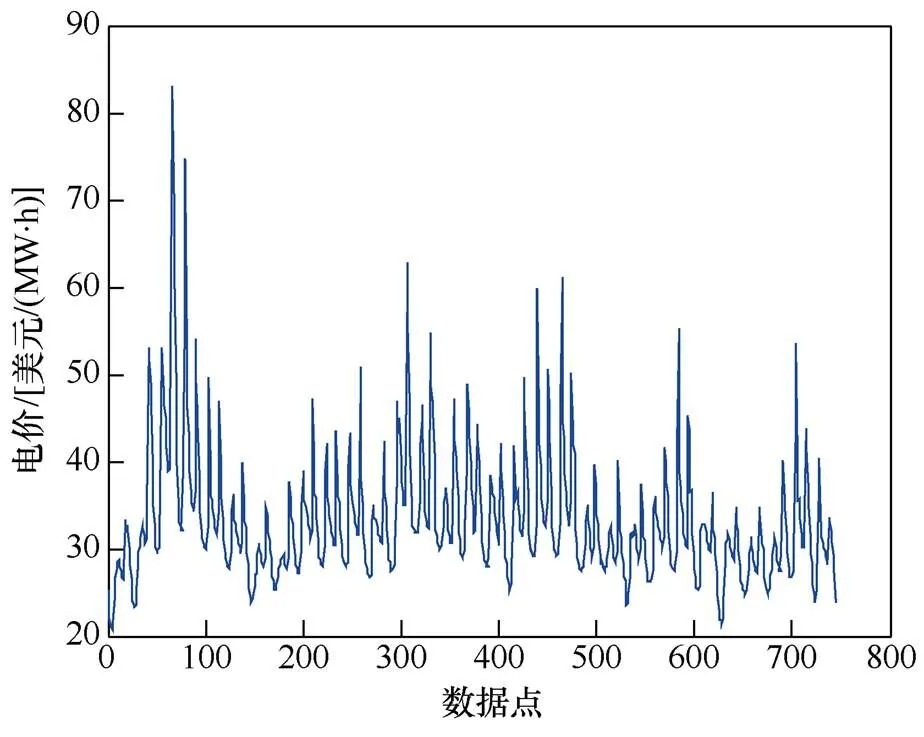
图3 历史电价数据

4.2 结果分析

将744个数据分为训练样本和测试样本，其中前26天电价数据作为训练样本，最后5天的120个电价数据作为测试样本，验证本文提出的短期电价预测模型的性能。设定粒子数目为20，迭代次数max为100，平均粒距阈值取0.01，适应度方差阈值取0.01。电价预测结果如图5所示。

图4 VMD结果

图5 电价预测结果

由图5可知，本文所提出模型的拟合结果比较理想。除了区间0～24有较明显的偏差，预测值低于实际值，可能是由于当天存在某些特殊因素，比如机组检修、市场电量需求减少引起的，其他时间预测值和实际值很接近，误差最小能达到0。

为了进一步验证本文所提模型的有效性，将EMD、PSO、LSSVM组合预测模型、PSO-LSSVM模型、LSSVM模型和本文模型进行对比，各模型预测结果如图6所示。选取平均绝对误差（mean absolute error, MAE）、方均根误差（root mean square error, RMSE）和平均绝对百分比误差（mean absolute percentage error, MAPE）为评价指标，各模型预测性能对比见表1。

图6 各模型预测结果

表1 PJM市场各模型预测性能对比

由表1可知，组合预测模型的精度明显高于单个模型。本文模型比单个LSSVM模型的MAE提高了1.174 3美元/(MW·h)，RMSE提高了1.688 5美元/(MW·h)，MAPE提高了3%，很好地克服了单一预测模型的不足。同时能够反映出，预测前对原始数据进行分解、分别预测再进行集成的预测方法优于直接利用原始数据序列进行预测的模型，提升效果也较显著。

5 结论

本文提出基于VMD-改进PSO-LSSVM的组合模型对短期电价进行预测。首先利用VMD对波动性大、非线性强的原始电价数据进行分解；然后利用改进PSO-LSSVM算法对VMD后的各子分量序列进行预测，最后对各分量预测结果进行集成得到最终电价预测值。为了验证本文所提模型的有效性，选取美国PJM市场的电价数据进行短期预测。实例结果表明，改进PSO能够很好地优化LSSVM模型参数，组合预测模型明显优于单一预测模型。通过预测性能评价指标能够很直观地说明本文所提出的“分解—预测—集成”模型能够对短期电价进行有效预测。本文所提出的组合预测模型可以推广至负荷预测、风速预测等多方面。

本文模型的不足在于：当存在某些特殊情况时，电价预测效果欠佳。在后续的研究中，综合考虑多因素进行建模，比如天气、节日等，对短期电价进行综合预测。

[1] 魏勤, 陈仕军, 黄炜斌, 等. 利用随机森林回归的现货市场出清价格预测方法[J]. 中国电机工程学报, 2021, 41(4): 1360-1367, 1542.

[2] 赵雅雪, 王旭, 蒋传文, 等. 基于最大信息系数相关性分析和改进多层级门控LSTM的短期电价预测方法[J]. 中国电机工程学报, 2021, 41(1): 135-146, 404.

[3] 刘威. 互联电力市场的区域电价预测[D]. 武汉: 华中科技大学, 2018.

[4] 周明, 严正, 倪以信, 等. 含误差预测校正的ARIMA电价预测新方法[J]. 中国电机工程学报, 2004, 24(12): 67-72.

[5] 殷豪, 曾云, 孟安波, 等. 基于奇异谱分析的短期电价预测[J]. 电力系统保护与控制, 2019, 47(1): 115- 122.

[6] 任远. 基于回声状态网络的电力市场电价预测[J]. 电力系统保护与控制, 2016, 44(11): 111-115.

[7] 何耀耀, 刘瑞, 撖奥洋. 基于实时电价与支持向量分位数回归的短期电力负荷概率密度预测方法[J].中国电机工程学报, 2017, 37(3): 768-776.

[8] 李鹏, 何帅, 韩鹏飞, 等. 基于长短期记忆的实时电价条件下智能电网短期负荷预测[J]. 电网技术, 2018, 42(12): 4045-4052.

[9] 王贺, 胡志坚, 张翌晖, 等. 基于聚类经验模态分解和最小二乘支持向量机的短期风速组合预测[J]. 电工技术学报, 2014, 29(4): 237-245.

[10] 夏书悦, 董心怡. 基于经验模态分解法优化支持向量机模型的日前风电功率组合预测[J]. 电气技术, 2020, 21(3): 11-15.

[11] 张宁. 基于CEEMD-SSA-ELM的短期电价集成预测模型[J]. 贵州大学学报(自然科学版), 2020, 37(5): 82-88.

[12] 田中大, 李树江, 王艳红, 等. 基于小波变换的风电场短期风速组合预测[J]. 电工技术学报, 2015, 30(9): 112-120.

[13] 叶瑞丽, 郭志忠, 刘瑞叶, 等. 基于小波包分解和改进Elman神经网络的风电场风速和风电功率预测[J]. 电工技术学报, 2017, 32(21): 103-111.

[14] 蒋锋, 何佳琪, 曾志刚, 等. 基于分解-优化-集成学习方法的电价预测[J]. 中国科学(信息科学), 2018, 48(10): 1300-1315.

[15] 王俊, 李霞, 周昔东, 等. 基于VMD和LSTM的超短期风速预测[J]. 电力系统保护与控制, 2020, 48(11): 45-52.

[16] ZHANG Gang, LIU Hongchi, LI Pingli, et al. Load prediction based on hybrid model of VMD-mRMR- BPNN-LSSVM[J]. Complexity, 2020(4): 6940786.

[17] 杨晶显, 张帅, 刘继春, 等. 基于VMD和双重注意力机制LSTM的短期光伏功率预测[J]. 电力系统自动化, 2021, 45(3): 174-182.

[18] 余向阳, 赵怡茗, 杨宁宁, 等. 基于VMD-SE-LSSVM和迭代误差修正的光伏发电功率预测[J]. 太阳能学报, 2020, 41(2): 310-318.

[19] 赵倩, 陈芳芳, 甘露. 基于改进粒子群算法优化支持向量机的风电功率预测[J]. 电气技术, 2020, 21(12): 12-16.

[20] 范曼萍, 周冬. 基于改进粒子群优化LS-SVM的短期风速预测[J]. 电力学报, 2020, 35(2): 123-128, 142.

Short term electricity price forecasting based on variational mode decomposition and improved particle swarm optimization-least square support vector machine

YANG Zhao ZHANG Gang ZHAO Junjie ZHANG Hao LIN Yicun

(Xi’an Thermal Power Research Institute Co., Ltd, Xi’an 710054)

According to the characteristics of strong non-linearity and high volatility of electricity price series, a short-term electricity price prediction model based on variational mode decomposition (VMD) and least square support vector machine (LSSVM) optimized by improved particle swarm optimization (PSO) is proposed. First of all, VMD is used to decompose the original electricity price sequence into multiple component sequences, and LSSVM modeling and prediction is performed on each component sequence. And then, in order to improve the prediction accuracy, aiming at the problem of selecting the optimal parameters of the LSSVM prediction model, an improved particle swarm algorithm is proposed to optimize the parameters of the LSSVM model. Finally, the prediction results of each component are integrated to obtain the final electricity price prediction value. In order to verify the effectiveness of the proposed model, the US PJM market electricity price data is used as an example to analyze and compare with other forecasting models. It shows that the proposed model can predict short-term electricity prices well.

electricity price forecasting; variational mode decomposition (VMD); particle swarm optimization (PSO); least square support vector machine (LSSVM)

2021-03-10

2021-04-09

杨 昭（1996—），男，硕士，助理工程师，从事发电厂电气起动调试工作。