尘埃等离子体中扩展的ZK方程的最优系统和幂级数解

高 芳

(聊城大学 数学科学学院，山东 聊城 252059)

0 引言

李对称分析是非线性偏微分方程求解的方法之一，其思想是通过构造不变量作为函数变换的基础，使偏微分方程减少一个自变量得到化简或求解。比如，文献[1]研究了耦合可积无色散方程，在李对称分析的基础上，构造了一维子代数的最优系统，给出了相似约简和群不变解，并且得到了显示幂级数解和方程的守恒律；文献[2]也同样应用经典对称方法研究了双曲曲线流演化方程对称性的一维最优系统，精确解和幂级数解；文献[3]还用同样方法讨论了带耗散性的正双曲平均曲率流的群不变解和幂级数解以及幂级数解的收敛性。

最近，多位学者研究了尘埃等离子体和量子物理中的非线性Zakharov-Kuznetsov(ZK)型方程。文献[4]研究了超热电子-正电子-离子等离子体中的Zakharov-Kuznetsov-Burgers方程;文献[5]利用约化微扰法，导出了离子声孤波的非线性ZK方程;文献[6]研究了具有上自旋和下自旋电子相对密度效应的磁化量子等离子体中的非线性静电孤立脉冲;文献[7]探讨了磁化尘埃等离子体中三维非线性扩展ZK动力学方程的声孤波解。

高东宁等[8]提出了扩展的ZK方程

ut-ux+Auux+Bu2ux+Cuxxx+D(uxyy+uxzz)=0,

(1)

其中A,B,C,D定义于文献[8]中。Shrouk Weal等[9]研究了方程(1)的对称约化、守恒律和声波解，通过李群分析得到6个李代数生成子如下：

(2)

基于上述研究成果，拟应用(2)式和李对称方法，研究扩展的方程(1)的最优系统、精确解和幂级数。

1 一维最优系统

令(1)(2)式中的系数A=-2，B=-1,(1)式变为

ut-ux-2uux-u2ux+Cuxxx+D(uxyy+uxzz)=0,

(3)

则(2)变为

(4)

根据(4)式和公式

[Vi,Vj]=ViVj-VjVi,

可以得到李括号表，见表1。

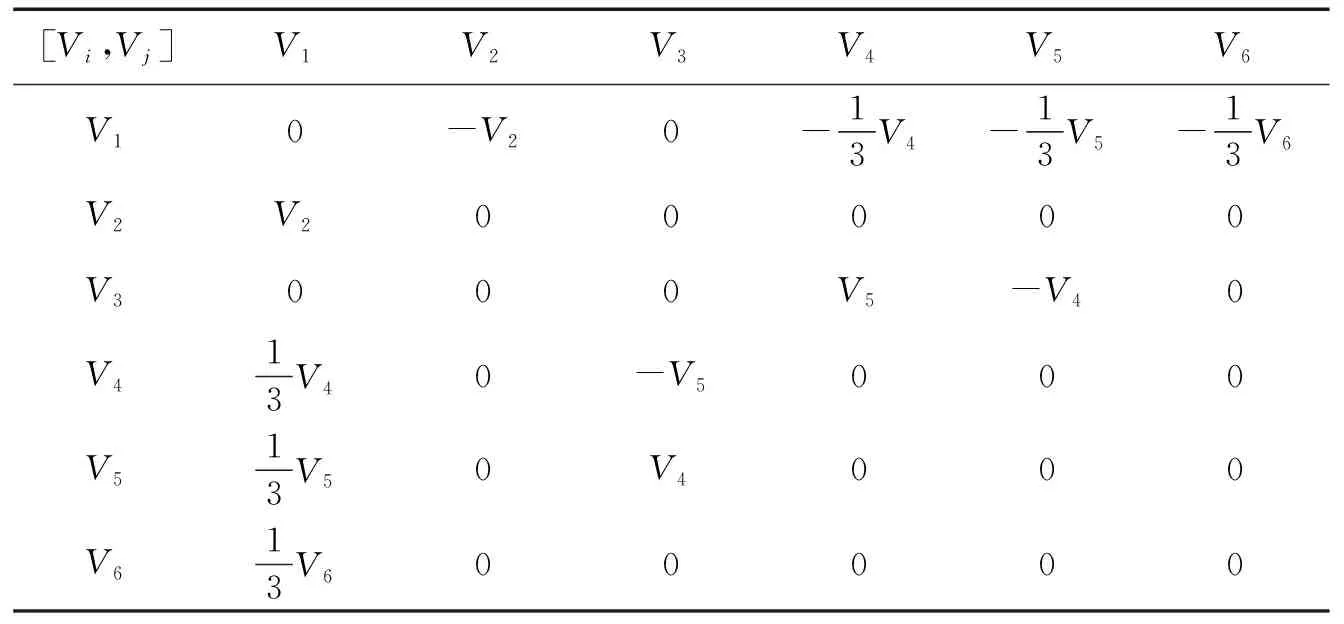
表1 李括号表

假设任一向量

V=l1V1+l2V2+l3V3+l4V4+l5V5+l6V6,

(5)

建立线性变换

(6)

令

(7)

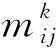
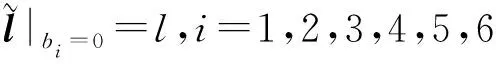
(8)

(8)式的解构成变换

为了求得最优系统，需要化简向量(6):

情况(a) 如果l1≠0,令

使得

则向量(6)等价于(l1,0,l3,0,0,0),则V等价于V1±V3,V1。

情况(b) 如果l1=0,则向量(6)等价于(0,l2,l3,l4,l5,l6),分为两种情况：

(b-1) 如果l3≠0,令

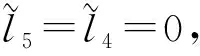
(b-2) 如果l3=0,则向量(6)等价于(0,l2,0,l4,l5,l6),又分为两种子情况：

(b-2-1) 如果l5≠0,令

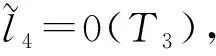
(b-2-2) 如果l5=0,此时向量(6)等价于(0,l2,0,l4,0,l6),V等价于V2±V4±V6,V4±V6,V2±V6,V2±V4,V6,V4,V2。

因此，得到一个最优系统

{V1,V2,V3,V4,V5,V6,V1±V3,V2±V4,V2±V6,V3±V2,V3±V6,V4±V6,V5±V6,

V5±V2,V5±V2±V6,V3±V2±V6,V2±V4±V6}。

2 精确解

解特征方程得到不变量为

Y=y,Z=z,X=x-t,

不变解为u=M(X,Y,Z),代入方程(3),得到

-2MX-2MMX-M2MX+CMXXX+D(MXYY+MXZZ)=0。

(9)

对方程(9)进行李对称分析，得到方程(9)的向量

因此，得到4个生成子

令

则不变解为

M=f(Z,h),h=X-Y,

代入(9)式得到

解特征方程得到不变量为

X=x,Y=y2+z2,T=z+yt,

不变解为u=N(X,Y,T),代入方程(3),得

yNT-NX-2NNX-N2NX+CNXXX+D(4NXY+4YNXYY+4TNXTT+(t2+1)NXTT)=0。

(10)

解特征方程得到不变量为

T=t,Z=z,X=x-y,

不变解为u=H(X,Y,Z),代入方程(3),得到

HT-HX-2HHX-H2HX+CHXXX+D(HXXX+HXZZ)=0。

(11)

方程(11)的李对称由无穷小生成子

得到李代数生成子

令

则不变解为

H=S(T,h),h=X-Z,

代入(11)式得到

ST-Sh-2SSh-S2Sh+(C+2D)Shhh=0。

(12)

对方程(12)再次进行李对称分析和对称约化后得到不变解为

S=f(φ)=f(T-h)，

2f′+2ff′+f2f′-(C+2D)f‴=0。

(13)

3 幂级数解

应用幂级数方法研究方程(13)幂级数解的构成如下：

(14)

其中pn是未知系数。

把(14)式代入方程(13)，得

(15)

比较方程(15)的系数，当n≥0时，

(16)

根据(16)式可以得到(14)式中所有的系数pi(i≥2),

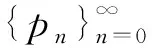
关于(16)式，有

其中

定义幂级数

显然

|pn|≤rn,n=0,1,2,…

因此，级数R=R(φ)是级数(14)的优级数，则R=R(φ)有正的收敛半径。

考虑关于独立变量φ的隐函数

因为F在(φ,R)面上是解析的，并且

F(0,r0)=0,FR′(0,r0)=1≠0,

应用隐函数定理[10]得出，在点(0,r0)的一个邻域内，R=R(φ)是解析的，并且有正的半径。即意味着，在平面上的点(0,r0)邻域内，幂级数(14)收敛。

因此，方程(13)的幂级数解(14)是解析的，形如：

因此，方程(3)的显示幂级数解为

u=u(x,y,z,t)=p0+p1(-x+y+z+t)+p2(-x+y+z+t)2+

4 结论

基于李对称方法研究了尘埃等离子体中扩展的Zakharov-Kuznetsov方程，首先得到了方程的一维最优系统，然后解得了方程的精确解，最后应用幂级数方法得到了方程的显示解。