基于NPU的光纤振动信号数据预处理算法

郭家旭，董 雷

（1.武汉邮电科学研究院，湖北武汉 430000；2.武汉理工光科股份有限公司，湖北武汉 430000）

光纤周界安防系统中的定位型振动光纤入侵探测系统是基于相位敏感的光时域反射技术[1]，它能够探测传导至光纤上的振动信号，经过信号处理和模式识别，可定位具体的入侵信息，且具有探测距离长[2-5]的优点，多应用于周界入侵探测。定位型振动光纤入侵探测主机输出巨大的传感器阵列信号，数据量很大，但需要进行模式识别的只是运算后的几个特征量[6]。特征量由数据的预处理完成，在进行信号数据的预处理过程中，需要对矩阵进行卷积和平方及四次方这种逻辑简单但计算量大的运算，运算过程在通用CPU(Central Processing Unit)端计算时间长而且特别消耗计算资源[7]，在实时检测的过程中，占有率通常大于90%。为了进一步提升性能，文中利用华为公司生产的NPU（Neural Network Processing Units）设 备Atlas200DK实现对定位型光纤振动入侵探测主机产生的原始解调数据进行预处理，以此分担CPU 端的运算压力。

1 TensorFlow及NPU设备简介

TensorFlow 是一个使用数据流以计算图的方式进行数值计算的开放源代码软件库，支持C/C++、Python 等编程语言[8]。计算图指定了各个变量之间的计算关系，图中的每个节点代表数学运算操作，节点与节点之间的连接叫作边，边代表在这些节点之间传递的数据。TensorFlow 不仅仅为实现机器学习或深度学习提供算法接口，同时它也是执行机器学习算法或深度学习算法进行计算的框架。计算图一般被组织成构建阶段和执行阶段[9]。在构建阶段，用张量来描述各节点的操作并把它们连接起来，此时的计算图只是一个空壳，没有任何输出。在执行阶段，使用会话执行图中的各个节点，将需要计算的具体数据传入计算图中进行计算并输出计算结果。

不同于传统的支持通用计算的CPU 和图形处理器(Graphics Processing Unit，GPU)，华为公司专门研发了一款基于达芬奇架构[10]的NPU芯片，这种架构是为了适应某个特定领域中的常见应用和算法。一般来说，GPU 要通过矩阵计算来实现卷积，这一步骤需要通过软件来实现[11]。该NPU芯片采用了一个专用的存储转换单元来完成这一过程，将这一步完全固化在硬件电路中，可以在很短的时间之内完成整个转置过程。由于类似转置的计算在深度神经网络中出现得极为频繁，这样定制化电路模块的设计可以提升执行效率，从而能够实现不间断的卷积计算。文中实验所使用的NPU 设备是一款专门为深度学习的运算和部署设计的移动小型设备。

2 数据的预处理

2.1 在CPU端实现数据的预处理

系统采集到的数据是对一根传感光纤不断进行扫描得来的。由于光纤的长度是一定的，因此光纤上分布的传感器数量也是固定的，得到的数据是一个列数一定、行数不断增加的动态二维矩阵。在实际处理中，每次选取其中某一时间片段进行处理。系统的采样频率为400 Hz，在截取片段时只截取1 s的数据，即每秒调用一次预处理程序来处理400 个周期的数据。

入侵振动信号通常是一个突变量，主要信息常常集中在20～120 Hz 部分，但是由于激光器、光路、硬件电路以及环境等因素引入的低频和其他分量会造成低频漂移或其他现象，对特征信号后续的识别带来了一定的影响。所以系统采集的原始数据在后续求包络时不能直接使用，一般使用高通滤波器去除20 Hz 以下的分量[12-13]，文中实验使用带通滤波器提取出20～100 Hz的振动信号，使系统能够提取出有效的振动信息。

一般来说，在判别是否有异常入侵事件以及类型时，判决器需要根据预处理后得到的峰度和包络两个特征量来进行异常模式的识别和定位。预处理流程如图1 所示。

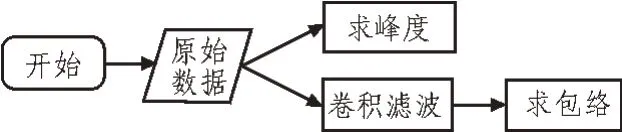
图1 预处理流程

峰度是描述一组数据分布的平坦度，表征概率密度分布曲线在平均值处峰值高低的特征数，反映了峰部的尖度，一般用四阶中心矩[14]来表示。在实验中，利用峰度值来判定振动发生的位置，其公式为：

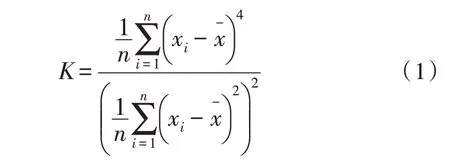
峰度计算流程如图2 所示。

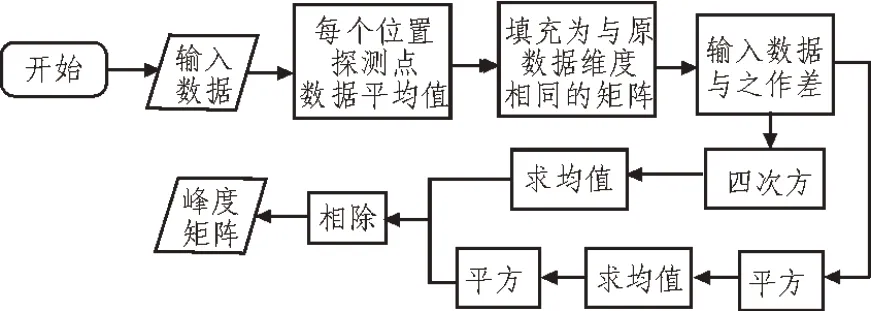
图2 峰度计算流程

包络是另一个判定振动的特征量，它是自定义的。滤波后的数据较难提取出相邻两次激励的间隔，而利用包络可以清晰得出结果，方便判断振动类型，生成的瀑布图可以更直观地看出振动位置、振动发生的地点以及相对强度。为了减少计算量，一般对时间点的维度进行分组[15-16]，求出每个传感器所对应该段时间内的最大值和最小值的差，得到一个一维矩阵，即该段时间内的包络数据。包络计算流程如图3 所示。

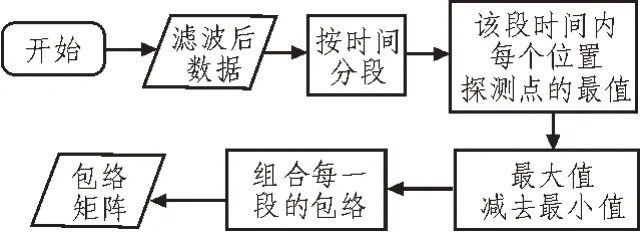
图3 包络计算流程

由于Matlab 对于矩阵运算十分友好且代码结构简单，因此系统在CPU 端进行预处理时调用Matlab的库文件对数据进行运算。本地数据为一段光纤中10 000 个光纤位置采样点和这10 000 个位置采样点的13 200 个时间采样点组成的13 200×10 000的double 型的二维矩阵。为了减少计算时间，方便说明算法流程，在实验中，具体算法只计算了400 个时间采样点，即1 s的数据，在读取时先读取500 个时间采样点的数据。

在滤波操作中，数字滤波器原理简单，且在Matlab 上使用卷积滤波来实现带通滤波器的功能较为容易，只需使用自带的一维线性滤波器filter，具体代码如下：

Buf_data_filte=filter(obj.Num,1,Buf_data_o)

其中，Buf_data_filter 为卷积滤波后的数据，obj.Num 为卷积滤波器的系数，Buf_data_o 为读取的原始数据。

为了减少滤波时突变信号对后续计算包络所产生的影响，在实际处理中，选取滤波后500 个时间采样点中去掉两端后的400 个时间采样点的数据。通常情况下，系统通过判断峰度值的大小来判断振动发生的位置，数值大于7 即为发生了振动。将原始数据传入Matlab的kurtosis()函数可直接求得每个光纤的位置探测点所对应的峰度所组成的1×10 000矩阵。

现规定以40 个时间点位产生的数据为一组，如40×10 000的矩阵，即0.1 s 内10 000 个光纤位置采样点的所有数据。通过Matlab的max()和min()函数找出该子矩阵中每一列的最大值maxi和最小值mini，并将它们依次相减得到一组数据的包络，即规格为1×10 000的矩阵。利用循环结构多次执行相同的操作得到剩余9 组的包络数据，然后按行重新组合成为一个10×10 000的矩阵，该矩阵就是实验所取数据的包络矩阵。

2.2 TensorFlow实现数据的预处理

程序一般被分成两个部分，即构建阶段和执行阶段。在实验的构建阶段，大体定义了对原始数据的读取、滤波、求峰度和分段求包络这几个主要操作节点。由于TensorFlow 框架是针对深度学习推出的计算框架，对矩阵各种操作并不是很友好，因此为了利用其高效的运算效率，在整个过程中需要对矩阵的维度作各种变换以适应其运算格式。读取原始数据和定义各种常量以及转换数据为符合要求的格式后，首先创建一个实际将要在计算图中运行的输入数据变量data_input_original，并利用占位符tf.placeholder()创建该变量，在创建图的过程中并没有任何数值，只是使用占位符placeholder 来分配内存，最后在运行会话时再传入data_input_original 具体的值。此时定义的输入数据变量为500×10 000的矩阵，与上述Matlab 程序相对应。

在定义卷积滤波的操作节点中，首先定义滤波后的数据data_fli_0，然后使用tf.nn.conv2d(data_input_original,Num) 实现卷积操作，其中data_input_original 为输入数据变量，Num 为滤波器的卷积核，是一个54×1的矩阵组成的滤波器系数。

在计算峰度时，TensorFlow 库并没有自带的相关函数可以使用，因此需要根据公式实现。首先定义输入数据data_tt，为原始数据转置后的10 000×500 矩阵，利用自带的tf.div()和tf.reduce_sum()函数求得原始data_tt 每一行的均值，得到的kur_mean 是一个10 000×1的矩阵。再利用tf.tile()函数实现对kur_mean的扩充，以kur_mean 为整体，复制500 列得到一个10 000×500的矩阵kur_mean_tt。然后将原始数据矩阵 data_tt 和 kur_mean_tt 作差得kur_mean_sub。使用tf.square()函数对其平方计算得到kur_mean_sub2，再次平方得到kur _mean_sub4。分别对以上两个矩阵按行取均值，得到两个10 000×1的矩阵，即kur_ mean_sub2_m 和kur_mean_sub4_m，对kur_mean_sub2_m 平方得到kur_mean_sub2_m2，最后使用 kur_mean_sub4_m 除以kur_mean_sub2_m2 即可得到关于10 000 个位置探测点的10 000×1 峰度矩阵kur_cal。

在使用TensorFlow 框架计算包络时，依旧采用分段的方法，首先把原始数据利用tf.gather()函数按行进行切片，生成子矩阵，接着利用tf.transpose()函数将子矩阵进行转置，再分别使用tf.reduce_max()和tf.reduce_max()函数找出每一行的最值组成的两个10 000×1 矩阵，最后使用tf.subtract()将最大值矩阵和最小值矩阵相减得到一组包络。使用相同的操作得出剩余子矩阵的包络，最后利用tf.reshape()函数将这些子矩阵整合成10×10 000的矩阵。

在运行会话阶段，分别将读取的数据代入到已经创建的图中的各个变量与运算当中，同时将图中的各种操作保存到pb 模型文件当中。

3 NPU设备计算效果测试

华为NPU 设备作为外接移动运算设备，并不能直接使用TensorFlow 已经构建好的计算图并完成相应的计算，需要利用该平台所使用的MindStudio 开发工具，它运行在主机Linux 系统上。在运行模型文件前，需要将TensorFlow 生成的pb 文件通过开发工具MindStudio 按照相关参数转化为NPU 设备独有的离线om 模型，再将生成的离线om 模型和原始数据文件传到NPU 设备上，在主机端发送运行命令之后才能在NPU设备上调用om 模型来对原始数据文件进行预处理。NPU 设备将计算后的数据重新传入主机端，在主机端可以查看运算后的数据并作出相应的图形。

由于原始数据过于庞大，预处理后得到的包络和峰度只是两个矩阵，无法直观地展示测试效果，所以从数据中选取一部分来说明情况。相同的数据在不同设备上的预处理结果如表1 所示，CPU 端和NPU 端基本一致，造成该结果的原因在于程序对变量的计算和类型转换过程中出现精度丢失。峰度图如图4 所示，可以看出，在第七个位置探测点处峰度值约为9，大于报警阈值7，说明该处发生了振动。该探测点的包络数据图如图5 所示。

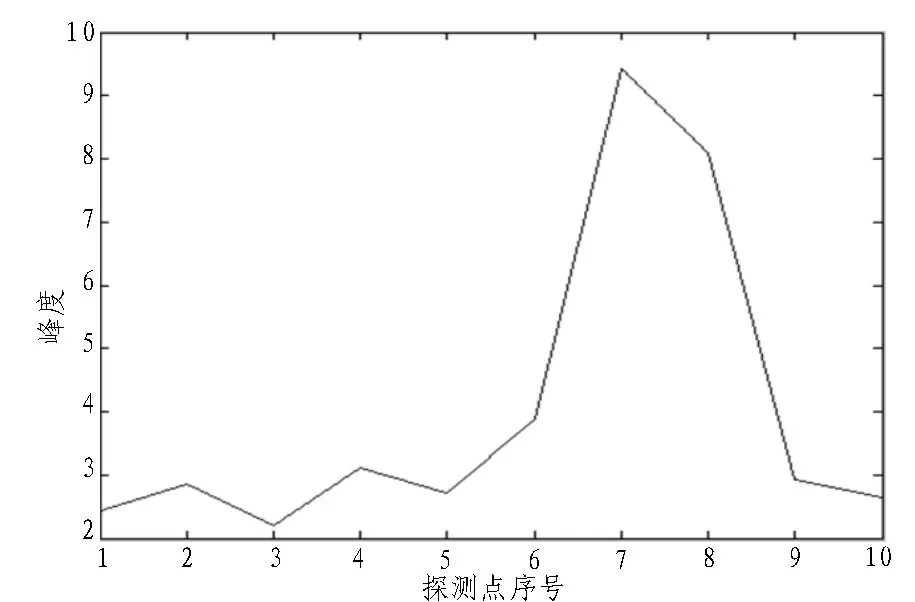
图4 峰度图

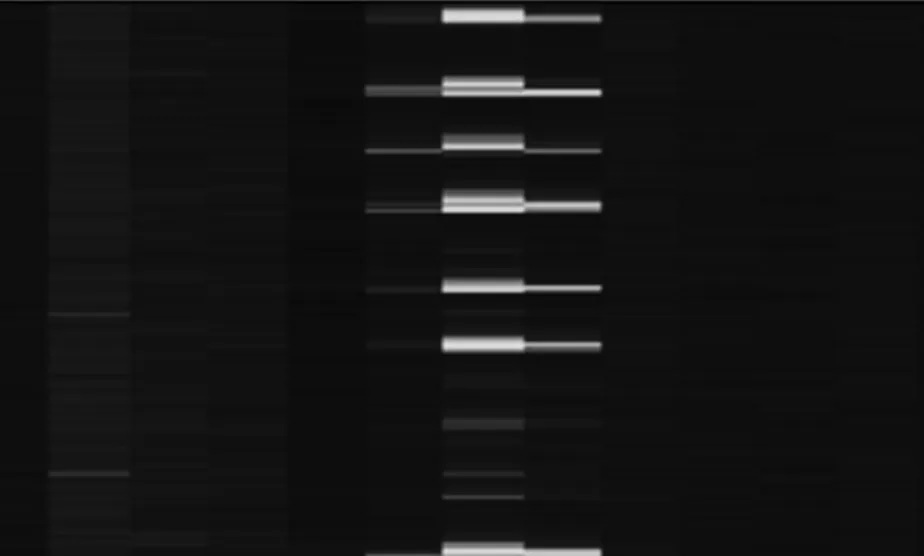
图5 包络数据图

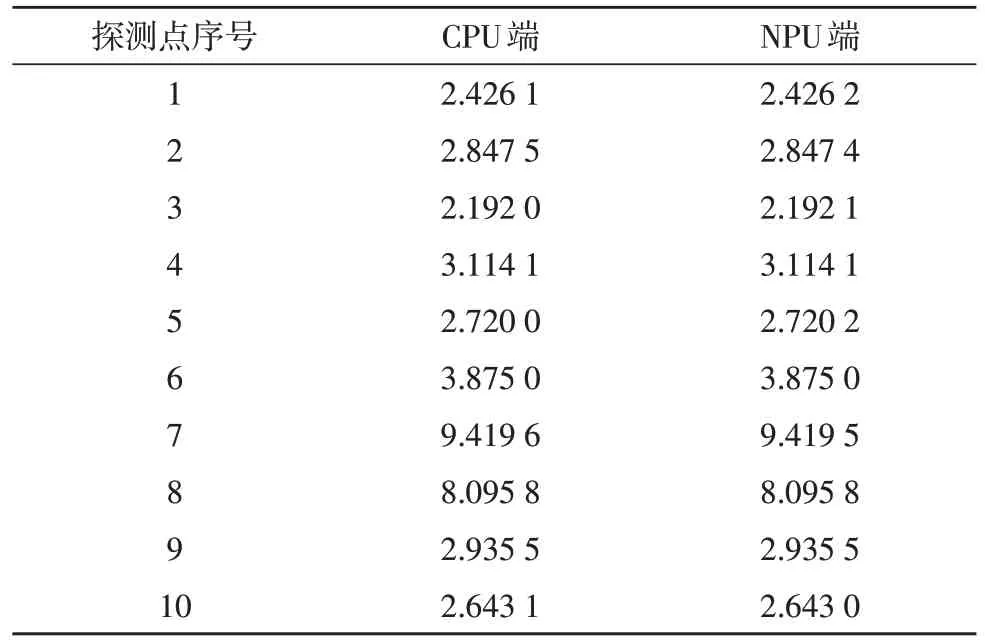
表1 不同设备峰度处理结果

在相同条件下选取规模相同的不同原始数据，利用计时函数分别多次计算CPU 端和NPU 端的计算时间，具体时间如表2 所示。

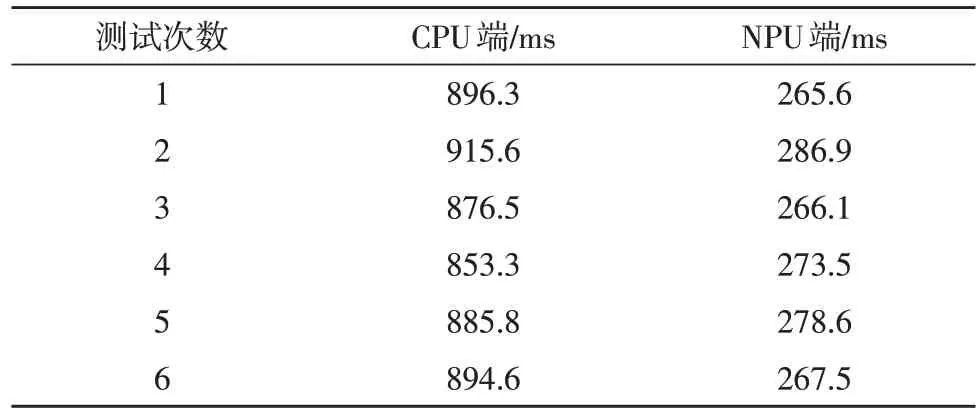
表2 在不同设备上进行预处理的计算时间

4 结论

针对传统的在CPU 端对光纤振动信号数据预处理中，处理速度慢、效率低的问题，文中提出并实现了基于TensorFlow 框架在NPU 设备上的光纤振动信号数据预处理的解决方案。实验结果证明，在CPU端的计算结果与在NPU 设备上调用om 模型得到的峰度和包络的计算结果基本一致，满足后续对振动模式识别所需的特征量的处理要求。多次取得不同段落的相同规模的原始数据计算包络和峰度所需时间约为280 ms，与原系统所用的900 ms 相比，效率约提升了3 倍，远远小于系统所需的1 s。但单纯比较NPU 与CPU的计算性能不可取，也不科学，考虑到实验所用的是本地数据，在实时检测中应综合考虑数据的传输开销和设备初始化所需的时间，数据的处理速度会有所降低。