基于支持向量机的变电站工程数据预测方法研究

薛礼月，刘鑫，黄亦章，阚竟生

（国网上海市电力公司经济技术研究院，上海 200002）

随着电网输变电工程尤其是变电工程的建设标准和数量不断提升，对其建设过程数字化程度的要求也越来越高[1-3]。基于人工智能算法的变电站工程造价计算，已经成为电网工程技术经济测算的辅助手段之一[4-6]。传统的计算造价方式为：电气专业向技经专业人员提供材料清册，技经人员手动录入物资并套取相应定额，工作量较大。通过利用电气三维设计模型，结合人工智能数据挖掘算法，能够有效减少识别录入资源的工作量。并将设备及材料实体清楚地展现、量化，能够有效提升三维设计造价的工作效率和准确性[7-10]。

基于统计学的变电站工程数据预测方法通常需要大量的历史数据用来训练，才可以得出相对准确的结果[11]。但考虑到不同电网工程项目存在不确定性，其所处位置、施工条件、设计技术要求等差异较大。单纯根据历史造价数据进行预测的准确度较低，易受高海拔、极端气候条件或其他因素的影响造成变电站工程造价较高[12]。

文中基于三维Revit 软件平台的变电站工程相关数据，以电压等级为分界，通过粒子群算法优化支持向量机（Support Vector Machine，SVM）的输入权重和隐层阈值[13]，对变电站工程造价数据进行分析并产生结果。最终通过将预测结果与变电站工程概算对比，验证了文中方法在辅助变电站工程造价测算方面的有效性。

1 变电站三维算量

1.1 三维造价

三维造价是提升变电站工程技经工作质量的重要举措。其能够实现自动化的造价编制，有助于提升工程造价中工程量计算的准确性以及工程计价的统一正确性。三维造价编制过程中能够形成结构化的工程造价数据，可以进一步辅助造价评审工作。同时基于Revit的变电站工程三维造价研究是建设“数字上海”的环节之一，是构建全业务数据链的重要环节，符合工程设计数据信息“一次录入、共享共用”思路。依托Revit 实现设计、技经阶段数据协同共享，有助于提高公司信息化水平[14]。

1.2 三维造价辅助测算

变电站工程的造价计算通常需要在前期洽谈阶段为业主提供一个初步的估算，且单一的造价计算手段较为繁琐，可能会出现较大的差异或错误。三维造价辅助测算可作为传统三维造价算量的参考和校对，避免由于软件BUG 或人为疏忽造成的缺量、材料冗余等问题[15-16]。

2 粒子群算法

2.1 数据预处理

变电站工程数据由于所处环境不同，造价差异较大，有时甚至不在一个数量级，可能存在或大或小的误差。因此，对变电站工程数据的预处理尤为重要[17]。

假设{Xt}是变电站工程各项设备数据异常的时间序列，则{Xt}利用ARIMA 模型的表示如下：

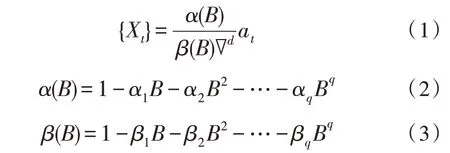
式中，α(B)是光滑算子，β(B)是可逆算子，∇是α1,α2,…,αq的缩写，B为延迟算子，α1,α2,…,αq代表α(B)的相应参数，β1,β2,…,βq代表β(B)的相应参数，是满足正态分布的噪音序列。变电站工程数据的异常类型通常为独立异常值模型。

2.2 算法改进

粒子群算法是一种仿生优化算法，其主要原理可用鸟群觅食行为阐述，对应关系如图1 所示。

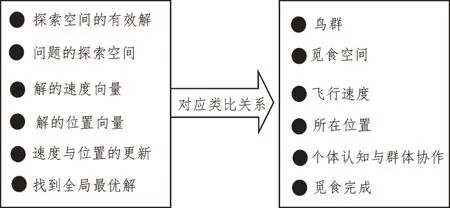
图1 粒子群算法与鸟群觅食行为对应关系

粒子用i表示，其速度和位置更新方程如下：

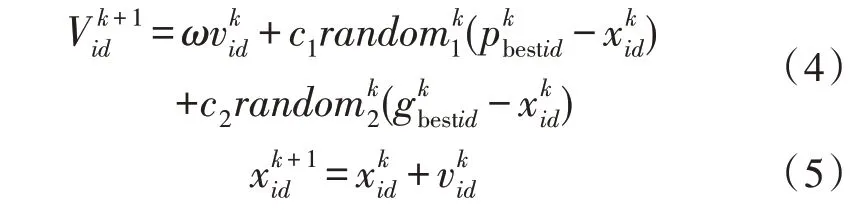
其中，ω为惯性权重，c1、c2为加速系数，其取值区间为[0，2]。random为随机数，取值区间为[0，1]。

为避免最优解的出现，各粒子的权重系数用αi表示，i=1,2,3,…,m，j=1,2,…,n，则：

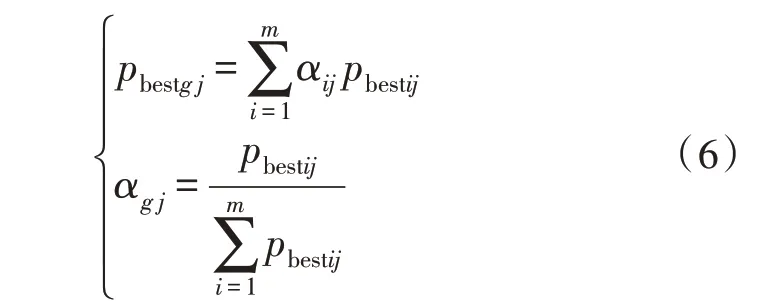
文中通过计算各个粒子的适应值和权重系数，使全局粒子均能得到兼顾，保证全局寻优的能力。

3 SVM及其改进措施

3.1 支持向量机

支持向量机以风险最小化为目标和原则，对样本数量要求较低，可在小样本情况下得到相对较准确的结果。

文中利用支持向量机算法进行预测，以变电站工程的历史需求数据作为输入；以各项子工程数据为输出结果。

3.2 隐藏层激活函数的选择

支持向量机的分类精准度仍受隐藏层激活函数g(x)的影响，激活函数主要包括二值激活函数、线性激活函数、Sigmoid 函数（也称为S 型激活函数）及径向基函数，常用的激活函数如下：

1）二值激活函数。其是指通过某种变化将样本数据二值化的一种函数，其表达式如下：

其中，U(xi)为阶跃函数。

2）线性激活函数：

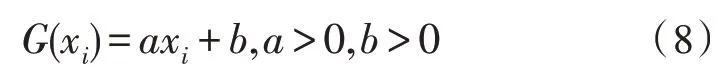
3）Sigmoid 函数：

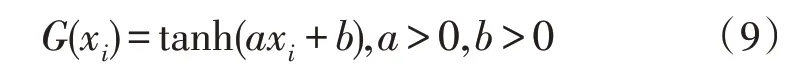
4）径向基函数：

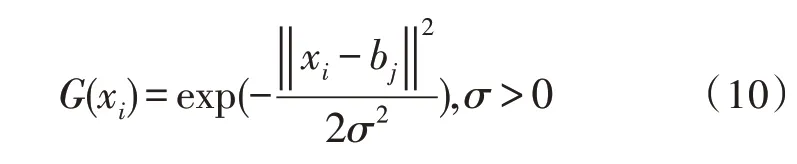
3.3 基于PSO优化的支持向量机

结合粒子群智能优化算法，对极限学习机的两个参数进行最优选择。

支持向量机输入层的功能是将接收到的模型之外的传入变量转到隐含层中；隐含层作为输入层与输出层之间的桥梁，不直接承担输入与输出的任务，其作用是对输入的数据进行计算、分类、识别等；输出层则是用于输出结果的一个工作阶段。总体算法原理如图2 所示。

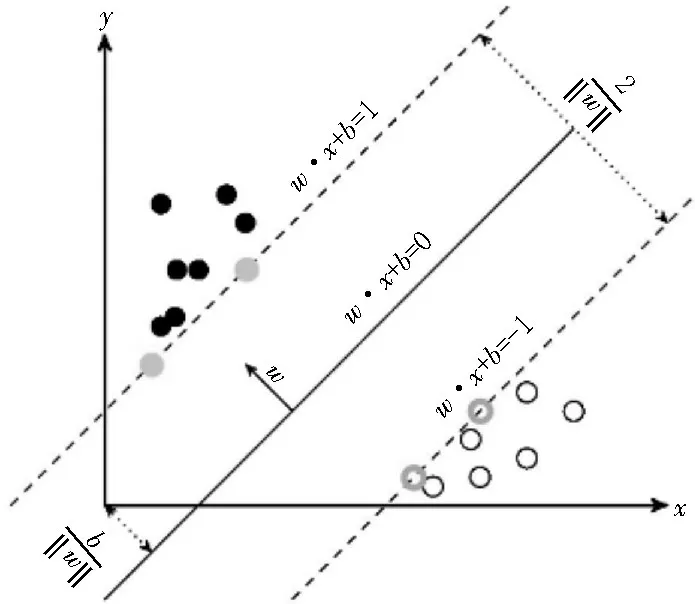
图2 支持向量机算法原理

假设输入层与隐含层之间的连接权值矩阵为w，则w如下式：

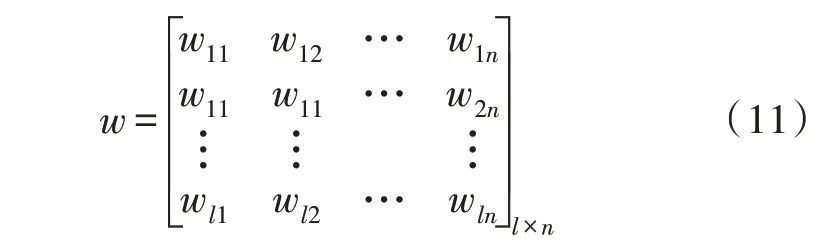
w的含义是输入层与隐含层之间的连接函数，通常称为输入权值函数。

初始化单个个体初始值如下式：

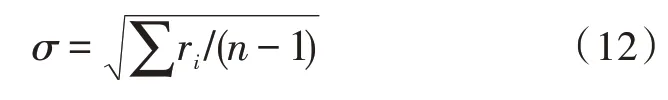
其中，r为一组测量值与期望值间的偏差，每次迭代中首先比较测量值Fi与期望值pbest的数值。若Fi＜pbest，则由Fi代替pbest成为最新的pbest；否则，维持现状。然后比较Fi与gbest的数值，若Fi＜gbest，则Fi取代gbest作为当次的最优解；否则，维持gbest取值不变。

4 主要流程

以变电站工程历史数据为基础样本，按变电站的电压等级进行区分。为保持辅助预测的统一性，样本均采用双主变且容量相等的工程，流程如图3所示。

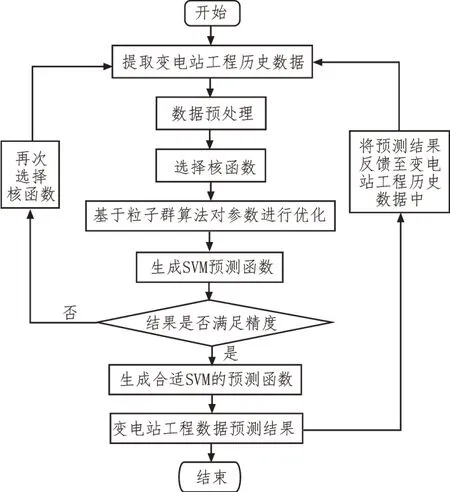
图3 基于SVM的变电站工程预测主要流程

具体步骤如下：

1）收集提取35 kV、110 kV 及220 kV 变电站工程的历史数据，主要是变电站的各分项工程造价；

2）根据2.1 节所述内容进行数据预处理，剔除掉异常数据或错误数据；

3）选择合适的核函数，文中所述方法采用混合核函数；

4）基于粒子群算法对支持向量机的输出权值和隐层阈值等相关参数进行优化；

5）根据步骤4）所得结果，训练生成SVM 预测函数，并输入样本进行测试。然后判断所得结果的精度是否满足要求：若满足，则输出该预测函数；若不满足，则再次选择核函数，重复步骤1）～4）；

6）输出预测结果。

5 算例分析

文中通过收集各个电压等级的数据样本，以变电站工程项目所在的电压等级、海拔高度、地质条件（A、B、C）等作为输入。结合第4 节的步骤产生预测函数，并将输出结果与各个电压等级工程的数据信息平均值进行对比，以此凸显文中通过改进支持向量机的预测模型的有效性。

5.1 激活函数选择

为了选出最合适的隐藏层激活函数，实现最高的诊断准确率，文中采取试探对比的方法进行。选取233 组样本进行对比，其中150 组作为训练样本，另外73 组作为测试样本。保持隐藏层神经元个数相同，均为32 个。对激活函数进行性能对比，仿真结果如表1 所示。

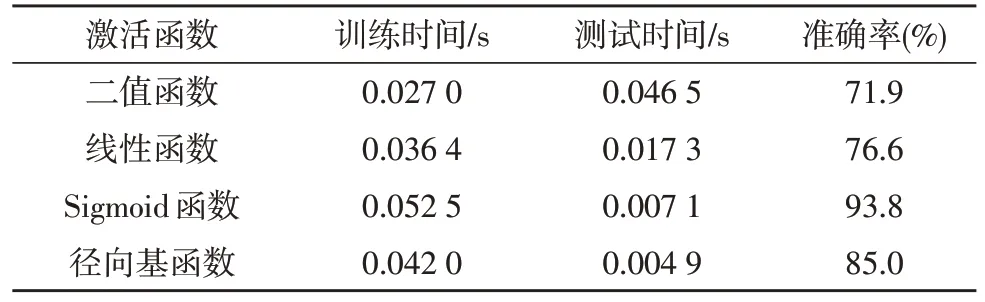
表1 激活函数性能对比

文中选择Sigmoid 函数和径向基函数的混合作为激活函数。

5.2 隐藏层节点

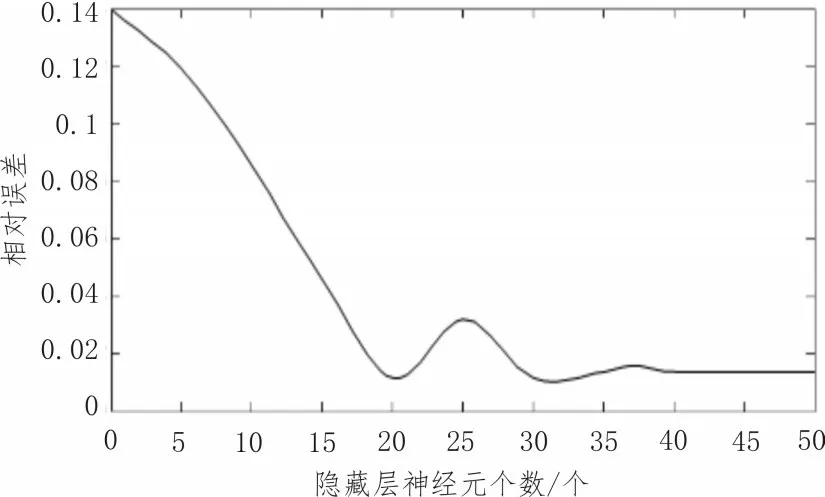
图4 神经元个数与分类精度的关系曲线

5.3 结果对比

为了验证文中所提方法的有效性和正确性，将SVM 预测方法与各个电压等级平均值比较，结果对比如表2 所示。在35 kV 电压等级，由于变电站工程数据相对较小、各种费用相对较低，其平均值和文中SVM 预测值准确度差异较小。但随着电压等级的提升，110 kV 和220 kV 电压等级的准确度差别逐渐增大，表明了文中算法的有效性，能够在变电站工程开展的前期阶段预测各项工程数据，为变电站工程项目的决策提供参考。

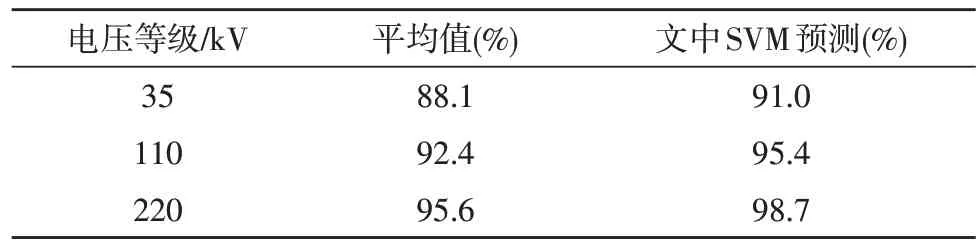
表2 计算结果对比

6 结束语

文中将变电站工程中的历史数据作为数据来源，基于数据挖掘技术，采用粒子群算法设计改进的支持向量机，优化支持向量机算法的拓扑结构、激活函数、隐层阈值和输出权值，并取得了较好的效果，能够在变电站工程开始的前期准备阶段迅速得出相对准确的变电站工程数据预测结果，模型计算结果验证了文中方法的有效性。但考虑到变电站工程所处环境的复杂性，同时随着数据挖掘计算的不断进步，这类预测算法仍有进一步优化的潜力，例如：1）根据变电站所处地理环境进一步增加输入历史数据的维度，将能够更加准确地预估变电站的各项数据；2）时刻跟踪新型人工智能数据挖掘算法，提升变电站工程数据预测的准确性与效率。