基于DTS的多模态异构大数据检测方法研究

肖楠

（西安交通工程学院公共课部，陕西西安 710300）

大数据检测是一种相对有效的机器学习型信息处理手段，可在已知数据存储行为的基础上，将信息参量整合成全新的应用传输形式[1-2]。传统的数据检测手段可在局部离群因子的作用下，确定局部异常点所处的实际位置，再通过信息复杂度对比的方式，实现对异构型数据参量的反馈与对比[3]，如基于两级分段模型的异构数据处理与检测方法[4]，但此方法并不能完全规避大数据网络中的风险性信息传输行为，易导致数据稳定抵抗能力的持续下降。

数据转换服务（Data Transformation Service，DTS）特指DTS 解码原理，可以直接对数字信号源进行分类处理，然后再按照既定顺序将信息参量发送至核心应用主机之中。与其他数据处理手段相比，DTS 解码可在无接入设备作用的前提下，将原始信息参量直接转存至数据库结构体中，再借助输入、输出信道，将这些文件参量转换成其他存储形式，从而满足与多模态异构数据相关的检测处理需求[5-6]。

因此，针对传统方法存在的不足，提出基于DTS的多模态异构大数据检测方法，在深度置信网络的基础上，建立必要的线性映射条件，再通过数据参量清洗的方式，实现对异构数据的降维处理。

1 多模态异构大数据提取

基于DTS的多模态异构大数据提取由深度置信网络搭建、异构数据编码、DTS 线性映射条件设置3 个环节共同组成。

1.1 深度置信网络

深度置信网络结构如图1 所示。

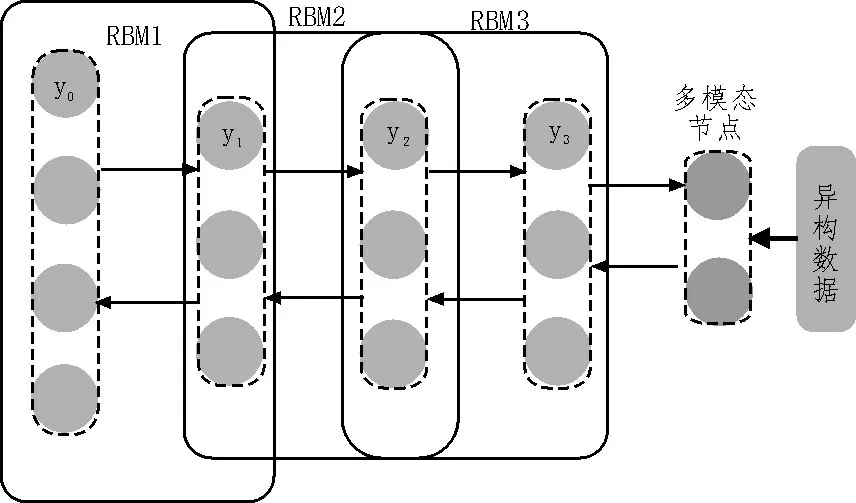
图1 深度置信网络结构图

深度置信网络由RBM1、RBM2、RBM3 3 个模块单元结构共同组成。其中，RBM1 单元负载一列y0节点和一列y1节点，前者能够判断DTS 环境下，多模态异构大数据是否具备继续传输的能力，后者可根据既定检测指令的传输行为，将已打包的信息参量由顶层异构结构体反馈至底层异构结构体之中[7-8]。RBM2 单元负载一列y1节点和一列y2节点，两者互相联合，形成完整的异构型大数据传输单元，并可在DTS 解码原理的作用下，实现对信息参量的整合与处理。RBM3 单元位于深度置信网络底层，可在多模态节点的作用下，将散乱分布的大数据信息整合成异构型传输形式。

1.2 异构数据编码

异构数据编码可在深度置信网络的基础上，对DTS 型信息参量进行初步的整合处理，一般情况下，需要原编码节点、过度法则、多模态结构体三类执行结构的共同配合[9]。原编码节点同时存在于深度置信网络的两端，可在过度法则的作用下，变更多模态异构体的现有连接形式，并可遵照DTS 信道传输行为，将这些信息参量反馈至核心数据库存储单元之中。过度法则对异构数据编码原则进行了集中化约束，可在联合原编码节点与多模态异构体的同时，感知DTS 环境中大数据信息参量的现有传输形态，并可按照信息检测机制的作用形式，对各项大数据结构体进行集中化处理[10]。

异构数据编码原理如图2 所示。

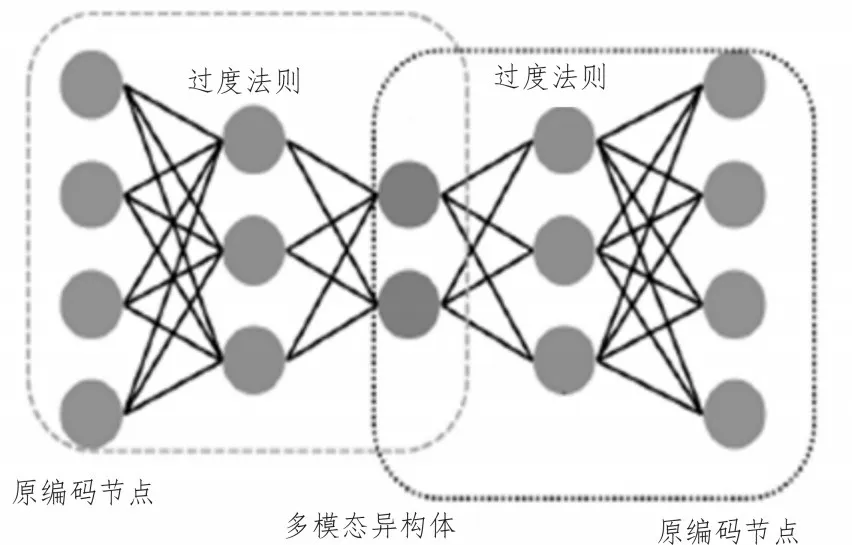
图2 异构数据编码原理

1.3 DTS线性映射条件

DTS 线性映射条件是与多模态异构大数据相关的信息检索标准，可在已知数据存储权限值的基础上，对待检测信息存储形式进行重新安排，从而实现对大数据异构模态行为的规划与协调。数据存储权限值可表示为λ，在既定检测时长内，该项物理量的实值水平越高，多模态异构大数据的待处置应用量也就越大。xn代表最后一个输入的大数据异构体参量，n代表与该指标匹配的多模态系数指标。x1代表第一个输入的大数据异构体参量，联立上述物理量，可将大数据网络中的DTS 线性映射条件定义为：

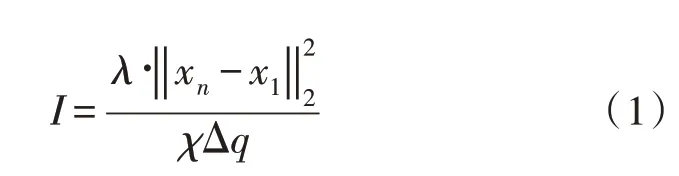
其中，χ代表DTS 环境下与多模态大数据相关的异构处理应用量，Δq代表单位检测时长内大数据检测行为指标的实际变化量。

2 多模态异构大数据检测方法

在DTS 提取原理的支持下，按照数据参量清洗、二值化转换、异构数据降维的处理流程，实现新型多模态异构大数据检测方法的顺利应用。

2.1 数据参量清洗

数据参量清洗流程如图3 所示。

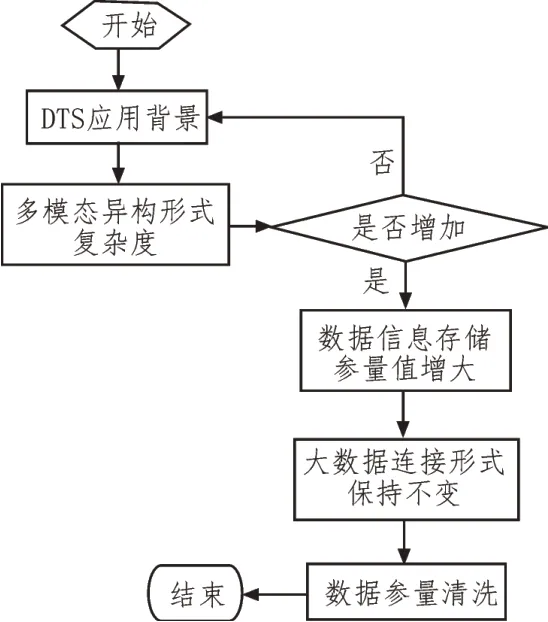
图3 数据参量清洗流程图

数据参量清洗是与多模态异构大数据检测相关的重要信息处理流程，常以获取DTS应用背景作为起始执行环节。一般情况下，随着信息多模态异构形式复杂度的增加，数据信息的存储参量值也会随之增大，直至将检测数据库的存储空间完全填满11-12]。若多模态异构大数据的连接形式始终保持不变，最终信息检测结果的有效性只与参量之间的编码原则相关，且在DTS 线性映射条件的作用下，待处理的大数据总量越多，最终所获得的参量清洗结果也就越明显，反之则难以获取到理想化的信息检测结果[13-14]。

2.2 二值化转换

二值化转换是一种有效的多模态异构信息处理行为，可在大数据网络中联合所有待编码的DTS 节点，一方面降低异构数据之间的关联度水平，另一方面缩短信息与信息之间的实际传输距离[15-16]。在不考虑其他干扰条件的情况下，二值化转换结果只受数据参量清洗基向量、数据存储方向权值两项物理量的直接影响。

将数据参量清洗基向量表示为αn，在既定检测条件下，随着已输入信息数量级水平的提升，该项物理指标的实际数值等级也会随之增大。数据存储方向权值可表示为Kˉ，一般情况下，若该项指标的表现实值不超过自然数1，则可认为最终的检测执行结果可取。联立式（1），可将多模态异构大数据的二值化转换结果表示为：

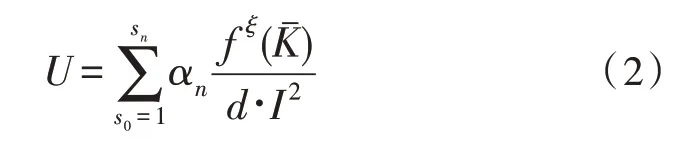
其中，s0代表最小的信息多模态异构系数，sn代表最大的信息多模态异构系数，f代表两个相邻大数据信息参量间的实际传输距离值，ξ代表幂次项应用指标，d代表常性转换系数。

2.3 异构数据降维

异构数据降维是多模态异构大数据检测方法应用的末尾处理环节，可在DTS 环境中，根据二值化转换原理的作用权限，确定数据信息在单位时间内的实际存储数量值。规定ΔT代表一个单位检测时长，随着多模态异构信息输入量的增加，与之相关的检测时间消耗实值也会逐渐增大，直接与大数据应用主机的处置权限完全相符。设L～ 代表符合DTS 环境存储标准的数据消耗权限值，一般情况下，如果不出现明显的差异化数据异构行为，该项物理量的实际数值水平也不会出现明显的变化状态。在上述物理量的支持下，联立式（2），可将多模态异构大数据的降维处理结果表示为：

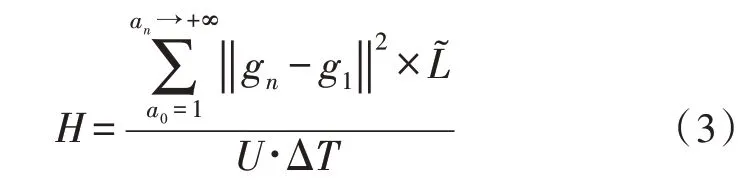
其中，a0代表与多模态大数据参量相关的最小连接异构条件，an代表多模态大数据参量相关的最大连接异构条件，gn、g1分别代表两个非同时输入的待检测信息参量指标。至此，实现各项参量系数指标的计算与处理，在DTS 解码原理的支持下，完成新型多模态异构大数据检测方法的搭建。

3 实用能力检测

为验证基于DTS 多模态异构大数据检测方法的实际应用价值，设计如下对比实验。

在大数据网络中，截取两组等长的传输数据参量，分别作为实验组、对照组检测处理对象。令实验组执行主机搭载基于DTS 多模态异构大数据检测方法，对照组执行主机搭载传统的基于两级分段模型的异构数据处理与检测方法，在确保其他干扰条件保持不变的情况下，记录各项实验指标的实际变化情况。

出于实验公平性考虑，除所用检测方法不同外，实验组、对照组所有应用指标全部保持一致。实验参数设置情况如表1 所示。

表1 实验参数设置

IID 指标能够反映与检测主机匹配的信息传输行为风险性规避能力，一般情况下，指标数值越大，检测主机所具有的规避能力也就越强，反之则越弱。表2 记录了实验组、对照组IID 指标的具体变化情况。

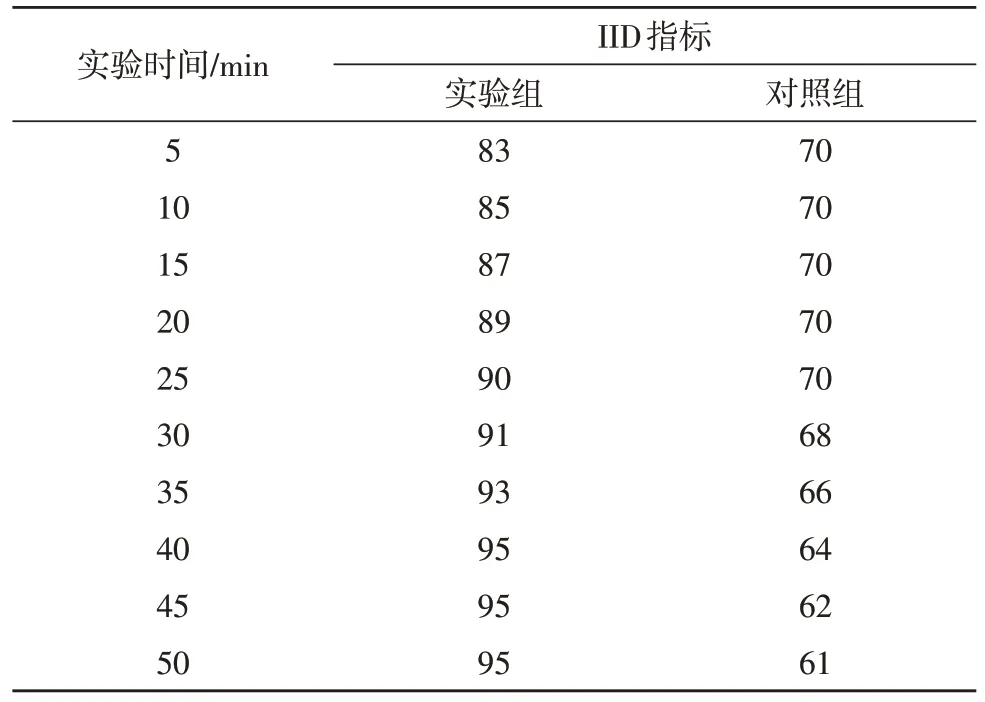
表2 IID指标对比表

分析表2 可知，随着实验时间的延长，实验组IID 指标始终保持先上升、再稳定的变化趋势，全局最大值能够达到95%，且能够出现10 min的数值稳定状态。对照组IID 指标则在20 min的稳定状态后，开始不断下降，全局最大值仅能达到70%，与实验组极值相比，下降了25%。综上可知，应用基于DTS 多模态异构大数据检测方法，可大幅提升IID 指标的数值水平，从而增强与检测主机匹配的信息传输行为风险性规避能力。

PEI 指标能够反映多模态异构数据的稳定抵抗能力，一般情况下，前者的数值指标越大，后者的稳定抵抗能力也就越强，反之则越弱。表3 记录了实验组、对照组PEI 指标的实际数值变化情况。

分析表3 可知，随着实验时间的延长，实验组PEI 指标始终保持上升、下降交替出现的变化趋势，全局最大值能够达到82%。对照组PEI 指标则保持先上升，再稳定，最后下降的变化趋势，全局最大值仅能达到56%，与实验组极值相比，下降了26%。综上可知，应用基于DTS 多模态异构大数据检测方法，可使PEI 指标数值得到有效提高，满足增强多模态异构数据稳定抵抗能力的实际应用需求。

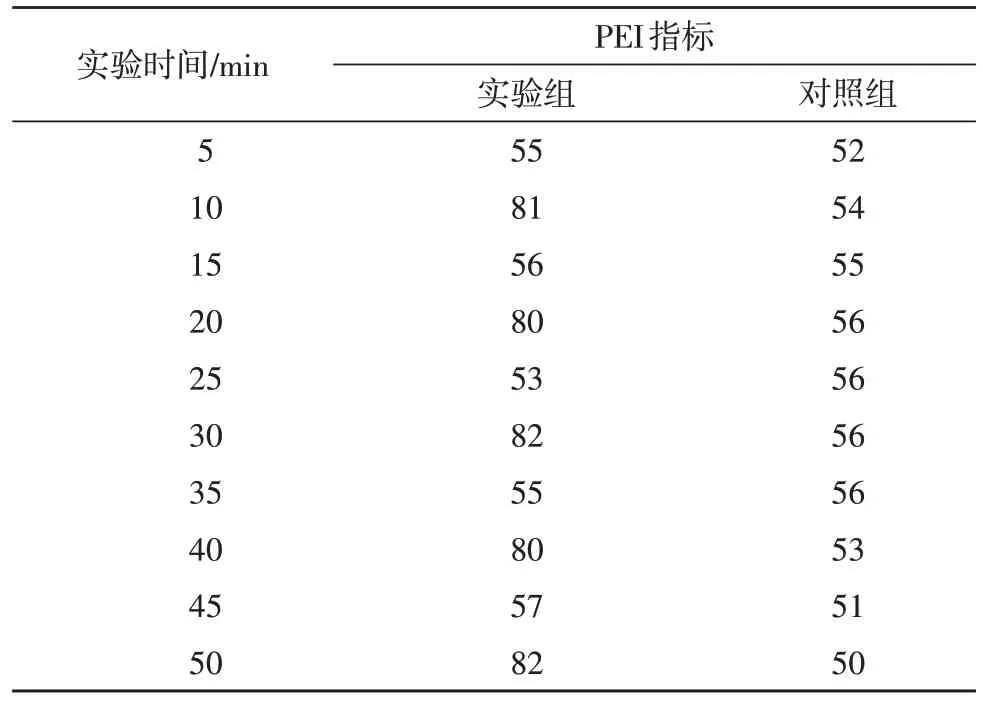
表3 PEI指标对比表

4 结束语

与传统的异构数据检测手段相比，新型多模态异构大数据检测方法可在DTS 编码原理的作用下建立必备的线性映射条件，也可在联合深度置信网络的同时，确定与异构数据相关的实际编码原则。若能够保障数据参量的清洗能力，则能够在二值化转换技术的作用下，实现对异构数据的降维处理。从实用性角度来看，IID 指标与PEI 指标数值的提升，能够大幅加强与检测主机匹配的信息传输行为风险性规避能力，且可实现对多模态异构数据稳定抵抗能力的有效保障。