基于粒子群算法的中低压配电网无功补偿协同优化方法

林巧红，翁知颖，张国星

（国网浙江丽水市莲都区供电有限公司，浙江丽水 323000）

粒子群算法也叫微粒群算法、粒子群优化算法或微粒群优化算法，以模拟鸟群觅食行为作为基本应用原理，是一种基于群体协作的随机性搜索算法[1]。通常情况下，在实际应用过程中，该算法的所有数值解都保持随机分布的排列形式，通过多次信息迭代处理，找寻其中隐藏的最优解。每一次迭代过程中，一个最优数值可通过跟踪两个相关“极值”的方式，实现对自身所属信息数据的更新[2-3]。在中低压配电网环境中，单波电子补偿控制模型可直接记录耗电容易的投切组数，并可以根据传输电子之间的负荷聚合作用，确定与之相关的电量协同调度策略[4]。

然而，此方法很难保障电子传输流失效率始终保持在较低应用水平，基于此，引入粒子群算法，设计一种新型的中低压配电网无功补偿协同优化方法，并通过对比实验的方式，突出两种补偿调试策略之间的实用差异性。

1 配电网模糊性规划

配电网模糊性规划包含电压偏移量计算、中低压配电约束条件确定、目标模糊函数建立3 个处理流程。

1.1 电压偏移量

电压偏移是一种电子转移行为，在中低压配电网环境中，实际应用电子总量不断增大，待处理的电子连接轨迹也会随之不断延长，直至处于最末端位置的应用电子与处于初始位置的应用电子完全重合[5]。在粒子群算法中，所有传输电子可被认为是一个独立的数值解，而最终偏移量结果的筛查，则在多重处置原则的支持下，借助电压与电流之间的数值限定关系，确定实际电压量的实际数值偏差结果。

设U代表实际运行环境下中低场电压均值，在不考虑其他外界干扰的情况下，该项物理值具备较强的应用稳定性。I代表配电网环境中的直行电流均值，与应用电压相比，该项物理量的可变性较强，但由于电流值始终属于跟随性变量，故其实值范围依然受到不同电网设备的电阻数值影响，可将基于粒子群算法的电压偏移量表示为：

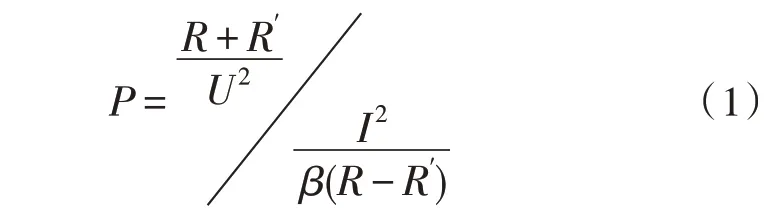
式中，R代表核心电阻数值，R′代表既定电网设备的电阻数值，β代表电压量取值系数。

1.2 中低压配电约束条件

中低压配电约束条件包含上限影响参量和下限影响参量。上限影响参量也叫最高电压输出条件，常表示为χ↑，在一个电子传输周期内，该项物理量的实际表现状态基本呈现明显的两级分化状态，即电压偏移量越大，配电约束条件的上限影响参量值越大，反之则越小。下限影响参量也叫最低电压输出条件，常表示为χ↓，在一个电子传输周期内，该项物理量的实际表现状态始终受到上限变动参量的影响，即上限影响参量越大，下限影响参量越大，反之则越小。在上述物理量的支持下，联立式（1），可将基于粒子群算法的中低压配电约束条件表示为：

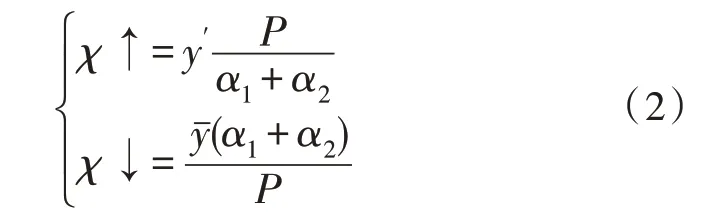
式中，α1、α2分别代表两个不同的电压应用系数，y′代表配电网电压的最大补偿系数，yˉ代表配电网电压的平均补偿系数。

1.3 目标模糊函数

目标模糊函数是与中低压配电约束条件直接相关的电子传输限定函数，在已知传输电子量数值的情况下，两个随机电压量之间的物理差值越大，模糊函数应用等级越高，反之则越低[6-7]。在不考虑其他干扰条件的情况下，目标模糊函数受到电压量最大值、电压量最小值两项物理量的直接影响[8]。其中，电压量最大值表示为q～，在固定电子传输周期内，该项物理量具备较强的应用稳定性，且随着传输电流总量的不断提升，该项物理系数也会产生明显的应用坡度极值。电压量最小值表示为q～，在固定电子传输周期内，该项物理量始终与电压量最大值保持相同的变化趋势，且随着传输电流总量的不断提升，该项物理系数虽会产生应用坡度极值，但平均变化幅度相对较小。在上述物理量的支持下，联立式（2），可将中低压配电网无功补偿的目标模糊函数定义为：

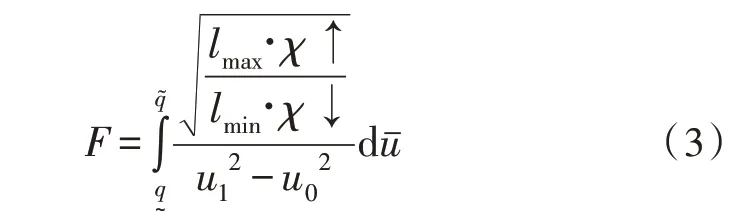
式中，lmax代表中低压环境下最大配电量数值，lmin代表中低压环境下最小配电量数值，u1、u0分别代表两个不同的粒子群应用系数，uˉ代表u1与u0的平均数值。

2 中低压配电网无功补偿的协同优化

在配电网模糊性规划的支持下，按照主要元件谐波域确定、无功谐波潮流计算、电子量协同优化配置的处理流程，完成中低压配电网无功补偿协同优化。

2.1 主要元件谐波域

在中低压配电网环境中，主要无功补偿元件的分布始终满足谐波域的划分原理。在粒子群算法作用下，整个公用配电网始终保持相对稳定的执行状态，随着公共补偿连接点被逐渐占用，所有配电网用户都能得到足量的传输电子，直至将所有极限电子参量完全串联在一起[9-10]。主要元件谐波域是一个呈发射状覆盖的物理电子区间，理论电子量从一个域节点传输至另一个域节点所需的应用时间是谐波电子覆盖整个配电网空间所需的物理时间[11]。

设k0代表电子传输域节点的起始位置，k1代表电子传输域节点的终止位置，联立式（3），可将中低压配电网环境中的主要元件谐波域计算式定义为：

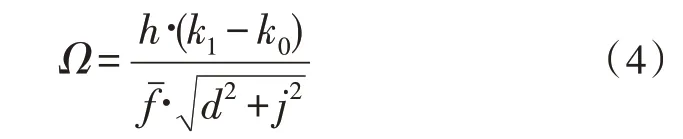
式中，h代表既定配电系数，d、j分别代表两个不同的电子谐波输出条件，fˉ代表中低压应用电子的协同传输均值。

2.2 无功谐波潮流

无功谐波潮流是中低压配电网协同优化处理的基础条件，可在主要元件谐波域空间的支持下，确定电子量在电网环境中的平均传输权限。造成无功谐波潮流情况的影响因素相对较多，且每种潮流主体所对应的电量负载类型也均不相同，为使电子潮流的非线性负载系数逐渐趋于稳定，在既定配网传输环境下，时刻监测谐波电子的平均分布情况[12-13]。

以最小电网无功差异量g0、最大电网无功差异量g1作为基础判别条件，在整个中低压配电网空间内，令Ω实值始终大于物理数值1，联立式（4），可将中低压配电网的无功谐波潮流表示为：

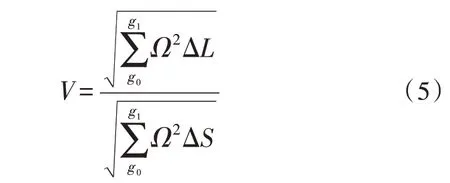
式中，ΔL代表电网粒子系数在单位时间内的实际变化量，ΔS代表协同优化系数在单位时间内的实际变化量。

2.3 电子量的协同优化配置

电子量协同优化配置是实现中低压配电网无功补偿协同优化方法应用的末尾处理环节，在粒子群算法的支持下，待传输的电子总量越大，产生的干预电压数值也就越高，物理传输电流不断增大，反之则引起物理传输电流的不断减小[14]。为使中低压配电网无功补偿机制得到完善，在电子量系数保持不变的情况下，协同优化配置处理手段将直接影响电子流量的实际输出数值，通常情况下，前者应用等级越高，后者数值水平越高，反之则越低[15-16]。

设c代表电网无功补偿量的平均作用边界条件，联立式（5），可将电子量的协同优化配置结果表示为：

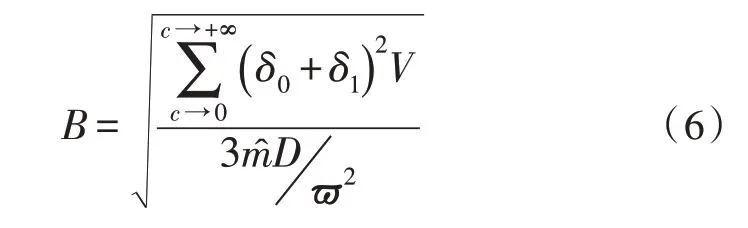
式中，δ0、δ1分别代表两个不同的配电传输应用条件，m^ 代表电子流量的无功配置系数，D代表中低压配网环境中的电量应用均值，ϖ代表定向化协同优化处置权限。至此，完成各项应用系数的计算与处理，在粒子群算法的支持下，完成中低压配电网无功补偿协同优化。

3 实验分析

为验证所提方法的实际应用价值，设计对比实验。将中低压配电网输出主机调试至最佳执行状态，在无功补偿型断路控制器的作用下，控制应用电子在电网环境中的基本传输环境，其中，实验组主机搭载新型协同优化方法，对照组主机搭载单波电子补偿控制模型，在相同实验环境下，记录各项实验指标，具体实验环境如图1 所示。

图1 实验环境

中压传输环境下电子传输流失效率的具体变化情况如表1 所示。

分析表1 可知，在中压传输环境下，实验组电子传输流失效率的变化趋势相对较为平缓，全局最大值24.7%与全局最小值23.2%之间的差值仅为1.5%。对照组电子传输流失效率始终保持不断上升的变化趋势，全局最大值达到48.7%，与实验组极值相比，上升了25.5%。综上可知，在中压传输环境下，应用新型配电网无功补偿协同优化方法，能够实现对电子传输流失效率的有效控制。

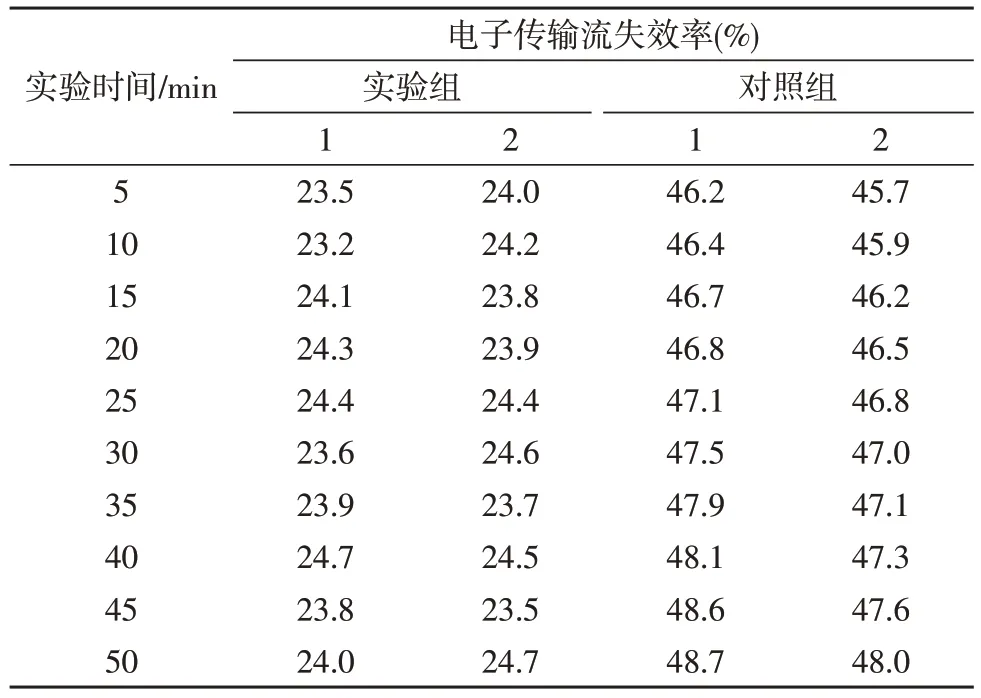
表1 中压传输环境下的电子传输流失效率

表2 反映低压传输环境下电子传输流失效率的具体变化情况。

分析表2 可知，在低压传输环境下，实验组电子传输流失效率保持先上升、再稳定的变化趋势，全局最大值可达到21.9%。对照组电子传输流失效率则基本保持阶梯状上升的变化趋势，全局最大值达到42.7%，与实验组极值相比上升了20.8%，验证了所提方法的有效性。

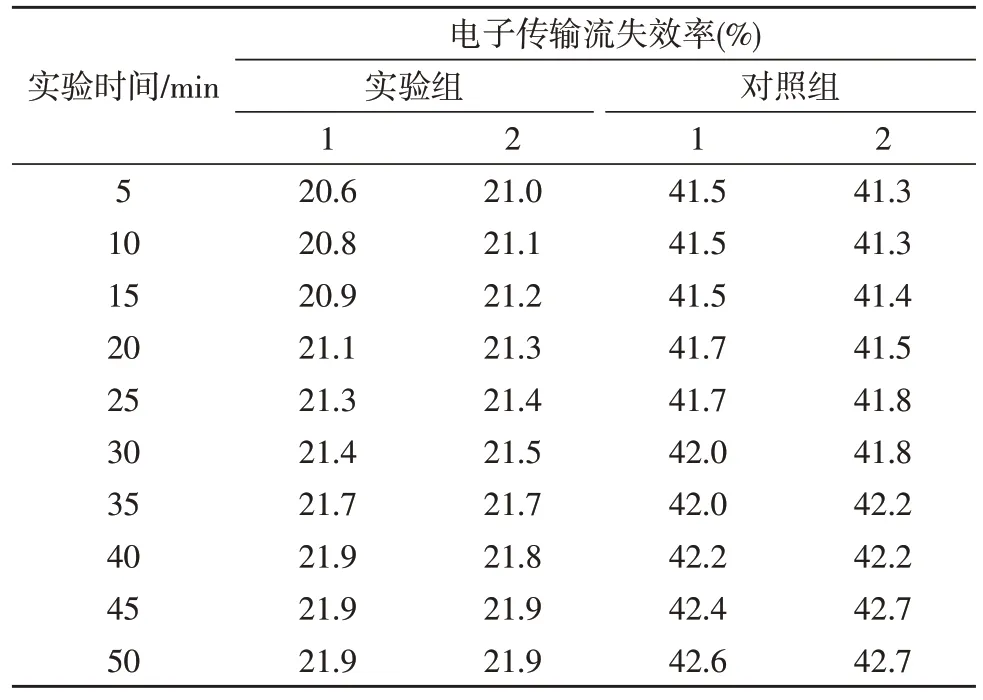
表2 低压传输环境下的电子传输流失效率

4 结束语

在粒子群算法的支持下，新型配电网无功补偿协同优化方法针对单波电子补偿控制模型电子传输流失效率过高的问题进行改进，在无功谐波潮流系数的作用下，实现对电子量与谐波域的同步调节。从实用性角度来看，中低压环境下的电子传输流失效率均得到了有效控制，满足集中性配电网优化调度的实际处理需求。