一种三维模型多层级视点描述符

曾 升,周蓬勃,周明全,

(1.西北大学 文化遗产数字化国家地方联合工程研究中心，陕西 西安 710127；2.西北大学 信息科学与技术学院,陕西 西安 710127;3.北京师范大学 教育部虚拟现实应用工程研究中心，北京 100875)

3D模型的数量增长十分迅速,从不同视角的2D图像中开发算法来识别3D模型十分流行。人类观察世界获取某一个视角的画面,再由多个角度的视图达到对物体的全面认识,从所有视角看到的三维模型是相似的,则三维模型是相似的思想广泛应用于计算机视觉领域。本文针对到底怎样的视角组合会更加有效地识别3D模型,提出多层级视点描述符识别三维模型,并为3D模型提供了一组最优的二维视图选择。

3D形状的识别经常使用三维模型全局[1-5]或局部特征描述符[6-10]，不同特征描述符的使用及算法的设计对三维重建、三维模型的检索等应用影响非常大,优异的特征描述符有益于推动计算机视觉应用的发展,比如,得益于SIFT[11]特征对3D视点各种变换都持一定程度的稳定性,能够从多张照片有效重建三维模型[12],也是3D模型检索的理想属性[13]。而深度学习能够更加“自动”地提取特征,在特征提取及实时运行方面都有着极大的优势,从而出现大量优秀的算法[14-19]。然而,并不意味着手工描述符就不再有用,在基于草图的三维模型检索中,手工设计的3D-SIFT[20]被用来提取3D模型部分的特征,草图部分用预训练的AlexNet提取特征,深度相关度量学习方法(deep correlated metric leaning,DCML)有效建立了易于人类理解的草图和三维模型这两种不同模式数据间的桥梁[21]。手工设计描述符对深度学习的设计与改进仍存在有益影响。本文提出的多层级视点描述符MLVD具有较强的区分能力,并且为3D模型提供一组最优视图,相当于同类的三维模型都会有一组相似的观察视点。图1是在密集的观测球上计算的一组最优视点,其中红色点是第2层级的视点，蓝色点是第3层级的视点。MLVD-3提供的一组视图组合在MVCNN的对比实验中,在精细分类的数据上的识别精度有非常明显的提升。

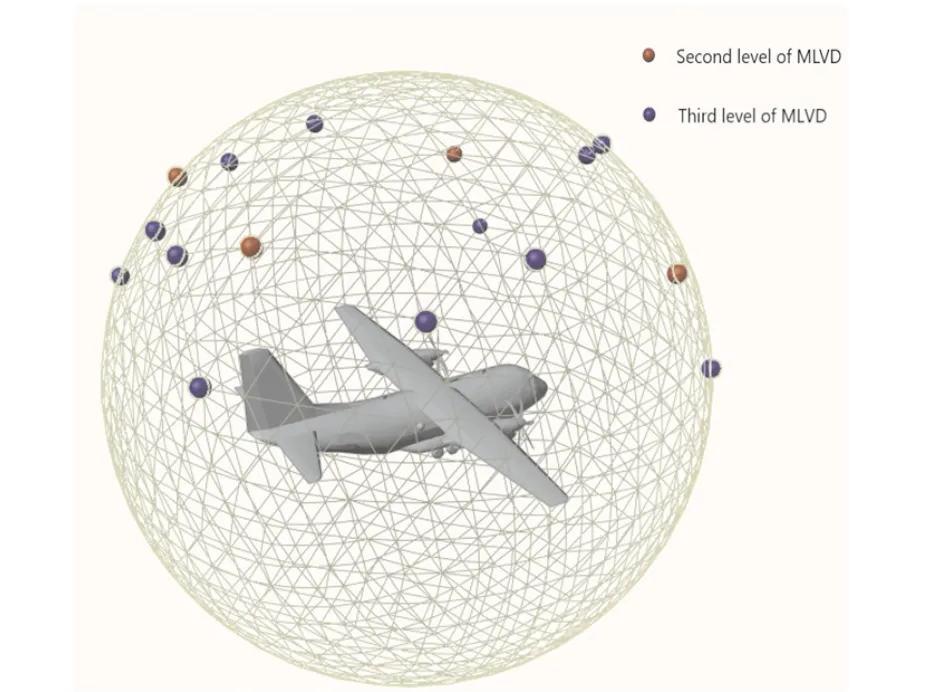
图1 第2和第3层级视点描述符Fig.1 The second and third level viewpoint descriptors

1 相关工作

多视图算法从不同角度的视觉信息来探索物体,把三维模型放在球体中,在不同的视点观察球体中心的三维模型会得到不同角度的视图,这种分析三维模型特征方式是通过模仿人类对象识别行为[22]。在光场描述符中(light field descriptor,LFD),光场相机放在正12面体的20个顶点上,而相对顶点投影轮廓相同,所以旋转模型进行采样前仅需要渲染1组半球上的10个不同轮廓,并计算轮廓的Z矩和傅里叶系数作为描述符[23]。还有一些算法先解决3D对象的归一化问题,再实现精确匹配,三维模型的归一化非常影响模型的匹配效率与准确度，而视图的选择仍然是均匀采样的,比如Chaouchy的研究中由正12面体顶点绘制的20幅深度图像来表示三维模型[24],而Lian的时钟匹配方法使用正8面体细分1次后的18个顶点获取深度图[25]。还有对旋转鲁棒的仰角描述符,获取前后上下左右6个不同视图的高程信息后,比较720次完成匹配[26]。

然而,存在这样一个事实,不是所有三维模型的视点都是同等重要的。自适应聚类方法在320面多面体的每个面的中心上放置摄像机获取初始图集,基于自适应聚类方法提供1组最优的二维视图选择,形状复杂程度不同的模型得会到1～40不等的视图选择[27]。对于什么视图是最优的问题,用视点熵的方法,最好的视点是具有最大熵的视点[28]。也有语义驱动[29]或Web数据驱动的方式选择符合人类视觉的最佳视图[30]。在自动选择3D模型最具代表性的视图任务中,可见面积比、轮廓长度、曲率熵等都可以评估一个视图的优点,Dutagaci的评估方法中,在正8面体细分后的测地球上设置258个视点,以3D模型视点与人类评价最优视图间的测地距离来衡量差异,这对我们衡量不同模型间的距离很有启发[31]。

而随着深度学习的兴起,多角度视图识别三维模型的方法也有了很大的发展,最具代表性的工作是Su提出的多视图卷积神经网络(multi-view convolutional neural networks,MVCNN)[32],他们将模型直立放置，虚拟摄像机放置在模型周围每隔30°的12个位置，再向上抬升30°对准模型中心获取视图，然后又与从正20面体每个面中心看向质心的20个视点旋转0°、90°、180°、270°得到的80个视图做比较，发现仅需要12视图,但在结论中提出2D视图的组合仍是需要探索的问题。在更深入的泛化能力研究中,他们又发现黑色背景的数据能获得更好的效果,且MCVNN方法使用的形状信息大部分位于对象的边缘,但实验中的视图选择依然是12个,并未有所改进[33]。除此之外,也有不少深度学习的方法,多数是关注网络结构的改进，提升数据集的识别精度[34-35],其中Liu的研究发现3视图足够表述特征,在ModelNet40[36]数据集上的识别精度已达到98.5%,提出后续考虑自适应选择视图数量[35]。在三维模型检索的比赛中,也更多使用均匀采样的视图,比如SHREC2020[37]基于单目图像的三维物体检索的赛道使用的数据集也沿用MVCNN的12视图的选择。

综上所述,基于多视图的传统和深度学习方法在视图选择上有均匀选择与最优视图选择两种途径。在深度神经网络进行识别的算法中多以均匀视图选择为输入,且在40分类127 915个3D模型的ModelNet数据集上已近乎完全识别。而最优视图的选择侧重于研究计算符合人类视觉的算法。本文研究一种最优视图计算算法,并使用MVCNN验证计算出一组视图对3D模型区分能力。为了对比本算法提供视图的优势,在ShapeNet-V2[38]中选择240类19 712个模型，对比均匀视图与我们的一组最优视图在MVCNN上的识别精度,结果表明相较多数算法中12与20均匀视图选择,我们的16视图精度都高出近30%。

2 本文方法

本文研究方法遵循“相似的3D模型,都具备相似的一组最优观察视点”，由于3D模型姿势归一化已有多种方案解决,而且一些优秀的数据集都提供了具备一致规范方向的模型,在ShapeNet-V2中还提供了丰富的注释信息,比如标注了模型的正面[36,38]。因此，本文不讨论模型归一化问题,而是在已刚性对齐的3D模型上分析,得益于前人的工作,避免了模型归一化误差对识别精度的影响,更专注于分析识别算法的精度。图2是本算法的整体流程,首先在均匀的密集视点上计算出三维模型的一组最优观察视点,并通过视点的测地距离衡量模型的差异性,构建精细分类数据进行验证。本算法能够对任意类3D模型提供一组独立的视图选择,而不是所有类的数据都用一致的均匀采集的视图。与其他视图选择对比实验结果表明,提供的视图选择,在多视图三维模型识别上具有明显的优势。

3 多层次视点描述符

3.1 多视图表示

文献[31]中提出定量评价最佳视图选择算法,使用了258个顶点测地球,提供接近连续的视点,以旋转不变的傅里叶描述符来计算视图间的差异,以测地球上点的测地距离来衡量两个视点的近似程度。我们使用类似的方式来定义测地球及测地距离来计算视点距离,不同的是,在获取更加密集的视点基础上,用倒角距离计算视图的差异,在半球的视点上建立不断细分三角形的分块方法,不同细分次数对应形成不同层次的最优视点组合,最终形成视点本身组合的特征向量即是视点描述符,用于3D模型的识别。

为了获取连续的视图,需要构造密集的视点测地球。从正8面体开始迭代细分,在迭代4次后获得1 026个顶点的视点球,如图3所示。此处不是从正12面体或20面体开始细分,是为了保证获取视点能够包含上、下、左、右、前、后的位置。又由于对称视点获得的视图轮廓线会有重复,我们仅渲染半球上的545个顶点的视图。这里获取的视点并不是细分后球体顶点的一半是由于半球包含了赤道上的所有顶点。

图3 构建测地球Fig.3 Construction of geodesic sphere

为了获取的渲染图能够保证同一模型在不同视角下的可比较性,我们需要设置摄像机参数来渲染1组视图。对已经模型归一化的数据,在测地球上的每个顶点位置放置摄像机,相机都向上并指向网格的质心。由于不同角度看到的剪影区别很大,根据模型包围盒最长内径来确定模型的最大缩放比例，以保证渲染的视图不会超出视野。最后,计算每个视图的重心,并移动到二维图像的中心位置,为避免移动后视图超出原视图范围,所有视图以最大移动的视图范围为标准进行视图移动,最终会得到一个3D模型的密集视图表示。

d(Ei,Ej)=

(1)

其中，d为两视图间的差异值；x和y是视图中图像边缘处像素坐标。

视图之间的差异我们采用倒角距离来衡量,倒角距离在进行图像边缘匹配时,对噪声、缩放、旋转并不敏感[39],在三维重建时也作为衡量不同模型差异的标准[40]。定义E是每个视点对应的图像边缘,Ei和Ej间的倒角距离值为d(Ei,Ej)。

在同一模型的不同角度获取的密集深度图是存在冗余信息的,如果利用SIFT计算密集深度图的特征则需要很大的计算开销,此处我们仅使用边缘信息来进行计算。每个渲染的深度图像用Canny边缘检测方法来获取准确的边缘信息,形成3D模型一组密集的不同视角的边缘图像。

3.2 多层次分块

为了能够完整地描述3D模型,设计能够不断分块的视点提取方式，算法步骤为：

输入 密集视点V，

输出 各层级视点v′。

Step1第1层级的视点都是上、前、左、右、后把每1/4半球设置为1个初始分块,每个分块中有3个视点。在曲面上进行视点的分块并不容易,此处建立曲面上点与平面上点的一一对应关系,定义曲面上的视点集合为V，而v是每一个视点,v∈V,以3个初始点确定的平面为P,映射规则f是球心与球面上的点v的连线与平面P交点,得到集合p,则f:V→P′是双射的,曲面上的点分块变为三角平面上的点后进行分块。

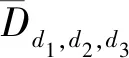
(2)

Step3在三角平面P上,以公式计算V对应Pi为种子点,以新种子点与原先的3个初始点连线分割三角形,形成新的3个三角形。

Step4返回步骤2,重复步骤计算下一层级三角形分块。

如图4所示,右上半球的3个初始视点为上、前、右，如图所示在1/4半球上的三角分块情况,黑色点是初始视点集合,红色点是第二层级选出的种子点,蓝色点是第三层级的种子点,黄色点是第四层级的种子点。每层计算的种子点对应的V的位置组合成的特征向量形成多层级描述符。在计算种子点时会存在落在三角形边线上的情况,但这并不影响继续分块,只是其中一个三角形退化为直线上选择种子点。可见在第四层时分块的三角形已经包含较少的数据点,如果再进行深入层级的分割,那么在建立顶点模型时应获取更密集的视图。但注意这只是1/4半球,四层计算的种子点已经有52个,在5.1节与5.2节的分析中我们对比了第二、三、四层的情况,认为三层形成的描述符足够区分常见3D模型。

图4 1/4半球分块Fig.4 Block of quarter hemisphere

3.3 相似度计算

3D模型的相似度定义为计算1组视点集合V之间的差异,定义3D模型的MLVD层数n为，用一个m行3列的二维向量来表示MLVD,以视点集合在测地球上的测地距离之和后取平均来测量距离,由于第一层级的视点在任何时候计算对应的测地距离都是一样的,所以并不需要前、上、左等6个视点的坐标。则m可根据公式计算，

(3)

可见,MLVD具有直观的语义,能够明确给出最优的一组视点位置,而且由于在归一化基础上的测地球上定义视点,MLVD是平移,缩放不变的,又由于倒角距离对噪声不敏感,所以也具备很好的抗噪性能。

4 细粒度分类数据

文献[33]研究MVCNN泛化能力的方法中,把Modelnet的40类数据集的训练数据分为10、100、1 000的均衡数量进行训练。在训练数据选择每类10个的400个模型4 800个视图及测试集为2 468个模型29 616个视图的实验中,识别精度达到77.8%,而在使用整个训练数据进行训练时识别精度达到95%。可见在测试集数量一样的情况下,训练集的多少影响了3D模型的识别精度。本文为了体现MLVD提供的视图具备的优势,选择更精细分类进行验证,从ShapeNet-V2中挑选分类数据进行对比试验。

ShapeNet-V2中每个类别内的3D模型有一致的刚性对齐,都是竖直的并注释了正面。55个大类中的模型数量从56个到6 778不等。每个大类会分为更细粒度的一些子集,最细粒度的子集数量仅有1个(比如chair子集中的armchair中的子集captain′s chair)。由于每个类的数据并不是完全分给每个子集的,比如rifle大类中有2 373个模型,子集carbine173个,sniper rifle729个,还有1 471个未细分类。实验中为了得到更多的分类并体现类内数据的不同,把父类与子类的数据当成不同的类来处理,挑选出每类多于10个模型的分类数据,每类保证10个模型作为训练集,每类的测试集分为1到150不等。即训练集为2 400个模型,测试集为17 312个模型。

在5.1节类内比较实验中使用类别car的ambulance子集的72个模型进行分析,5.2节实验中每个类随机挑选一个模型共计338个模型计算相似度(此处不受模型需超过10个的限制,用了ShapeNet的所有类)。实验结果分析中,仅改变输入数据不改变其他神经网络的超参数进行结果评估,输入视图采用文献[33]中的12个及数量更多的20面数据进行对比。

5 类内和类间相似度对比

5.1 类内层深度对比

类内数据我们比较了3种不同层级的情况,类间数据我们用MLVD-3进行比较,在MLVD-3上,类内和类间数据差异明显。

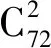
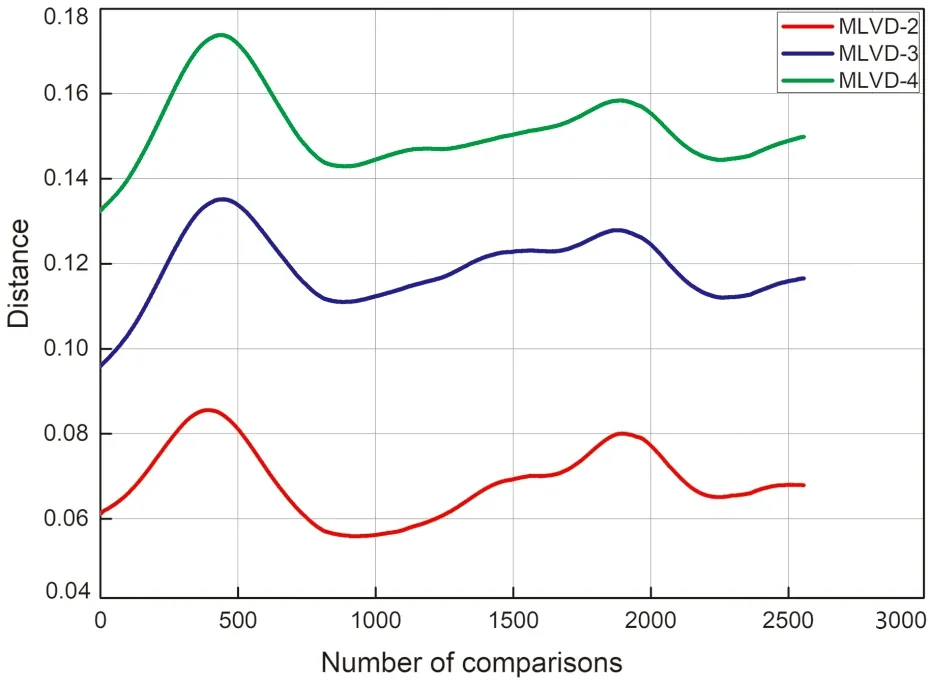
图5 不同层级的模型相似度Fig.5 Model similarity at different levels

5.2 类间数据的相似度对比

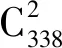
类间差异比类内差异平均值大43%,类间最小值存在是由于实验中把大类和子类当做不同的类来处理,会存在少量非常近似的模型,但从整体的数据来看,类间数据的差异非常明显,说明MLVD对模型的区分度很强。

表1 类内和类间相似度对比Tab.1 Intra class and inter class similarity comparison

6 实验结果及分析

文中所有数据来自ShapeNet,算法由Matlab实现,多视图卷积神经网络识别3D模型在6×Intel(R)Xeon(R)CPU E5-2678 v3 @ 2.50GHz,显存11G,NVIDIA GeForce RTX 2080 Ti,62 GB内存环境中实验。

6.1 识别精度的提升

为了验证MLVD对3D模型的识别能力,在MVCNN上使用3种不同的输入视图进行对比,测试集远大于训练集的数据上进行试验,这样的分法必然对提高识别精度不利,但却能体现视图选择的差异。原算法实验中的类别数由40变为240，不改变任何其他设定,测试3D模型识别的精度。实验设计中,12视图使用MVCNN中的方式,向上30°均匀获取,16视图是我们算法提供的,20视图是12面体顶点采集的视图,视图分辨率都是224×224,都把背景改为黑色。已经验证深度图像带来改进,对比时使用效果好的深度图,而16和20都仅使用边缘数据。训练数据采用随机水平旋转和不旋转来测试视图对精度影响的稳定性。如表2所示,由于测试集远大于训练集并且分类数量较原实验增大较多,精度并不是非常高,但可明显看出MLVD-16提供的视图与文献[33]的12及文献[24]的20视图选择识别精度非常接近,而本文的16视图选择在训练时不论是否进行随机水平旋转,都提升了近30%。

6.2 识别率分析

我们进一步分析了识别有误的数据,如图6所示。6A是未随机水平旋转的,6B是进行随机水平旋转的,横轴是计算错误率区间,纵轴是分类数量,12和20视图的错误分类基本持平,16视图明显低错误率的分类数量多,而高错误率的区间类别数少。我们发现，错误率高的数据有两个特点：①测试数据少(在数据集的细粒度分类中总共只有12个模型,2个模型当测试数据)。②测试数据中同一类数据形状差异明显的,比如错误率最高的Webcam类中存在圆的相机或方的相机。第一种情况在数据量大的情况下会改善,而第二种情况,基于形状来识别是很难改善的。

表2 不同输入视图在MVCNN上的识别精度对比Tab.2 Comparision of recognition accuracy of different input views on MVCNN

图6 错误识别数据分布Fig.6 Error identification data distribution

7 结语

本文提出一种新的3D模型描述符,该方法可以以不同分层深度的视点组合来描述3D模型,在连续的多视角视图中以倒角距离来衡量视图间的差异,通过最优目标函数的计算来得到每一层的最优视点,并以测地距离来计算模型之间的相似度。在实验中对层深的选择,类间数据的区分能力进行分析,并在细粒度分类数据上对比测试视图对识别精度的影响,得出均匀的视图选择很难再提升识别精度,而本文提供的视图具备明显的优势。MLVD具有缩放,平移不变性,对噪声不敏感,且具有直观的语义,易于为其他相关应用提供支持。