可调螺距螺旋桨螺距变化对轴系振动的影响

张 梦，朱汉华，李昭辉，门 皓，朱志鹏

(武汉理工大学 能源与动力工程学院，湖北 武汉 430063)

0 引 言

在一定条件下，使用定距桨的船舶在航行过程中，不仅能够通过调节功率达到想要的航行速度，同时螺旋桨的工作效率也能达到最适宜的值。但是螺旋桨在实际运转的时候，会面临各种各样的工况，其工况的不同会引起周围环境的变化，这就导致无法在各类工作状态下确保最大程度的发挥其功率[1]。而可调距螺旋桨则可以通过调节桨毂中的一些调距机构来调整螺旋桨的螺距，使得在不同工况下，达到主机的功率都能得到充分利用的效果，并能去掉整套换向装置，减少机构的复杂性，轴系便能够更好地适应复杂多变的工况[2-3]。因此，在实际应用中，可调距螺旋桨已被越来越多地应用到各种复杂的工况下，尤其是对于操纵和停船性能要求高的船舶。

最近几十年以来，可调螺距螺旋桨因其性能的优越性逐渐被越来越多的船舶制造行业投入使用，这从某种程度来说促进了船舶螺旋桨研究领域的专家和学者对这一类螺旋桨的研究。Cheng-zhang GU等[4]采用大型通用有限元分析软件Ansys对螺旋桨变压下的水动力性能（适航性、操纵性、快速性）进行模拟分析。胡磊等[5]采用CFD方法研究了可调距螺旋桨的敞水性能，而且得到的仿真结果和实验得到的数据对比结果高度一致，从而证明了计算模型的可靠性。张永坤等[6]分析了可调距螺旋桨的螺距角变化对离心力转叶力矩系数的影响，并通过实验验证了该力矩求解的可靠性。赵威等[7]对承受特定负荷的桨叶螺距、侧斜、拱度及纵倾等方面的优化设计进行研究，并对优化后的模型进行粘性流体动力学仿真验证。叶礼裕等[8]以DTRC系列桨为研究对象，在研究中融合了粒子群优化理论和面元法理论知识，更深入地探究了不同螺距拟合方式对螺旋桨产生的影响。Jeung-Hoon Lee[9]，Chen Kai等[10]研究了变距螺旋桨螺距角变化规律对螺旋桨水动力特性的影响。

本文将某集装箱船的推进轴系及可调螺旋桨作为研究对象，采用Ansys软件中的Fluent模块来仿真计算螺旋桨在淡水中运转时所受到的压力载荷，并通过流固耦合面施加到结构场中桨叶的表面，对轴-桨组合结构进行有预应力的模态分析及谐响应分析，再通过比较不同螺距下轴系固有频率和振型的变化，探究不同螺距角大小对尾轴振动性能造成的影响。

1 螺旋桨流场激励力分析模型与计算方法

1.1 理论模型

1.1.1 湍流模型

螺旋桨旋转时，其周围湍流流场复杂多变，为保证计算精度，需要选定合适的湍流模型，目前主流的是Standardk-ε湍流模型，但是其对曲率较大的模型仿真尚有不足，而对于本文研究的对象来说，RNGk-ε湍流模型因其对涡流或旋流等复杂模型具有较好的仿真效果，因此本文采用这一模型进行仿真，且该模型对湍流漩涡的计算精度也更高[11]。该模型利用N-S方程[12-13]进行运算，其方程描述如下：

RNGk-ε湍流模型的k方程

RNGk-ε湍流模型的 ε方程

式中：αk为k方程的湍流普朗特数；Gk为由于层流速度梯度影响而引起的湍流动能；Gb为由浮力而引起的湍流动能；YM为波动型膨胀造成的可压缩湍流动能耗散率；Sk为k方程的修正系数；αε为ε方程的湍流普朗特数；G1ε,G2ε,G3ε为 ε方 程的常量；Sε为 ε方程的修正系数。

1.1.2 桨-轴流固耦合运动方程

在仿真计算过程中，水对螺旋桨产生的压力必须要考虑在内，所以推进轴系和螺旋桨以某一恒定转速绕轴向旋转需要满足以下运动方程：

式中：M为结构质量矩阵；C为结构阻尼矩阵；K为结构刚度矩阵；u为 结构广义位移矢量；f0为流体对固体结构表面产生的压力矢量，f为结构力矢量。

1.2 仿真模型

1.2.1 模型建立

以某集装箱船的轴系和螺旋桨作为研究对象，螺旋桨为MAU型可调距螺距桨，轴桨材料性能参数如下：密度7 850 kg/m3，弹性模量E=2.1E9Pa，泊松比μ=0.3。

由螺旋桨的主要参数及经验公式计算得到螺旋桨桨叶的三维型值点坐标，并将其转化为Excel格式导入三维机械设计软件Solidworks中，建立螺旋桨叶实体和桨毂实体，通过圆周阵列命令将其与桨毂衔接，得到螺旋桨的整体几何模型，最后与尾轴进行装配。螺旋桨的主要参数见表1，尾轴主要尺寸参数见表2。

表1 螺旋桨主要参数Tab. 1 Main parameters of propeller

表2 轴系主要尺寸参数Tab. 2 Main dimension parameters of shaft system

1.2.2 流体域的建立及边界条件的设置

为了获得水中模态分布，流体域的建模是关键。轴桨组合结构在运转时，仅有螺旋桨部分和水有直接接触，据此建立流体域三维模型将螺旋桨包围起来。考虑到螺旋桨在水域中的实际情况以及计算工作量的大小，最终设置该流体域的直径为螺旋桨直径的3倍，如图2所示。流体域内部的介质为液态水，其密度为1 000 kg/m2， 粘度为0 .001 kg/ms。

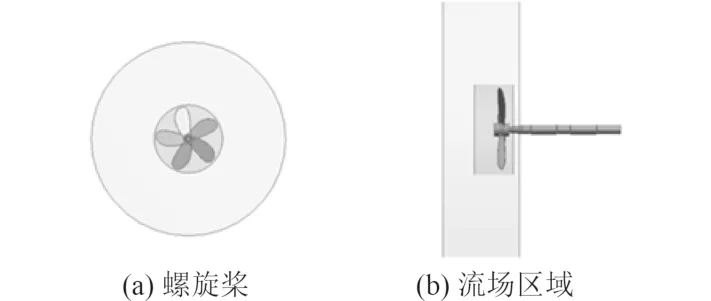
图2 流体域三维模型Fig. 2 3D model of fluid domain

网格采用曲率和狭缝控制函数来划分，流体域由静止域和旋转域组成，静止域为外部大圆柱体（直径19 960 mm，长6 000 mm），采用四面体的网格划分方法，旋转域为内部小圆柱体（直径7 000 mm、长3 000 mm）。螺旋桨叶梢和叶根处结构较为复杂，必须对其进行适当的加密，经过加密处理后生成的总网格数为219 942个，流体域网格如图3所示。

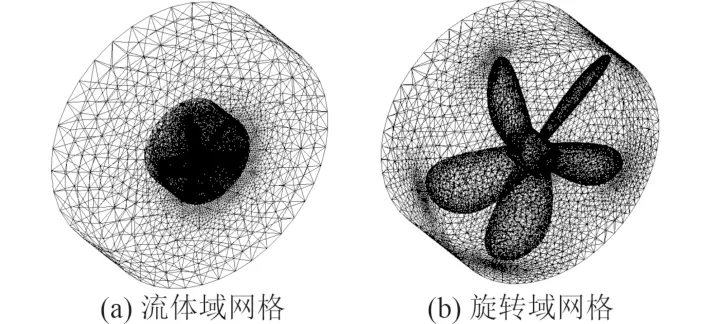
图3 流体域非结构网格Fig. 3 Unstructured mesh in fluid domain

在设置边界条件时，将入口来流速度设置为10 m/s来模拟船舶在水中航行时的来流速度，出口采用压力出口，压力为0；内部旋转域和外部静止域之间采用接触面形式来传递数据；旋转域绕Y轴旋转，转速为101.4 r/min。

1.2.3 固体域的建立及约束条件的设置

螺旋桨与尾轴组合的固体域模型采用四面体非结构化网格来划分，划分网格后的有限元模型如图4所示。对于轴桨组合在水中的模态分析，进行水压力作为预应力的模态分析时，将螺旋桨与轴接触面设置为固定约束，通过流固耦合面，将Fluent中桨叶在流体域中所受的压力载荷施加到固体域与流体域的接触面上，离心力通过对模型整体设置旋转速度来进行载荷的约束。轴承采用Workbench中虚拟轴承（Bearing）约束模拟，连接形式采用Body-Ground，考虑弹性支撑，水平刚度和垂直刚度均为 4 .6×109N/m ，不考虑轴承的交叉刚度及阻尼，结构的受力与约束如图5所示。

图4 固体域网格划分Fig. 4 Solid domain meshing

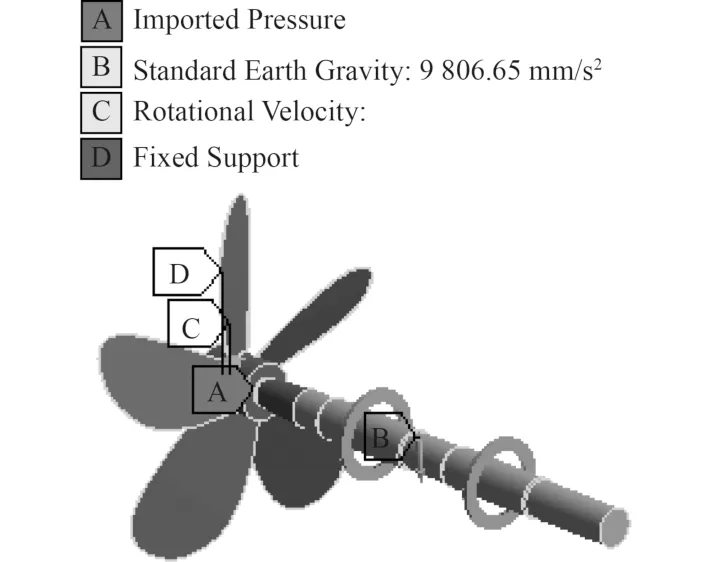
图5 结构的受力与约束Fig. 5 Structural forces and constraints

1.3 求解方法与过程

在Solidworks软件中建立不同螺距角下的螺旋桨和船舶尾轴的几何模型，导入到Design Modeler中添加流体域部分，在Fluent模块中采用 RNGk－ε湍流模型和Coupled耦合算法，进行敞水性能数值分析计算。随后在Static Structural模块中，进行各项边界条件、约束条件及计算方法的设置，将压力载荷载入到螺旋桨页面上，进行有预应力的模态分析和谐响应分析。

2 计算结果分析与讨论

2.1 模态分析

根据计算结果，对模型施加螺旋桨预应力及尾轴转速等约束，将螺旋桨与轴接触面保持全约束并考虑模型重力，进行有预应力的模态分析，依次改变螺距角，得到其前24阶固有频率，如表3所示。

由表3可知，该轴系在前15阶模态振型中共存在3种振动方式，即纵向振动、回旋振动和扭转振动。图6为螺距角为19.99.5°时的第21阶，22阶，23阶和24阶振型图。由表2及图4可知，因模型插入的虚拟轴承为各向同性，且忽略交叉刚度和阻尼，因此回旋振动的模态在垂直和水平方向上的固有频率总是成对出现的，如2阶和3阶、4阶和5阶、7阶和8阶、9阶和10阶、12阶和13阶、14阶和15阶、19阶和20阶，且在振型图上也分别表现为沿水平和垂直2个方向的振动。当可调桨螺距角逐渐增大时，其固有频率都随之减小。

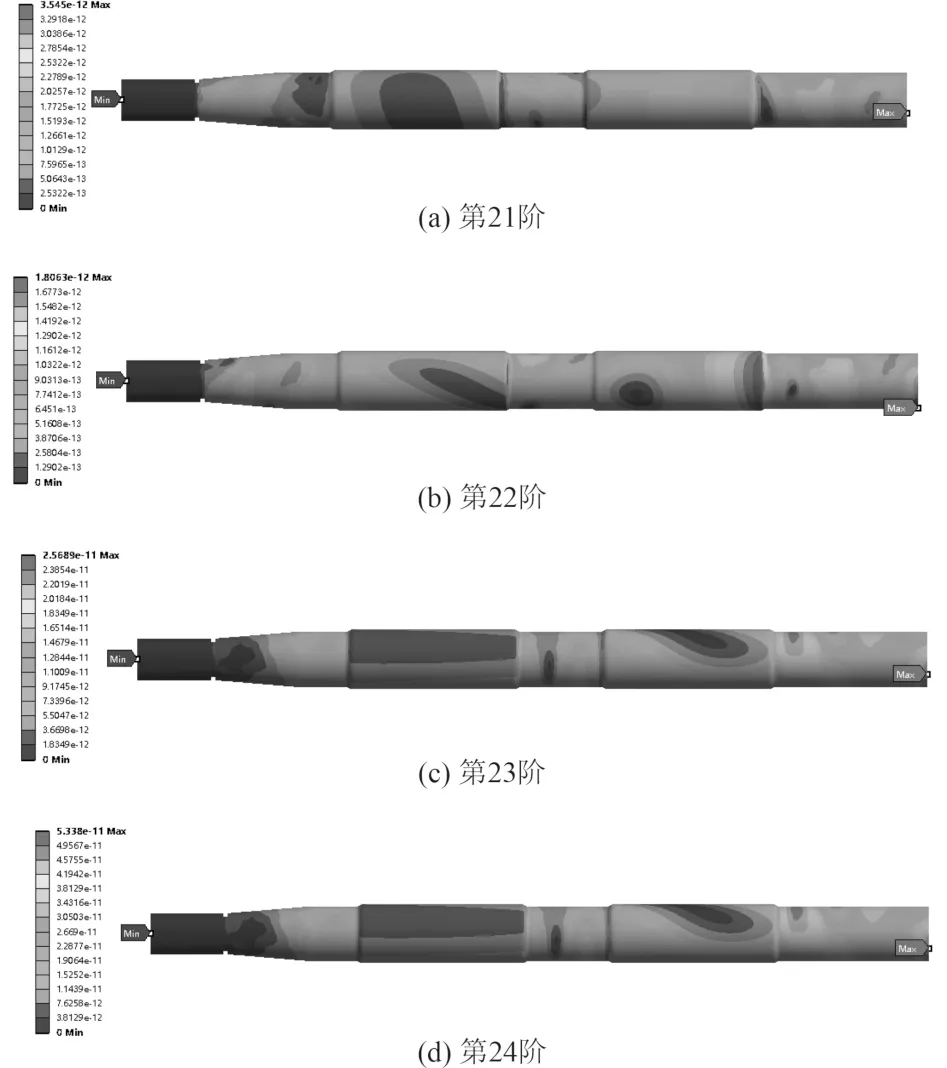
图6 轴系振型图Fig. 6 Vibration mode diagram of shaft system

表3 各螺距角下的艉轴固有频率及振动形式（Hz）Tab. 3 Natural frequencies and vibration form of stern shaft at different pitch angles（Hz）

2.2 形变分析

由图7可知，从不同螺距角的最大变形量进行综合分析，螺距角的变化对轴系的变形情况造成一定影响，当螺距角为19.900 5°时，整个尾轴的最大形变量达到最大，当螺距角为24.452 6°和28.620 2°时，整个尾轴的形变量都达到最小。

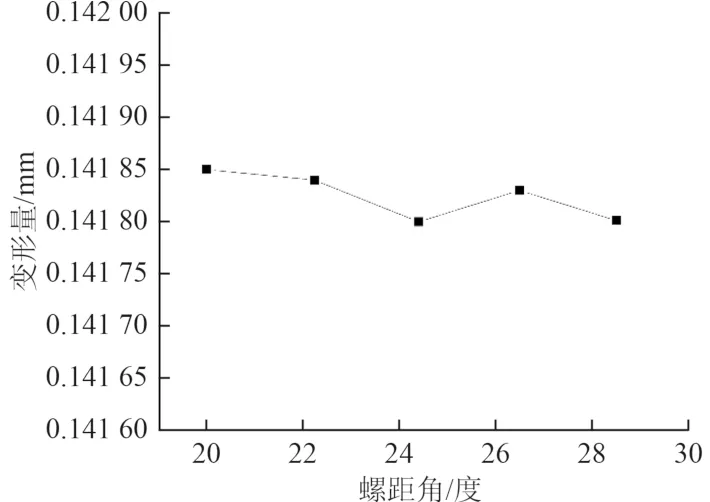
图7 各螺距角下轴系最大形变量Fig. 7 Maximum deformation of shafting under different pitch angles

2.3 谐响应分析

动态响应分析本质上就是轴系的强迫振动响应计算，即计算轴系不同螺距角下的动态响应。将在正常航行下所受的螺旋桨激励力施加到螺旋桨的对应节点上，扫频范围为0～50 Hz；分别计算船舶尾轴在到X轴、Z轴和Y轴方向位移-频率响应曲线如图8～图10所示。其中X方向为横向，Z方向为垂向，Y方向为轴向。

图1 轴-桨组合模型Fig. 1 Shaft-propeller combination model

由图8可知，各节点在某些固有频率附近会产生一定程度的共振，但共振幅值各不相同。在X方向上，当螺距角为19.990 5°时，主要在2.4 Hz，6.6 Hz，12.0 Hz，24.4 Hz和31.7 Hz附近产生较大的共振幅值；当螺距角为22.257 1°时，主要在6.7 Hz，12.0 Hz，24.5 Hz和31.8 Hz附近产生较大的共振幅值，当螺距角为24.452 6°时，主要在2.5 Hz，6.7 Hz，11.8.0 Hz，24.0 Hz和31.3 Hz附近产生较大的共振幅值，当螺距角为26.574 3°时，主要在6.7 Hz，11.8.0 Hz，23.6 Hz和30.9 Hz附近产生较大的共振幅值，当螺距角为28.620 2°时，主要在2.5 Hz，6.7 Hz，11.9.0 Hz，24.3 Hz和31.5 Hz附近产生较大的共振幅值。综上所述，在省去一些振幅较小的共振点后可见，X方向上主要在2.4 Hz、6.6 Hz、12.0 Hz、24.4 Hz和31.8 Hz附近产生较大的共振幅。

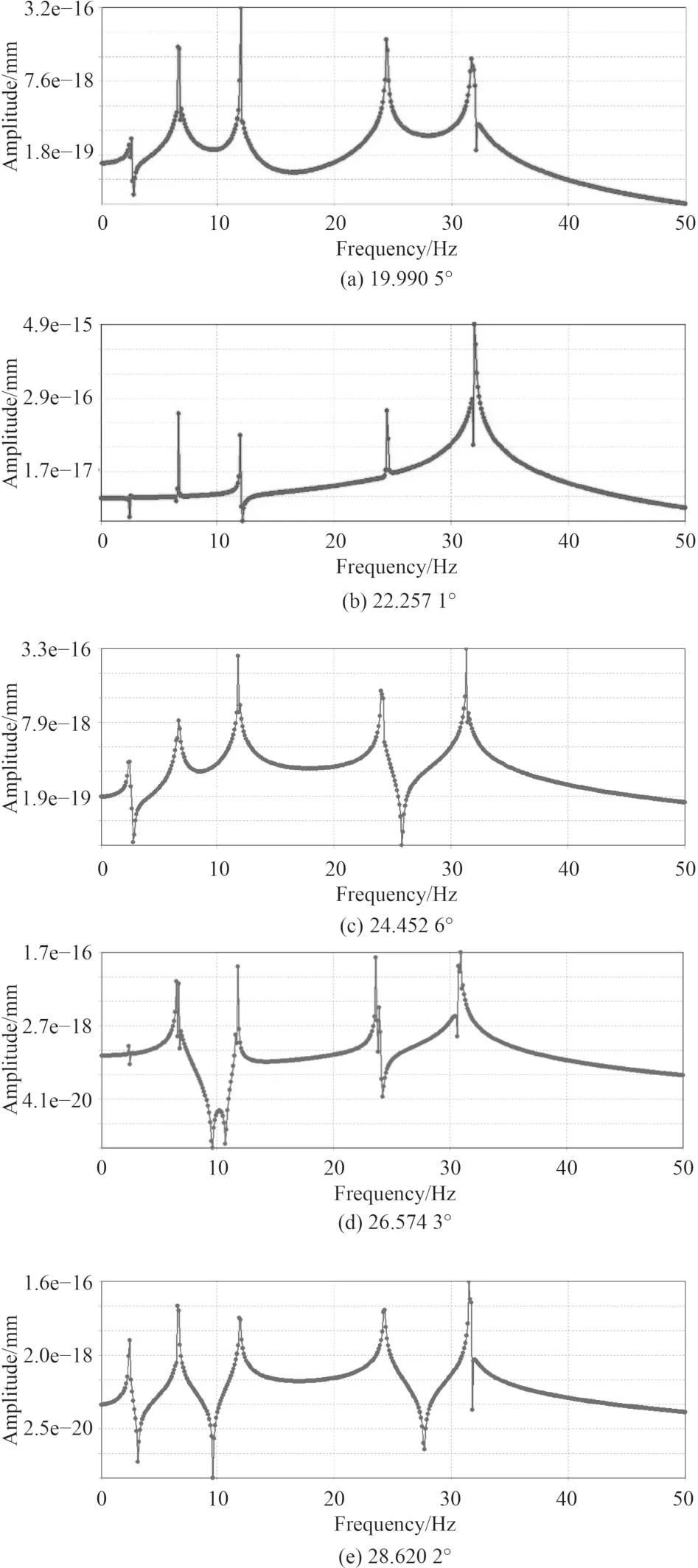
图8 X方向位移-频率响应曲线Fig. 8 Displacement frequency response curve in X direction

由图9可知，在省去一些振幅较小的共振点后可见，Z方向上主要在2.4 Hz，6.6 Hz，12.0 Hz，24.4 Hz和31.8 Hz附近产生较大的共振幅。

图9 Z方向位移-频率响应曲线Fig. 9 Displacement frequency response curve in Z direction

由图10可知，在省去一些振幅较小的共振点后可见，Y方向上主要在2.4 Hz，6.6 Hz，12.0 Hz，24.4 Hz和31.8 Hz附近产生较大的共振幅。

图10 Y方向位移-频率响应曲线Fig. 10 Displacement frequency response curve in Y direction

综上所述，船舶尾轴主要在2.4 Hz，6.6 Hz，12.0 Hz、24.4 Hz和31.8 Hz附近产生较大的共振幅。由图11可知，在0～35 Hz的扫频范围内，低阶频率处，振幅相对平稳，高阶频率处，振动的幅值产生最大值且振动幅值波动较大。尾轴在22.257 1°螺距角下更容易产生较大的振动，可通过合理的调节螺距角，以免出现共振现象。

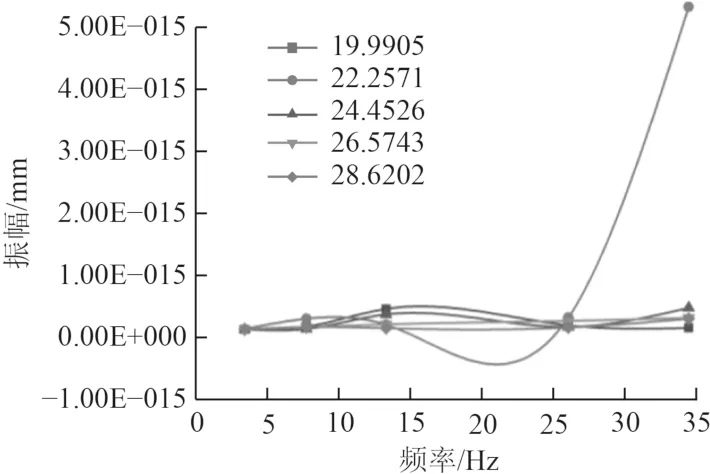
图11 不同螺距角下频率-振幅图Fig. 11 Frequency amplitude diagram at different pitch angles

3 结 语

本文运用流固耦合技术，通过螺旋桨-尾轴流固耦合的仿真分析，研究螺旋桨螺距变化对推进轴系尾轴的影响。仿真结果表明，可调桨螺距大小对船舶尾轴振动变形造成的影响并不能被忽略，得到的主要结论如下：

1）在一定范围内，随着可调桨螺距角的逐渐增长，尾轴的固有频率逐渐减小；

2）对于给定的研究对象，船舶尾轴主要在2.4 Hz，6.6 Hz，12.0 Hz，24.4 Hz和31.8 Hz附近产生较大的共振幅值，为提高尾轴使用寿命，尾轴激励频率应避免上述频率；

3）对于给定的研究对象，在一定范围内，尾轴在22.257 1°螺距角下更容易产生较大的振动幅值，可通过合理的调节螺距角，以避免出现共振现象。