基于数学问题情境 培养学生探究能力

梁佳卉 刘敬红

摘要：新知构建中的数学问题情境，能激发学生的探究欲望;综合应用中的问题情境，能诱发学生的探究动力;实践活动中的问题情境，能增强学生的探究体验;学习评价中的问题情境，能提升学生的探究能力。在教师的引导下，通过问题情境，学生能逐步学会用数学视角去关注情境，积极投入到想象、预测、探索、推理和反思的数学学习活动中，在活动中提高探究能力，提升数学核心素养。

关键词：小学数学;问题情境;探究能力

数学问题情境是指能引发学生积极思考、主动探究、合作交流、归纳概括、实践应用的信息材料，是开展数学活动的环境，是产生数学行为的前提。数学学习的核心是学会使用数学思维，掌握数学的思维方法，而数学问题情境为学生探究能力的提高奠定了坚实的基础。实践证明，具有挑战性和吸引力的数学问题情境是引导学生开展观察、操作、猜想、推理交流等体验性学习活动的有效载体，是引导学生在充满问题、思考和研究的数学世界中去探索、去体验、去创造的有效途径。学生在问题情境中经历发现问题、提出问题、分析问题、解决问题的全过程，思维品质和探究能力会不断提升，对今后甚至一生的发展都具有重要意义。

随着义务教育课程改革的全面深化，问题情境的创设越来越受到教师的重视。创设数学问题情境作为一种教育观念的大转变，成了课堂教学中的一种“时尚”。然而，冷静地审视一些问题情境，有许多问题值得我们深思。那些强拉硬拽的情境贴附、凭空杜撰的生活情境、强制拔高的挑战问题，使情境创设变味、跑偏，成为无效情境，浪费了宝贵的教学时间。创设问题情境不仅要激发学生的兴趣，而且要引导学生用数学视角去关注情境，为学生创设思维、探究、想象、预测、推理和反思的过程，引导学生积极投入到数学学习活动中，在活动中提高探究能力，促进数学素养的全面提升。

一、在新知构建中创设问题情境，激发学生的探究欲望

问题是创新的基础，情境是探索和创新的源泉。新知构建环节的问题情境设计，要围绕课时的三维目标进行，以学生的生活经验和知识能力为基础，从知识建构的生长点出发，对教材进行加工和再创造。教师要设计一到两个能统领探究过程的问题，寓问题于学生感兴趣的情境中，引领他们亲历知识的迁移、生长、关联的动态过程，在不断的探索和交流中，获得数学的基本活动经验，在潜移默化中受到数学思想的熏陶。

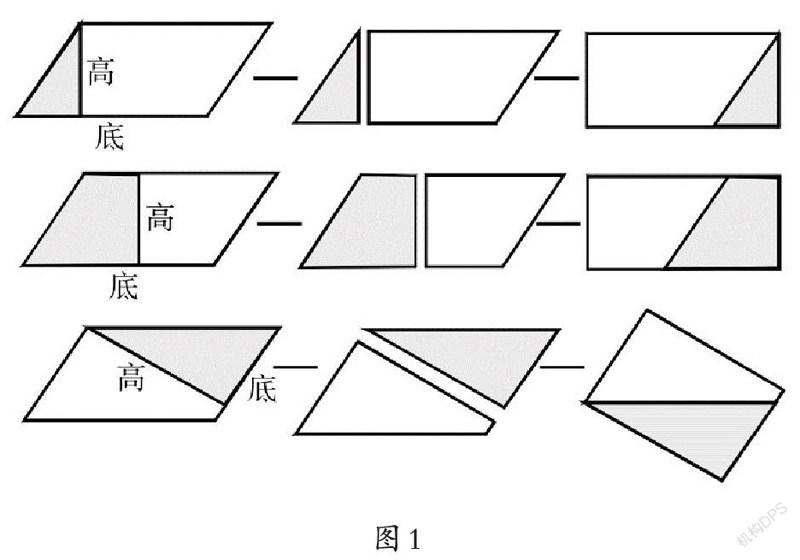
在“平行四边形的面积”一课的教学中，可以采用把数学问题生活化的设计策略，创设“比较平行四边形花坛与长方形花坛面积大小”的问题情境，引发学生猜想平行四边形面积可能等于底乘高，平行四边形的面积也可能等于邻边的乘积。怎样想办法来验证自己的猜想呢？学生的学习兴趣立刻被调动起来，他们兴趣盎然地投入到学具的剪拼，作图，组内交流做法、想法的探究活动中。结合实践操作，学生在体验知识形成的过程中，知道了转化后的长方形的长与原来平行四边形的底相等，长方形的宽与原来平行四边形的高相等，然后推导出长方形的面积等于原平行四边形的面积。（如图1）

通过这样的探究活动，使学生由被动的告知接受变为思考后的自主发现，对平行四边形面积公式的获得不再停留于形式的记忆，而是在操作、思考、交流、推理等过程中得到深入的理解，“转化”这一基本的数学思想方法也深深地根植于学生的头脑中。

同样，在“圆的认识”的教学中，根据学生在生活中对圆已经有一定的感性认识这一基础，教师可以采用生活情境数学化的设计策略，用课件呈现从古到今有代表性的交通工具图片，如马车、手推车、自行车、摩托车、汽车、飞机等。学生通过观察，很容易能发现它们的轮子都是圆形的，进而会深入思考，提出问题：轮子为什么设计成圆形的呢？这个问题反映了圆的本质。这一情境看似简单朴素，但却很容易激发学生提出数学问题，引发他们探索知识的欲望。

通过沿任意直径折叠圆形纸片（图2），学生发现：沿直径对折，图形两侧完全重合;圆是轴对称图形，任何直径所在的直线都是它的对称轴;中心点为圆心;通过画圆的半径和直径（图3），学生发现：圆有无数条半径和直径。进一步测量它们的长度可以发现，在同一个圆或等长的圆内，所有半径都是相等的，半径的长度是直径长度的1/2，直径的长度是半径长度的2倍。

在折、画、量等系列探究活动中，学生经历了知识构建的过程，掌握了圆的本质特征，知道了车轮设计成圆形，利用的就是同一圆的半径都相等的性质。这样的问题情境，不仅开启了数学与学生生活经验的链结，而且是学生探索和发现数学知识的载体。学生在探究的過程中，积累了如何去发现问题、如何去研究问题的经验，逐步学会用数学的眼光去观察生活。

新知构建环节有效的情境设计，一定是依托教材内容而创设的基于学生知识和经验的问题情境。它能有效架起沟通学生已有经验和所学数学内容的桥梁，学生在主动思考、自主探究与合作交流中去寻求解决问题的策略，进而形成认识、领悟思想方法、积累经验，体会数学的本质和价值。

二、在综合应用中创设问题情境，诱发学生的探究动力

动力和发展是相伴而生的。数学教学是学生展现思考历程、交流收获体会、激发创造潜能的过程。知识综合应用环节的问题情境创设，在秉承科学性、实用性的原则下，要注重知识的延伸点。情境中内隐的问题必须具有一定的难度和梯度，能够适应不同层次学生的需要。可以呈现一些具有剩余条件或缺乏必要条件的情境，让学生体验收集、整理、分析相关信息的过程，积累数学活动经验，提高分析问题和解决问题的能力。

在“三角形的面积”一课的综合应用环节，可以针对不同学生的学力水平，设计思维逐步递进的问题情境：请帮助农民伯伯解决问题。

课上学生完成情况反馈：

A组题毫无疑义，是三角形面积公式的基本应用，潜能生也能顺利解决。

B组题学生受习惯思维的影响，列出了45×42÷2、50×45÷2、50×45×42÷2等错误算式。教师组织学生以错误为资源展开探究，引导他们深入体会到面积计算的对应内核，即 “底必须与其所对应高相乘再除以2，得到的才是三角形的面积”，使他们深刻理解了三角形面积计算公式的模型本质。

C组问题的解决则一波三折，几乎所有学生开始都陷入了一筹莫展的境地，直观感受到直接解决问题可能性很小。对未知世界的好奇极大激发了学生探究的内在动力，从个体质疑到小组合作，学生动手折、剪、拼（双拼、四拼），不断调整解决问题的方案，最终迎来了“拨开云雾见明月”的豁然开朗。学生解决问题的方法大致有两类三种：

一是把等腰直角三角形对折，找出等腰三角形的高是50m，用100×50÷2=2500㎡求出三角形的面积。（如图5）

二是用两个等腰直角三角形拼成一个大的等腰直角三角形，得到大等腰直角三角形的两条腰都是100m，然后利用三角形面积公式，求出整个三角形的面积，最后再把它平均分成两份，就能求出等腰直角三角形的面积100×100÷2÷2=2500㎡。（如图6）

三是用四个等腰直角三角形拼成正方形，四条边的长度都是100m，利用边长乘边长，求出正方形的面积。再把它平均分成4份，这样也能求出等腰直角三角形的面积，100×100÷4=2500㎡。（如图7）

学生用图形对折、组合的方法，化未知为己知，使冗杂问题简化。这样的情境设计，有利于帮助学生对知识本质和规律的深入理解，发展学生思维的广阔性和灵活性。

综合应用情境中的问题设计，教师要时刻关注学生在探索、发现、应用过程当中的表现，引领他们学会利用已有的知识和经验联想、分析、归纳和类比，掌握研究的基本思路和解决问题的基本方法，促进高层次思维的发展和学生解决问题能力的形成。

三、在实践活动中创设问题情境，增强学生的探究体验

实践活动有别于学习具体知识的探索活动，更有别于课堂上教师的直接讲授。它是以问题为载体、以学生自主参与为主的学习活动。通过任务驱动可以引导学生从已知经验中不断生发出新经验、新方法，促进其认知结构的进一步概括化和系统化，促使他们对数学本质深入理解。

数学学科实践活动中问题情境的设计要注重问题的整体规划，可以是取自生活实践的真实问题，也可以是论证与探究数学知识的结论。通过问题载体和活动设计，为学生积极探索和发现提供条件，让他们在“做”“观察”“实验”“探究”等一系列的活动中展示自己，发展自己，学会发现，学会探究，学会实践，应用意识和问题意识有明显提升。

在学生已经掌握植树问题规律的基础上，可以开展主题实践活动“校园设计师”。这一现实问题情境，让学生激动不已，他们纷纷发表自己的观点，很快列出需要设计的区域（试验田、花坛、甬路、跑道、操场、足球场、篮球场、铅球场地），计算各区域周长和面积所需要测量的数据，每个区域具体的设计方案，各区域辅助设施（如路灯、长椅、绿植、鲜花）的市场价格及调查的方法。通过动手测量、实地调查、查阅资料、合作交流、推理论证等丰富的活动，从中收集整理了解决问题所需的数据，学生理解了数学事实，积累了数学活动经验，体验到了成功的喜悦。特别是当独具匠心的设计通过精彩的多媒体呈现在大家面前的时候，教室里沸腾了，学生探索问题的热情更高了，一份份不够完美但饱含热情和心血的设计方案不断出现。这样融问题、思考、实践、提升于一体的实践活动，最大限度地增强了学生的探究体验，这是师生共同创造的和谐的、具有多种活动形式、多种过程体验及多种评价方式交融浸润的过程。

在“圆柱体的体积”之后，我们设计了一个综合实践活动“旋转的长方形”，以“长与宽之和为定值的长方形的一边所在的直线为轴，旋转一周得到的多个圆柱的体积大小”为研究对象，以此为主题，创设了如下问题情境：

一条长24厘米的铁丝，用它围成长与宽均为整厘米的长方形。以此中的一条边所在的直线为轴，旋转一周得到的多个圆柱体的体积是否相等？

学生根据题意，很快整理出24厘米的铁丝能围成11种长方形。（如表1）

以此中的一条边所在的直线为轴旋转一周，得到的11个圆柱体体积的大小都相等吗？如果不等，是否存在一定的规律呢？未知悬念充分激发了学生探究的动机与兴趣。

在接下来的小组研究验证过程中，学生全力投入到计算、交流、归纳总结的过程中：有的小组先把数据化繁为简，从长与宽的和是6厘米、7厘米的长方形入手，然后循序增加到长与宽的和是8厘米、9厘米，最后研究長与宽的和是12厘米。

多组研究数据汇总后，学生发现：当半径是高的2倍时，圆柱的体积是最大的。因为这是不完全归纳法得到的结论，学生还不能坚定自己发现的正确性，后续的关联应用性问题使他们对结论的认识在比较中得以提升。在本次实践活动中，学生始终保持着旺盛的探究热情，在猜想、验证和发现中不断自我突破。从具体到抽象、从特殊到一般，逐步揭示知识之间的内在联系，并用数学形式表达规律，这种建模策略的理解和掌握，将学生的思维和推理提高到了一个新的水平。

在实际教学中，教师要注重设计这样的活动，让学生在对问题的深入思考和问题解决过程中，逐步深化对数学的认识，发展创新意识和实践能力。

四、在学习评价中创设问题情境，提升学生的探究能力

评价是数学课程实施中的一个重要环节。评价是对学习结果的测试，是对学习过程的回顾。在对学生进行数学能力评价时，必须注重问题情境的设计，在解决具体问题的过程中对学生进行整体评价。情境设计应该在深层次解读文本的基础上，围绕评价的重点元素，设计学生感兴趣的情境，内嵌难度适中、能充分暴露学生思维过程的问题，以此评价促进学生探究能力的提升，促进学业质量的提升。

在学完周长和面积的内容后，我们结合本地旅游景区资料，设计了如下的评价活动：

天香源生态农场准备用长10000米的篱笆围出一个边长为整米数的长方形山楂种植园，怎样围面积最大？面积是多少？

（1）列举四个满足条件的长方形，记录下长方形的长、宽和面积（可以使用计算器），并按照一定顺序把数据整理填写在表2中。

（2）观察排列的结果：周长一定时，长方形的长和宽发生变化，面积会相应的发生怎样的变化。

（3）写出解决问题的思考过程及结论。

学习评价设计这样的问题情境，有助于考察学生的思考过程，更重要的是使他们的在这个过程中能找出解决问题的方法。从学生回答这些问题的过程中，可以清楚了解他们的数学学习水平，培养他们的科学研究态度。

任何解决数学问题的过程，都是一次非常具有挑战性的数学探索之旅。在这一过程中，数学知识的获得、数学技能的提高、数学思想的熏陶和数学活动经验的建立，都是悄无声息、潜移默化地发生着的。作为学习过程组织者、指导者和合作者的教师，精心创设有效的问题情境，能让学生由被动地接纳转化为主动地建构，让课堂充满思维的张力，让探究能力不断提高，促进积极主动、生动活泼、可持续地发展。

参考文献：

[1]史宁中.《义务教育数学课程标准（2011年版）》解读[M].北京：北京师范大学出版社，2012.

[2]黄毕年.巧设情境导新课[J].小学数学教师，2015（12）.

[3]朱志明.创设问题情境的五大误区[J].小学数学教育， 2007（12）.

[3]张国江.小学数学问题情境的创设[J].福建教学研究， 2013（3）.

（责任编辑：杨强）

作者简介：梁佳卉，葫芦岛市建昌县二道湾子乡小学中心校二级教师。刘敬红，葫芦岛市建昌县新区小学特级教师。