隔水导管复合群桩竖向承载特性

刘 润， 于健东， 梁 超， 万 军， 关 湃， 李翔云

(1. 天津大学 水利工程仿真与安全国家重点实验室， 天津 300072；2. 中海石油(中国)有限公司 天津分公司， 天津 300459)

0 引 言

海洋平台的建造成本是制约边际油田开发的关键。在现有平台结构中井口隔水导管通常采用钢管打入地基土的方式以起到隔离海水和循环钻井液的作用。隔水导管的结构和尺寸与钢管桩相似，且通常成阵列布置，数量较多。若适当考虑隔水导管的承载能力，将其部分甚至全部替代海洋平台的钢管桩基础，则可实现降低平台建造成本的目标。海洋平台井口结构通常包括隔水导管、表层套管、内部生产管及各管件之间的固井水泥环，如图1所示。

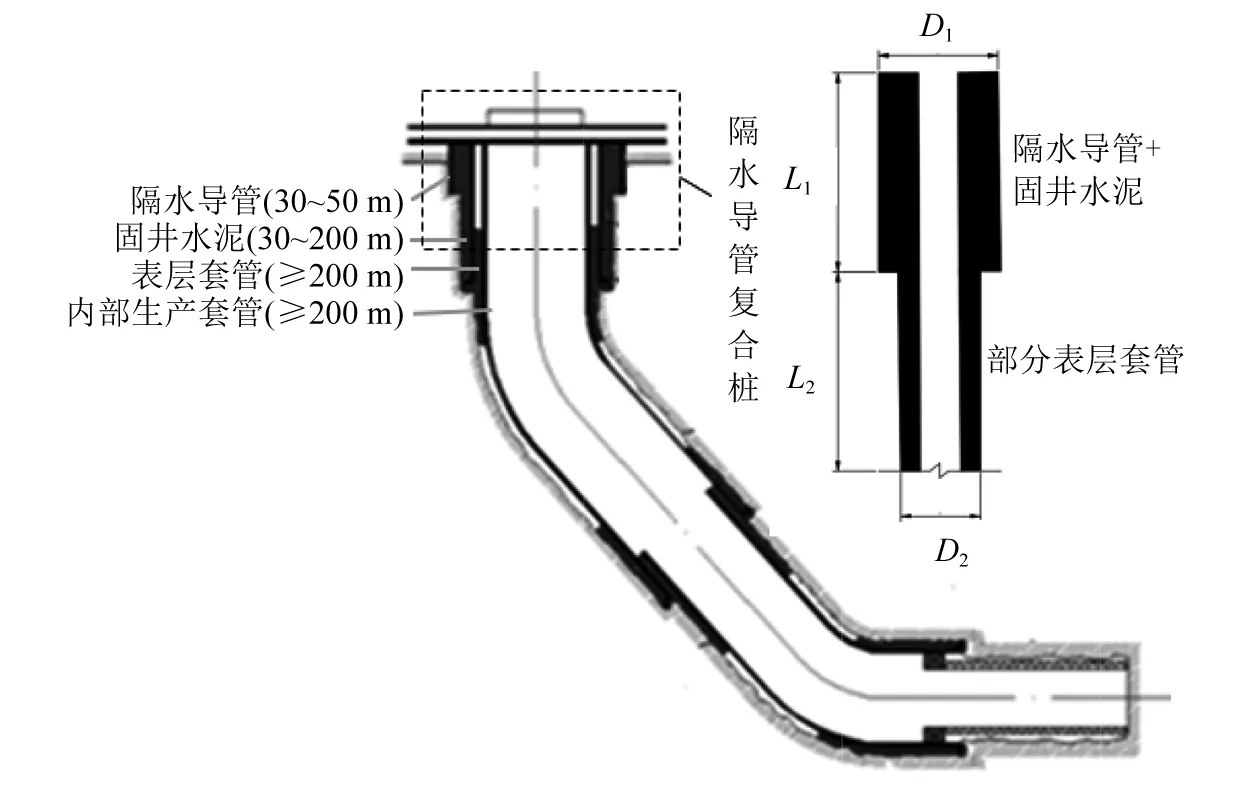
图1 井口结构示例

与钢管桩相比井口结构的入泥深度很深，且随着深度增加钢管直径不断缩小。隔水导管与表层套管通过固井水泥连接为整体，该部分的直径和入泥深度与普通钢管桩基础相当，因此考虑将该部分视为桩基础以提供承载力，称其为隔水导管复合桩，其中，上段包括隔水导管和固井水泥(长为L1)，下段包括部分表层套管(长为L2，外径为d)，隔水导管复合桩上段桩径为D1、下段桩径为D2，如图1所示。与普通钢管桩相比，隔水导管复合桩存在明显的变截面和中空结构。

目前将隔水导管作为平台的支撑已有初步应用，墨西哥湾海马系列平台和渤海湾无人简易平台有采用隔水导管作为支撑结构的先例，但未见系统的理论分析或计算方法。现有对隔水导管的研究主要集中在满足工艺要求的隔水导管最小入泥深度[1]及可打性[2-3]研究方面。考虑隔水导管承载性能的研究则始于2014年。吴雪峰[4]开展小比尺室内试验和有限元模拟以研究隔水导管的群桩承载性能。万军等[5]提出隔水导管复合桩的概念，并研究具有变截面特性的隔水导管复合桩的单桩承载性能及其影响因素。

海洋平台的井口结构通常成阵列布置，且随着开采工艺的改进和生产能力的提高，井口直径不断增加、间距不断缩小，如辽南井口平台30口井和埕岛油田平台井口间距大多为1.6～1.8 m，如图2所示。井口的密集布置导致隔水导管复合桩密集分布，桩间距通常小于2倍桩基础直径，这样的距径比已大幅低于桩基规范规定的最小界限。为合理利用海洋平台井口结构的承载能力，有必要对密集分布的隔水导管复合桩承载力及群桩效应开展研究。

图2 海洋平台井口群

本文针对隔水导管复合群桩密集分布的特点采用有限元方法模拟分析群桩基础的竖向承载模式与影响因素。基于隔水导管复合桩的变截面特点，推导隔水导管复合桩的群桩效应系数，并与普通钢管桩的群桩效应系数进行对比。

1 有限元分析模型建立

1.1 单桩基础数值分析模型与验证

为分析隔水导管复合桩极限承载力，基于Abaqus有限元软件建立模型。选取渤海地区常用隔水导管，尺寸如表1所示。

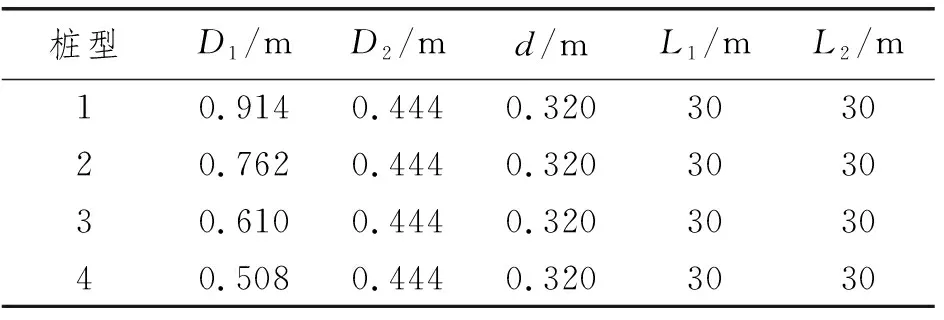
表1 隔水导管复合桩尺寸

结合复合桩存在明显的变截面和中空结构特点，建立复合桩单桩模型，如图3所示。为避免产生边界效应[5]，土体平面尺寸取20倍桩径，深度取1.5倍桩长。桩体采用线弹性本构模型，土体服从Mohr-Coulomb屈服准则，选用均质饱和黏土，不排水剪切强度Su取20 kPa，弹性模量E取500Su，泊松比取0.48。

图3 复合桩单桩有限元模型

桩体及土体网格属性均选择C3D8R，形状为六面体单元。土体顶面自由，外边界约束x、y方向，底面采用全约束。为反映桩-土界面相互作用时的接触情况，桩体与土体之间选用主动-被动面模拟，刚度较大的桩体为主动面、较小的土体为被动面，桩-土接触面中法向接触选择硬接触、切向接触使用罚摩擦公式，摩擦因数按文献[6]中的材料界面剪切试验研究取0.4。

为保证有限元计算结果的准确性，将不同桩型下单桩竖向极限承载力有限元分析结果与美国石油协会(API)规范法[7]结果进行对比。结合实际情况，复合桩内部不存在土塞，不会产生内侧摩阻力。竖向承载力由外侧摩阻力和端部环形截面阻力构成。利用API规范分别计算上段桩外侧摩阻力、变截面处端部环形截面阻力、下段桩外侧摩阻力和端部环形截面阻力，四部分之和即为复合桩单桩竖向极限承载力，如表2所示。由表2可知，有限元计算结果与API规范计算结果较为吻合，可证明有限元分析方法的可靠性。

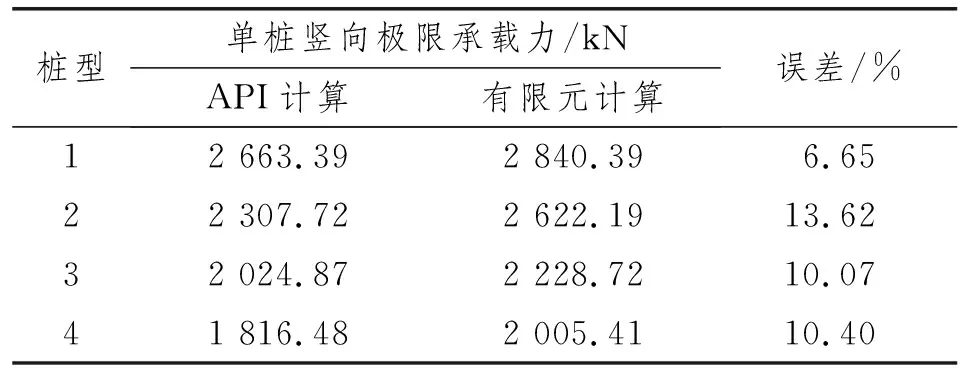
表2 隔水导管复合桩单桩极限承载力对比

1.2 群桩基础数值分析模型

以隔水导管复合单桩有限元分析模型为基础建立群桩模型。为模拟带承台工作状态，防止不同桩体之间不均匀变形导致结构提前破坏，在桩体上部设置加载板[7]，板厚取0.1 m，弹性模量设置为无限大，等效为刚体，其与各个桩顶面采用绑定连接。土体网格划分如图4所示。

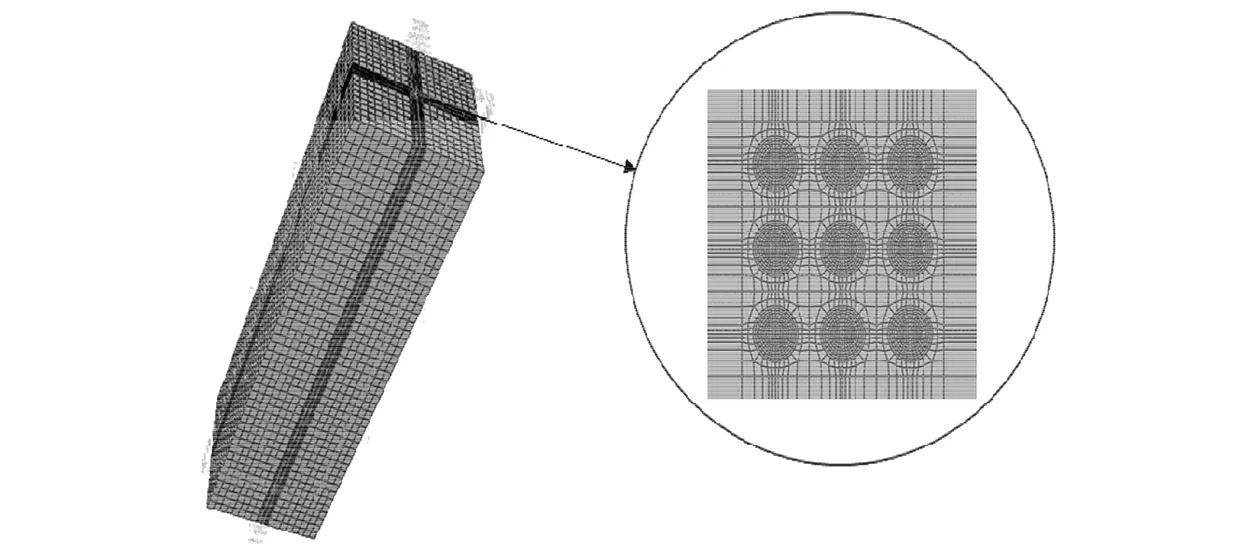
图4 群桩网格划分有限元模型

为分析复合群桩与普通群桩基础之间承载特性的区别，同时建立普通钢管群桩模型，普通钢管桩桩径与隔水导管复合桩上段桩径相同，桩长为隔水导管复合桩的总桩长。由于钢管桩的径长比较小，由文献[8]和文献[9]可知，当径长比小于0.02时，钢管桩内土塞基本完全闭塞，需按照闭口桩考虑，建立实心桩模型，尺寸如表3所示。

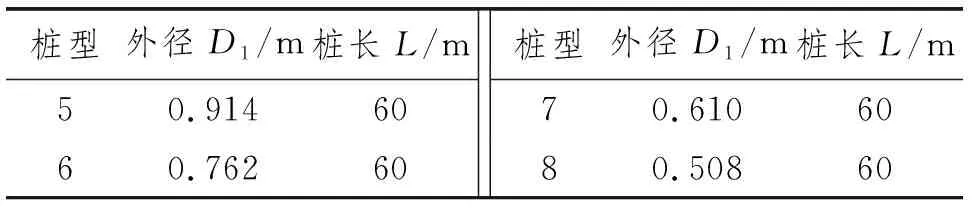
表3 普通钢管桩尺寸

2 隔水导管复合桩群桩效应分析

2.1 群桩效应系数与破坏模式

定义群桩效应系数η为

(1)

式中：Qg为群桩总极限承载力；Qs为单桩极限承载力；N为桩数。

研究[10]表明，群桩基础破坏模式分为整体破坏和非整体破坏，如图5所示。

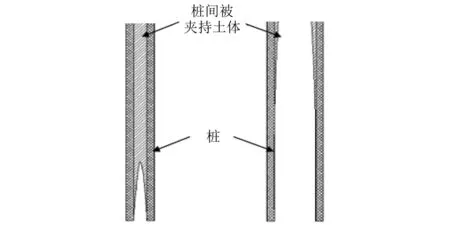
图5 破坏模式

整体破坏指各桩之间土体随基桩共同向下运动，等效成实体墩基进行工作，桩-土之间形成一个整体，剪切破坏面在群桩外围表面。非整体破坏指各桩相对独立，剪切破坏面出现在各基桩的桩-土之间。隔水导管复合群桩基础因上下段桩径不一，桩间距也不相同，从而与相同布置下普通钢管群桩基础破坏模式有所区别，以下进行详细讨论。

2.2 距径比的影响

定义Sa为相邻隔水导管复合桩间距，分析距径比Sa/D1对群桩基础竖向极限承载力的影响，建立1号～8号桩型在Sa/D1=1.5～6.0下的9根桩组成的群桩模型。图6为1号和5号桩型群桩基础在不同Sa/D1下的基桩平均载荷位移曲线。为了对比，图6同时包含单桩载荷位移曲线。

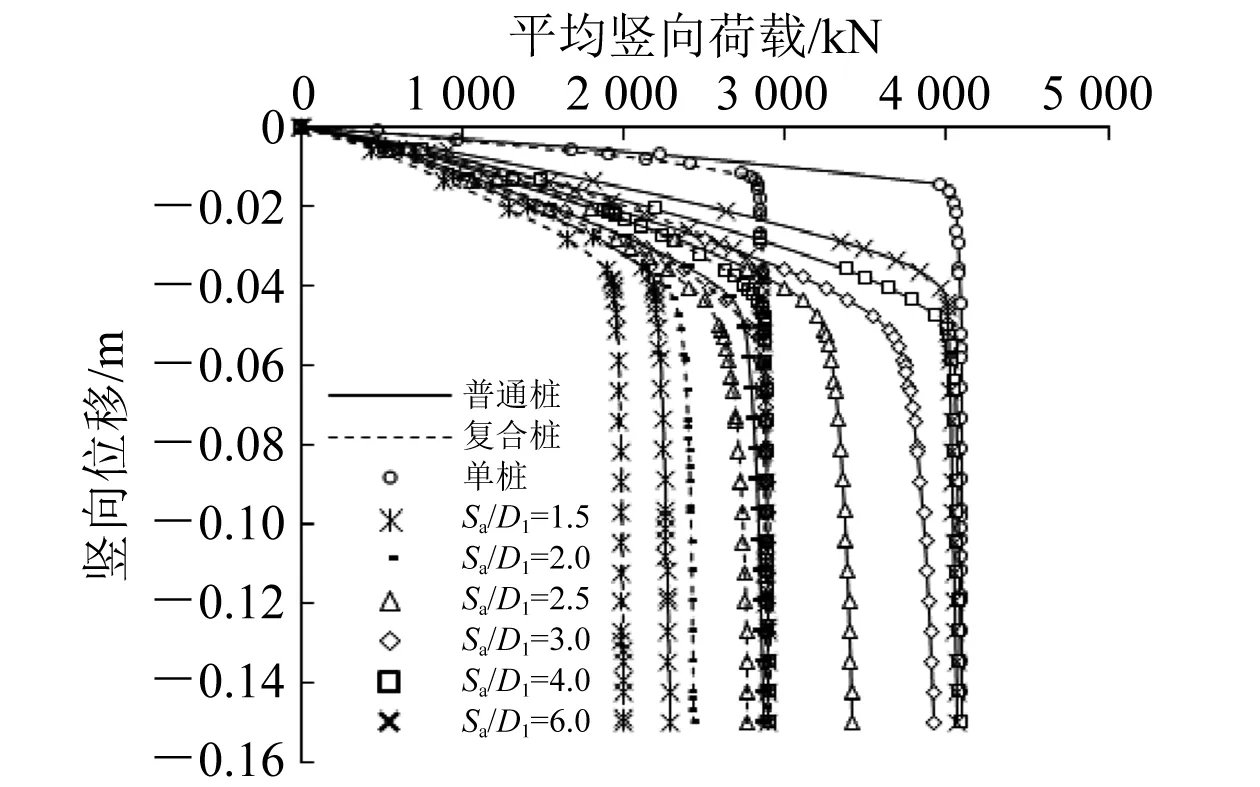
图6 不同Sa/D1下竖向载荷位移曲线

由图6可知，单桩的载荷位移曲线存在明显的拐点，群桩的载荷位移曲线较为平缓。因此，采用切线法[11]确定群桩的极限承载力。在不同Sa/D1下2种群桩基础的载荷位移变化规律相同，群桩基础平均极限承载力均小于单桩，且随Sa/D1的增大而增大；在相同载荷作用下群桩位移大于单桩，并随着Sa/D1的增大而减小。在桩长和桩径相同的条件下，隔水导管复合群桩极限承载力小于普通钢管群桩，这是由复合桩变截面以下桩径变小，桩侧表面积变小，侧摩阻力变小所致。在相同载荷作用下，隔水导管复合桩单桩比普通钢管单桩位移大，在群桩基础中，这种现象随着Sa/D1的增大而变小。

利用式(1)计算不同Sa/D1下2种群桩基础的群桩效应系数，结果如图7所示。由图7可知，在不同Sa/D1下2种群桩基础η变化规律均随Sa/D1的增大而增大，但均小于1。当Sa/D1较小时，η对Sa/D1变化较敏感呈线性变化；当Sa/D1较大时，曲线较平缓，当Sa/D1大于4以后，η接近1，且变化幅度较小，群桩效应减弱。文献[12]指出当群桩桩尖以上土层强度较小时，其应力扩散角和桩侧摩擦力均较小，应力重叠作用区域变小，在Sa/D1小于4的条件下才需考虑群桩效应，这与本文结果相符。在Sa/D1相等的情况下，隔水导管复合桩η较普通钢管桩略高，且随着Sa/D1的增大，这种差距减小，这是由隔水导管复合桩变截面以下桩间距增大所致。以1号和5号桩型为例，在Sa/D1=1.5～4.0时η相差为0.165、0.119、0.155、0.089、0.004，可见在相同情况下复合群桩承载力发挥更好。

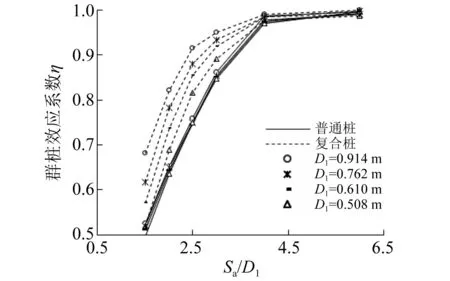
图7 不同Sa/D1下群桩效应系数曲线

在不同Sa/D1下，2种群桩基础达到极限承载力时的位移云图如图8所示。

图8 不同Sa/D1下群桩基础位移云图

取1号和5号桩型组成的群桩，2种群桩均对桩间土体存在夹持作用。普通钢管桩群桩在Sa/D1=1.5、2.0、2.5、3.0时桩土共同向下运动，形成整体破坏模式[13]：当Sa/D1=1.5时基桩夹持作用最明显，随着Sa/D1增大，夹持作用区逐渐缩小，主要集中在桩身中部区域；当Sa/D1=2.0时，基桩夹持作用变弱，夹持作用区位于桩体中下部；当Sa/D1=4.0时基桩夹持作用消失，呈现非整体破坏模式。隔水导管复合群桩在Sa/D1=1.5时呈现整体破坏模式，在其余工况下均为非整体破坏模式，基桩夹持作用仅出现在上段桩中部区域，且随着Sa/D1的增大逐渐缩小，在Sa/D1=4.0时消失。

图9为Sa/D1=1.5时的基桩桩身轴力随深度变化的曲线。

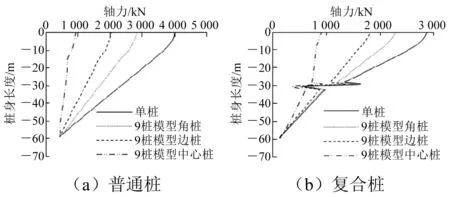
图9 Sa/D1=1.5时群桩基桩桩身轴力分布

由图9可知，各基桩桩身轴力均随深度呈减小趋势，隔水导管复合桩在变截面处轴力发生突变，原因是变截面处产生部分桩端阻力，力由此传入土体中。桩顶轴力从大到小排序依次为单桩、角桩、边桩、中心桩，单桩侧摩阻力发挥最为充分。究其原因是中心桩桩周土体受基桩夹持作用最为明显，桩土相对位移较小，侧摩阻力不能得到充分发挥。结合图8可知，普通钢管桩群桩的夹持作用发生在桩体中部，隔水导管复合群桩的夹持作用基本发生在上段中部。说明普通钢管桩的群桩侧摩阻力折减范围较大，隔水导管复合群桩侧摩阻力折减范围主要发生在上段桩，仅在Sa/D1=1.5、2.0时存在下段桩侧摩阻力的折减。普通钢管桩群桩中角桩、边桩、中心桩与单桩桩顶轴力比值依次为0.71、0.51、0.24，而隔水导管复合群桩分别是0.81、0.65、0.34，说明隔水导管复合群桩作业时各桩可以更好地发挥侧摩阻力。中心桩受桩间距影响最明显。

图10给出中心桩桩身轴力分布规律。

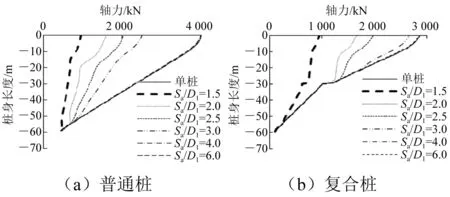
图10 不同Sa/D1下中心桩桩身轴力分布

由图10可知，普通单桩轴力从桩顶到桩端呈现逐渐减小趋势，复合桩在变截面出现明显的轴力突变，变截面承担了部分桩顶载荷并传入土体。

2.3 桩数的影响

图11为在Sa/D1=2.0工况下，1号和5号计算模型在不同N下的基桩平均载荷位移曲线。为了对比，图11同时包含单桩的载荷位移曲线。

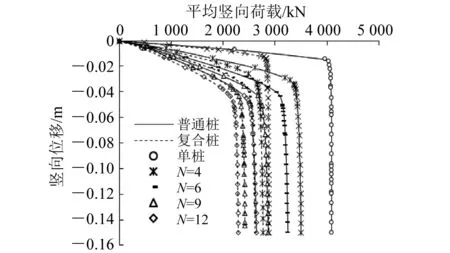
图11 不同N下竖向载荷位移曲线

由图11可知：在不同N下2种群桩基础载荷位移变化规律相同，随着N的增大，基桩平均竖向极限承载力降低；在相同平均载荷作用下，沉降量随N的增大而增大。

在不同N下2种群桩基础群桩效应系数结果如图12所示。

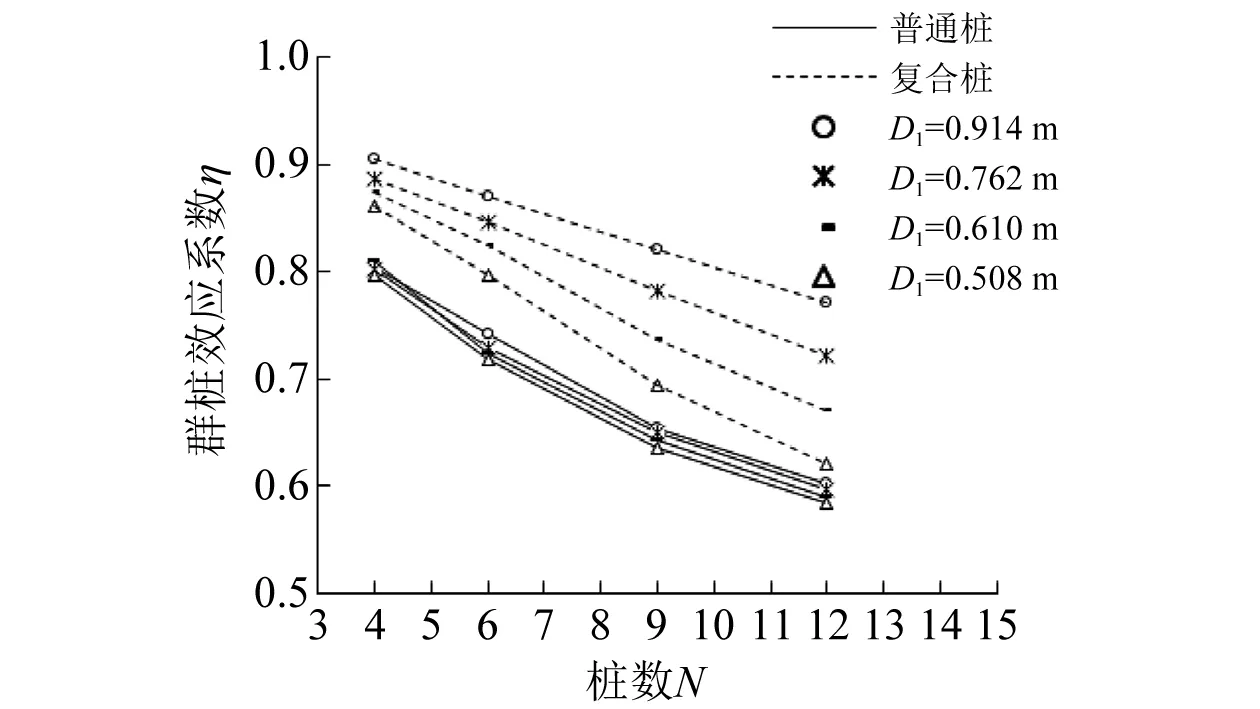
图12 不同N下群桩效应系数曲线

由图12可知，η随N的增大而减小，且均小于1。当N较小时，普通钢管桩η减小速率较快；当N较大时，变化速率放缓。隔水导管复合桩η对N变化更敏感，当N相同时，隔水导管复合桩η较普通钢管桩略高，且随着N的增大，两者差距增大。以1号和5号桩型为例，在N为4、6、9、12下η相差分别为0.101、0.129、0.168、0.169。

在不同N下，2种群桩基础达到极限承载力时位移云图如图13所示。

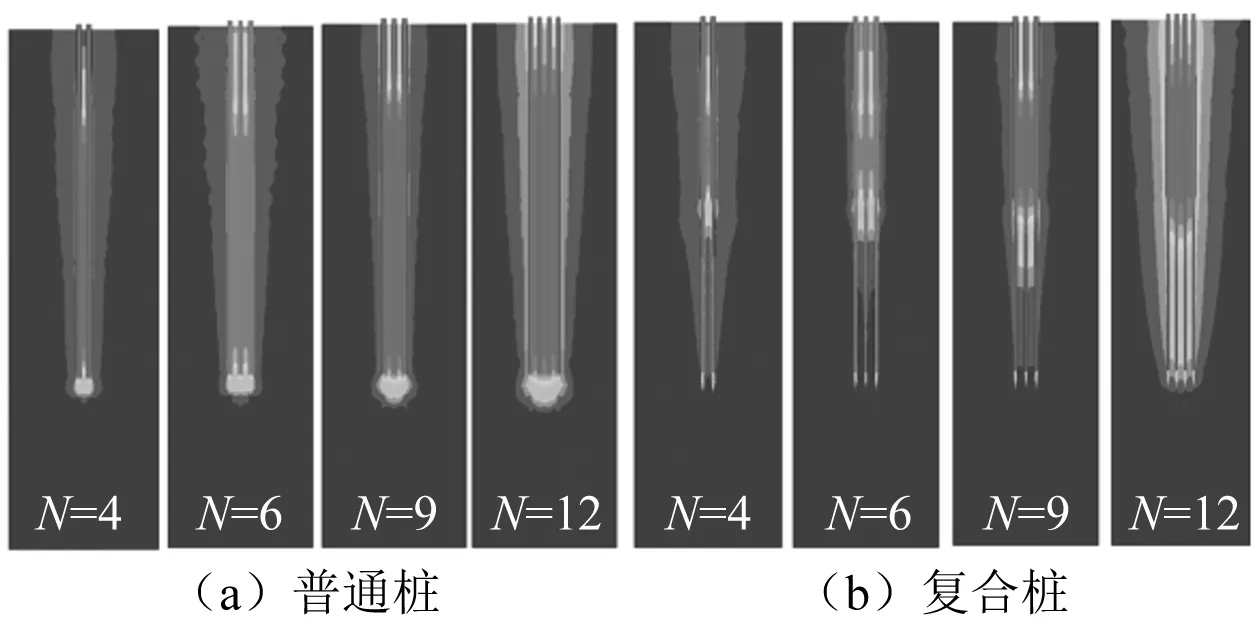
图13 不同N下群桩基础位移云图

当Sa/D1=2.0时普通钢管群桩基础均呈现整体破坏模式，基桩夹持作用随N的增大而加强，夹持作用区域从桩身中部区域向两端延伸。当Sa/D1=2.0时复合群桩基础均呈现非整体破坏模式，与普通钢管桩一样基桩夹持作用随N的增大而加强，夹持作用区域出现在上段桩身中部区域并向两端延伸，当N=12时夹持作用影响到下段桩。

图14为不同N下2种群桩基础角桩轴力分布规律。

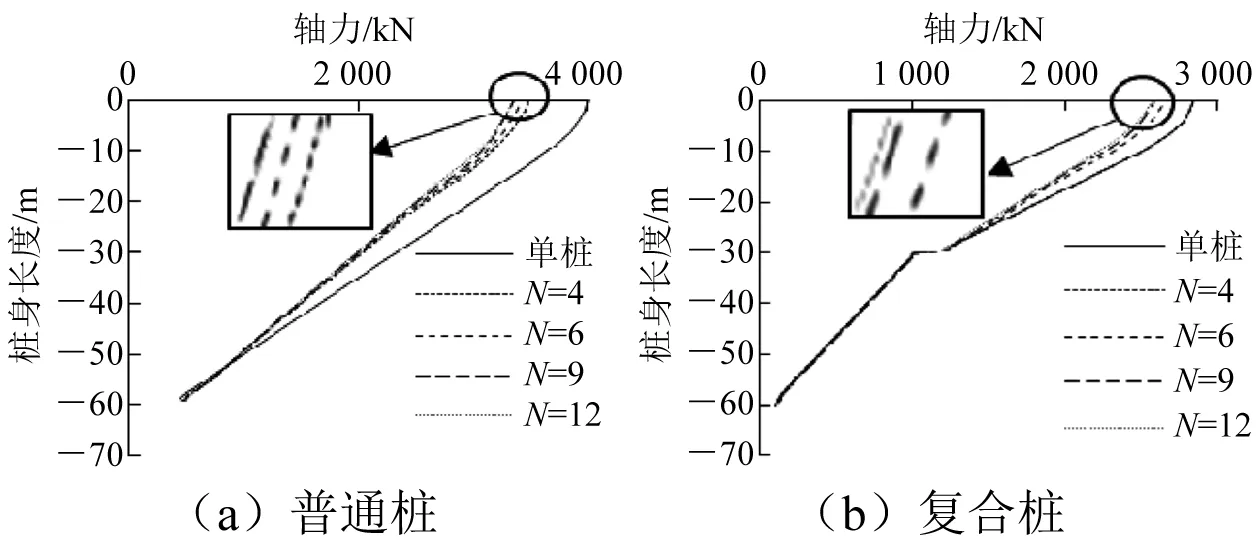
图14 不同N下角桩轴力分布

由图14可知：角桩桩顶轴力及变化规律相近，普通钢管群桩角桩与单桩桩顶轴力比约0.85，隔水导管复合群桩角桩与单桩桩顶轴力比约0.90；随着N的增大，侧摩阻力折减区域略有扩大，这与夹持作用区扩大有关，说明在不同N下角桩承载力的发挥对于群桩效应的影响较小。

除此之外，通过计算可得当N=9、12时，普通钢管群桩中心桩与单桩桩顶轴力比分别为0.40、0.33，隔水导管复合群桩中心桩与单桩桩顶轴力比分别为0.59、0.50，可知N的增大会减弱中心桩承载力的发挥。

2.4 桩径的影响

图15为1号～8 号计算模型在Sa/D1=2、N=9下基桩平均载荷位移曲线。在不同D1下2种群桩基础载荷位移变化规律相同，均随着D1的增大而增加。这是由于在桩长一定时，D1越大，桩侧表面积越大，侧摩阻力越大，基桩承受的载荷越多。在相同平均载荷下，D1越小沉降量越大。

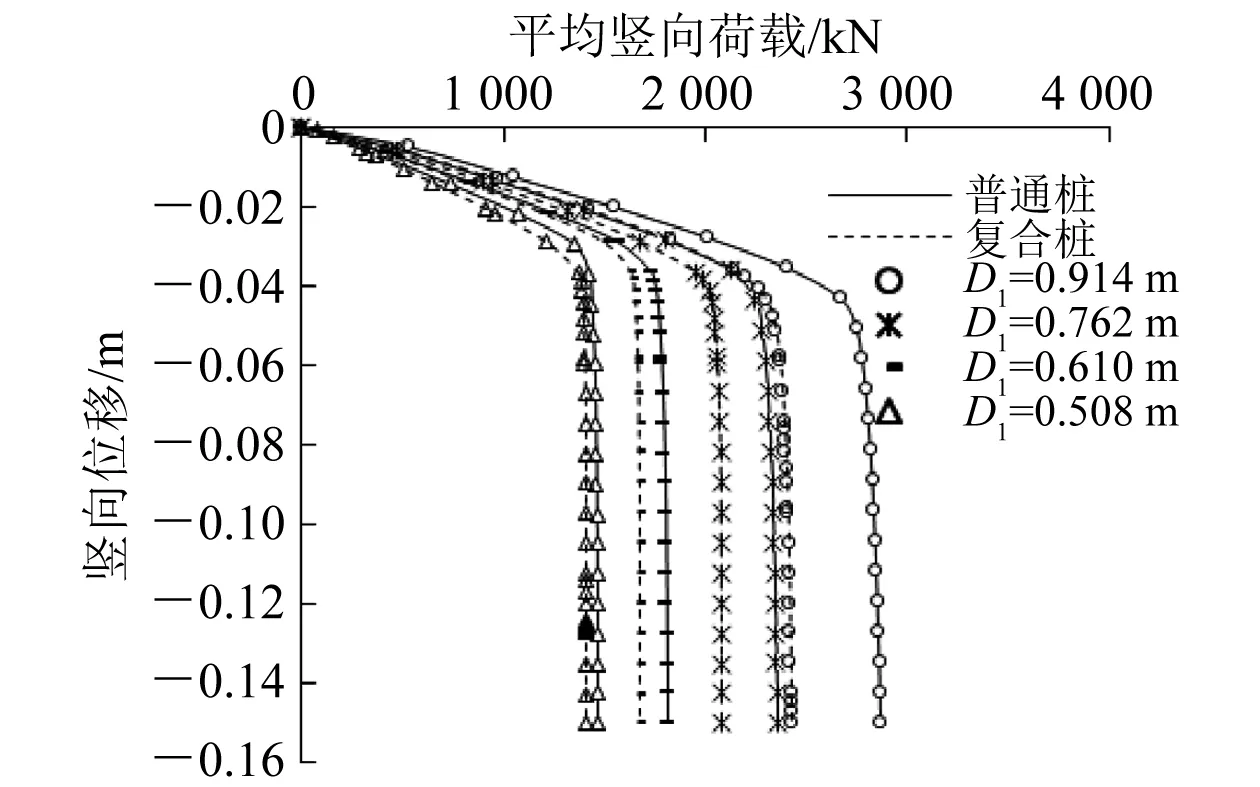
图15 不同D1下竖向载荷位移曲线

不同D1下2种群桩基础群桩效应系数结果如图16所示。

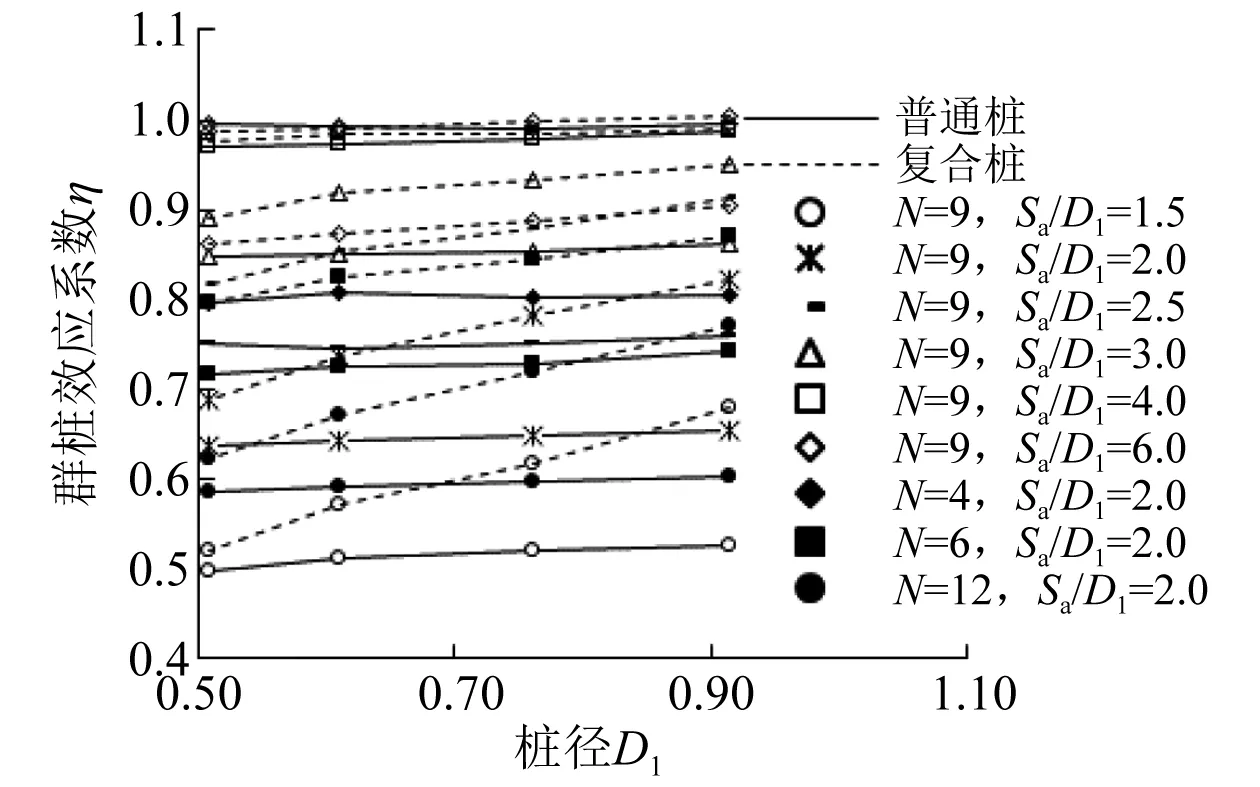
图16 不同D1下群桩效应系数曲线

由图16可知：普通钢管桩η对D1变化不敏感；隔水导管复合桩η在相同D2下随着D1的增大而逐渐增大，但随着Sa/D1的增大、N的减小，这种差距减小；在相同情况下，隔水导管复合桩的η大于普通钢管桩，但随着D1减小这种差距减小。

在不同D1下，2种群桩基础达到极限承载力时位移云图如图17所示。

图17 不同D1下群桩基础位移云图

由图17可知，当Sa/D1=2.0时普通钢管群桩基础均呈现整体破坏模式，基桩夹持作用随D1的减小而加强，桩端破坏模式也从局部剪切破坏向整体破坏过渡。与文献[14]得出结论一致，在Sa/D1不变的情况下，随着D1增大，基桩对桩间土的夹持影响强度减弱。当Sa/D1=2.0时隔水导管复合群桩基础1号、2号桩呈现非整体破坏模式，3号、4号桩呈现整体破坏模式。1号隔水导管复合群桩基桩夹持作用仅出现在上段桩，其余均延伸至下段桩，随D1减小夹持作用区域扩大，甚至导致破坏模式发生改变。

不同D1下中心桩轴力分布如图18所示。

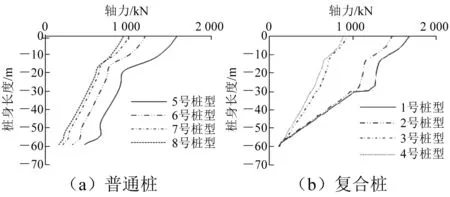
图18 不同D1下中心桩轴力分布

由图18可知：中心桩桩顶轴力随着D1的增大而增大；不同D1下普通钢管群桩和隔水导管复合群桩上段部分轴力减小速率相同，隔水导管复合群桩下段桩轴力减小速率在相同D2下随D1的增大而增大。桩身长度为0 m时桩身轴力即为桩顶轴力，可得普通钢管群桩模型在D1=0.914 m、0.762 m、0.610 m、0.508 m下中心桩与单桩桩顶轴力比值分别为0.40、0.37、0.38、0.40，隔水导管复合群桩分别为0.59、0.56、0.48、0.44。普通钢管桩群桩效应对D1变化不敏感，复合群桩对D1变化敏感，D1越小基桩夹持作用越强，效应越大。

2.5 桩长的影响

为研究不同下段桩桩长L2对群桩基础竖向承载力变化规律影响，保持桩径及其他参数不变，建立隔水导管复合桩不同桩型在L1=30 m，L2=20 m、30 m、40 m、50 m下的单桩及群桩模型，同时建立相同总桩长的普通钢管桩。通过计算得到不同桩型群桩基础在不同L2下的基桩平均载荷位移曲线，以5号和1号桩型为例，结果如图19所示。

由图19可知：在不同L2下2种群桩基础具有相同的载荷位移变化规律，群桩基础的平均极限承载力随着桩长的增加而增加；在相同上部竖向载荷作用下群桩位移随着桩长的增加而减小，且达到极限承载力时位移随桩长的增加而增加。

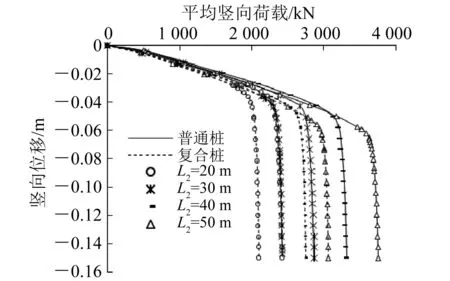
图19 不同L2下竖向载荷位移曲线

计算不同桩长下2种群桩基础群桩效应系数，所得结果如图20所示。

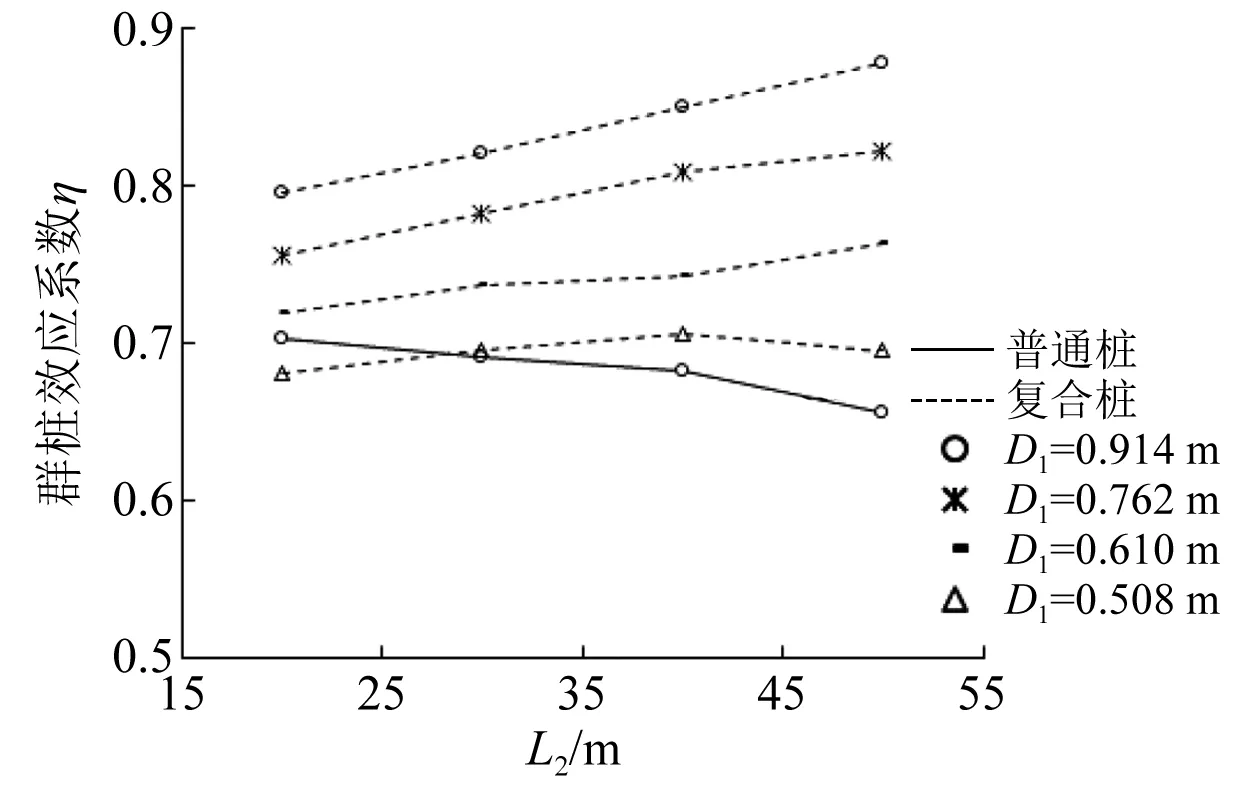
图20 不同桩长下群桩效应系数曲线

由图20可知，在不同桩长下2种群桩基础η变化规律相反。隔水导管复合桩η随L2的增加而增大，且在D1较大时改变L2对η影响较大，而D1较小时变化幅度较小。普通钢管桩η随桩长L的增加而减小。

选取不同桩长下2种群桩基础达到极限承载力时位移云图进行深入分析，以5号和1号桩型组成的群桩基础为例，如图21所示。

图21 不同桩长下群桩基础位移云图

由图21可知：当Sa/D1=2.0时普通钢管群桩基础在不同桩长L下均呈现整体破坏模式，基桩夹持作用随桩长L增加略有增强；当Sa/D1=2.0时隔水导管复合群桩基础在不同L2下均呈现非整体破坏模式，基桩夹持作用随桩长增加略有增强，但夹持作用区未延伸至下段桩。可见基桩侧摩阻力折减略有增大，但各基桩极限承载力增长幅度更大，从而承载力折减率降低，η增大，与图20所示规律相符。

图22所示为不同L2下中心桩桩身轴力分布规律。由图22可知，2种群桩基础在不同L2下中心桩桩顶轴力随桩长的增加而增大，各工况下中心桩桩身轴力变化规律基本相同。以5号和1号桩型为例：当隔水导管复合群桩基础L2=20 m、30 m、40 m、50 m时，单桩桩顶轴力分别为2 289.00 kN、2 622.19 kN、2 905.00 kN、3 225.00 kN，则可得中心桩与单桩桩顶轴力比分别为0.52、0.56、0.68、0.70；在相同总桩长下普通钢管群桩基础单桩桩顶轴力比分别为3 279.00 kN、4 090.00 kN、4 688.00 kN、5 367.00 kN，则可得中心桩与单桩桩顶轴力比分别为0.44、0.39、0.38、0.37。可见L2的增加会提高复合桩中心桩承载力发挥程度，但会降低普通桩中心桩承载力的发挥程度。

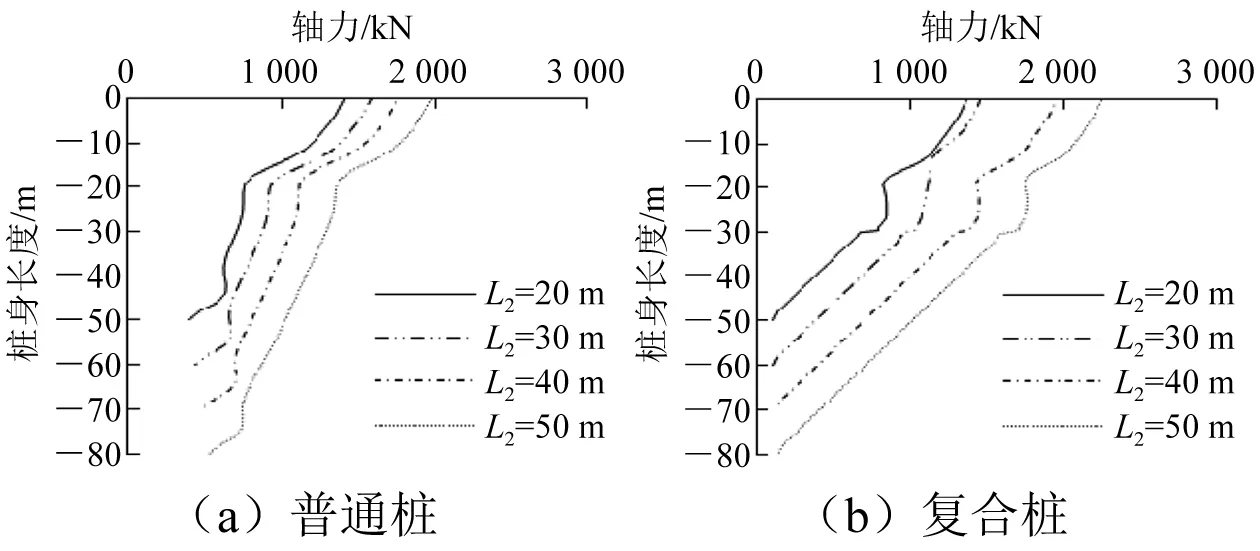
图22 不同L2下中心桩轴力分布

2.6 不排水强度的影响

1号～8号桩型在不同不排水强度Su下群桩效应系数如图23所示。

由图23可知，η随土体Su的增大而增大。在D1=914 mm和D1=762 mm工况下：当土体Su较小时，η对土体Su变化较为敏感，呈线性变化；当土体Su较大时，曲线较为平缓；当Su=80 kPa时，η为1，表明群桩效应消失。复合桩中在D1=610 mm工况下，η随土体Su变化一直呈线性变化，在Su=100 kPa时，η为1。在相同Su下，D1越小，群桩效应越明显，与第2.4节所得结论相符。

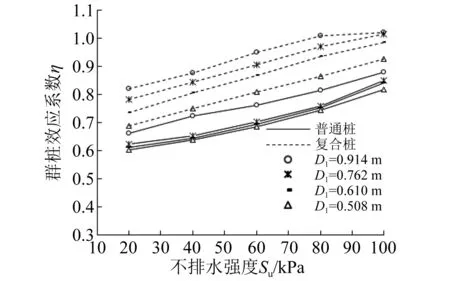
图23 不同Su下群桩效应系数曲线

3 隔水导管复合桩群桩效应系数公式

3.1 隔水导管复合桩的承载力折减率

在《水运工程地基设计规范》中黏性土群桩效应系数公式[12]为

(2)

式中：λ为平均承载力折减率；AS1、AS2、AS3分别为横、纵、斜向桩承载力折减率；m、n分别为横、纵向桩数。

在式(2)中承载力折减率AS以普通等截面钢管桩为研究对象，将其拓展应用于隔水导管复合桩，考虑变截面对承载力折减率的影响。隔水导管复合桩单桩地基应力分布如图24所示。

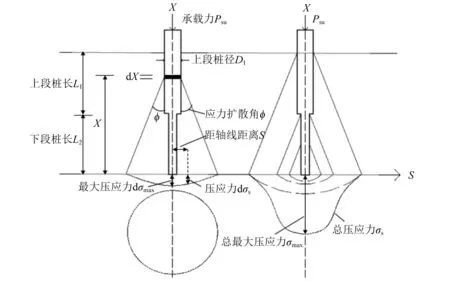
图24 复合桩单桩地基应力分布

在图24中桩侧摩阻力按照应力扩散角φ向下扩散，传至桩端平面处的压力呈抛物体形分布，桩端轴线处最大压应力为dσmax，距离轴线S处地基应力为dσs。假定黏性土中隔水导管复合桩为摩擦桩，桩外侧摩阻力沿桩身均匀分布，忽略变截面及端部处阻力，则作用在距桩端x处桩身微小段摩阻力dPsu为

(3)

式中：Psu为总承载力。

由于基础底面下所有压力之和在数值上与抛物体体积相等，且等于微小段上摩阻力，则可得抛物体体积为

dV=dPsu

(4)

由几何关系可得，抛物体体积近似等于外包圆柱体体积的一半[15]：

dV=

(5)

联立式(3)～式(5)可得：

(6)

由于桩端平面上dσs轮廓为对称分布的抛物曲线，则dσs表达式为

dσs=AS2+C

(7)

式中：S为距轴线距离；A为抛物线中参数S系数；C为抛物线常数项。

式(7)满足两个边界条件：

(8)

式中：D为计算点处桩的直径。

联立式(6)～式(8)可得：

(9)

对式(6)和式(9)进行积分得：

(10)

(11)

群桩基础应力互相重叠，两桩轴线之间距离S此时用Sa表示，即桩间距。其应力分布与单桩对比如图25所示。

由图25可知，当群桩基础桩间距小于临界距离时，侧摩阻力在扩散作用下互相重叠，致使桩端处土体所受极限承载压应力大于单桩，继而引发桩体产生过大沉降或刺入破坏。为减弱该效应，群桩中各桩平均承载力须小于单桩承载力，其折减率AS可用各桩传递的重叠应力σs与单桩桩端最大应力σmax的比值表示：

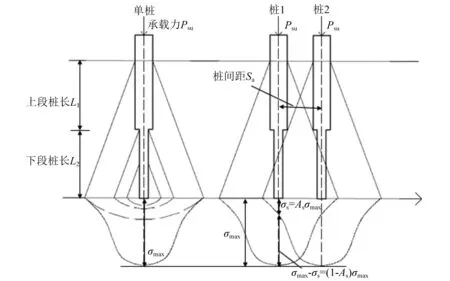
图25 复合桩群桩应力重叠图

(12)

联立式(10)～式(12)，可得：

(13)

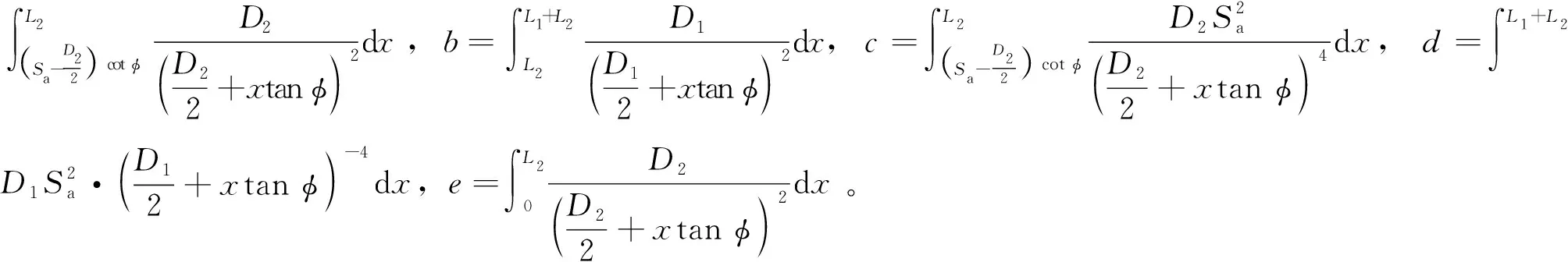
将横、纵、斜向桩间距Sa1、Sa2、Sa3分别代入式(13)中Sa即可得到式(2)中AS1、AS2、AS3横、纵、斜向桩承载力折减率。

3.2 隔水导管复合桩的群桩效应系数

由式(13)计算复合桩AS，代入式(2)求解η，并与有限元数值模拟所得η进行对比。其中以下2种工况不适用于式(2)：(1) 桩端阻力占比大于10%的工况；(2) 群桩破坏模式发生改变，例如Sa/D1=1.5时桩端产生整体破坏的工况。其余工况以Su=20 kPa为例，由公式所得η与有限元数值模拟所得结果进行对比，如图26所示。

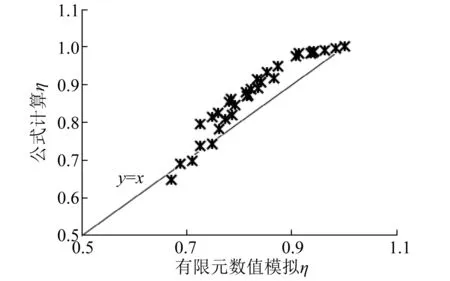
图26 有限元数值模拟与公式群桩效应系数对比

L1、L2、D1、D2、S、m、n按工况情况进行选取；根据文献[12]当土层强度较小时，应力扩散角较小，φ取6°；当AS计算值小于0时，AS取0。按照规范中普通钢管桩的群桩效应系数公式和本文公式分别计算不同桩数下5号普通桩和1号复合桩群桩效应系数，并将结果绘于图27。

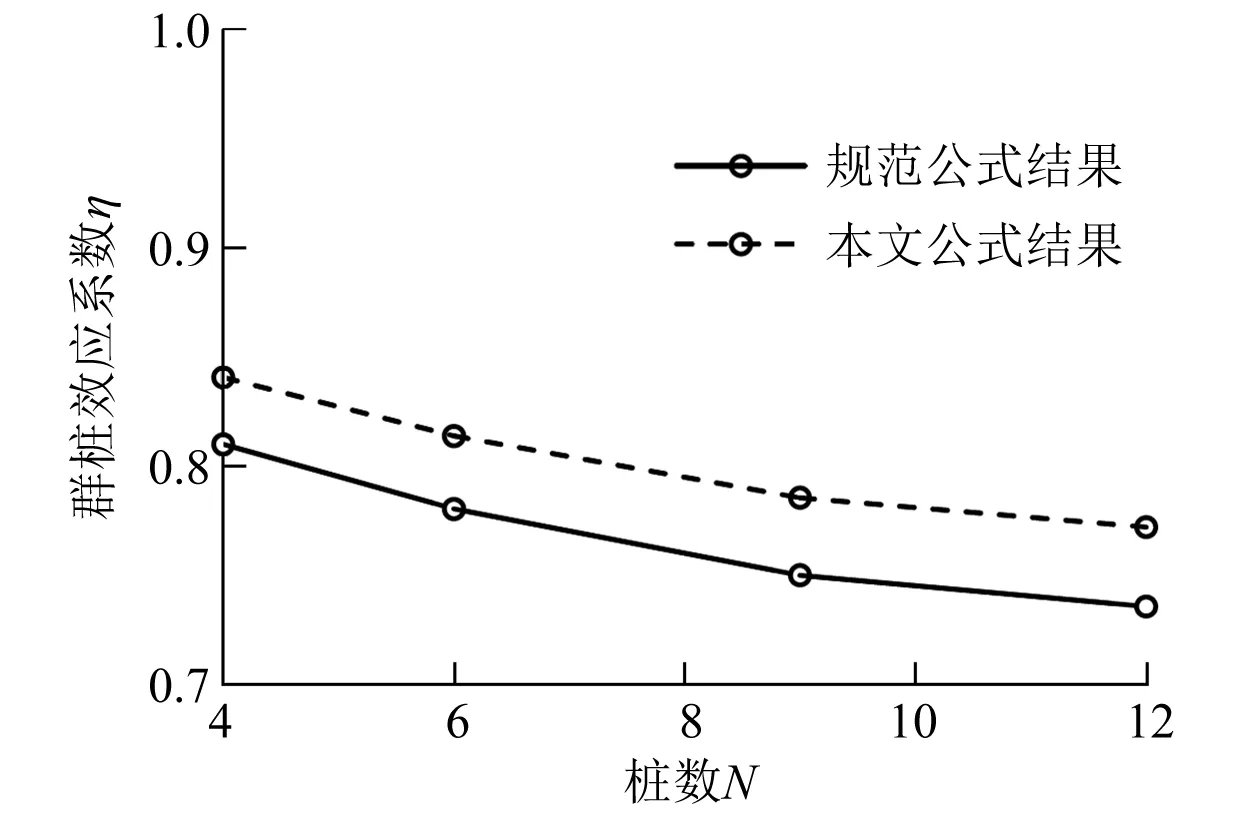
图27 两种公式计算η对比

由图26可知，式(13)所得η与有限元数值模拟所得η构成点分布在直线y=x附近，平均误差为6.756%，说明二者吻合良好。由图27可知，规范公式所得普通钢管桩和本文公式所得隔水导管复合桩的η均随着N增大而减小。在相同桩数情况下隔水导管复合桩η约为普通钢管桩η的1.2倍。

4 结 论

研究黏性土中隔水导管复合群桩基础竖向承载特性，主要结论如下：

(1) 隔水导管复合桩η随Sa/D1的增大、N的减小、D1的减小及Su的增大而增大。与普通钢管群桩基础相比，隔水导管复合桩η更高，但差距随着Sa/D1的增大、N的减小及D1的减小而减小。

(2) 隔水导管复合群桩基桩夹持作用、侧摩阻力折减幅度和范围随Sa/D1的减小、N的增大及D1的减小而增大，且主要发生在上段桩，少量涉及下段桩。与普通钢管群桩基础相比，隔水导管复合群桩中基桩的夹持作用相对较弱，破坏模式更接近非整体破坏模式，侧摩阻力发挥更加充分。

(3) 基于隔水导管复合桩存在明显变截面特点，利用应力叠加法对承载力折减率进行推导，得到适用于复合桩群桩效应系数计算公式，公式所得结果与有限元计算结果吻合良好。