深度强化学习算法在智能军事决策中的应用

况立群，李思远，冯 利，韩 燮，徐清宇

1.中北大学 大数据学院，太原 030051

2.北方自动控制技术研究所 仿真装备部，太原 030006

现代战争规模与复杂性不断扩大，作战方式日益复杂，面对瞬息万变的战场环境，仅靠人类决策行动已经很难确保正确快速的军事响应[1]。深度强化学习在解决序贯决策问题上做出了许多突出贡献，契合了指挥员的经验学习与决策思维方式，二者相结合是现代智能军事决策的发展方向。强化学习[2]具有鲁棒性强[3]、独立于环境模型和先验知识等优点，在运用于军事作战行动中常采用试错法寻求最优军事决策序列。Q-Learning[4]是一种典型的强化学习方法，已被广泛地研究并产生了SARSA[5]、深度Q网络（DQN）[6]、Double-DQN[7]等改进算法。Q-Learning被大量应用于军事决策中的部分环节中，如战机路径规划[8]以及半自治坦克军事决策[9]。2015年，DeepMind团队提出了DQN算法，将深度卷积神经网络和Q学习结合到一起，在Atari系列游戏上达到了人类专家[10]的决策和控制水平，并且避免了Q表的巨大存储空间；此外还利用经验回放记忆和目标网络提高了训练过程的稳定性。陆军工程大学依据该算法提出了一种基于DQN的逆向强化学习的陆军分队战术决策技术框架[11]，在解决战术行动决策上取得了一定的效果。

虽然DQN算法在离散行为决策方面取得了一系列成果[12]，但是难以实现高维的连续动作。如果连续变化的动作被无限分割，那么动作数量会随着自由度的增加而成倍增加，这就导致了维度突变的问题，网络将难以收敛。常见做法是对真实的作战系统进行有限的网格化处理，形成若干离散的空间与动作，其弊端是大大降低了真实作战环境的复杂性，丢失了很多环境与动作细节。例如，在人员移动方面只能产生离散的运动，难以准确地模拟真实战场环境下的人员决策行为[13]。

2015年，Lillicrap等人[14]综合DQN算法、经验回放缓冲区和目标网络的优点，提出了深度确定策略梯度（DDPG）算法来解决连续状态行为空间中的深度强化学习问题。同时，采用基于确定性策略梯度的演员-评论家（Actor-Critic）算法使网络输出结果具有确定的动作值，保证了DDPG可以应用于连续动作空间领域[15]，弥补了DQN算法无法适用于连续动作空间的缺点。然而，由于DDPG算法中Actor网络和Q函数之间的相互作用，使得算法通常难以达到稳定，因此很难直接将DDPG算法应用到复杂的高维多智能体环境。在多智能体环境下，各个智能体之间会产生相互影响和制约[16]，引起环境的变化，导致算法难以收敛。陈亮等人[17]在DDPG算法的基础上提出了一种改进DDPG的多智能体强化学习算法，该算法虽然构建了一个允许任意数量智能体的灵活框架，但由于所有智能体共享当前环境的相同状态，使得环境状态维数增加，且环境会受到所有智能体策略动作的影响，导致算法收敛比较困难。赵毓等人[18]在多智能体环境下的无人机避碰计算制导方法中通过采用集中训练-分布执行来满足多智能体算法稳定收敛的要求，但是该算法只能局限于少量智能体参与，无法满足任意数量智能体的策略学习。

综上，为解决深度强化学习算法难以运用于高度复杂且连续决策的现代战场环境，同时多智能体环境下算法难以收敛的问题，本文提出了一个改进的DDPG算法——单训练模式双噪声DDPG算法（Single-mode and Double-noise DDPG，SD-DDPG），在经验采样、奖励函数[19]、探索策略[20]和多智能体框架[21]方面对DDPG算法进行改进。基于优先级的经验重放技术[22]更加注重有价值经验的学习，提高算法的收敛速度；连续型奖励函数突破稀疏奖励长时间无法变化的困境；OU噪声与高斯噪声相结合的智能体探索策略，满足连续决策与离散决策的探索要求；多智能体框架为每个作战单位分配单独的深度强化学习算法，采用单模式训练策略来大大提高算法收敛的速率和稳定性。

1 相关工作

DDPG是深度强化学习中一种可以用来解决连续动作空间问题的典型算法，可以根据学习到的策略直接输出动作。确定性的目的是帮助策略梯度避免随机选择，并输出特定的动作值。目前，DDPG算法在无人驾驶汽车和无人驾驶船舶领域有着较为成熟的应用，由于DDPG算法有着很强的序贯决策能力，恰好与军事决策思维方式有很大的契合，因此将其应用在智能军事决策领域具有重要价值。图1为DDPG算法框架。

图1 DDPG算法框图Fig.1 DDPG algorithm block diagram

DDPG算法以初始状态信息S t为输入，输出结果为算法计算出的动作策略μ(S t)。在动作策略中加入随机噪声，得到最终的输出动作，这是一种典型的端到端学习模式。在启动任务时，智能体（agent）根据当前状态s t输出一个动作，设计奖励函数并对该动作进行评价，以验证输出动作的有效性，从而获得环境的反馈奖赏r t。有利于agent实现目标的行为将得到积极奖励，相反，给予消极惩罚。然后，将当前状态信息、动作、奖励和下一次的状态信息(s t,a t,rt,s t+1)存储在经验缓冲池中。同时，神经网络通过从经验缓冲池中随机抽取样本数据，训练经验，不断调整动作策略，更新网络参数，进一步提高算法的稳定性和准确性。

DDPG是较为先进的深度强化学习算法，具有处理高维连续动作空间的能力，然而DDPG算法中Actor网络和Q函数之间的相互作用使得算法通常难以达到稳定，且超参数的选择也变得非常困难，因此难以直接将DDPG算法应用于军事决策下的多智能体环境。

2 军事决策环境状态定义

2.1 仿真平台设计

军事决策领域涵盖内容非常广泛，本文选取了蓝军步兵进攻红军军事基地这一具体军事作战行动。基于Unity独立开发了智能军事决策仿真训练环境，将蓝军步兵进攻红军军事基地作战行动映射到基于Unity的模拟环境中去，实现了作战智能体在模拟环境下进行军事决策行为的训练学习。

为了更加高效地探究基于深度强化学习的智能军事决策能力，本文对蓝军步兵进攻红军基地军事行动定义如下规则。基于Unity搭建1 000 m×1 000 m作战环境，预设6名蓝军步兵作为一个小队进攻红军基地，作战智能体可以在360°范围内进行移动与射击操作，作战智能体的个数在仿真环境接口中进行设定。在该模拟环境中预先设置多个障碍物，作为红军军事基地的保护屏障，作战智能体无法自由穿过障碍物，红军军事基地坐落在障碍物后方。该军事作战模拟环境具有高度的自由性，障碍物的数量、位置以及基地的大小位置都可以自由设定，模拟环境中还搭建了山体、树木、草地等易于作战智能体隐蔽的区域，更加符合真实的作战场景，满足多种军事作战行动环境的要求。具体模拟环境如图2所示。

图2 模拟作战环境Fig.2 Simulation environment

2.2 环境状态数据提取

蓝军步兵进攻红军基地军事作战行动中的环境状态信息涉及作战智能体的位置信息、动作信息、障碍物及基地信息等。本文改进的DDPG算法中使用的环境状态信息如表1所示。

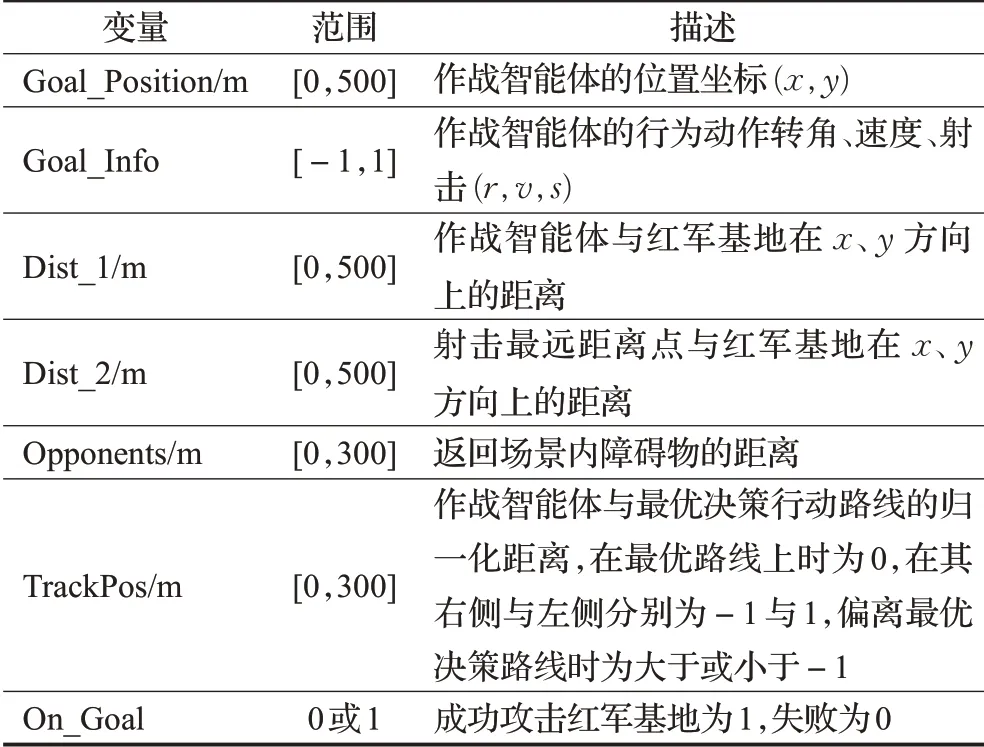
表1 输入变量定义Table 1 Input variable definition

在真实的蓝军步兵进攻红军基地军事行动中，作战人员会依据环境的特点选取一条最优的行动路线，模拟环境中将作战智能体与最优决策路线的距离归一化为

[-1,1]，距离越小表明学习到的策略越好。

由于作战智能体获得的是多个不同类型的环境状态数据，信息具有多样性与复杂性，因此需要进行有效融合与处理，作为环境的状态输入。具体操作为：

（1）收集所有不同类型的具有价值的环境状态数据。

（2）对收集到的环境状态数据进行分析，筛选特征值，剔除不合理的数据，合并具有共同描述特征的数据。

（3）归一化处理状态特征值，便于神经网络的处理与学习。

（4）对经处理后不同目标的状态值进行组合，设置为Numpy中ndarray对象格式，作为输入状态。

2.3 作战规则约束

在真实战场环境下，蓝军步兵进攻红军军事基地，为保证蓝军步兵的隐蔽性，在距离红军军事基地较远距离时（直线距离大于200 m），不得执行射击动作。战场环境中，军事障碍物不可穿越，蓝军作战单位应当绕过障碍物，占据优势位置后对红军基地发动攻击。为保证军事决策模拟的真实性，作战单位执行射击操作有射程限制，该军事行动中限制为200 m。

2.4 输出动作控制

作战智能体具有高度的灵活性，可以全方位自由运动与射击，解决了传统智能军事决策算法只能执行一定离散动作的问题，极大提高了军事决策模拟的真实性。同时，这也涉及到更为精确的动作控制，包括作战智能体的运动方向、运动速度、射击操作。变量定义如表2所示。

表2 输出动作变量定义Table 2 Output action variable definition

3 奖励设计

DDPG算法采用连续的动作空间，一个任务回合内需要采取的动作空间很大，离散的奖励函数在一定的动作范围内只能给出相同的奖励值，无法对动作的细微变化进行精确有效的评价，使得模型难以收敛。

针对以上问题，本文设计了具有持续奖励支持的连续性奖励函数。奖励函数如公式（1）所示：

式（1）中，(x,y)是作战智能体的位置坐标，r是方向弧度值。当作战智能体越过环境边界或者与障碍物相撞时，奖励值设置为-200，给予惩罚。当作战智能体执行射击动作但未击中目标，则累加奖励值-100。为了引导作战智能体更快地学习到最优军事决策策略，设计连续性函数引导作战智能体到达预先设立的区域，距离值越小获得的奖励值越大。到达指定区域附近后，将射击点与红军基地的距离设为奖励函数，引导作战智能体向红军基地位置进行射击。持续性的奖励刺激可以更加高效地引导智能体快速学习到最优决策序列。该作战任务的最终目标是将红军基地摧毁，给予奖励值+200。

4 SD-DDPG算法

本文提出一个改进的DDPG算法——单模式训练双噪声DDPG算法（Single-mode and Double-noise DDPG，SD-DDPG），该算法构建一个允许任意数量agent的灵活框架，所有agent共享当前环境的相同状态空间，且每个作战agent具有相同的动作空间，采用基于优先级的经验重放技术和混合双噪声，以及增加单训练模式来改进DDPG算法。SD-DDPG算法对比DDPG算法在智能军事决策模拟环境中有更快的收敛性和更高的稳定性。

4.1 基于优先级的经验重放技术

原始的DDPG算法引入了经验重放机制，使用经验重放缓冲区消除输入经验中存在的相关性，然而，该经验重放机制基于存储在重放缓冲区中的所有经验都具有同等重要性的设定，因此随机地对一小批经验进行采样来更新网络。这种设定有违常理，当人们学会做某事时，获得巨大回报的经验和非常成功的尝试或惨痛的教训会在学习的过程中不断地出现在他们的记忆中，因此这些经验更有价值。

在大多数强化学习算法中，TD-error经常被用来矫正Q(s,a)函数。TD-error的值作为估计值的修正值反映了agent可以从中学习到正确策略的程度。TD-error的值越大，表明对期望动作值的修正越积极，在这种情况下高TD-error的经验更有可能具有更高的价值，并且与非常成功的尝试紧密联系。此外，TD-error为负的情况与非常失败的尝试紧密联系，通过对非常失败经验的学习可以逐步使agent避免再做出错误的行为，这些不好的经验同样具有很高的价值。选取TD-error作为评价经验价值的标准，对经验j计算TD-error如公式（2）所示：

式中，Q′(s t+1,a t+1,w)是w参数化的critic目标网络。抽样经验的概率定义如公式（3）所示：

式中，P(j)表示对经验j进行抽样的概率，其中D j=表示第j个经验在经验缓冲池中的位置排序。参数α决定了优先级的使用程度，抽样概率的定义可以被视为在经验选择过程中加入随机因素的方法，这可以使得TD-error值比较低的样本仍然有机会被重放，从而保证了经验抽样的多样性，防止神经网络过度拟合。但是由于对具有高TD-error经验的频繁重放，无疑改变了样本的分布，这很可能导致模型收敛到不同的值或者训练不收敛，所以需要选择重要性采样，这样可以确保每个样本被选到的概率是不同的，且对梯度下降具有相同的影响。重要性采样权重如公式（4）所示：

式中，S是经验缓冲池的大小，P(j)是采样经验j的概率，β是一个超参数，用来控制基于优先级经验缓冲池重放程度，如果β=1，代表完全抵消优先级经验缓冲池对收敛结果的影响。

4.2 基于混合双噪声的探索策略

DDPG算法中添加噪声的动作策略与学习策略相互独立，即DDPG是确定性策略，而探索噪声可以自行设定。

原始DDPG算法采用OU（Ornstein-Uhlenbeck）噪声，OU过程是一种随机过程，其微分形式如公式（5）所示：

其中，μ是均值，θ表示噪声趋于平均值的速度，σ表示噪声的波动程度。OU噪声是时序相关的探索噪声，即前一步的噪声会对后一步的噪声产生影响，且是马尔科夫模式的。正是基于OU噪声时序相关的特性，对于惯性系统的探索效率会更高。而DDPG作为连续性算法的代表，非常适用于惯性系统。

许多强化学习算法也经常采用高斯噪声，将强化学习算法中策略网络的输出动作作为均值，直接叠加高斯分布ε～Ν(0,σ2)，作为强化学习算法的探索策略。区别于OU噪声时序相关性，高斯噪声不会受到之前动作的影响，所以对于不具备时序相关的决策动作非常适用于高斯噪声。

在基于改进DDPG算法的蓝军步兵进攻红军军事基地智能决策行动中，作战智能体具有三个决策动作，其中速度与方向的控制适用于惯性系统，采用OU噪声可以提高作战智能体在速度控制与方向选择策略的探索效率，但是针对作战智能体的射击动作，由于射击动作的执行在时序上不具备相关性，即前一步的射击动作不会对后一步是否采取射击动作产生影响，因此采用OU噪声则会降低射击决策动作的探索效率。由于高斯噪声具有独立噪声的特点，所以在射击决策上采用高斯噪声无疑是最好的选择。所以本文引入了OU+Gaussian的混合双噪声来改进DDPG算法，提高算法在军事模拟环境中的探索效率和收敛速度。后续实验结果表明，采用混合双噪声的改进DDPG算法具有更快的收敛速度和更高的稳定性。OU噪声参数设定如表3所示。

表3 OU噪声参数设定表Table 3 OU noise parameter setting table

表3中，μ代表噪声的平均值，θ代表趋于平均值的速度，σ为噪声的波动程度。

4.3 增加单训练模式下的多智能体框架

直接将DDPG算法应用于具有多智能体的军事决策环境中，算法将很难收敛，因此本文设计了增加单模式下的多智能体灵活框架。在本文设计的多智能体框架中，每个作战智能体独立分配一个改进型DDPG算法，每个作战智能体拥有独立的神经网络和基于优先级的经验缓冲池。每个作战智能体在与环境的交互中，接收全局的环境状态信息，即将全局环境状态作为Actor网络的输入，Critic网络则独立地对本智能体决策动作进行评价和训练。

由于环境中同时存在多个作战智能体，且依据时间步循环对每一个作战智能体进行训练，这会导致环境的动态变化，降低了算法的收敛速率和稳定性，使算法难以收敛。针对以上问题，本文提出了增加单模式下的多智能体框架。即在多智能体框架中加入单模式控制模块，对每一个作战智能体在特定时间步内增加单训练模式。单训练模式下，算法指定的单作战智能体独立地与环境交互，学习决策策略，其他作战智能体临时进入休眠状态，不会对环境产生影响。退出单训练模式，则多个智能体同时对环境进行探索，学习多智能体协作策略。增加了单模式的多智能体框架，可以大幅提高算法收敛的稳定性和速率，既保证了多智能体间可以学习到一定的协作策略，又可以使每个作战智能体具有一定的独立性。

在蓝军步兵进攻红军基地智能决策行动中，SDDDPG算法可以稳定且高效的收敛。SD-DDPG框架结构如图3所示。

图3 SD-DDPG框架图Fig.3 SD-DDPG frame diagram

5 实验结果与仿真

本文采用自主研发的基于Unity的智能军事决策模拟环境作为训练平台，该平台具有高度的仿真性和灵活性，采用三维模式构建，定义了一些通用的接口，通过这些接口可以自由设定满足特定军事任务的仿真环境，并且大部分经典算法都可以在该环境中进行测试。深度强化学习中，将累计奖励值作为评价深度强化学习算法收敛性与稳定的标准。

5.1 连续性智能军事决策

目前很少有研究将DDPG算法应用于智能军事决策领域。由于DDPG具有强化的深度神经网络函数拟合能力和较好的广义学习能力，且其决策动作空间具有连续性特点。本文选择DDPG算法作为智能军事决策的基础算法。

DQN算法在离散行为方面取得了很大的成功，但是很难实现高维的连续动作。此外，如果简单地将操作离散化会过滤掉有关操作域结构的重要信息，所以离散型的强化学习算法无法用于更为精确的模拟智能军事决策行为。图4是DQN算法在智能军事决策模拟图。

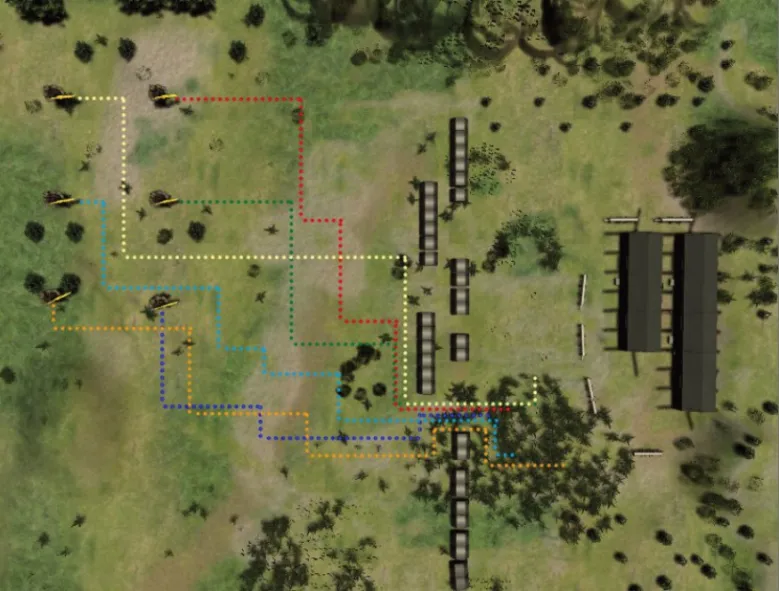
图4 应用DQN的离散军事决策模拟图Fig.4 Discrete military decision simulation chart based on DQN

DQN算法在蓝军步兵进攻红军基地军事决策中，只能输入离散的动作来适应网格化的地图环境，虽然算法得到了收敛，但是网格化的地图环境以及离散的动作控制大大降低了军事决策模拟难度，忽略了真实军事环境下作战单位执行动作的高维性。基于DDPG算法的改进算法则可以依据更强大的神经网络以及连续的动作控制，更加真实的对蓝军步兵智能军事决策行为进行模拟，图5是基于SD-DDPG算法的连续型军事决策模拟图。

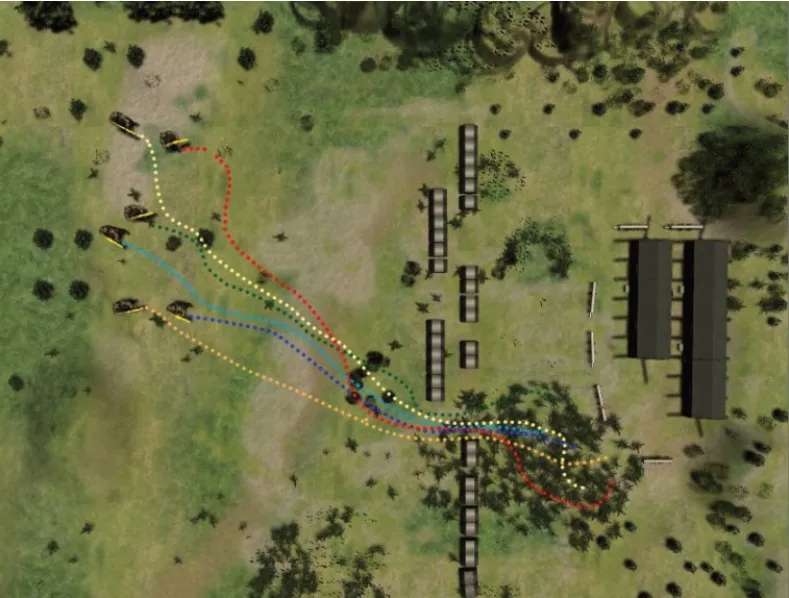
图5 基于SD-DDPG算法的连续型军事决策模拟图Fig.5 Continuous military decision simulation chart based on SD-DDPG algorithm

实验结果表明，基于SD-DDPG算法的智能军事决策能够稳定且高效地执行连续型动作控制，每个作战智能体在连续型奖励函数的引导下，快速且稳定地绕过军事障碍物到达指定隐蔽区域，之后智能执行射击动作，进攻红军军事基地，快速完成蓝军步兵进攻红军军事基地作战任务。对比离散型DQN算法，SD-DDPG算法应用于智能军事决策行为更具真实性与高效性，克服了目前在军事决策领域只能网格化作战环境与执行简单离散动作的弊端，是连续性动作控制在智能军事决策领域的一次全新尝试，为后续探索智能军事决策领域提供了全新的视野与方法。

5.2 SD-DDPG算法的性能测试

SD-DDPG算法是DDPG算法的改进算法，通过引入基于优先级的经验重放技术，解决了原始经验缓冲池中所有经验都具有同等重要性的弊端，通过加入OU与Gaussian混合双噪声来提高算法的探索能力，最后在多智能体框架下增加单训练模式，提高了多智能体与环境交互的稳定性，使算法能够快速且高效地收敛。

以DDPG算法作为基准算法，加入OU+Gaussian混合双噪声后，使决策动作的探索更加高效，算法收敛的稳定性有一定程度的提高。

图6在不同噪声环境下通过迭代训练300回合（episode）进行对比，每个回合最大训练次数为5 000次。实验结果表明，对速度控制和方向控制叠加OU噪声，以及对射击动作控制叠加Gaussian噪声后，DDPG算法在该军事决策模拟环境下具有更高的稳定性。

图6 OU噪声与OU+Gaussian混合噪声的奖励对比Fig.6 Comparison of OU noise and OU+Gaussian mixed noise

针对多智能体框架下，由于环境的动态变化而导致的算法不稳定且难以收敛的问题，本文增加了单训练模式，图7表示了增加单模式下的DDPG（Single-mode DDPG，S-DDPG）算法收敛速度与收敛稳定性都明显提升。

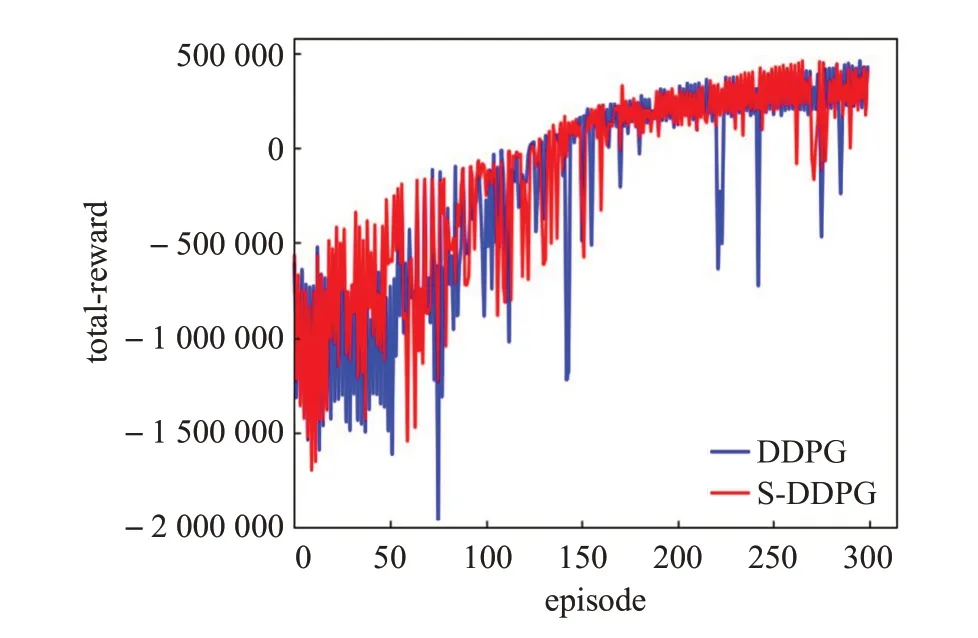
图7 增加单模式下DDPG算法与原始算法奖励对比Fig.7 Comparison of DDPG algorithm and original algorithm in single-mode

为最终验证SD-DDPG算法的先进性，本文选取Actor-Critic（演员-评论家）[23]、DDPG、PER-DDPG（基于优先级经验重放技术的DDPG）[22]等3种连续性深度强化学习算法与之比较，结果如图8所示。

图8 SD-DDPG算法与其他算法奖励对比Fig.8 Comparison between SD-DDPG algorithm and other algorithms

Actor-Critic算法由actor网络和critic网络两部分构成，可以执行连续的控制操作，也是DDPG算法的基本框架。PER-DDPG算法对原始算法进行了改进，使其具备了优先级的经验回放，能够更加高效地从经验中学习策略。图8中对比结果表明，本文采取的SD-DDPG算法比其他连续性算法具有更高的回合奖励和更快的收敛稳定性。

综上所述，在蓝军步兵进攻红军军事基地智能军事决策环境中，设定的6名作战智能体在SD-DDPG算法的指挥控制下，能够自主规划最佳路径，且在合适的时机下对红军基地实施火力打击，以最快的速度完美地完成了作战任务。SD-DDPG算法的超参数设置如表4所示。

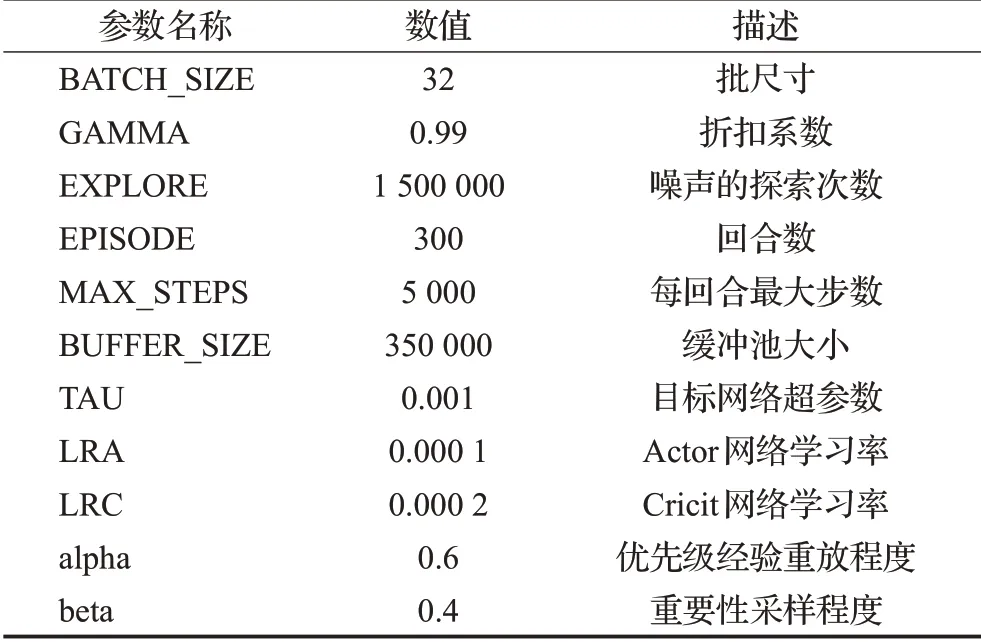
表4 SD-DDPG算法超参数Table 4 Super parameter of SD-DDPG algorithm

表4中超参数数值的选择依据反复实验与经验所得。批尺寸的大小一般为8、16、32、64等，大的批尺寸能够使模型更准确地朝着极值所在的方向更新，但批尺寸的选择也会受到计算机内存大小的限制，通过实验并结合计算机硬件实际条件，选择批尺寸大小为32。折扣系数反映了对未来奖励的期望程度，蓝军步兵进攻红军基地军事行动更关注于最终的战果，因此设置折扣系数为0.99。图7中算法在150个回合后趋于稳定，图6与图8表明算法在250个回合后趋于稳定，因此选择回合数为300以及每回合最大步数为5 000可以保证算法在最短时间内收敛，且不会因为过多的回合训练造成过拟合现象。噪声的探索次数根据回合数与每回合最大步数得出。经验缓冲池存储供网络训练的样本数据，过小的缓冲池必然会使一部分经验被丢弃，而过大的缓冲池又会受到计算机内存与性能的限制，通过多次实验，选择缓冲池大小为350 000。SD-DDPG算法通过软更新来更新目标网络参数，通常设定目标网络超参数为0.001。alpha与beta参数分别控制优先级经验重放程度与重要性采样程度，通过权衡攻击性与鲁棒性[24]，确定alpha与beta的数值为0.6与0.4。

学习率的选择是所有超参数调整中最为重要的，它会对模型的收敛性与学习速率产生重要影响。LRA与LRC的选择通常为0.01、0.001、0.000 1等。选择较大学习率可能导致模型不收敛，而选择较小学习率虽然会提高模型收敛的概率，但会影响模型的收敛速度。SD-DDPG算法中，critic网络对actor网络进行评价，通常需要更快的学习率。图9表明，学习率参数选择0.001数量级时，模型难以收敛，而LRA与LRC分别为0.000 1与0.000 2具有更快的收敛速度与稳定性。

图9 学习率参数对模型性能影响Fig.9 Influence of learning rate parameters on model performance

6 结语

本文以DDPG算法为基础，提出了SD-DDPG算法并应用于解决智能军事决策问题。通过引入基于优先级的经验重放技术、混合双噪声以及增加单训练模式来提高算法在军事决策问题上的收敛稳定性和收敛速度，是连续性军事决策智能生成的一次成功探索。实验结果表明，SD-DDPG算法具有更高的回合奖励、更快的收敛速度和更好的稳定性，可以有效地提升智能军事决策效率。但SD-DDPG算法弱化了多智能体间的交流协作，只能实现一定程度的交流协作能力，它更注重任务的快速完成。下一步将拓展研究范围，加强对以多智能体之间的通信为基础的多agent算法研究。