地下局部角度域高斯束偏移成像

黎孝璋 胡 林 任 婷 李 芳 鲁统祥

(中海石油(中国)有限公司海南分公司 海南海口 570312)

为了解决复杂介质高精度成像问题，地震偏移方法发展经历了从叠前时间偏移到叠前深度偏移[1-2]、从射线类偏移到波动方程偏移[3-5]、从常规偏移到基于迭代反演的最小二乘偏移[6-7]。相较于常规射线类偏移方法，波动方程偏移技术对于复杂构造成像质量有了较大提高，但是面对海量实际地震数据，当前计算机的计算能力还难以满足大规模工业化地震处理需求，基于射线理论的常规偏移技术依然是工业化生产的主流选择。受限于射线高频近似假设，常规射线类偏移技术对复杂构造成像存在局限，如何提高射线类偏移技术对复杂构造的成像精度一直是业界的重要研究方向。针对常规克希霍夫偏移无法适用于复杂构造射线多路径问题，人们发展了高斯束偏移技术[8-10]。高斯束偏移不仅仅解决了射线多路径问题，较大程度提高了成像精度，最重要的是还保留了积分法偏移高计算效率的优势，这点对于实际数据处理非常关键。但是在复杂构造情况下，无论哪种射线偏移技术，地面偏移距域射线偏移技术都会在偏移结果中产生运动学和动力学假象[11]，即使速度准确，偏移距道集同相轴也并非拉平[12]。

针对上述问题，很多学者提出了地下共成像点角度域射线偏移技术[13-15]，在偏移过程中生成地下成像点角度域道集，而不是传统射线偏移生成的偏移距道集。由于理论上反射系数为入射角的函数，而不是偏移距的函数，二者只有在简单层状介质情况下存在简单的函数关系，此外，地下局部角度域道集具有射线多路径自适应性，是唯一不存在假象的地震道集[16]，因此地下成像点角度域道集更加适用于AVA分析及叠前反演。Xu等人[17]系统分析了地下共成像点角度域偏移对复杂构造成像的优势，并且从理论上指明了地面共炮域或者共偏移距域偏移不满足成像条件的情况，而对于地下共成像点角度域偏移，绝大多数情况下反射波都满足成像条件，因此偏移成像假象可以较好地被消除。

综合上述偏移方法的优缺点，本文研究了一种地下局部角度域高斯束偏移方法，该方法具有计算效率高、成像精度高以及道集保幅性高的特点，有效解决了复杂构造成像多路径以及真反射角偏移成像问题。具体实现主要包括三个步骤：首先进行地下成像点的射线追踪及走时计算；然后求取地下成像点的局部反射角以在成像过程中对地震波场进行角度域映射；最后应用成像条件对数据进行角度域射线束偏移成像。

1 高斯射线束偏移

炮域高斯束叠前深度偏移主要包括以下步骤：首先利用高斯束积分理论计算地下震源波场；然后进行倾斜叠加，将地震记录分解为不同射线方向的波场；最后利用高斯束积分理论将地震记录反向延拓并应用成像条件进行成像。

二维介质高斯束偏移通过高斯束积分求取格林函数，震源坐标为xs的地下任意一点x点波前高斯束积分表达式为

(1)

式(1)中：ω为角频率；px与pz分别为震源入射射线初始慢度水平与垂直分量;uGB为入射高斯波束。利用动力学射线追踪计算高斯束的复值振幅A和走时T，上式可以表示为

(2)

高斯束是将波动理论和射线理论结合起来的方法，同时进行运动学和动力学射线追踪，然后根据所求的运动学和动力学参数计算介质任一点处的振幅和走时，最后将每条高斯束的有效波束叠加起来得到地震波前。

地面地震记录反向延拓公式为

U(x,xs,ω)=

(3)

式(3)中：U(x,xs,ω)为反向延拓的波场;θr为地下成像点x到接收点xr处的射线出射角；vr为接收点处的速度;“*”代表复共轭;u(xr,xs,ω)表示检波器及震源分别为xr、xs处的地震记录。结合式(1)，同时引入一个相位校正因子，考虑接收点附近高斯束反向延拓公式为

U(x,xs,ω)≈

(4)

式(4)中：ΔL为高斯束中心间隔；ωr为参考角频率；ω0为初始高斯束宽度；θL、vL、pLx、pLz、TL分别表示以L为中心θ、v、px、pz、T对应的变量；Ds(L,pLx，ω)为以L为中心的高斯窗内地震叠加，表达为

(5)

最后应用互相关成像条件即可实现高斯束偏移，互相关成像条件的格林函数表达为

(6)

2 成像条件

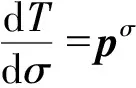
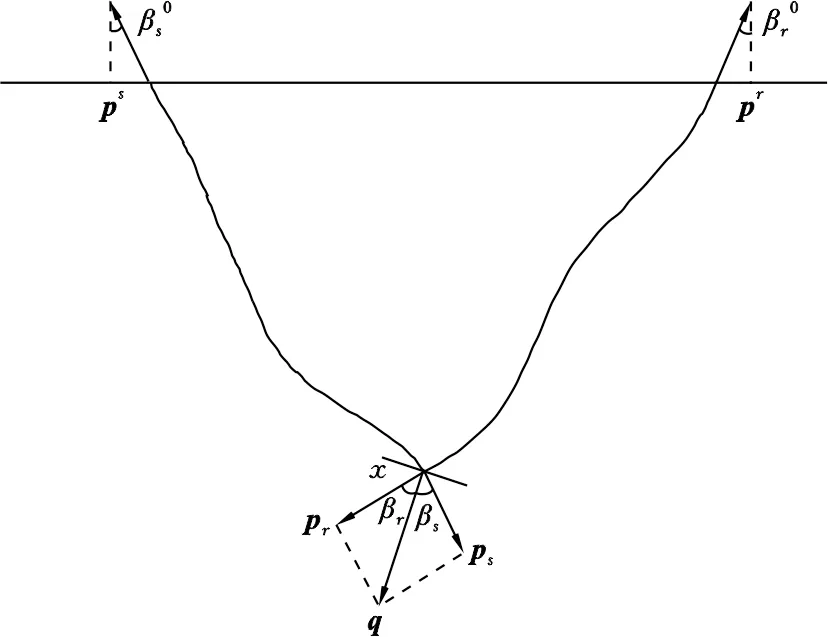
图1 射线偏移与射线向量示意图

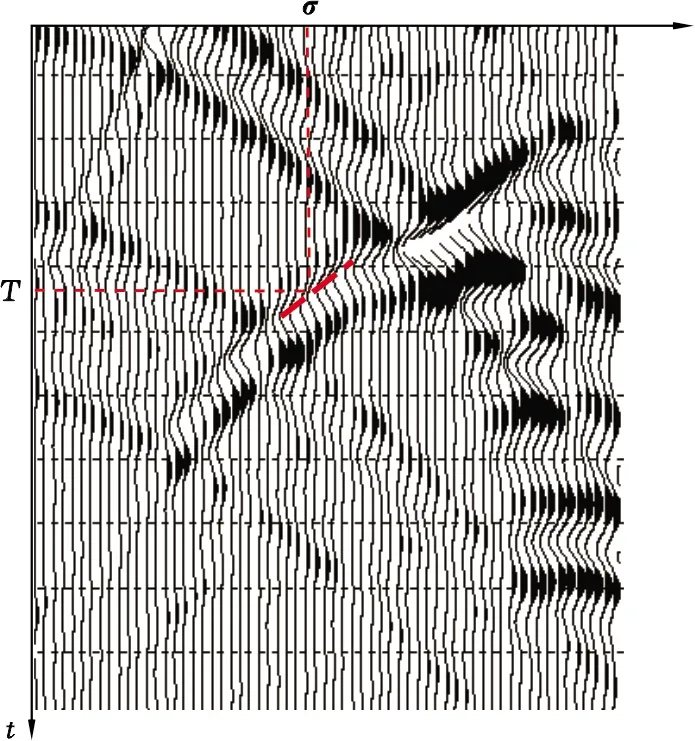
图2 地面射线向量求取示意图

(7)

对于覆盖次数为r的数据，Xu等[17]证明了上述成像条件的等价形式为

(8)

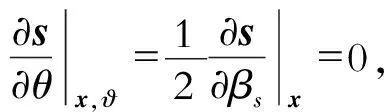
3 地下角度域波场分解与成像

在地震数据有效频带范围内，由于所选择的高斯束的初始宽度使走时和振幅在一个地震波长范围内缓慢变化[9]，在实际计算过程中，可以利用大网格计算走时和射线参数，然后利用其对成像的细网格进行插值得到走时和射线参数，以提高计算效率。假设粗网格上下左右4个网格点上的走时分别为tu、td、tl、tr，网格纵向与横向的步长分别为Δx、Δz，网格点中心处的走时为tm(图3)，对走时进行双曲展开，则上、下、左、右4个点处的走时可以表示为网格中心点处的走时如下[16]：

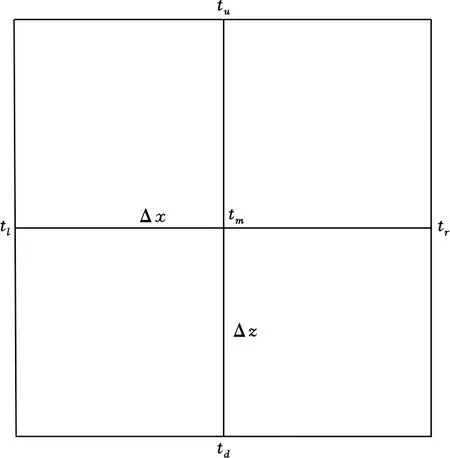
图3 粗网格示意图

(9)

式(9)中：gx为走时在水平方向一阶导数；gxx为走时在水平方向二阶导数；gz为走时在垂直方向一阶导数；gzz为走时在垂直方向二阶导数。可以进一步推导出射线参数表达式为

(10)

射线与垂直方向的夹角θ可以表示为

(11)

在求得粗网格点处射线角度以后，通过对粗网格点上的射线角度进行插值便可以求出成像网格点上的入射射线角度θs及反射射线角度θr，进而求出地下局部反射角θi=|θr-θs|/2，然后根据地下局部反射将成像结果求和在共成像点道集所对应的角度范围，得到地下局部共反射角度域道集，最后将地下局部共反射角度域道集所有角度进行叠加便得到最终的成像结果。

4 数据测试

首先通过一个包含水平及倾斜界面的理论模型Ⅰ分析常规入射角道集与地下局部共反射角道集的差异，速度模型如图4所示，采用海上拖缆采集观测系统，放炮方向从左到右，最大偏移距为6 000 m，最小偏移距为0 m，炮间距为25 m。图5为克希霍夫偏移与地下局部共反射角道集偏移成像对比，可以看出，对于模型I，二者成像结果相差不大。图6为克希霍夫偏移与地下局部共反射角道集偏移角度域道集对比，可以看到，对于水平地层，共入射角道集与地下共反射角道集基本相同，而对于倾斜地层，共入射角道集能量分布范围与水平地层能量分布范围一致，地下共反射角道集能量分布范围明显减小，地层倾角越大，其角度范围越小。由于角度范围存在差异，叠前AVA分析则会产生误差。由于叠前AVA分析是基于共反射角的，因此，对于倾斜地层，地下局部角度域道集才能满足AVA理论假设。

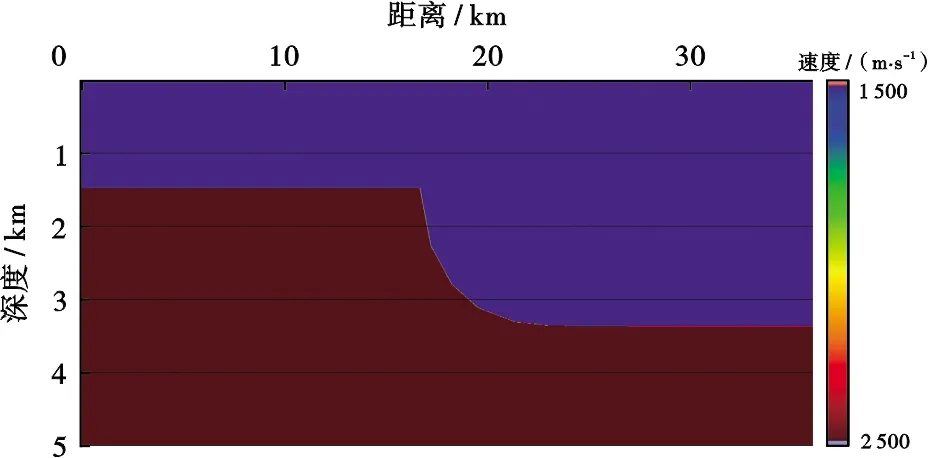
图4 理论模型I

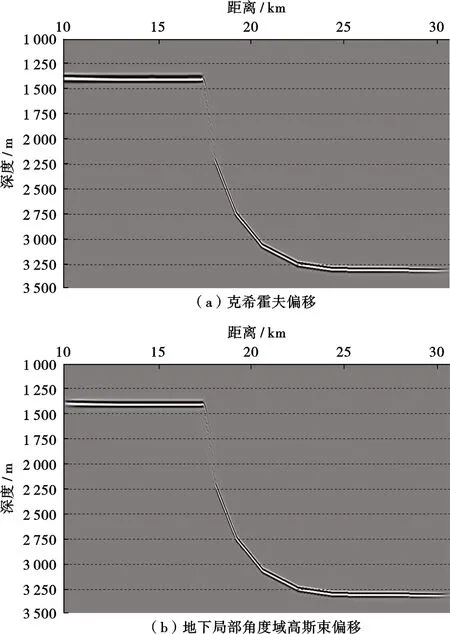
图5 理论模型I的偏移成像对比

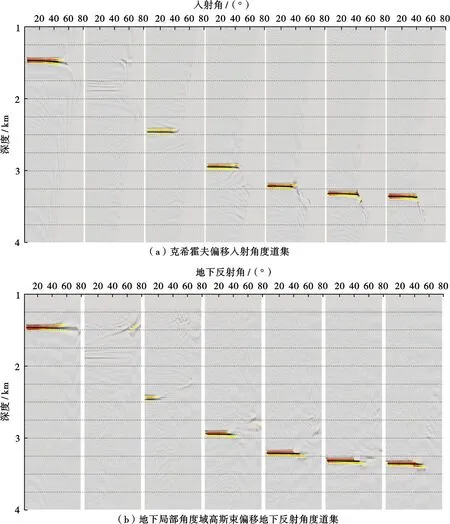
图6 理论模型I的偏移道集对比

然后通过Marmousi复杂模型来测试本文偏移算法对复杂构造的成像能力，所采用的采集观测系统与上述理论模型一致，偏移速度为真实速度采用50 m×50 m大小窗口滑动平均平滑后的速度(图7)。从图8中可以看到，克希霍夫偏移对复杂断块下伏构造难以有效成像。其成像结果表现为高角度偏移噪音，而地下局部角度域高斯束偏移则可以对其进行较好地成像，此外，复杂断块内部(图中椭圆形标注区域)，克希霍夫偏移也存在较多偏移画弧噪音，尤其是复杂断块底部，其断面及断块基本无法成像，而地下局部角度域高斯束偏移结果断面归位准确、断块清晰分块性较好。图9为图8中虚线处的偏移道集，其道集均为角度域道集，对于非复杂构造区域，克希霍夫偏移道集与地下局部角度域高斯束偏移道集相差不大，对于复杂断块内部及下伏区域，克希霍夫偏移角道集无连续反射同相轴，主要以高频噪音为主，而地下局部角度域高斯束偏移道集信噪比较高、同相轴比较连续，此外，受上覆复杂地层影响，其反射角均比较大，其角度道集能量主要分布在大角度范围。与层状模型不同的是，对于复杂构造，其能量分布范围并非是集中在小角度范围，其角度分布范围与构造及观测系统相关。因此，要想得到较为可靠的叠前AVA分析结果，传统的克希霍夫偏移距道集转换的入射角度道集可能不再满足叠前AVA理论，须采用地下共反射角道集。

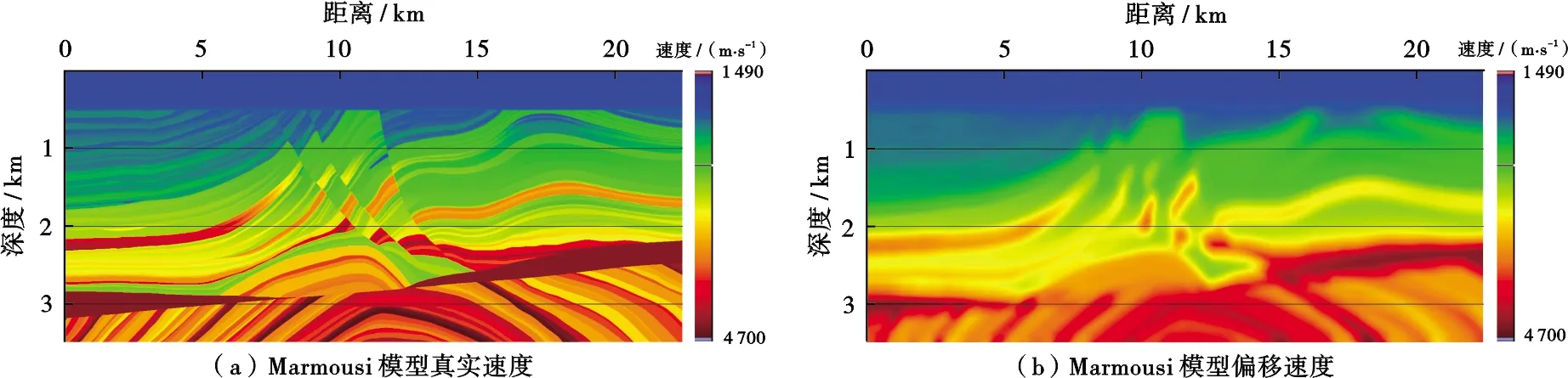
图7 Marmousi模型速度及偏移速度

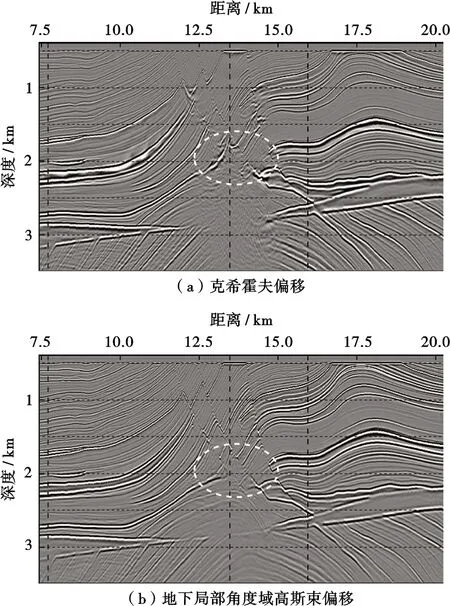
图8 Marmousi模型偏移成像对比

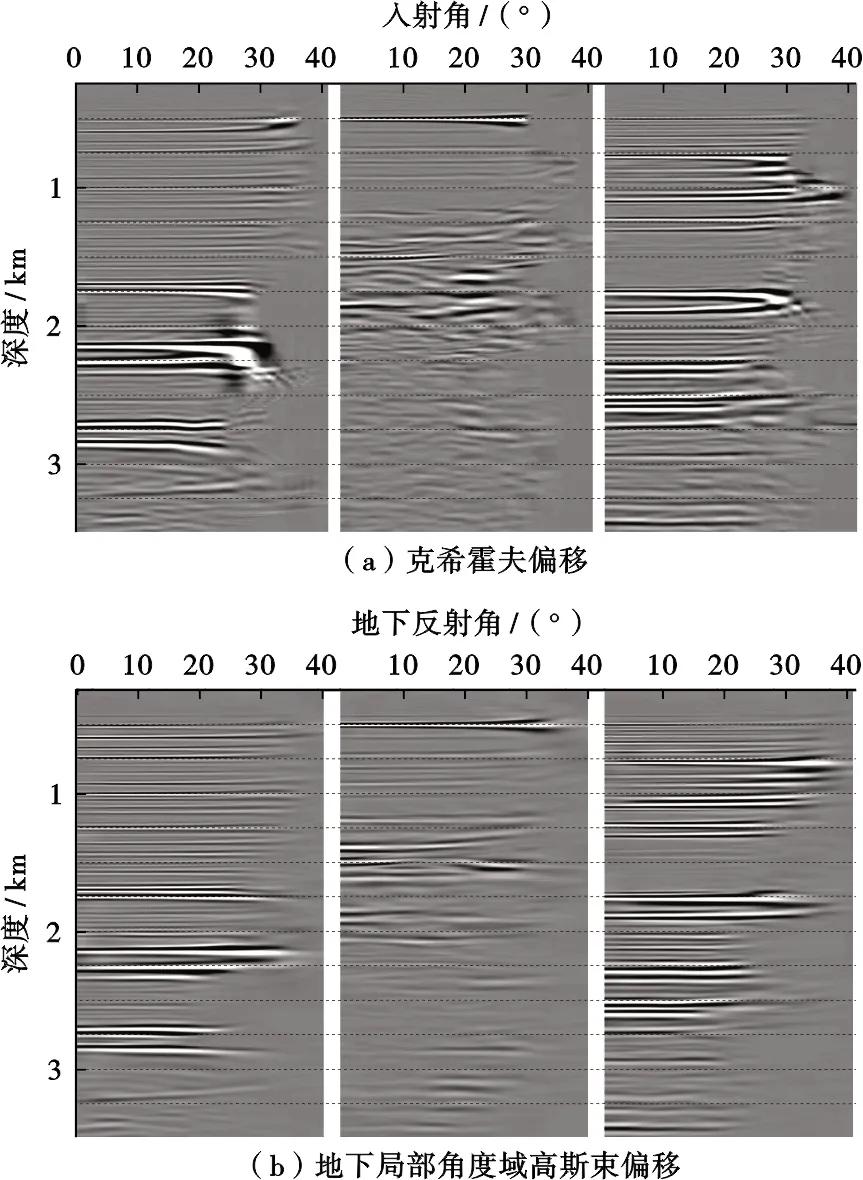
图9 Marmousi模型偏移道集

最后对实际数据的克希霍夫与地下局部角度域高斯束偏移成像进行对比(图10)，两者所使用的偏移速度相同。从图10可以看到，地下局部角度域高斯束偏移成像信噪比明显高于克希霍夫偏移成像，浅层同相轴连续性更好；复杂断块内部断块成像分块性更好，该区域断块油气藏地质认识更加清楚，有助于复杂断块内部油气勘探挖潜；断面成像更加清楚，断点更加干脆，箭头所指处为克希霍夫偏移无法成像的小断层，地下局部角度域高斯束偏移成像却非常清楚。

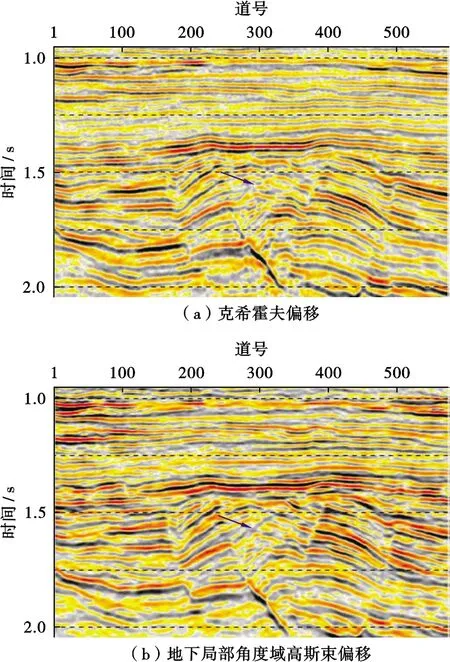
图10 复杂断块实际数据偏移成像对比

5 结论

为了解决克希霍夫偏移针对复杂构造成像能力不足及实际数据处理时效需求，本文研究了计算效率较高的地下局部角度域高斯束偏移方法。文中所述方法综合了射线偏移高效、高斯束偏移高精度、地下角度域成像高保幅保真的特点，具有较高的实用性。模型数据及实际数据计算表明，针对复杂构造，本文偏移方法极大地减少了偏移假象，成像质量明显优于克希霍夫偏移。此外，地下角度域道集表现出了高保幅保真特点，复杂构造道集信噪比及连续性明显高于克希霍夫偏移入射角道集；道集反射能量分布亦不同于克希霍夫偏移入射角道集，而是与观测系统及地下构造形态相关，为真实地下反射角道集，更加适合叠前AVA分析。