考虑扭矩影响的弯曲井眼内钻柱屈曲特性分析
庞东晓,卢 齐,邓 虎,彭 炽 ,付建红
1.中国石油川庆钻探工程有限公司钻采工程技术研究院,四川 广汉618300
2.油气藏地质及开发工程国家重点实验室·西南石油大学,四川 成都610500
引言
在石油工程中,钻柱是十分重要的井下工具,其屈曲行为对钻完井、测井等工程作业有着重要影响。钻柱屈曲是复杂的多次变形非线性力学问题,当钻柱发生屈曲后,其构型会随轴向载荷增加而变化;同时,随着钻柱轴向载荷的增加,钻柱会发生“锁死”,导致钻压传递困难、钻柱疲劳破坏等井下复杂情况。随着水平井、大位移井、多分支井等技术的广泛应用,弯曲井眼内的钻柱屈曲问题日益严重,亟需得到解决。由于钻井过程中钻柱受力复杂,影响钻柱屈曲特性的因素众多,不同情况下对应的屈曲临界载荷也会不同,这将不利于匹配钻井工具和预防钻柱屈曲,降低了水平井、大位移井的机械钻速。因此,有必要准确分析弯曲井眼内钻柱屈曲特性,研究钻柱受力及变形情况,避免钻柱出现屈曲。
国外针对钻柱屈曲的研究出现较早,1950 年,Lubinski[1]通过能量法推导了直井段的钻柱螺旋屈曲临界载荷计算方程,通过假设螺旋屈曲变形函数,得到了螺距与轴向载荷的关系式。Dawson 等[2]在分析钻柱屈曲时考虑了钻柱自重的影响,结合位移变形假设,建立了钻柱正弦屈曲的力学模型,给出了正弦屈曲临界载荷的表达式。Wu[3]研究了直井、斜直井和等曲率井中压扭钻柱的屈曲问题,发现扭矩使得钻柱的弯曲应变能增加,会造成屈曲临界载荷减小。Mitchell[4-5]研究了直井和斜直井中钻柱发生屈曲后的位移函数,确定了与屈曲构型相近的函数表达式,得到了对应的正弦和螺旋屈曲临界载荷。Menand 等[6]首次采用小尺寸钻柱进行了模拟实验,发现旋转会影响钻柱转动惯量,使钻柱受力变形增加,屈曲临界载荷降低。Wilson 等[7]根据摩阻扭矩对比分析,认为钻柱在滑动钻进和下尾管时发生了螺旋屈曲,通过数值模拟得出了下入完井管柱时全井段的3D 接触力云图。Gulyayev 等[8]推导了弯曲井段的钻柱屈曲方程,计算了弯曲井段中钻柱的屈曲临界状态。Cebeci 等[9]利用有限元方法分析了深井和超深井中多种钻具组合的屈曲问题,研究了屈曲临界条件的影响因素。Miska等[10]引入径向约束边界条件,分析了钻柱在水平井眼中的屈曲临界载荷。Chen 等[11]考虑了钻井过程中的摩阻和扭矩,基于动力学模型模拟了钻柱发生屈曲前后的状态,讨论了钻井过程中的钻柱屈曲风险。
国内方面,高国华等[12]利用空间几何理论和静力平衡法,推导了弯曲井眼内钻柱发生屈曲后的四阶非线性微分控制方程。刘凤梧等[13]考虑了横向约束的边界条件和扭矩作用,发现钻柱在压扭作用下的螺旋屈曲方向与扭矩相同,扭矩降低了钻柱屈曲临界载荷。刘峰等[14]采用有限元法,求解了等曲率井中钻柱螺旋屈曲的准静态加载问题,数值验证了模型的合理性。朱炳坤[15]考虑了水平井眼内钻柱的结构和工作环境,分析研究了水平状态下的钻柱屈曲问题,推导了水平钻柱屈曲临界压力表达式及对应的屈曲特征方程。董永辉等[16]建立了弯曲井眼中的钻柱模型,考虑了重力、曲率半径、钻井液浮力、井眼轨迹等因素,分析了钻压、钻速等参数对钻柱挠度的影响。何小宝[17]基于DQE 方法,对斜直段钻柱的屈曲特性进行了计算分析。黎伟等[18]用有限元软件对钻柱屈曲问题进行了模拟研究,确定了钻柱发生屈曲位移的最大点以及钻柱屈曲的临界载荷。徐春铃等[19]建立了斜直井中钻柱螺旋屈曲非线性有限元分析模型,研究了重力、扭矩和井斜角对临界载荷的影响。胡华等[20]通过分析造斜段钻柱受力,发现随着井眼曲率半径变小,钻柱正弦和螺旋屈曲临界载荷都增加,钻柱越不容易失稳。邬柯等[21]通过分析井下钻柱的几种屈曲形式,推导了垂直井和水平井中钻柱正弦与螺旋屈曲临界载荷的数学模型,为现场预测钻柱稳定性提供了理论依据。廖振武等[22]建立了钻柱螺旋屈曲诱发扭矩的计算模型,弥补了钻柱螺旋屈曲强度分析方法的不足。赵永安等[23]针对“三超”气井内管柱的屈曲行为,分析了导致管柱屈曲的关键影响因素,给出了屈曲临界载荷计算公式,探讨了临界屈曲条件下弯曲角、弯曲应力、狗腿度和扭矩的计算方法。秦桦等[24]在考虑诱发扭矩的情况下,建立了压扭组合作用下的钻柱螺旋屈曲微分方程。谭雷川等[25]基于能量耗散原理,建立了一种考虑钻柱正弦屈曲的套管磨损预测模型。
从国内外学者的研究可以看出,研究钻柱屈曲特性主要采用有限元法、微分方程法及室内实验法等。理论分析方法可以计算弯曲井眼内钻柱屈曲构型,但无法得到不同井深处全尺寸钻柱的屈曲形态,室内实验很难模拟弯曲井段屈曲特性。相较之下,有限元法不限制钻柱几何形状,且具有物理概念清楚、简单、无规格尺寸要求等优点,采用有限元方法模拟弯曲井眼内的钻柱屈曲是一种可行的思路。采用理论推导和有限元数值模拟相结合的方法,对考虑扭矩影响条件下弯曲井眼内钻柱的屈曲特性进行了分析,结果有望为水平井、大位移井弯曲井眼内钻柱设计、屈曲控制和强度校核提供参考,同时,为优化钻柱结构和钻井施工措施提供理论指导。
1弯曲井眼内钻柱屈曲微分方程
本文基于弯曲井眼内钻柱几何关系、力学平衡方程和受力关系,推导考虑扭矩影响时的钻柱屈曲微分方程,分析钻柱正弦屈曲和螺旋屈曲变形,钻柱屈曲临界载荷的数值解可以对比验证有限元模拟结果。
1.1考虑扭矩影响的钻柱屈曲微分方程
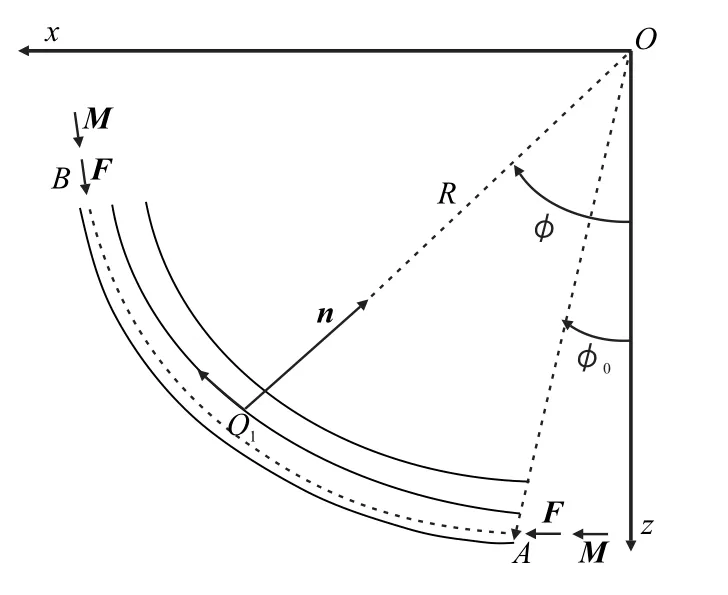
图1弯曲井眼钻柱几何关系Fig.1 Drill string geometry ina curved hole
建立如下坐标系:参考坐标系Oxyz,其单位向量为(i,j,k);自然空间坐标系O′nbτ,其单位向量为(n,b,τ),r1为钻柱在轴线上某一位置处的矢径,弧长为s;随动坐标系O′′e1e2e3,其单位向量为(eee1,e2,e3),可与自然坐标系相互转化。
(1)几何关系
假设在弯曲井眼中钻柱与井壁存在连续接触,钻柱轴线上的任一点C组成半径为rc的圆柱面。约束钻柱有效半径rc等于约束井眼内径与钻柱外径之差。令钻柱相对于初始位置的转角为θ。
相对于参考坐标系,井眼轴线上任一点O1的矢径等于

相对于随动坐标系,钻柱轴线上任一点C的矢径等于

(2)平衡方程
在弯曲井段弧长s处,截取钻柱微元ds。微元单元所受分布作用力fds(r为s处矢径),内力矩、内力分别为−MMM和−FF;s+ds处矢径为rrr+drrr,内力矩和内力为−M+dM和−F+dF。由单元受力平衡,可得

(3)物理关系
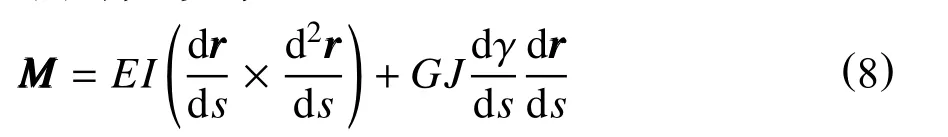
令F3=F,则钻柱截面内扭矩Ms为

根据弯曲井眼内钻柱的几何关系、平衡方程和物理关系,得到钻柱屈曲微分方程为
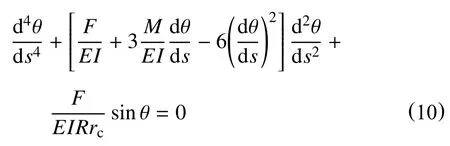
1.2 钻柱正弦屈曲分析
当钻柱发生正弦屈曲,可以假设其构型函数为θ=A′sin ξ。钻柱屈曲微分方程(10)所对应的正弦屈曲构型方程可以利用伽辽金法推导得到
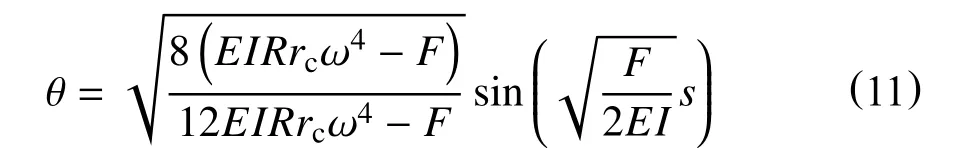
从式(11)可以看出,钻柱发生临界正弦屈曲的构型与扭矩无关,只由钻柱的轴向载荷所决定。然而,扭矩会直接影响正弦屈曲临界载荷和接触力的大小。
令A′=0,可以得到钻柱发生正弦屈曲的临界轴向载荷(F=EIRrcω4),临界载荷Fcrs的表达式为

钻柱保持正弦屈曲平衡状态的条件还包括接触力大于等于零,即nmin≥0。将nmin≥0 和式(13)联立可以计算钻柱保持正弦屈曲稳定状态的最大载荷,该载荷也会受到钻柱所受扭矩的影响。此处在求取构型方程是采用的是简单屈曲构型函数θ=A′sin ξ,导致了一定的误差。为提高结果精度,可以尝试采用θ=A′sin ξ+bsin(3ξ)。
1.3 钻柱螺旋屈曲分析
当弯曲井眼中钻柱发生螺旋屈曲时,对应的螺旋屈曲构型可以采用摄动法求解
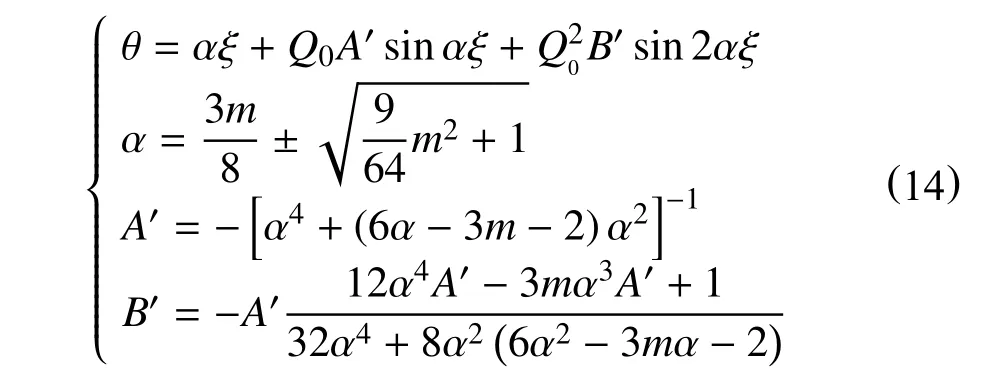
弯曲井眼中钻柱发生螺旋屈曲时,其临界状态同样可以采用nmin≥0 进行约束,方程中含有扭矩项,体现了扭矩对螺旋屈曲的影响。可以看出,扭矩对螺旋屈曲构型影响较大,螺旋屈曲和轴向变形均随扭矩增大而增大。
2 弯曲井眼内钻柱屈曲有限元模型
第1 部分推导的钻柱屈曲微分方程可以计算弯曲井眼内钻柱屈曲特性,但无法得到不同井深处全尺寸钻柱的屈曲形态。因此,需要建立钻柱几何非线性有限元模型,模拟考虑扭矩影响的钻柱屈曲变化过程。
2.1 几何模型与参数设置
在CAD 中建立弯曲井眼和钻柱的几何模型,如图2a 所示,弯曲井眼总长300 m,井眼直径215.9 mm,钻杆外径127.0 mm,壁厚9.2 mm。将几何模型导入Abaqus 中,先将钻柱和井壁离散为空间梁单元,然后利用结构性网格对模型进行划分。划分好的网格如图2b 所示,经网格无关性测试,网格数目和精度能达到模拟要求。钻柱的泊松比设定为0.3,弹性模量为210 GPa。

图2 几何模型及网格化分Fig.2 Geometry model and mesh generation
2.2 边界条件
将钻柱视为梁单元模型,钻柱与井壁的接触设为刚性接触,滑动边界光滑,不考虑井筒变形。轴向压力施加在钻柱顶端,考虑重力的影响,钻柱的扭矩施加在井口位置。钻柱底端只约束横向位移,钻柱顶端和井壁均为全约束。在井底径向上施加0.01 m的初始位移扰动。
3 弯曲井眼内钻柱屈曲特性分析
3.1 数值模拟与理论计算钻柱屈曲临界载荷对比
将通过数值模拟得到的弯曲井眼(包括增斜和降斜井段)内钻柱正弦和螺旋屈曲临界载荷与理论计算得到的解析解进行对比,以证明钻柱屈曲有限元模型的准确性和合理性。
不同造斜率时,平均井斜角60°、φ215.9 mm 弯曲井眼内φ127.0 mm 钻杆的屈曲临界载荷模拟值与计算值如表1 所示。
图3 为增斜和降斜井段中钻杆正弦和螺旋屈曲临界载荷模拟值与理论计算值的对比曲线。从图3和表1 可知,数值模拟值和理论计算值吻合得较好,相对误差在15%以内,满足工程精度要求。具体来看,在增斜和降斜井段数值模拟得到的正弦和螺旋屈曲临界载荷均小于理论计算值,屈曲临界载荷模拟值和计算值在增斜和造斜井段随井眼曲率有相同的变化趋势,正弦屈曲临界载荷误差小于螺旋屈曲临界载荷,这可能是螺旋屈曲理论模型过于简化导致的。同时,由表1 可以看出,降斜井段屈曲临界载荷很低,十分容易发生屈曲。总的来说,数值模拟结果与理论计算值存在一定误差,但参数变化规律相同,具有足够的准确性。

表1 不同造斜率下钻杆屈曲临界载荷对比Tab.1 The comparison of critical buckling load for drilling pipe under various buildup rate
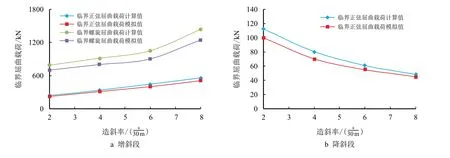
图3 不同造斜率下钻杆屈曲临界载荷对比曲线Fig.3 The comparison of critical buckling load curve for drilling pipe under different buildup rate
3.2 增斜井段钻柱屈曲特性分析
(1)不考虑扭矩影响的钻柱屈曲特性
为了对比扭矩对钻柱屈曲特性的影响,进行了不考虑扭矩条件下的钻柱屈曲数值模拟。不同轴向载荷作用下的增斜井段钻柱屈曲模拟结果如图4所示,由于重力的作用,弯曲井眼内的钻柱在中下部会与下井壁接触,随着轴向载荷增加,钻柱逐渐发生变形,其在弯曲井眼内的整体形态也随之发生变化。一般认为,钻柱截面角位移在30°以内属于正弦屈曲,超过30°则属于螺旋屈曲。
从图4 中可以看出,当施加的轴向载荷为450 kN(图4a)时,钻柱顶端发生初始正弦屈曲变形,正弦屈曲临界载荷为450 kN。同时,钻柱底部仍为平衡状态,这是因为钻柱与井壁间的摩擦妨碍了轴向载荷的传递。随着轴向载荷进一步增加到730 kN(图4b),钻柱处于正弦屈曲和螺旋屈曲之间的过渡状态,正弦屈曲即将失去稳定状态,钻柱变形向着螺旋屈曲发展。当轴向载荷达到810 kN时(图4c),钻柱上部产生了第一段完全的螺旋屈曲,钻柱螺旋屈曲临界载荷为810 kN。当轴向载荷超过螺旋屈曲临界载荷后(图4d),钻柱顶部附近的螺旋屈曲加剧,而中部附近的部分钻柱处于正弦屈曲与螺旋屈曲之间的过渡阶段。
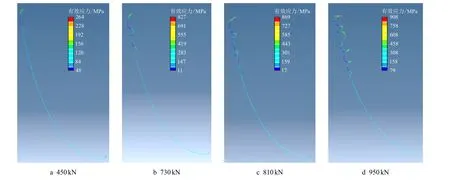
图4 不考虑扭矩影响时不同轴向载荷下增斜井段钻柱屈曲特性Fig.4 The buckling characteristics of drilling pipe at build-up section under different axial loads without the consideration of torque
另外,钻柱底部始终没有发生屈曲变形,一直处于平衡状态。这是因为在增斜井段中,钻柱主要在造斜点附近发生屈曲,由于钻柱与弯曲井眼接触产生的摩擦力,轴向载荷无法有效传递到钻柱底部。随着轴向载荷增加,顶部钻柱首先发生初始正弦屈曲变形,在一定的轴向载荷范围内,上部钻柱的正弦屈曲处于稳定状态,随后转变为完全的螺旋屈曲。此后,中部钻柱也逐渐从正弦屈曲向螺旋屈曲转变。
(2)考虑扭矩影响的钻柱屈曲特性
扭矩载荷为4 kN·m,不同轴向载荷条件下的增斜段钻柱屈曲特性如图5 所示。和不考虑扭矩的情况(图4)相比,钻柱变形的发展规律类似,扭矩对增斜井段钻柱的屈曲变形影响较小。当施加的轴向载荷达到430 kN(图5a)时,钻柱顶端出现初始正弦屈曲变形,钻柱正弦屈曲临界载荷为430 kN,略小于不考虑扭矩影响时的临界载荷。当轴向载荷增加到570 kN(图5b),钻柱处于正弦屈曲和螺旋屈曲之间的过渡状态。扭矩载荷为4 kN·m 时的螺旋屈曲临界载荷为780 kN(图5c),当轴向载荷超过螺旋屈曲临界载荷后(图5d),钻柱的螺旋屈曲加剧。和不考虑扭矩影响时的情形类似,底部钻柱始终处于平衡状态,不发生屈曲变形。总的来说,考虑扭矩影响时的正弦和螺旋屈曲临界载荷均小于不考虑扭矩影响时的临界载荷,且临界载荷随扭矩增加不断降低(表2)。扭矩使钻柱单元所受应力增加,当增大轴向载荷时,钻柱屈曲变形不断延伸。同时,施加的扭矩使钻柱刚度减小、螺旋角位移增大,从而提前发生正弦和螺旋屈曲。

表2 增斜井段不同扭矩载荷下的钻柱屈曲临界载荷Tab.2 The critical buckling loads of drilling pipe at build-up section under different torque loads
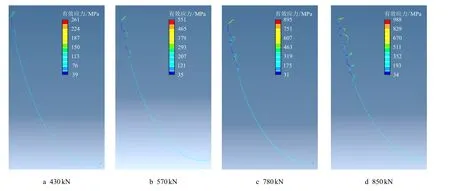
图5 考虑扭矩影响时不同轴向载荷下增斜井段钻柱屈曲特性Fig.5 The buckling characteristics of drilling pipe at build-up section under different axial loads with the consideration of torque
3.3 降斜井段钻柱屈曲特性分析
(1)不考虑扭矩影响的钻柱屈曲特性
图6 为不考虑扭矩影响时的降斜井段钻柱屈曲模拟结果。当轴向载荷为40 kN 时(图6a),钻柱整体几乎没有发生变形。当轴向载荷为120 kN时(图6b),钻柱下部发生初始正弦屈曲,正弦屈曲临界载荷为120 kN。随着轴向载荷增加到300 kN(图6c),上部钻柱也出现了严重的正弦屈曲,同时下部钻柱处于正弦屈曲向螺旋屈曲过渡的状态。当轴向载荷增大到400 kN(图6d),上部钻柱的屈曲变形更加明显,下部钻柱发生了螺旋屈曲,钻柱螺旋屈曲临界载荷为400 kN。相比于增斜井段,降斜井段更容易发生屈曲,屈曲临界载荷大大小于增斜井段。降斜井段上部和下部钻柱均发生了较明显的位移,这和增斜段位移主要发生在上部钻柱有明显区别。

图6 不考虑扭矩影响时不同轴向载荷下降斜井段钻柱屈曲特性Fig.6 The buckling characteristics of drilling pipe at drop-off section under different axial loads without the consideration of torque
(2)考虑扭矩影响的钻柱屈曲特性
对钻柱施加与轴向力方向一致、大小为4 kN·m的扭矩载荷,不同轴向载荷下降斜井段钻柱屈曲特性如图7 所示。
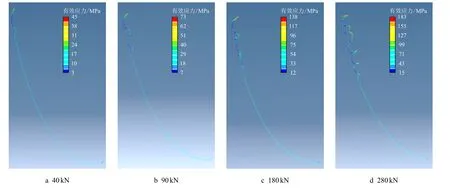
图7 考虑扭矩影响时不同轴向载荷下降斜井段钻柱屈曲特性Fig.7 The buckling characteristics of drilling pipe at drop-off section under different axial loads with the consideration of torque
当轴向载荷为40 kN 时(图7a),钻柱上部和下部已经产生了比较明显的变形。当轴向载荷增加到90 kN(图7b),钻柱上部发生初始正弦屈曲,正弦屈曲临界载荷为90 kN。随着轴向载荷增加到180 kN(图7c),上部和下部钻柱均产生了严重的变形,处于正弦屈曲向螺旋屈曲过渡的状态。当轴向载荷增大到280 kN(图7d),上部和下部钻柱均发生了螺旋屈曲,钻柱螺旋屈曲临界载荷为280 kN。扭矩的存在使上部钻柱在很小的轴向载荷作用下就发生了初始正弦屈曲,同时螺旋屈曲临界载荷也显著降低。相比于无扭矩作用时,正弦屈曲首先发生在钻柱上部,且上部钻柱正弦屈曲变形程度大于底部钻柱;螺旋屈曲同时出现在钻柱上部和下部,钻柱截面所受应力增大。相比于增斜井段,相同扭矩作用下降斜井段钻柱屈曲临界载荷大大减小,更容易发生屈曲。
在相同造斜率和平均井斜角条件下,不同扭矩载荷对应的钻柱正弦和螺旋屈曲临界载荷见表3。可以看出,正弦和螺旋屈曲临界载荷随着扭矩增大迅速减小,当扭矩为12 kN·m 时,屈曲临界载荷不到不考虑扭矩时的一半。这说明在降斜井段中,钻柱在扭矩作用下十分容易发生屈曲,需要特别注意。

表3 降斜井段不同扭矩载荷下的钻柱屈曲临界载荷Tab.3 The critical buckling loads of drilling pipe at drop-off section under different torque loads
4 结论
(1)钻柱正弦屈曲构型与扭矩无关,而只与钻柱所受轴向载荷有关,扭矩对螺旋屈曲构型影响较大,螺旋屈曲和轴向变形均随扭矩增大而增大。
(2)在弯曲井眼中,井眼曲率是影响屈曲临界载荷的重要因素,增斜段正弦和螺旋屈曲临界载荷随井眼曲率增大而增加,降斜段临界载荷随井眼曲率增大而减小。
(3)数值模拟得到的弯曲井段钻柱屈曲临界载荷与解析解的相对误差在15%以内,说明数值模拟结果具有足够的精度和可靠性。
(4)数值模拟结果表明,随轴向载荷增加,增斜井段钻柱从顶部部开始发生正弦和螺旋屈曲,钻柱底部依然保持平衡状态。施加扭矩后,钻柱刚度降低,螺旋角位移增大,正弦和螺旋屈曲临界载荷降低。钻柱正弦屈曲形态变化较小,扭矩对螺旋屈曲变形的影响更大。
(5)在降斜井段中,不考虑扭矩时,降斜段初始正弦和螺旋屈曲均首先出现在钻柱下部;考虑扭矩影响时,降斜段初始正弦屈曲出现在钻柱上部,初始螺旋屈曲同时出现在钻柱上部和下部。随着扭矩的增大,正弦和螺旋屈曲临界载荷显著减小。相对于增斜段,降斜段钻柱屈曲临界轴向载荷非常小,说明增斜井段发生屈曲的可能性较小,降斜井段很容易发生屈曲。
(6)弯曲井眼内的钻柱屈曲是一个极其复杂的现象,影响因素很多。如钻柱和井壁的摩擦会影响轴向力的传递,从而影响钻柱屈曲,钻柱的转动和钻杆接也会影响钻柱屈曲,在后续的研究中,建议重点考虑钻柱和井壁的摩擦对钻柱屈曲的影响。
符号说明



