斜向进水消力井水力特性模拟研究
焦 萱, 邱 勇, 龚爱民, 张华群
(云南农业大学 水利学院, 云南 昆明 650201)
1 研究背景
水利水电工程中泄水建筑物传统的消能方式(如底流消能、挑流消能、面流消能等)与地形、生态之间的矛盾日渐凸显,使得消能防冲技术逐渐由大面积水流冲击作用的外消能方式改为局部耐受的内消能方式[1]。
消力井的理念最先由郭子中[2]在20世纪80年代提出,并对井流消能的设计准则及尺寸确定方法进行了研究总结,而后国内外专家学者对其进行了广泛而深入的研究,如石胜友等[3]、孙高升[4]、刘春冬等[5]分别对不同型式消力井的设计及应用进行了研究;金瑾等[6]、邵国瀛等[7]、衡海龙[8]结合实际工程需要对消力井进行了改进分析;张宗孝等[9]、陈小威等[10]、解卫东等[11]开展直径、井深等局部结构尺寸变化下的水工模型试验研究;何军龄等[12]、Giudice等[13-14]采用试验研究的方法得到了井内流速、压强等水力指标的变化;衡海龙等[15]、冯博等[16]、Zhao等[17]对比研究了井式消能效率的变化;郭新蕾等[18]、Belgibayev等[19]、王滢等[20]在数值验证优化的基础上,开展了井内紊流流场的算法分析探究;张文传等[21]、栗帅等[22]、南洪等[23]通过数值模拟给出了竖井旋流消能相关水力特性要素的分布情况,上述研究主要以旋流式消力井、突扩/突缩式消力井等竖向进水方式为主。
由于消力井开挖衬砌复杂、边界脉动压力大、需要充分掺气、进出口不能同时满水等原因,制约了竖向进水消力井在山区峡谷型水库泄水建筑物的选择与应用。在山区地形多变的条件下,斜向进水、侧向泄水圆形消力井是一种相对经济有效的新型消能方式,其工程构造简洁、消能功效好、对地形的适应性强,但是此类型式的消力井应用研究成果较少[24]。笔者在文献[25]中基于物理模型试验对该类型消力井在一定泄槽纵坡下的井内淹没射流水力特性开展了机理解析,得到了射流沿程最大流速及冲击区井壁时均作用力的半经验公式。但由于物理模型试验的测量手段有限,通常难以观测到某些水力变量的极值且无法捕捉到一些随机出现、历时较短的水流特征,从而无法系统全面地揭示消力井内部水流复杂的水力特性。故拟依托相应边界体数理模型,采用ANSYS FLUENT 16.0仿真计算平台进行基于C语言的UDF模型变量布设及数值解的初始化加载编译求解,对物理模型试验成果予以补充,并进一步开展斜向进水、侧向泄水圆形消力井井内相关水力特性的研究。
2 水动力模型及数值计算
2.1 计算域
消力井内水流流态为典型的有固壁型剪切湍流运动(Re≥2 300)。为了更好地模拟实际湍流,以云南省山区某实际工程溢洪道及其下游消力井消能设施设计为蓝本,考虑影响系统行为变化的参变量(自然行为反应参数和扰动引发效应参数),在各向异性条件下引出概化非线性湍动区间组合,即以一定泄槽纵坡(i=1∶1.5)为区域标记,参考湍流近壁拟序结构给出近似边界条件[26],将入口断面沿上游移动,以实现给定随机脉动分布水流向下游传输的时间稳定推进过程,促使湍流得以正态充分发展,进而激活沿程梯度驻点传递的一致性;为了阻止流场全面线性激发下的侧向约束影响而得到平稳通量的自由界面,出口段参照外延节点累加嵌边法进行设计。消力井计算域体型设计如图1所示。
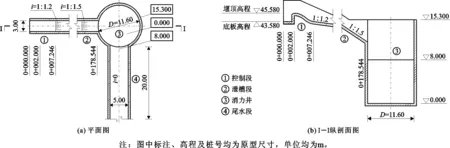
图1 实例工程消力井计算域体型设计图
2.2 网格剖分
消力井计算域几何拓扑为直角坐标系XOY下三维单连域范式,自由网格剖分采用分块体Fourier级数架结构化展开,柔性界柱和输运调节复杂区域应用Chebyshev多因次架O型剖分,局部参数变化剧烈点采用权函数Gauss-Lobatto进行渐变加密衔接[27]。参考Kolmogorov尺度平衡过程,为减少在离散衍生中分区算力工作,将空间节点关联延展至10η处(η为耗散尺度),邻近单元集合范数比值控制在1.2以内,按照数值计算优化比(整体1.414倍,局部2倍),其网格剖分方案见表1,消力井关键计算域网格剖分见图2。网格质量评判标准参考Jacoby阵列比值和最小节点单元体积,前者各积分节点比值均匀且无负值表现,均高于非物理畸变度量0.8;后者无反立方体积及退化分辨边长,满足不合容忍限度值;单元整体背离理想形状程度较小,映射网格非物理性存储质量较好。

表1 网格剖分方案
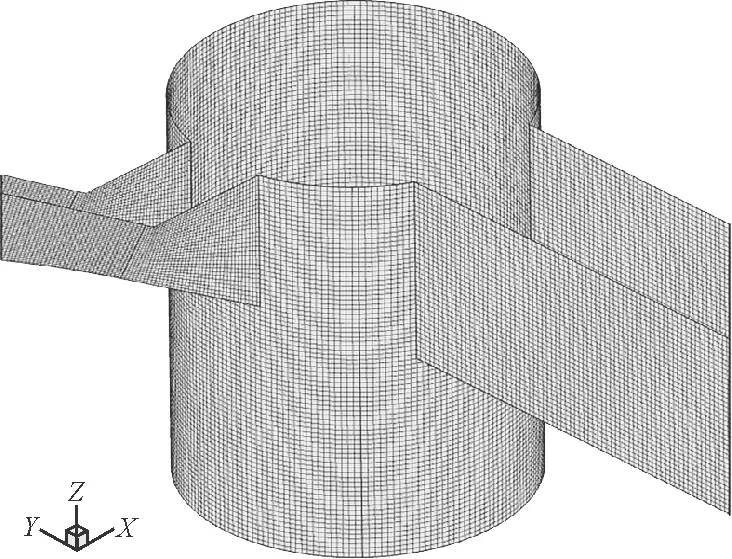
图2 消力井关键计算域网格剖分示意图
2.3 水动力数理模型
考虑到消力井内流体平均自由程远远小于消力井的特征尺寸,满足连续介质函数分析法假设。由Bradshaw假定结合湍流研究目的,选择雷诺模拟法和各态遍历定理对流场中相关随机变量进行数理统计,建立雷诺应力封闭方程组并进行数值求解。
2.3.1 控制方程组 掺气影响下的域内水流输运属于特征明显的水-气多相介质流,不同连续介质输运受控于应用Euler-Euler法的各自质量、能量和动量守衡方程,进而对Boussinesq假定下的N-S方程采用法向约束通量作零的系综平均,并优选k-ε两方程模式进行各向异性的侧向分离输运统计演化,得到三维渐近准则下的柱坐标雷诺应力方程组,并选用经验模式常数[28],其通式如下:
(1)
式中:ρ为体积分数加权平均密度,kg/m3;φ为通用变量;Γφ为φ的扩散系数;U和V分别为纵向轴(X方向)和径向轴(r方向)的速度分量,m/s;Sφ为源项。
比较目前常用的自由表面追踪方法,VOF法既有MAC法和标高函数法的优势,同时也修正了内存多、耗时久及坐标多值函数处理的问题。引入流场体积函数F,对应网格单元中具有相同的水、气特性张量场,其中与计算域填满介质气、含有水气介质交界面及填满水介质相映射的3类状态依次为:F=0、0≤F≤1、F=1,体积占比的算法平均表示其他水、气共存的不详量和特性参量。界面追踪即凭借该线性方程的梯度解析来进行几何重建并确定相应的对流过界位置,表示为[28]:
(2)
式中:u、v、w为不同方向的速度分量,m/s;VF、AX、AY、AZ为单位体积函数不同要素表征。
2.3.2 计算条件及算法设置 连续介质假设状态流动(考虑压强及温度叠加作用,参考流体动力学表征标准Ma<0.3)用非恒定流逼近恒定流稳定解的方法,域内计算条件包括初始条件和边界条件,水为主相、气为次相,各计算条件作如下处理:
(1)初始条件:求解初始时间步长水流条件由物理模型试验得到,其特征工况恒定流水位-流量关系见表2。井内预先存水与尾水渠底板平齐。

表2 恒定流水位-流量关系
(2)边界条件主要包含两类,一类是入口及顶部的本质边界条件,由水位-压强关系换算得到流速、压力等参数;另一类是出口及壁面的组合边界条件,其中出口为顺边界法向约束梯度为零的外推延展自由式出流,远场充分并与空气连通发展;壁面由牛顿内摩擦定律采用无滑移、无分离条件且近壁区黏性底层采用壁面函数法处理。以上k、ε值参考内流模型[27]等效确定。
(3)算法:考虑侧向泄水正应力约束施加,计算域内不同阶数张量采用有限体积法离散,二阶迎风格式进行差分求解。时间步长参考CFL条件及特征尺度(流速和流向最小网格尺寸)因素分析确定,压力及速度场分离耦合考虑采用瞬态PISO法进行隐式迭代校正求解,压力插值格式为PRESTO!,当单位时间步长内各离散化控制方程的标度残差均小于10-3时渐近满足;当体系流量净值小于输运总量的1%并且流场监测物理量精度稳定时,即实现求解平衡状态。
2.4 模型敏感性分析
2.4.1 网格剖分无关性 根据特征工况适应性分析,控制变量时间节点取为10 s,对应底板轴线处等间距监测3点坐标分别为(0.200,0.000,0.000)、(0.000,0.000,0.000)、(-0.200,0.000,0.000)。以不同剖分方案的网格数量N(表1)为自变量,选择流场物理量时均压强Pavg为因变量,对应监测结果如表3所示。

表3 网格剖分不同方案底板轴线处监测点相应的时均压强Pavg kPa
由表3可知,当网格剖分总数小于8.0×105时,相应监测点间时均压强值存在较大差异,但随着网格剖分数量的增加,时均压强值受影响变小且趋于稳定,综合考虑计算成本和数值计算误差,可近似认为总网格数量为9.0×105时即可满足与网格划分方案无关。
2.4.2 不同时间步长独立性 根据网格剖分无关性验证结果,取底板轴线处监测点(0.000,0.000,0.000),当时间步长Δt分别为0.001、0.005和0.010 s时,以时间步长Δt为自变量,流场物理量时均压强Pavg为因变量,不同时间步长相应的底板轴线处监测点时均压强如表4所示。
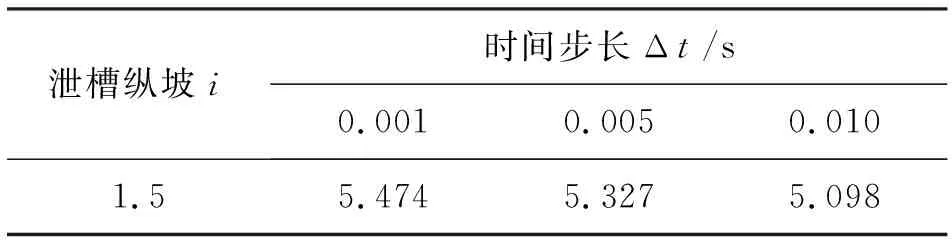
表4 不同时间步长底板轴线处监测点时均压强 kPa
由表4可知,不同时间步长对流场物理量求解结果影响不大,且均满足模型数值分析差分格式精度限值(12%),综合考虑网格剖分方案及数值计算误差,在保证计算资源和离散稳定的前提下,尽可能采用较大的时间步长,故选取Δt=0.010 s。
2.4.3 定解收敛性 区别于无湍流水动力数理模型,不同流体介质在湍流部分的矢量表达各不相同且相互耦合,故定解问题的矢量光滑解对任意系统条件下的时空行为特性表达至关重要。矢量光滑解是客观物理存在的真实写照,但从理论数值分析范畴来看,它们可能并不总是存在的[29-30]。非对称边界下湍流控制方程组主要包含质量、加速度及压力等项,由反证法假设控制方程组I(f)对任意时空集合条件S无矢量光滑解A(A→∞,I(f)n→∞),但对有限域下运动流体质子,由能量不等式得:
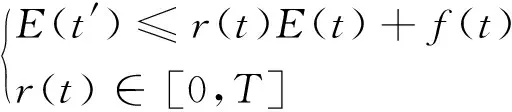
(3)
式中:E为能量函数;r(t)为参变函数;f(t)为组成控制方程;t′为区别t的不同运动时间,s;T为时间区间上限。
故控制方程组I(f)对任意时空集合条件S无矢量光滑矢量解A不成立,则有限域下,运动流体质子矢量理论加速受制于有限值且作用渐弱,即存在模型Leary弱解效应M:
(4)
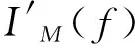
对所选定工况的离散化控制方程状态变量Φ,应用文献[31]中方程尺度的谱化分析法得到网格数N=902 177、时间步长Δt=0.010 s时的弱解残差收敛轨迹[31],如图3所示。
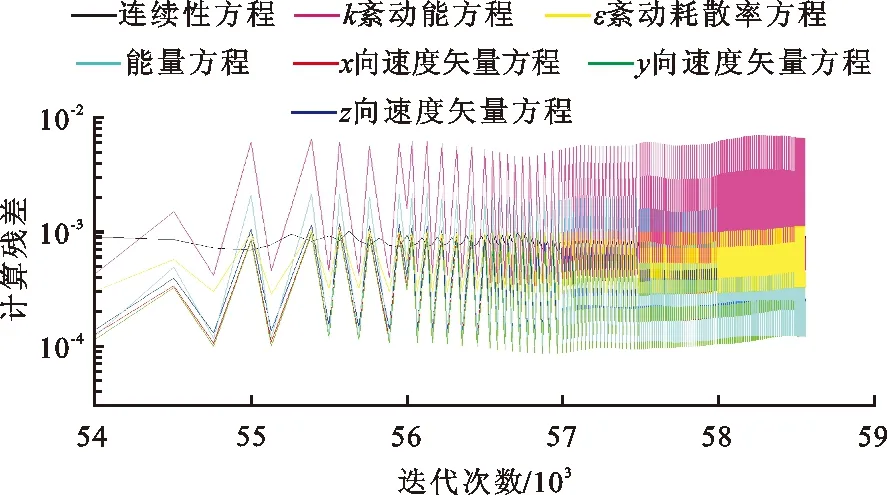
图3 计算残差收敛轨迹
由图3可以看出,伴随初始条件下控制方程组中不同方程变量的设置迭代,应用模型数值计算的一致有界性较好且满足算法渐进平衡状态要求,为离散差分的最优解近似控制方程组的理论解提供了基础,进而考虑在弱解系综平均的附加统计下,有条件地等效反求矢量光滑解函数,以实现研究问题的近似机理效应捕获描述,验证所建模型的可行性。
3 结果与分析
3.1 水流流态及转换机制
由模拟计算得到的对称进水方向特征断面(XZ面)水气多相分布数值结果见图4,图4中红色为水,蓝色为空气,水气交界面为绿色。
由图4(a)可知,水流沿泄槽段携带空气冲击下泄,消力井内形成强紊动掺气水流,主流在井内向四周扩散并与周围水体发生强烈剪切、摩擦、混掺,在底部潜流及上附壁射流作用下,形成了斜向淹没冲击射流与淹没水跃流的复合流态。井内水流结构沿射流方向可分为7部分(图4(b)):射流淹没区(Ⅰ)、冲击区(Ⅵ)、上、下附壁射流区(Ⅴ、Ⅶ)、底部潜流区(Ⅲ)、上、下部旋滚区(Ⅳ、Ⅱ),这与文献[4]的试验研究成果是相一致的。
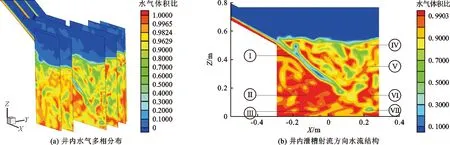
图4 消力井内水流流态及水气体积比分布云图
雷诺数是影响井内流态转换的主要因素,当雷诺数达到某一临界值时,流态即发生转换。沿程取关于射流轴线对称的近似符合动力自相似或自保持的高斯分布断面[4],推求得到射流沿程雷诺数(Re)分布如下:
(5)
式中:ρa为流场紊动水密度,kg/m3;C为关于矢量方差σ的参数矩阵;μmax为射流沿程最大流速,m/s;b为射流扩展长度,m;X′为X轴向归化映射坐标向量矩阵,即X′=U′X,其中U′为归化矩阵;X为X轴向坐标向量矩阵。
由近似正态概率密度函数性质可知,分别有概率为68%、95%、99.7%的数值分布在距平均值1σ、2σ、3σ范围内,结合图4分析水流流态转换主要包括3个过程:
(1)泄槽出口射流与空气边界相对运动产生平面横向紊动扩散,受剪切、摩擦以及大量空气掺入作用所产生的絮状自由扩散射流,以及水舌外缘随沿程边界层分离的水跃旋滚回流,在自由面作用下发生不连续或破碎,主流运动近似遵循平面直线扩散运动;
(2)底部为顺时针方向完整旋滚,上部为不连续破碎逆向旋滚,射流流向在近壁面附近发生改变,沿上、下边界附壁水舌内外缘分别与水体和空气接触,在不断混掺和摩阻作用下,产生近似淹没射流和冲击射流的附着扩散;
(3)有限边界条件下,射流正交各断面流量保持守恒[4],伴随着射流水股被下游水深淹没并与周围水体充分混掺、剪切、旋滚,水体产生加速运动使得区域内压强降低,冲击区附近壁面和底板水流受附着影响产生旋滚水跃。其空间各部分不同维度的演变变化方向为:
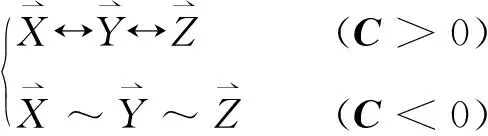
(6)
3.2 流速分布及形成机理
有限域斜向进水、侧向泄水条件下,特征工况消力井内的流速大小分布如图5所示。
由图5(a)可以直观地看出井内流场及射流沿程流速分布,取井内与射流沿程最大流速点连线为流速矢量线,忽略泄槽出口尚未充分发展的紊动混掺区内射流初始段对主流位置的影响,则简化为直线。由平面射流距出口不同距离的各断面流速分布可知,随着射流断面距离泄槽出口长度的增加,射流扩展长度也对应增加,流速矢量线上的最大流速umax沿横向和流向逐渐减小,纵向分布趋于平缓,横向分布由中间向两边递减。
沿流速矢量方向建立直角(xoy)坐标系(图5(b)):坐标系原点o位于泄槽出口面,沿淹没射流主流方向为x轴,垂直主流方向为y轴。根据紊动射流基本特征简化定常流Reynolds方程组,文献[4]已给出有限域射流沿程最大流速半经验公式,如公式(7)所示。
(7)
式中:x为主流轴线上的距离,m;h0为泄槽入池水深,m;u0为泄槽出口断面流速,m/s。
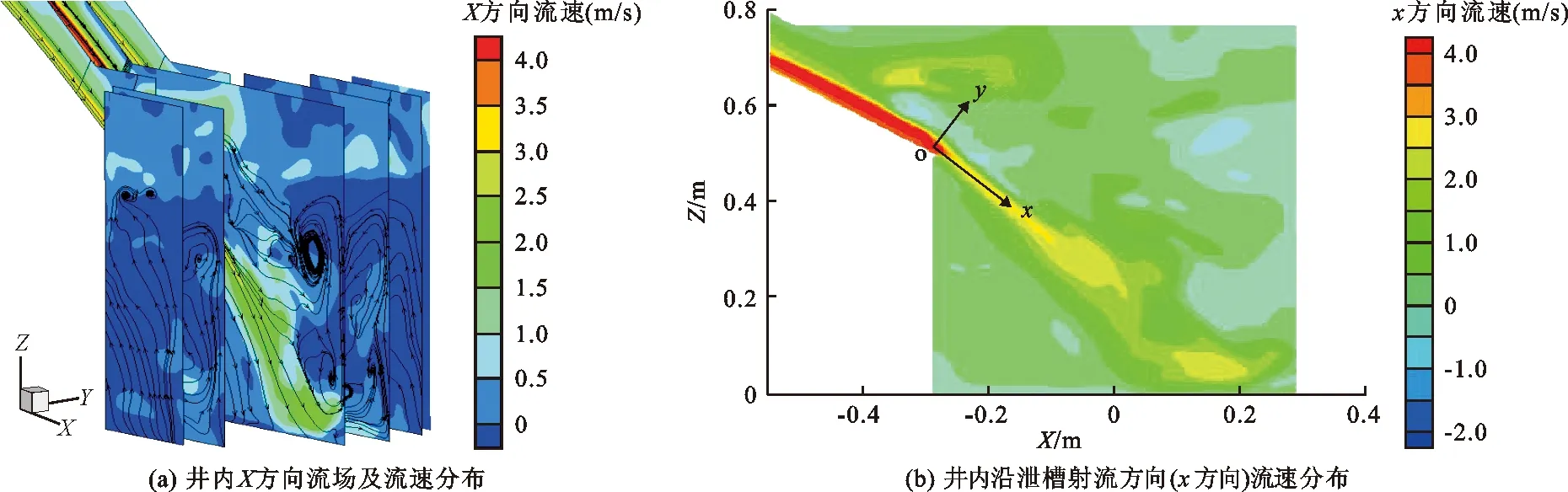
图5 特征工况消力井内流场及流速分布云图
将有限域模型模拟的最大流速计算值与公式(7)得到的特征工况射流沿程最大流速进行对比,结果见表5。
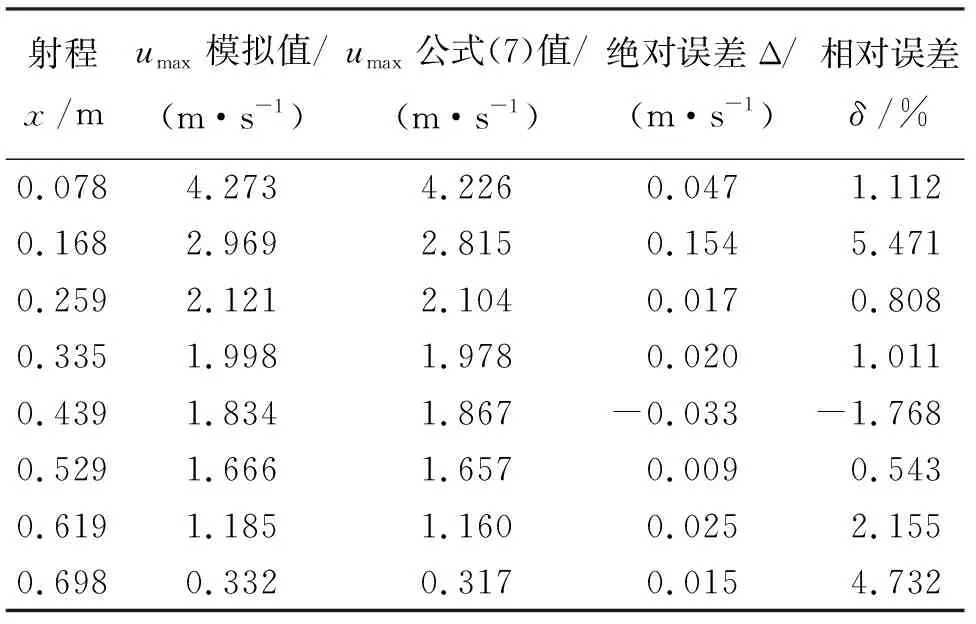
表5 消力井内射流沿程最大流速计算值与公式拟合值对比分析
由表5可知,射流沿程各点最大流速模拟值与公式(7)拟合值相比误差较小,且沿射程方向分布规律相同,即随着淹没水深的增加,射流动量沿程发生消散、转移、输运,流速逐渐减小。考虑到紊动射流是具有间歇性的复杂运动,其边界介于紊流和非紊流之间,取泄槽出口断面流速u0(m/s)为射流速度尺度,主流线上最大流速umax(m/s)与射流扩展长度b(m)的比值ω为流速分布特征尺度,则断面量纲为1的沿程流速分布为:
(8)
由公式(8)可看出,射流沿程流速大小分布是一族以最大流速为顶切点、流速梯度(∂u/∂y)调节的平面等值曲线,近似呈平面扩散规律。在水流运动过程中,由于黏滞作用,射流与环境流体在触发面相互混掺,带动周围局部流体共同发展,沿程更多流体的卷入使得射流厚度逐渐增大,断面流速分布趋于均匀。
3.3 压强特性及分布规律
有限域斜向进水、侧向泄水条件下,特征工况消力井内的压强分布如图6所示。
由图6可以发现,泄槽末端出现压力跌落,井内压强沿井深分层逐级增加且为正压;射流近井壁附近等值线较密,压力变化较大,结合局部流态分析,其原因在于冲击区内贴壁旋滚流冲击所致。
将计算得到的消力井底板时均压强与物理模型试验量测值相对比(图7)可以得出:物理模型试验最大压强值为6.695 kPa,计算最大压强值为6.692 kPa;计算值与试验值的最大误差为9.02%;消力井底板轴线平均时均压强计算值为5.616 kPa,与试验值5.760 kPa亦很接近。
为了更好地描述井内压强的分布情况,由Helmholtz动力学性质可知沿程断面矢量扩散不仅是伴旋滚拓扑变形运动的一种,而且在层次间面交互显著[26]。故考虑引入参考上表面形态的不同平面位置函数,令自由水面压强分布为P0(kPa),旋滚压强为PW(kPa),沿水深积分得:
(9)
式中:H为水深,m;g′0为自由面重力加速度,m/s2;X、Y、Z分别为位置坐标,m。
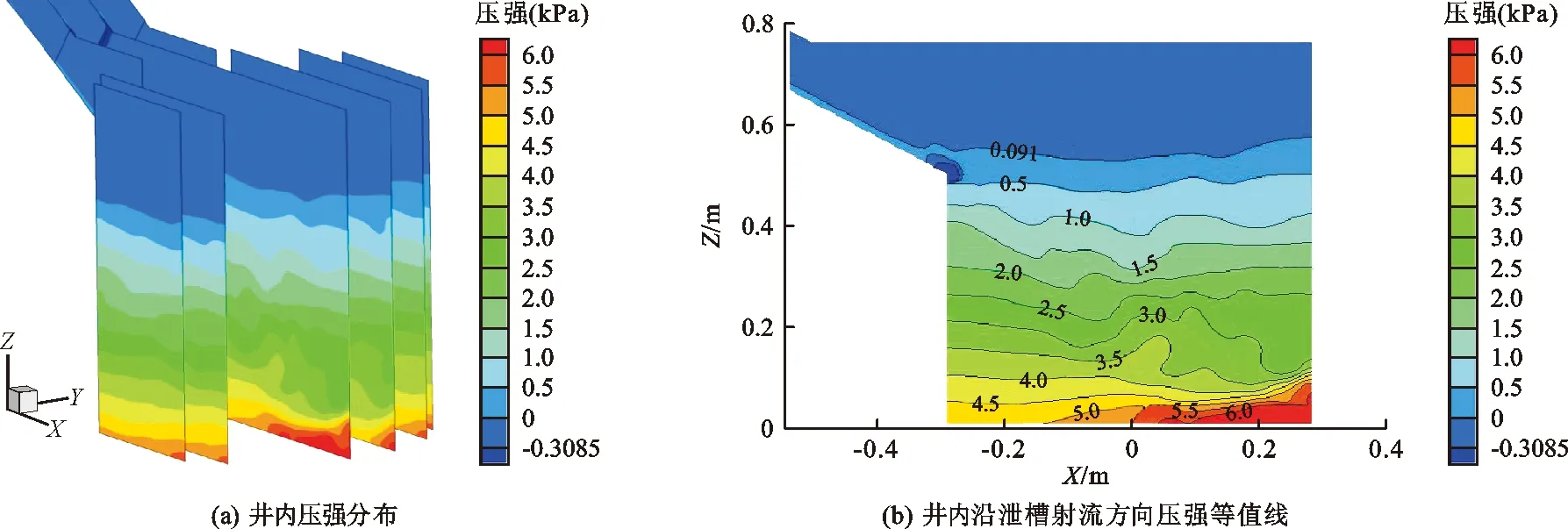
图6 纵剖面压强等值线分布
根据稳定旋滚运动特性及有界约束条件[32-34],在忽略科氏力Fc和层结关系⊆的影响下,对闭合迹线大多呈椭圆形状(特定情况为圆形)的Kirchhoff假定运动涡旋采用矢变归一化处理,以剔除个体及区域的旋滚压强PW变化差异,设涡旋中心为坐标原点,长、短轴分别为x′、y′轴,则其附加压强场水平及竖直结构分布如下:
(10)
式中:R(rn)为附加统一径向结构函数,其中rn为径向结构函数变量限制序列表征;H(Z)为附加统一振幅函数;an、bn分别为沿程射流卷吸涡旋的归一化长、短轴;Zn为引入纵波和横波的不同传播限制序列表征。
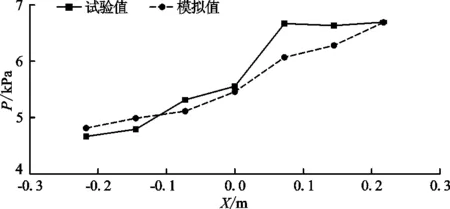
图7 消力井底板时均压强计算值与试验值对比
进而令α、β为位于同一涡旋流线上的两点,由流线定义分别求得与刚体转动分布不同的各点椭圆涡流速vα=-ma,vβ=mn2b(m、n为解参数),假设主流与涡旋衔接速度一致为um(m),令Pmean(kPa)为涡旋周围主流平均压强,则沿短轴bn(y′轴)面建立动量方程并积分得出:
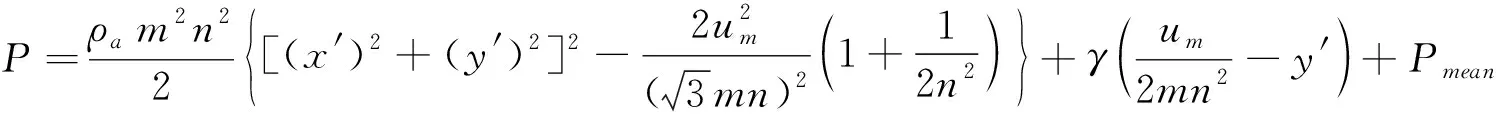
(11)
式中:γ为流场紊动水容重,N/m3。
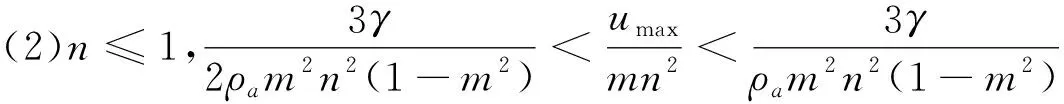
综上所述,井内水体压强可分解为水平轴对称及竖直变幅结构的有序特征叠加。
4 结 论
针对泄槽纵坡一定的条件下,尾水出口与泄槽轴线呈非对称正交的圆形消力井水力特性进行有限域数值模拟研究,在对比验证前期物理模型试验研究成果的基础上,进一步开展水流流态转换、流速分布和压强分布特性的机理分析,主要结论如下:
(1)消力井内水流流态在空间上沿射流方向依次呈平面横向紊动扩散自由射流、主流动力自相似淹没射流和冲击射流、近壁面附着扩散旋滚水跃3个临界雷诺数分区演变过程。
(2)消力井内射流沿程流速表现为以最大流速(射流水股在井内水体作用下产生一定弹射偏离)为顶切点的相似或自保持平面对称的等值曲线分布;射流厚度随周围流体的卷入而增加,其动量沿程衰减,断面流速分布趋于均匀。
(3)消力井内水体压强由紊动射流旋滚运动产生的附加压强和静水压强叠加而成,其有序结构特征可分解为水平归一化轴对称结构及竖直径向平均变幅结构两部分。

