宁波石栎-木荷天然常绿阔叶混交林的树高-胸径模型*

娄明华 白 超 杨同辉

(1. 宁波市农业科学研究院，浙江 宁波 315040; 2. 宁波市测绘和遥感技术研究院, 浙江 宁波 315042)

天然常绿阔叶混交林是宁波地区的典型地带性植被类型，具有结构复杂、生产力高、生物多样性丰富等特性，也是我国亚热带地区代表性的植被类型。可见，研究天然常绿阔叶混交林对宁波区域生态环境、碳平衡维护等方面起着重要作用[1-2]。树高与胸径是林业调查中的基本因子，是衡量林分结构和质量的重要指标[3]。树高数据对描述林分生长变化极其重要，其中优势高能直接反映树种当前环境立地质量的好坏，而林分平均高是林分蓄积量与生物量计算中不可或缺的变量[4]。在实践中，树高数据的获取相较于胸径难度更大，往往受林分密集度影响，在过密的林分由于观测视野受限，树高测量通常存在较大误差，故而往往先测定少数林木的树高，建立树高-胸径关系模型，再以胸径估计剩余林木的树高[5-8]。因此，构建准确的树高-胸径关系模型有重要的实际意义[6,9-10]。

目前已有大量关于人工林和天然林树高-胸径关系模型的研究。其中，天然林的研究以针叶林或针阔混交林为主，如冯国红等[11]以东北小兴安岭天然林针阔混交林为对象研究不同树种的树高-胸径关系模型；李善尧[12]以内蒙古樟子松Pinus sylvestris天然林为对象研究树高-胸径模型；郭嘉等[13]以陕西秦岭林区松栎林为对象研究树高-胸径模型；康波和寸永户[14]以云南4 种天然针叶林为对象研究树高-胸径模型；王冬至等[15]以华北落叶松Larix principis-rupprechtii与白桦Betula platyphylla混交林为对象研究树高-胸径关系模型等。

然而，宁波地区的天然常绿阔叶混交林树高-胸径关系模型研究未见报道。鉴于此，本文以宁波地区常见的石栎Lithocarpus glaber-木荷Schima superba天然常绿阔叶混交林为研究对象，建立适宜的树高-胸径模型，以期为宁波地区的天然常绿阔叶混交林的林木生长预测、森林经营管理、森林资源清查提供理论参考。

1 材料与方法

1.1 数据收集与统计

数据来源于宁波市2019 年调查的两个石栎-木荷天然常绿阔叶混交林固定样地，样地大小均为20 m×20 m。样地内，对树高≥1.5 m 的林木进行每木调查，记录树种，测量胸径、树高、枝下高、林木坐标等特征因子。为建模需要，将一个样地作为建模数据，另一个样地作为检验数据。建模数据与检验数据的基本统计量见表1。建模数据与检验数据的胸径与树高散点图，见图1。

图1 胸径与树高关系散点图Fig. 1 Scatter diagram of height against diameter at breast height

表1 建模与检验数据统计量(均值±标准差)Tab. 1 Summary statistics for calibration and validation data (mean±standard deviation)

1.2 建模方法

本文选用以下30 个常用的树高-胸径经验模型[6,9]（表2），通过比较分析寻找适宜的石栎-木荷天然常绿阔叶混交林的树高-胸径模型，并利用R 统计语言[16]进行建模及参数检验。

1.3 模型评价指标

本文选用了5 个指标[17]，分别为调整决定系数（adjusted coefficient of determination,Ra2）、均方根误差（root mean square error, RMSE）、平均绝对误差（mean absolute error, MAE）、相对平均绝对误差（relative mean absolute error, RMAE）和Akaike信息准则（Akaike information criterion, AIC），见表3。 其 中，Ra2、RMSE、MAE、RMAE 和AIC用于建模评价，RMSE、MAE 和RMAE 用于检验评价。

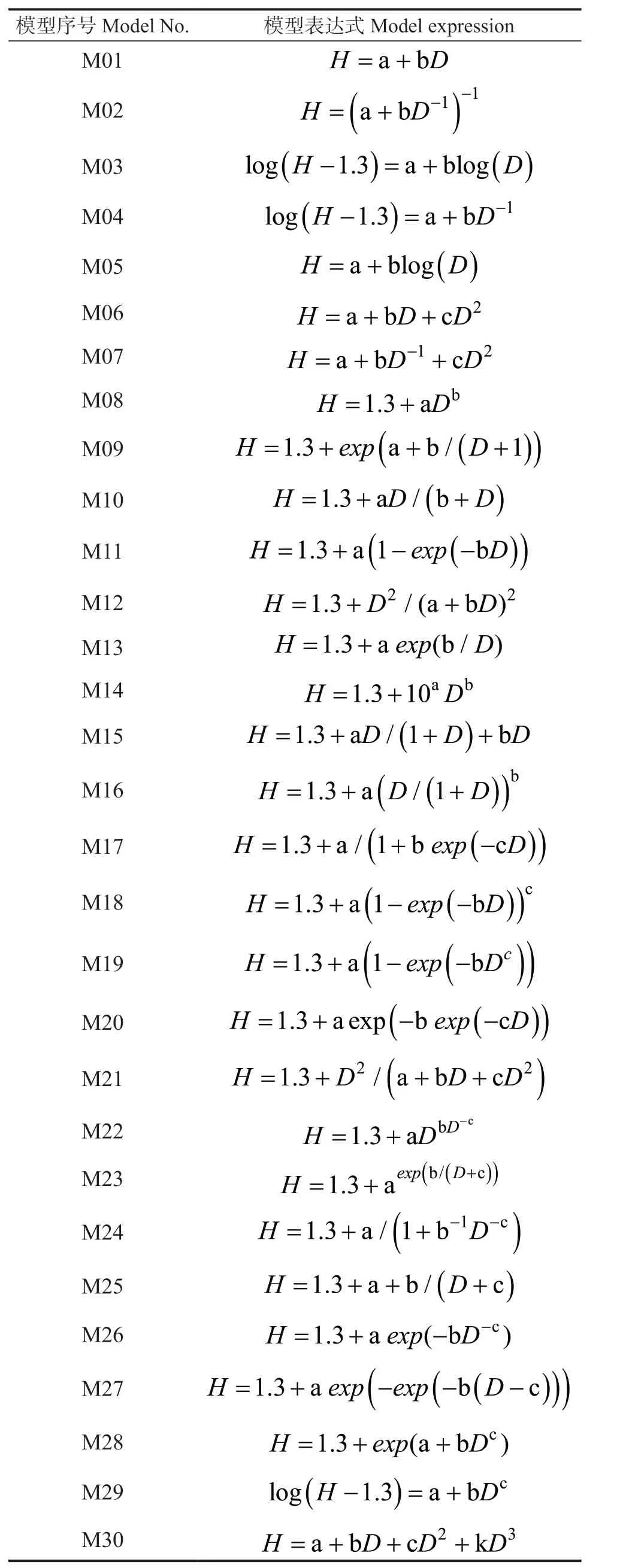
表 2 树高-胸径模型Tab. 2 Height-diameter models

表3 5 个模型评价指标Tab. 3 Five model evaluation indices

2 结果与分析

利用R 统计语言求解30 个模型，发现M23无法求解，其他29 个模型均能求解。29 个模型的拟合效果和参数估计，分别见表4、表5 和表6。

建模数据的拟合效果分析：由表4 和表5 可看出，Ra2的平均值为0.890 4，M19 具有最大Ra2值为0.921 7。Ra2值小于0.8 的有2 个即M07和M01，其Ra2值分别为0.728 2 和0.758 2。其中Ra2值大于0.91 的有15 个模型，该15 个模型按Ra2值由大到小排序，其对应的模型为：M19、M20、M27、M18、M24、M17、M06、M21、M22、M09、M16、M12、M26、M28、M29。 与此同时，该15 个模型的AIC 值和建模数据的RMSE 值由小到大排序的顺序，均与其Ra2值由大到小排序的顺序相同，AIC 值的范围为679.139 9至965.276 8，建模数据的RMSE 值的范围为1.050 0 至1.955 9；建模数据的MAE 值，其范围为0.754 2 至1.563 7，由小到大排序的前15 个模型依次为：M20、M27、M19、M18、M06、M24、M17、M21、M22、M09、M16、M12、M26、M28、M29；建模数据的RMAE 值，其范围为0.138 1 至0.265 7，由小到大排序的前15 个模型依 次 为：M20、M27、M06、M19、M18、M09、M12、M24、M17、M21、M11、M02、M10、M16、M22。

检验数据的拟合效果分析：由表4 和表5 可看出，检验数据的RMSE 值，其范围为1.346 1至1.813 8，由小到大排序的前15 个模型依次为：M15、M03、M08、M14、M01、M10、M30、M11、M07、M02、M25、M12、M05、M09、M26；检验数据的MAE 值，其范围为1.040 5 至1.415 1，由小到大排序的前15 个模型依次为：M03、M08、M14、M15、M01、M10、M02、M30、M25、M11、M12、M05、M09、M26、M28；检验数据的RMAE 值，其范围为0.143 0至0.438 2，由小到大排序的前15 个模型依次为：M07、M12、M09、M02、M25、M10、M03、M08、M14、M16、M26、M28、M29、M11、M24。

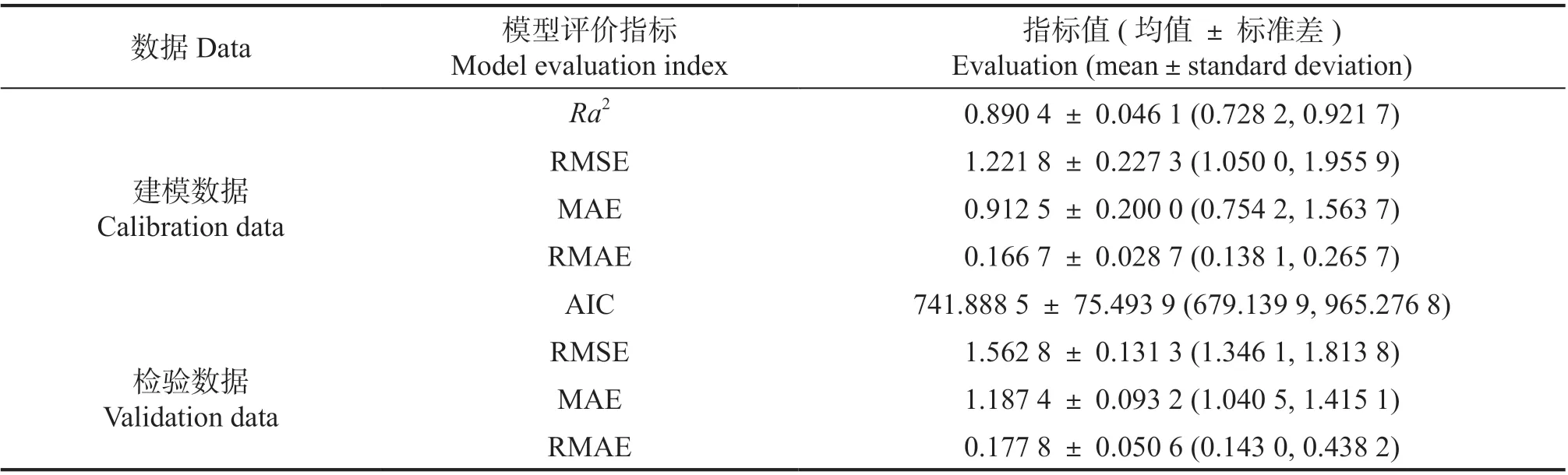
表5 29 个模型的模型评价指标值Tab. 5 Model evaluation for 29 models

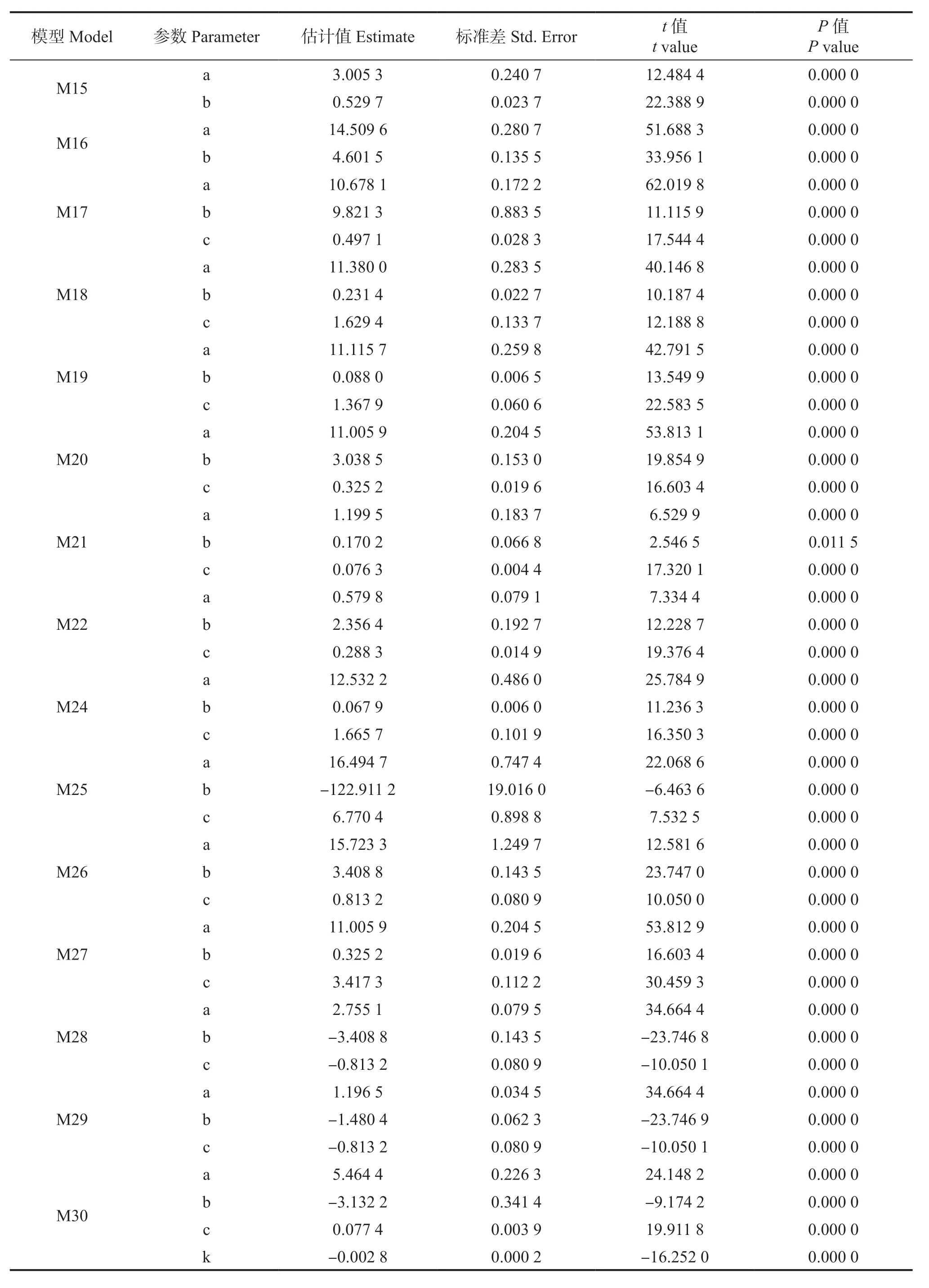
参数检验分析：由表6 可看出，M21 中参数b 的P值为0.011 5，介于0.05 与0.01 之间，说明有显著统计学差异。除M21，其余28 个模型的参数P值均小于0.000 1，说明有极显著统计学差异。

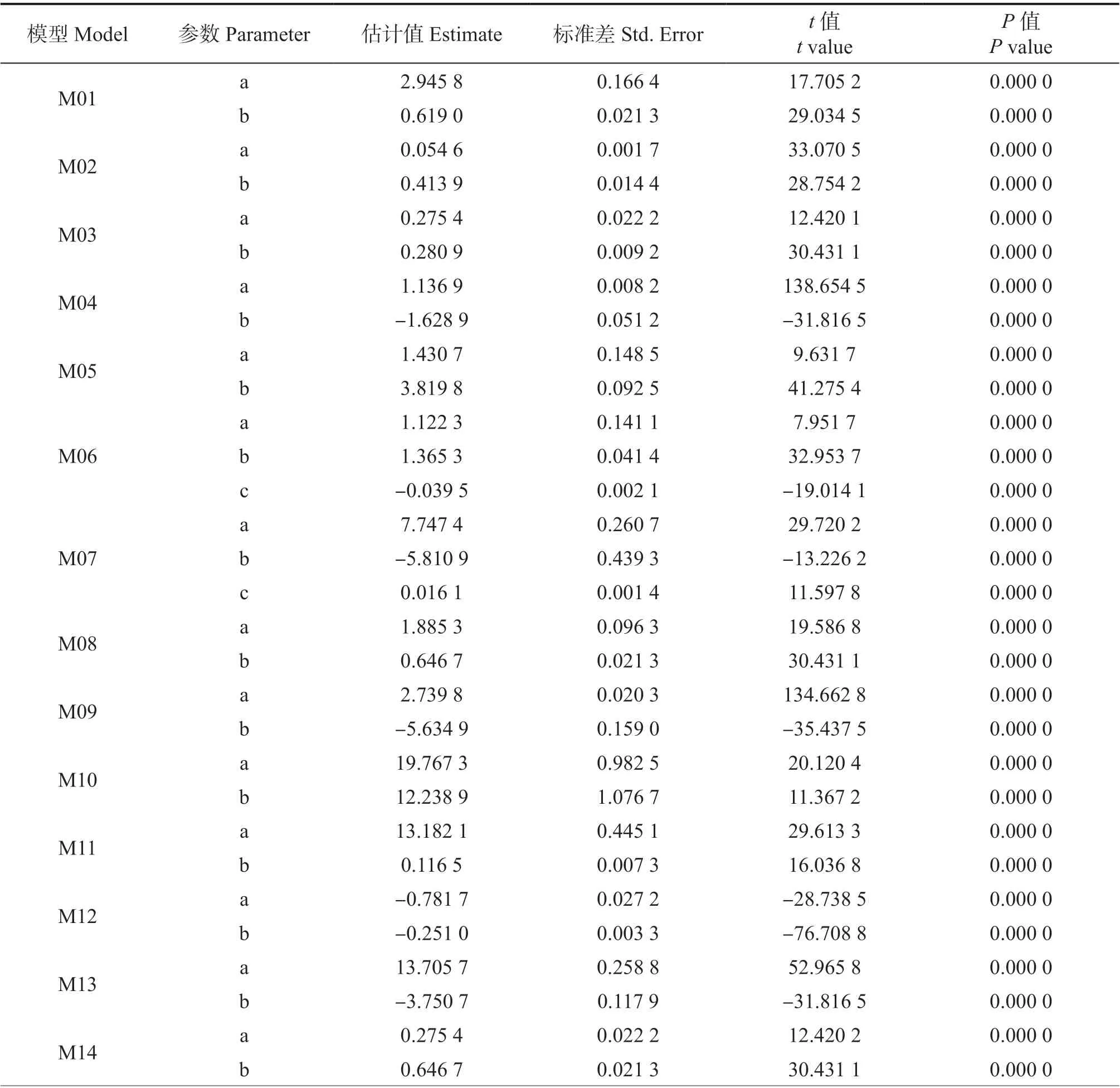
表6 29 个模型参数估计Tab. 6 Parameter estimates for 29 models

比较分析上述的建模数据的Ra2、RMSE、MAE、RMAE 和AIC 和 检 验 数 据 的RMSE、MAE、RMAE 的前15 个模型，发现M09、M12 和M26均出现在前15 个模型中，说明这3 个模型是较优模型，见表7。

从表7 可知，建模数据中，M09 的5 个评价指标最优，其次为M12，第三为M26；检验数据中，M12 的3 个评价指标最优，其次为M09，第三为M26。结合考虑建模数据和检验数据的评价指标，M09 和M12 均为适宜的树高-胸径模型，M09 和M12 的模型拟合曲线，见图2。若侧重考虑建模数据的拟合效果，则推荐选用M09；若侧重考虑检验数据的拟合效果，则推荐选用M12。

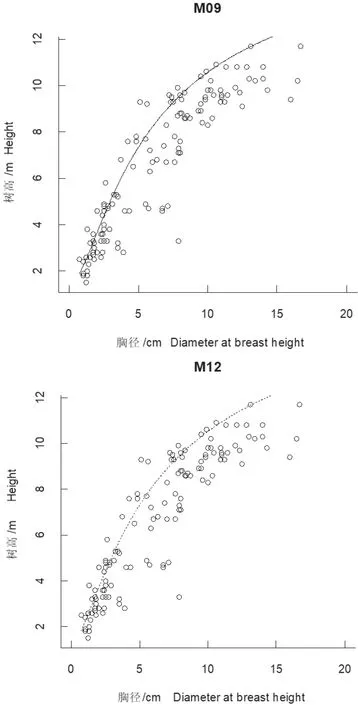
图2 检验数据的模型拟合曲线Fig. 2 Model fitting curve for validation data

表7 3 个较优模型的拟合效果Tab. 7 Fitting performance for 3 better models

模型Model 参数Parameter 估计值Estimate 标准差Std. Error t 值t value P 值P value M15 a 3.005 3 0.240 7 12.484 4 0.000 0 b 0.529 7 0.023 7 22.388 9 0.000 0 M16 a 14.509 6 0.280 7 51.688 3 0.000 0 b 4.601 5 0.135 5 33.956 1 0.000 0 M17 M18 M19 M20 M21 M22 M24 M25 M26 M27 M28 M29 10.678 1 0.172 2 62.019 8 0.000 0 b 9.821 3 0.883 5 11.115 9 0.000 0 c 0.497 1 0.028 3 17.544 4 0.000 0 a 11.380 0 0.283 5 40.146 8 0.000 0 b 0.231 4 0.022 7 10.187 4 0.000 0 c 1.629 4 0.133 7 12.188 8 0.000 0 a 11.115 7 0.259 8 42.791 5 0.000 0 b 0.088 0 0.006 5 13.549 9 0.000 0 c 1.367 9 0.060 6 22.583 5 0.000 0 a 11.005 9 0.204 5 53.813 1 0.000 0 b 3.038 5 0.153 0 19.854 9 0.000 0 c 0.325 2 0.019 6 16.603 4 0.000 0 a 1.199 5 0.183 7 6.529 9 0.000 0 b 0.170 2 0.066 8 2.546 5 0.011 5 c 0.076 3 0.004 4 17.320 1 0.000 0 a 0.579 8 0.079 1 7.334 4 0.000 0 b 2.356 4 0.192 7 12.228 7 0.000 0 c 0.288 3 0.014 9 19.376 4 0.000 0 a 12.532 2 0.486 0 25.784 9 0.000 0 b 0.067 9 0.006 0 11.236 3 0.000 0 c 1.665 7 0.101 9 16.350 3 0.000 0 a 16.494 7 0.747 4 22.068 6 0.000 0 b-122.911 2 19.016 0 -6.463 6 0.000 0 c 6.770 4 0.898 8 7.532 5 0.000 0 a 15.723 3 1.249 7 12.581 6 0.000 0 b 3.408 8 0.143 5 23.747 0 0.000 0 c 0.813 2 0.080 9 10.050 0 0.000 0 a 11.005 9 0.204 5 53.812 9 0.000 0 b 0.325 2 0.019 6 16.603 4 0.000 0 c 3.417 3 0.112 2 30.459 3 0.000 0 a 2.755 1 0.079 5 34.664 4 0.000 0 b-3.408 8 0.143 5 -23.746 8 0.000 0 c-0.813 2 0.080 9 -10.050 1 0.000 0 a 1.196 5 0.034 5 34.664 4 0.000 0 b-1.480 4 0.062 3 -23.746 9 0.000 0 c-0.813 2 0.080 9 -10.050 1 0.000 0 a a M30 5.464 4 0.226 3 24.148 2 0.000 0 b-3.132 2 0.341 4 -9.174 2 0.000 0 c 0.077 4 0.003 9 19.911 8 0.000 0 k-0.002 8 0.000 2 -16.252 0 0.000 0

3 结论与讨论

为选择适宜的石栎-木荷天然常绿阔叶混交林树 高-胸径模型，本文选用30 个常用的树高-胸径经验模型，建立了29 个模型（M23 无法求解），并利用5 个模型评价指标比较分析了29 个模型的拟合效果。综合考虑建模数据和检验数据的模型评价指标和参数检验，可得出以下结论：

（1）M09 和M12 可作为适宜的石栎-木荷天然常绿阔叶混交林树高-胸径模型，公式如下：

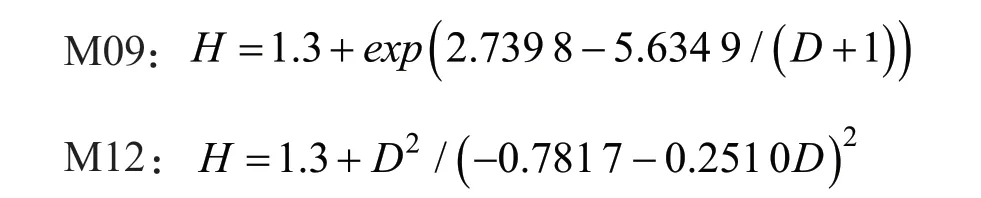
（2）若侧重考虑建模数据的拟合效果，则推荐选用M09，其Ra2=0.914 1；若侧重考虑检验数据的拟合效果，则推荐选用M12，其Ra2=0.912 6。

本文建立了适宜的石栎-木荷天然常绿阔叶混交林树高-胸径模型，可为后续研究相关的森林资源信息系统[18-19]、森林遥感分析[20-22]等方面提供基础理论模型。

卢军等[9]以长白山地区的云冷杉Picea asperata、Akjes fabri针阔混交林的幼树树高≥1.3 m且1.0 cm ≤胸径＜5.0 cm 的林木研究对象，探索比较分析适宜的幼树树高-胸径模型，研究认为M30 是最适宜的模型，这与本文结论不一致即M09 和M12 可作为适宜的石栎-木荷常绿阔叶混交林树高-胸径模型。分析不一致原因，可能是研究对象不同所致，本文研究对象为宁波地区的石栎-木荷天然常绿阔叶混交林，林木胸径范围为0.5～25.5 cm，进一步说明了模型适宜性可能与林分类型（树种）、林木胸径范围、研究地区（如气候、经纬度等地区差异）等因素有关，考虑这些因素的树高-胸径模型是下一步值得研究的问题。

由于建模样本数据有限，本文研究对象的树高1.5 m 以上的林木，其胸径范围为0.5～25.5 cm，通过模型比较分析得出M09 和M12 可作为适宜宁波地区的石栎-木荷天然常绿阔叶混交林树高-胸径模型，说明M09 与M12 目前仅针对林木胸径范围为0.5～25.5 cm 的林木预测树高。因此，为增加石栎-木荷天然常绿阔叶混交林树高-胸径模型的林木胸径适用范围，可扩大建模样本的林木胸径范围，如胸径范围扩大至60、80 cm 等，比较分析不同林木胸径范围下的树高-胸径模型，这是下一步值得研究的问题。