基于自组织映射网络和遗传算法优化Elman神经网络的全网短期负荷预测模型

郑云飞， 赵红生， 王博， 潘笑， 潘兴亚

(1. 国网湖北省电力有限公司经济技术研究院，湖北 武汉 430077；2. 国网湖北省电力有限公司，湖北 武汉 430077；3. 武汉大学 电气与自动化学院，湖北 武汉 430072)

0 引 言

电能无法大量储存，因此在发电厂运行以及电能调度的过程中，要求发电厂出力与系统负荷的波动保持动态平衡。对电力负荷进行精准预测不仅可以提高电网运行的可靠性与经济性，而且影响着配电网的科学规划与发展[1-2]。因此如何提高全网短期负荷的预测精度成为配电网运行与规划的关键技术。

为了提升负荷预测结果的可信度及可观测性，负荷聚类算法在短期负荷预测领域得到了广泛的应用。文献[3]对历史负荷数据进行分析，基于不同聚类算法寻找最优的典型日负荷曲线。文献[4]利用聚类模型对负荷信息进行特征提取，寻找与预测日相似的历史数据作为预测样本，可以有效地提升预测精度和速度。然而上述方法直接对全网负荷进行预测，无法实现在负荷预测过程中的可视化。文献[5-6]基于不同的负荷数据的特征参量集合，对相应的聚类算法进行改进，对不同用电习惯的用户终端进行分类，得到更为精细化的分类结果。

上述方法主要集中于对短期负荷预测模型精度和速度的改进，无法通过负荷曲线提取用户的用电习惯，阻碍了售电侧对信息的理解。针对上述方法的缺陷，本文首先考虑不同的用电习惯，利用自组织映射网络(self-organizing feature map，SOM)实现负荷分类，然后利用遗传算法(genetic algorithm，GA)优化的Elman神经网络对全网负荷进行差异化预测，最后基于负荷综合稳定度得到全网负荷预测结果。本文提出的SOM-GA-Elman模型不仅可以有效提升全网短期负荷预测的精度，而且适用于部分子网数据缺失的情况，为电网负荷的精细化管理提供参考。

1 基于SOM-GA-Elman的全网短期负荷预测模型

1.1 通过SOM聚类划分子网

电网负荷是量大、高维和多数据类型混杂的大数据集，这一特点使得从电网数据中挖掘出不同类型的负荷特性成为一个难点。本文通过SOM网络实现电网负荷数据的降维处理并将其投影到二维空间，将复杂的电网数据进行简化以实现可视化，从而获得不同类型的用户用电习惯。二维SOM网络的结构如图1所示。

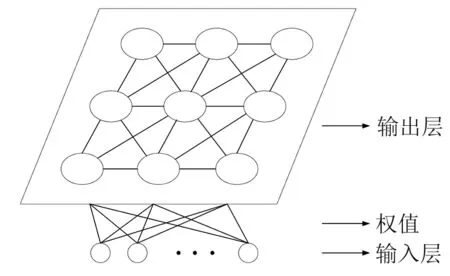
图1 二维SOM网络的结构图

由图1可知：二维SOM网络由输入层和输出层(竞争层)连接构成，网络的输出层神经元与邻域其他神经元之间广泛相连，可以实现两者的相互激励，输入神经元与输出神经元则基于权向量实现两者的全连接。基于SOM聚类方法对电网负荷历史数据进行分析，将具有相似负荷特性的终端进行聚类，获得具有不同负荷特性的子网系统。

1.2 利用GA-Elman神经网络预测子网负荷

Elman神经网络在负荷预测领域具有广泛的应用[7]。本文在利用Elman 神经网络对各子网负荷分别进行预测时，引入GA对网络的权重以及阈值进行差异性优化，克服了寻优过程中的盲目性，同时避免出现局部收敛现象，从而大幅改善网络的寻优性能。本文提出的GA-Elman预测模型如图2所示。

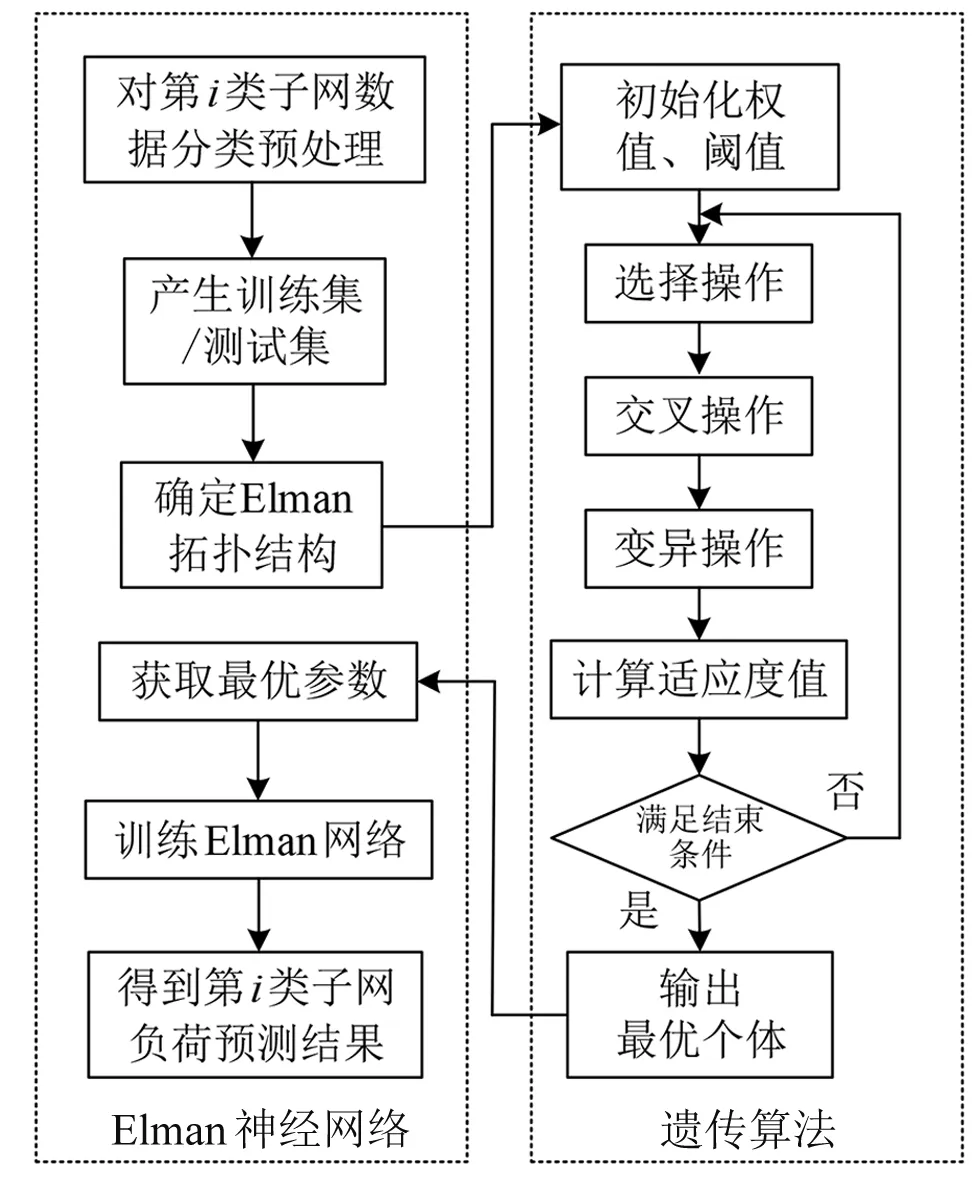
图2 GA-Elman预测模型

1.3 基于负荷综合稳定度得到全网预测值

目前，针对全网短期负荷的预测需求，常见的方法是首先对负荷特性进行聚类分析，将全网划分为多个子网，然后对各个子网的负荷分别进行预测，再将各个子网的负荷预测结果直接进行累加求和，最终得到全网负荷预测结果。但由于各个子网的负荷波动程度差异较大，预测的难度各不相同，上述的“子网累加法”需要获得所有子网的预测结果，对于缺少一个或几个子网预测值的情况无能为力。

各子网的实时负荷占比在每个时间节点是大致稳定的，因此全网负荷预测值可用式(1)表示。

(1)

式中：load(i,t)为第i个子网在t时刻点的负荷预测结果，由Elman神经网络模型预测得出；P(i,t)为第i个子网在t时刻点的负荷占比，可取历史数据的平均值；L(i,t)为第i个子网在t时刻点的全网系统负荷预测结果。

由式(1)可知，每个子网负荷预测值都可以映射获得一个相应的全网负荷预测值。由于各子网负荷占全网负荷的比例不同，各子网的稳定性在预测全网负荷时的影响程度也不同，为了衡量子网负荷的稳定性，引入负荷综合稳定度指标STA。

(2)

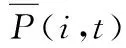
为了避免极端误差的出现，一般挑选STA指标较小的r个子网来获得较为准确的全网负荷。设这r个子网分别为1,2,…,r，则t时刻点的全网负荷预测结果可表示为：

(3)

式中:α(i,t)为由第i个子网映射得到的全网负荷预测值在t时刻的权重。

为了得到各个子网的权重矩阵，本文以历史样本空间内t时刻点的预测残差平方和最小为目标，构建如下非线性优化模型。

(4)

式中:n为历史样本的天数；L(i,t,j)为第j天t时刻由第i个子网映射出的全网负荷预测值；Lreal(t,j)为第j天t时刻的实际全网负荷结果。

求解上述优化问题，求解各个时刻点的权重系数值后，即可根据式(3)获得预测日各时刻点的全网负荷预测结果。

为了对全网负荷预测结果的精准程度进行量化分析，本文采用预测结果的均方根误差(mean square error, MSE)对预测模型的精度进行表征。计算公式如式(5)所示。

(5)

2 算例分析

2.1 数据预处理

本文提取某市电网系统中专变用户的负荷有功功率作为测试数据集，数据集中包含743个样本数据。智能电表以15 min为间隔对负荷有功功率进行采样，得到采样频率为96点/d的负荷曲线。通过用户用电信息采集系统提取2019年10月10日—10月29日的用户日负荷曲线。

2.1.1 负荷数据预处理

本文以日有功功率最大值为基准对用户日负荷曲线数据进行预处理，主要包括空缺值填充、异常值剔除和数据归一化，具体过程本文不再赘述。为了更直观地对负荷数据进行分析，本文选取了5个特征指标。

(1)日平均负荷：预测日内全部负荷点的平均值。

(2)日负荷率=日平均负荷/日最大负荷。

(3)峰时耗电率=高峰时段负荷量/待预测日总负荷量。

(4)日峰谷差率=日峰谷差/日最大负荷。

(5)平段的用电量百分比。

2.1.2 非负荷样本数据预处理

在对各子网负荷进行预测时，还需要综合考虑天气和节假日等影响因素对负荷变化的影响。对当地温度以及湿度进行等时刻采样，可以得到天气数据集，同时还需要对节假日信息进行关联分析。影响因素的具体指标如表1所示。

表1 非负荷样本的影响指标

2.2 SOM可视化聚类

本文选取2.1.1节中的5个特征指标建立短期负荷的聚类模型。为了易于理解聚类所要传递的信息，一般设置竞争层的节点数略大于输入样本的个数，本文将SOM网络竞争层节点数设定为12×12，将最大迭代次数设置为100，从而保证得到的聚类结果具有较好的收敛效果。图3是网络聚簇分布图。观察该图可知，有四簇颜色较浅，代表每簇节点距离较近，每簇间都有较深的颜色节点将其分开，故该数据集聚为四类。神经元分类情况如图4所示，深色正方形表示胜利的神经元，其中数字“n”表示有n个输入神经元被相应竞争层神经元激发，白色表示没有神经元被激发，相同的数字代表被聚为一类，总体被聚为四簇。

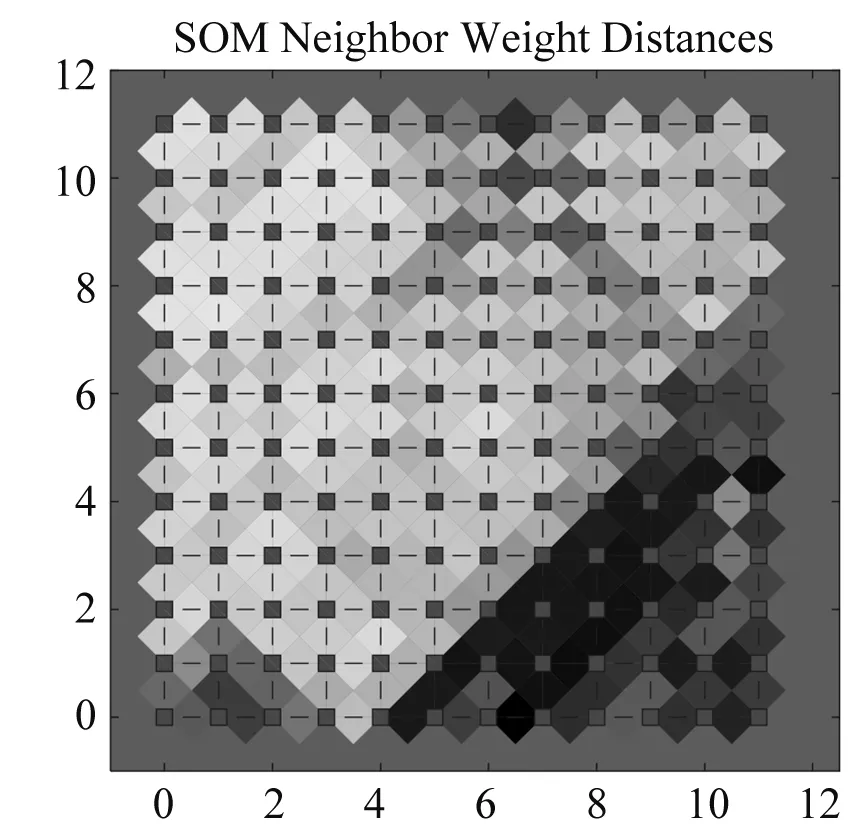
图3 聚簇分布特征图

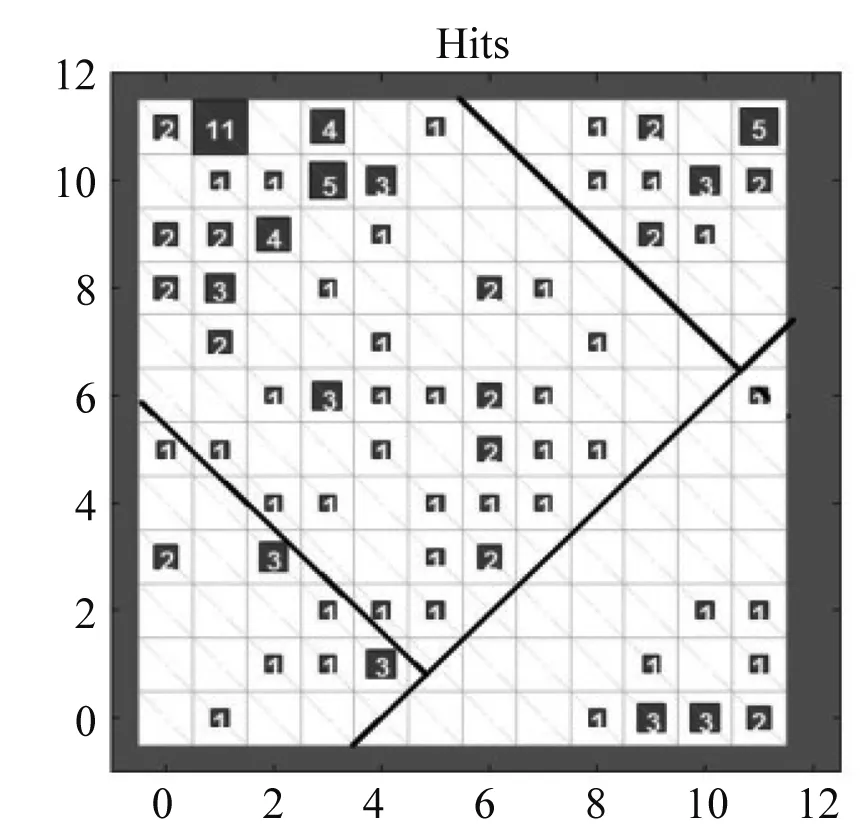
图4 神经元分类情况

2.3 GA-Elman神经网络负荷预测

本文以2019年10月10日—10月29日的预处理数据作为训练样本，每7 d的负荷及天气、节假日数据作为输入向量，第8 d的负荷作为目标向量，从而得到13组训练样本，以10月30日的负荷数据作为网络的测试样本。

本文采用GA-Elman对各类子网的负荷分别进行预测，迭代次数设为500次，迭代目标设为0.01，适应度函数为MSE。遗传算法初始种群数设为500，交叉概率设为0.4，变异概率设为0.1，遗传代数设为100代。预测结果如图5～图8所示。

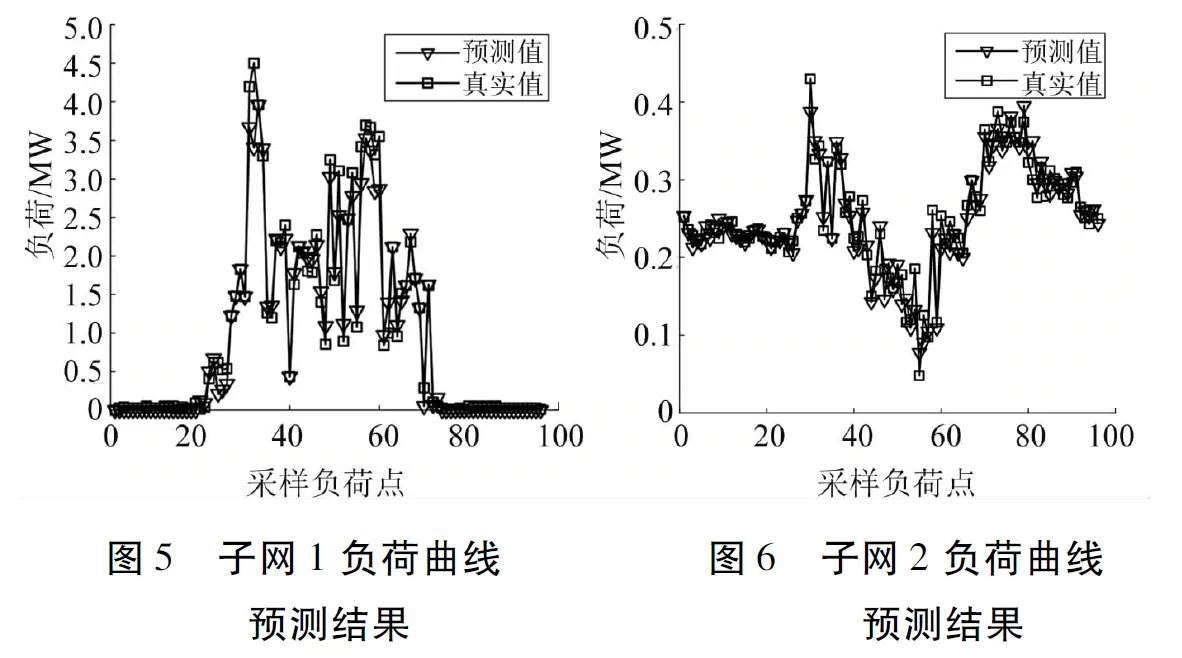
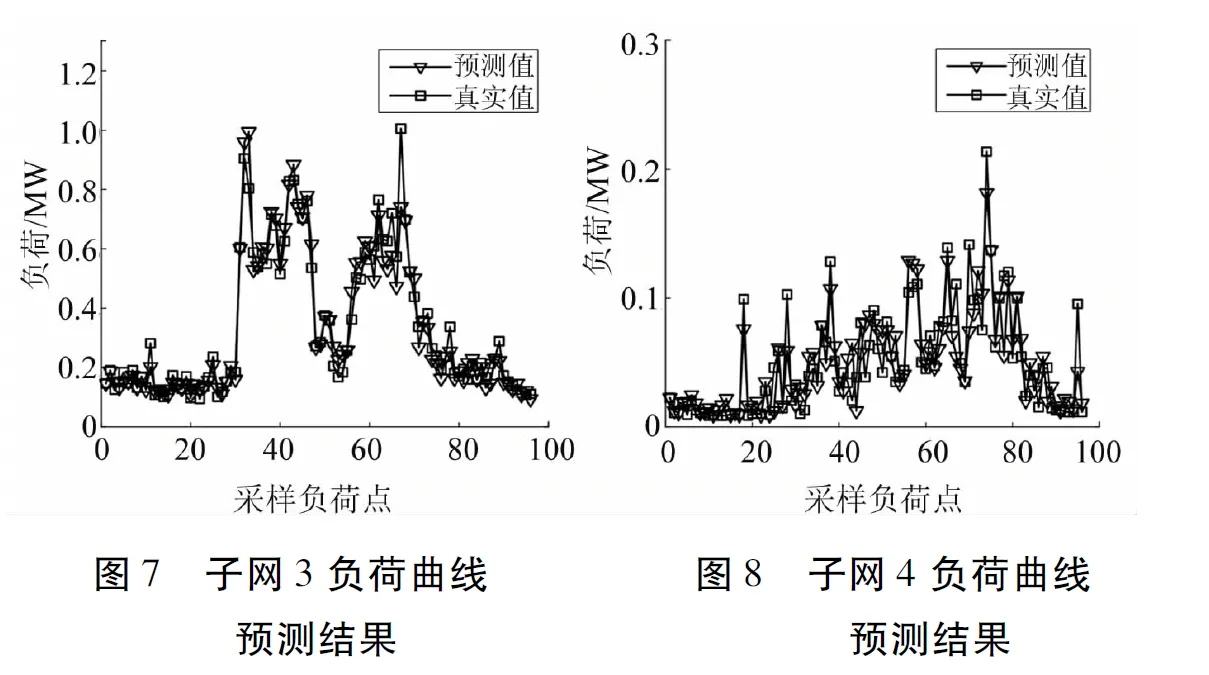
为了验证GA-Elman模型对各子网负荷的预测精度，本文基于传统的Elman神经网络对各子网负荷进行预测。将预测结果进行对比，如表2所示。

由表2可知，相比于传统的Elman神经网络，本文采用的GA-Elman具有更好的适用性，对各个子网均具有更高的预测精度。

2.4 全网预测结果

将本文方法与传统的“子网累加法”的预测结果进行对比，通过对式(5)中的MSE进行分析计算，得到如图9所示的预测误差曲线。

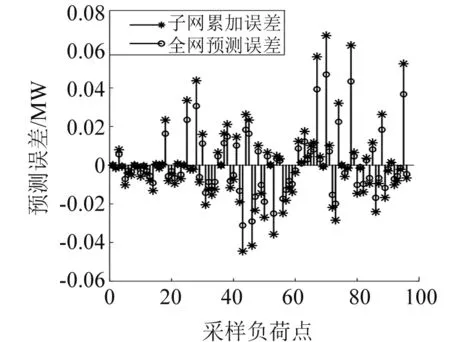
图9 预测结果对比

由图9可知，相比于常见的"子网累加法"，基于子网负荷综合稳定度得到的预测结果具有更高的精确度。本文提出的全网负荷模型不仅能够提高负荷预测的精度，而且预测过程不依赖全部负荷数据，适用于存在数据缺失的配网负荷预测，具有较强的适用性。

3 结束语

本文提出了一种基于SOM-GA-Elman的全网短期负荷预测模型，该模型能够尽可能地保留负荷数据的潜在特征，得到不同特性的负荷曲线，有利于分析用户用电习惯，从而提高预测精度。对实际算例的分析证明了该集成预测方法具有较高的预测精度。该预测模型同样适用于部分子网数据缺失而需要得到全网结果的情况，在实际电网规划应用中，具有较强的适用性，满足智能配电网发展的内在要求。